math_review
topics
mathmatics
- supreme and optimum
- Norm and Linear product
- topology of R*
- Continuious Function
supreme and optimum
Def 1: 非空有界集合必有上确界
common norm
(1) x ∈ \in ∈ Rn, ||x||2= x 1 2 + x 2 2 + . . . + x n 2 \sqrt {x_1^2+x_2^2+...+x_n^2} x12+x22+...+xn2
(2) x ∈ \in ∈ R
Norm of vector
Def 2: a function f : Rn → \rightarrow → R is called norm,if
(1) f(x)>=0 & f(x)=0 if x= 0 ⃗ \vec 0 0
(2) homogenous: f(tx)=|t| f(x)
(3) triangle inquality: f(x+y)<=f(x)+f(y)
f(x)=||x||k
common norm
(1) x ∈ \in ∈ Rn, ||x||2= x 1 2 + x 2 2 + . . . + x n 2 \sqrt {x_1^2+x_2^2+...+x_n^2} x12+x22+...+xn2
(2) x ∈ R n \in\ R^n ∈ Rn, ∣ ∣ x ∣ ∣ p = ( x 1 p + . . . + x n p ) 1 p ||x||_p=(x_1^p+...+x_n^p)^{\frac 1 p} ∣∣x∣∣p=(x1p+...+xnp)p1
(2) xKaTeX parse error: Got function '\inf' with no arguments as subscript at position 15: \in R^n,||x||_\̲i̲n̲f̲=max\{|x_1|,...…
Def 3: Unit Ball
B = x ∈ R n , ∣ ∣ x ∣ ∣ ≤ 1 B={x\in R^n,||x||\leq 1} B=x∈Rn,∣∣x∣∣≤1
norm of matrix
P ∈ S + + n , ∣ ∣ x ∣ ∣ p = ( < x , P x > ) 1 2 P\in S_{++}^n,||x||_p=(<x,P_x>)^\frac 1 2 P∈S++n,∣∣x∣∣p=(<x,Px>)21
- KaTeX parse error: Got function '\sum' with no arguments as argument to '\sqrt' at position 15: ||A||_F=\sqrt \̲s̲u̲m̲_{i=1}^m\sum_{j…
- ∣ ∣ A ∣ ∣ p = m a x ∣ ∣ x ∣ ∣ p = 1 ∣ ∣ A x ∣ ∣ p ||A||_p=\underset {||x||_p=1}{max}||Ax||_p ∣∣A∣∣p=∣∣x∣∣p=1max∣∣Ax∣∣p
- ∣ ∣ A ∣ ∣ = m a x j ∑ i ∣ a i j ∣ ||A||=\underset j {max} \sum_i |aij| ∣∣A∣∣=jmax∑i∣aij∣
- ∣ ∣ A ∣ ∣ 2 = σ ( A ) ||A||_2=\sigma(A) ∣∣A∣∣2=σ(A)(奇异值,特征值绝对值最大)
- KaTeX parse error: Got function '\inf' with no arguments as subscript at position 7: ||A||_\̲i̲n̲f̲=\underset i{ma…
Inner product
f: R n ⊙ R n → R R^n \odot R^n \rightarrow R Rn⊙Rn→R
- Nonnegative: f ( x , x ) ≥ 0 , f ( x , x ) = 0 i f f x = 0 f(x,x)\geq 0,f(x,x)=0 iff x=0 f(x,x)≥0,f(x,x)=0iffx=0
- Symmetric: f ( x , y ) = f ( y , x ) f(x,y)=f(y,x) f(x,y)=f(y,x)
- Bilinear: f ( a x + b y , z ) = a f ( x , z ) + b f ( y , z ) f(ax+by,z)=af(x,z)+bf(y,z) f(ax+by,z)=af(x,z)+bf(y,z)
f ( z , a x + b y ) = a f ( z , x ) + b f ( z , y ) f(z,ax+by)=af(z,x)+bf(z,y) f(z,ax+by)=af(z,x)+bf(z,y)
f(x,y)=<x,y>
定义了内积of vector,we can find corresponding norm;法
< x , x > = ∣ ∣ x ∣ ∣ 2 2 <x,x>=||x||_2^2 <x,x>=∣∣x∣∣22, < x , x > p = ∣ ∣ x ∣ ∣ p 2 <x,x>_p=||x||_p^2 <x,x>p=∣∣x∣∣p2
given norm ,we can’t find corresponding inner product always(like KaTeX parse error: Got function '\inf' with no arguments as subscript at position 7: ||x||_\̲i̲n̲f̲)
example of inner product
- comply with above 3 properties
- A , B ∈ R m + n , < A , B > = t r ( A T B ) = ∑ i j a i j b i j A,B\in R^{m+n},<A,B>=tr(A^TB)=\sum_{ij}a_{ij} b_{ij} A,B∈Rm+n,<A,B>=tr(ATB)=∑ijaijbij
- l 2 ( R ) = x = ( x 1 , . . . ) , x 1 ∈ R , ∑ i = 1 n ∣ x ∣ 2 < inf l^2(R)={x=(x_1,...),x_1\in R,\sum_{i=1}^n |x|^2<\inf} l2(R)=x=(x1,...),x1∈R,∑i=1n∣x∣2<inf
KaTeX parse error: Got function '\inf' with no arguments as superscript at position 18: …,y>=\sum_{i=1}^\̲i̲n̲f̲ ̲x_iy_i < \inf - L 2 ( R ) = f : R → R , ∫ R ∣ f ( x ) ∣ 2 d x < inf L^2(R)={f:R\rightarrow R,\int_R|f(x)|^2 dx<\inf} L2(R)=f:R→R,∫R∣f(x)∣2dx<inf
< f , g > L 2 = ∫ R f ( x ) g ( x ) d x <f,g>_{L^2}=\int_Rf(x)g(x)dx <f,g>L2=∫Rf(x)g(x)dx
Def 5: x , y ∈ R n x,y \in R^n x,y∈Rn
included angle, a n g ( x , y ) = a r c c o s < x , y > ∣ ∣ x ∣ ∣ ∣ . ∣ ∣ y ∣ ∣ ang(x,y)=arccos \frac {<x,y>}{||x|||.||y||} ang(x,y)=arccos∣∣x∣∣∣.∣∣y∣∣<x,y>
Topology of IRn
logistic chain: N o r m → U n i t B a l l → N e i g h b o u r h o o d → L i m i t Norm\rightarrow Unit Ball\rightarrow Neighbourhood\rightarrow Limit Norm→UnitBall→Neighbourhood→Limit
Def 6: given ϵ \epsilon ϵ,the ϵ \epsilon ϵ-neighbourhood of a point x
N ϵ ( x ) = y , y ∈ I R n , ∣ ∣ y − x ∣ ∣ < ϵ N_{\epsilon}(x)={y,y\in IR^n,||y-x||<\epsilon} Nϵ(x)=y,y∈IRn,∣∣y−x∣∣<ϵ
Def 7: interor point of S, ∃ ϵ > 0 , N ϵ ( x ) ∈ S \exists \epsilon>0,N_{\epsilon}(x)\in S ∃ϵ>0,Nϵ(x)∈S
Def 8: interior of S,the set of all interior points of S
Def 9: Open set O=int O
Def 10: Closed Set IR\F is open
Def 11: ( x k ) (x_k) (xk) converges to x,if ∀ ϵ > 0 , ∀ p , ∣ ∣ x k − x ∣ ∣ p < ϵ , i f k > N \forall \epsilon>0,\forall p,||x_k-x||_p<\epsilon,if\ k>N ∀ϵ>0,∀p,∣∣xk−x∣∣p<ϵ,if k>N
Def 12:(limited point) x ∈ I R n , S ∈ I R n , ∃ ( x k ) , x k ≠ x , ( x k ) ∈ S , s . t . x k → x x\in IR^n,S\in IR^n,\exists (x_k),x_k\neq x,(x_k)\in S,s.t. x_k\rightarrow x x∈IRn,S∈IRn,∃(xk),xk=x,(xk)∈S,s.t.xk→x
Def 13: F is closed if it c ontains all its limit points
相关文章:

math_review
topics mathmatics supreme and optimumNorm and Linear producttopology of R*Continuious Function supreme and optimum Def 1: 非空有界集合必有上确界 common norm (1) x ∈ \in ∈ Rn, ||x||2 x 1 2 x 2 2 . . . x n 2 \sqrt {x_1^2x_2^2...x_n^2} x12x22.…...
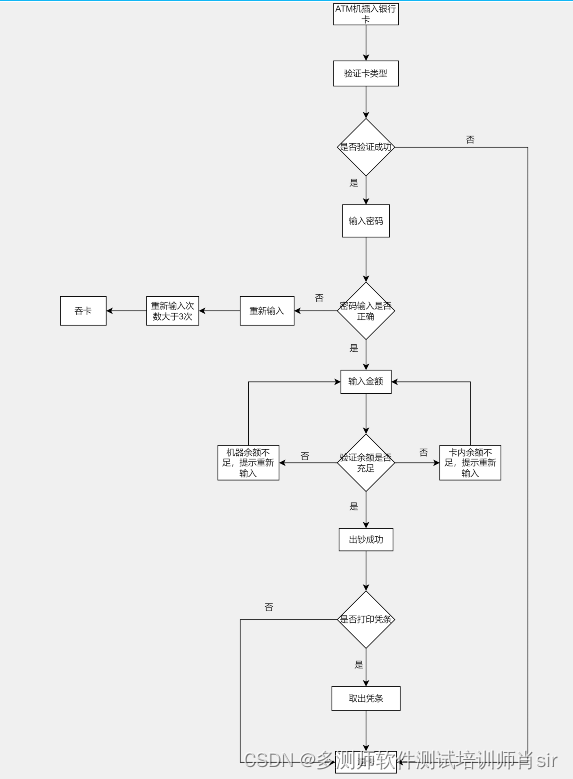
肖sir__设计测试用例方法之场景法04_(黑盒测试)
设计测试用例方法之场景法 1、场景法主要是针对测试场景类型的,顾也称场景流程分析法。 2、流程分析是将软件系统的某个流程看成路径,用路径分析的方法来设计测试用例。根据流程的顺序依次进行组合,使得流程的各个分支能走到。 举例说明&…...

plt函数显示图片 在图片上画边界框 边界框坐标转换
一.读取图片并显示图片 %matplotlib inline import torch from d2l import torch as d2l读取图片 image_path ../data/images/cat_dog_new.jpg # 创建画板 figure d2l.set_figsize() image d2l.plt.imread(image_path) d2l.plt.imshow(image);二.给出一个(x左上角,y左上角,…...

运行期获得文件名和行号
探索动态日志模块的实现 最初的目标是创建一个通用的日志模块, 它具有基本的日志输出功能并支持重定向. 这样, 如果需要更换日志模块, 可以轻松实现. 最初的构想是通过函数重定向, 即使用 dlsym 来重定向所有函数以实现打印功能. 然而, 这种方法引发了一个问题, 即无法正确获…...

数组操作UNIAPP
字符串转数组 let string "12345,56789" string.split(,) // [12345,56789] 数组转字符串 let array ["123","456"] array.join(",") // "123,456" 数组元素删除 let array [123,456] // 删除起始下标为1࿰…...
MySQL——无法打开MySQL8.0软件安装包或者安装过程中失败,如何解决?
在运行MySQL8.0软件安装包之前,用户需要确保系统中已经安装了.Net Framework相关软件,如果缺少此软件,将不能正常地安装MySQL8.0软件。 解决方案:到这个地址 https://www.microsoft.com/en-us/download/details.aspx?id42642…...

DB2存储过程如何编写和执行
db2执行文件参数: -t 表示语句使用默认的语句终结符——分号; -v 表示使用冗长模式,这样 DB2 会显示每一条正在执行命令的信息; -f 表示其后就是脚本文件; -z表示其后的信息记录文件用于记录屏幕的输出&am…...

SpringBoot + FFmpeg实现一个简单的M3U8切片转码系统
简介 在本文中,我们将使用SpringBoot和FFmpeg来实现一个简单的M3U8切片转码系统。M3U8是一种常用的视频流媒体播放列表格式,而FFmpeg则是一个强大的音视频处理工具。 技术栈 SpringBoot:一个基于Spring框架的快速开发平台。FFmpeg…...
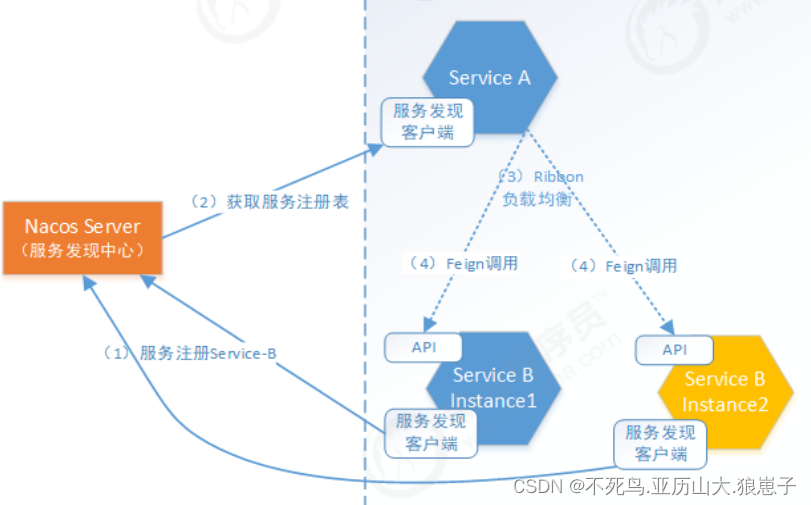
SpringCloud(35):Nacos 服务发现快速入门
本小节,我们将演示如何使用Spring Cloud Alibaba Nacos Discovery为Spring cloud 应用程序与 Nacos 的无缝集成。 通过一些原生的spring cloud注解,我们可以快速来实现Spring cloud微服务的服务发现机制,并使用Nacos Server作为服务发现中心,统一管理所有微服务。 1 Spring…...
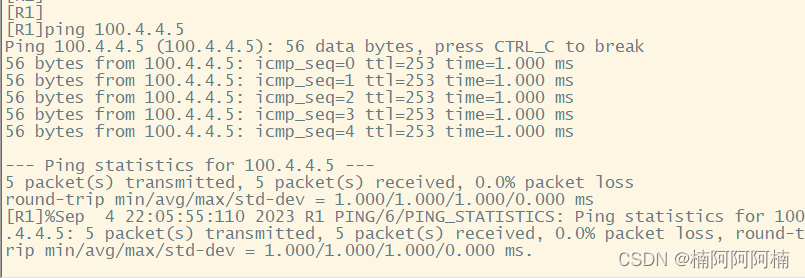
OSPF实验:配置与检测全网互通
文章目录 一、实验背景与目的二、实验拓扑三、实验需求四、实验解法1. 配置 IP 地址2. 按照图示分区域配置 OSPF ,实现全网互通3. 检查是否全网互通 摘要: 本篇文章介绍了一个 OSPF(Open Shortest Path First)实验,旨在…...

常见的五种设计模式
https://www.runoob.com/design-pattern/factory-pattern.html 单例模式 **意图:**保证一个类仅有一个实例,并提供一个访问它的全局访问点。 **主要解决:**一个全局使用的类频繁地创建与销毁。 **何时使用:**当您想控制实例数目…...

pandas读取一个 文件夹下所有excel文件
我这边有个需求,是要求汇总一个文件夹所有的excel文件, 其中有.xls和 .xlsx文件,同时还excel文件中的数据可能还不一致,会有表头数据不一样需要一起汇总。 首先先遍历子文件夹并读取Excel文件: 使用os库来遍历包含子文…...

Python网页请求超时如何解决
在进行网络爬虫项目时,我们经常需要发送大量的请求来获取所需的数据。然而,由于网络环境的不稳定性,请求可能会因为超时而失败。请求超时可能导致数据获取不完整,影响爬虫的效率和准确性。此外,频繁的请求超时可能会被…...

虚幻引擎集成web前端<二>:UE4 像素流 与 web 通信
Vue 和 Unreal Engine (UE) 之间的通信可以通过多种方式实现。以下是一些建议的方法: 使用 Websockets:Websockets 是一种在客户端和服务器之间进行双向通信的技术。在 Vue 端,你可以使用一个 Websockets 库(如 socket.io…...
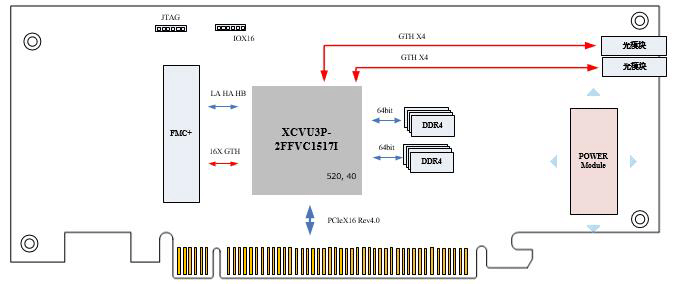
618-基于FMC+的XCVU3P高性能 PCIe 载板 设计原理图
基于FMC的XCVU3P高性能 PCIe 载板 一、板卡概述 板卡主控芯片采用Xilinx UltraScale16 nm VU3P芯片(XCVU3P-2FFVC1517I)。板载 2 组 64bit 的DDR4 SDRAM,支持 IOX16或者 JTAG 口,支持PCIe X 16 ReV3.0以及 FMC 扩展接口。…...

ABB UF C911B108 3BHE037864R010控制主板模块
ABB UF C911B108 3BHE037864R010 控制主板模块通常用于ABB的工业自动化和控制系统中,作为关键组件之一,用于执行控制、监测和通信任务。以下是通常情况下控制主板模块的一些产品功能: 高性能处理器:ABB UF C911B108 3BHE037864R01…...

基于SpringBoot开发的疫情信息管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 疫情信息管理系统,java项目。 eclipse和…...

手敲Cocos简易地图编辑器:人生地图是一本不断修改的书,每一次编辑都是为了克服新的阻挡
引言 本系列是《8年主程手把手打造Cocos独立游戏开发框架》,欢迎大家关注分享收藏订阅。 在上一篇文章,笔者给大家讲解了在Cocos独立游戏开发框架中,如何自定义实现Tile地图管理器,成功地在游戏中优化加载一张特大的地图。接下来…...

MySQL——修改数据库和表的字符编码
修改编码: (1)先停止服务 (2)修改my.ini文件 (3)重新启动服务说明: 如果是在修改my.ini之前建的库和表,那么库和表的编码还是原来的Latin1,要么删了重建,要么…...

中国人民大学与加拿大女王大学金融硕士——人生总要逼自己一把
我们每个人都是一个独特而丰富的个体,身上蕴藏着各种潜力和可能性。要不断去开发自己的潜能,不断学习和提升自己的知识和技能,保持对新知识和趋势的敏感。想要在职场上走得更远,就要逼自己一把,在职继续攻读硕士学位是…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
