Matlab 如何计算正弦信号的幅值和初始相角
Matlab 如何计算正弦信号的幅值和初始相角
1、概述
如果已知一个正弦信号的幅值,在FFT后频域上该信号谱线的幅值与设置值不同,而是大了许多;如果不知道某一正弦信号的幅値,又如何通FFT后在頻域上求出该正弦信号的幅值呢?
2、理论基础
有一正弦信号为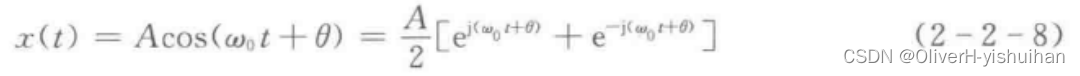
信号的幅值为 ,初始相角为
。以采样频率
采样后,FFT(DFT)只取有限项的 n 值(设共 N 项),其离散化表达式为:

式中: 。又进一步假设,正弦信号的频率
是
的整数倍(
是频谱中谱线之间频率间隔,或称为分辨率,即
),即有
,表示
是与FFT后频谱上的某根线谱相重合,可令
与第
条线谱相重合,即
,所以有
。由 k = 0 和 式(2-2-10)可得:
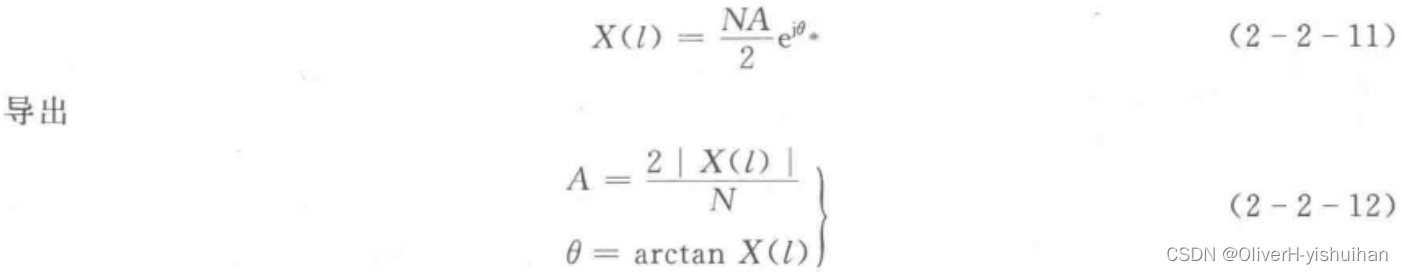 求出了信号幅值
求出了信号幅值,同时也求出了初始相角
。
- 这种方法求出正弦信号幅值
和初始相角
是在信号的頻率
与FFT后频谱上的某根谱线相重合的条件下。
- 如果
在两条谱线之间,則不能用这种方法来计算。这就是栅栏效应,我们可以用内插的方法来算信号在两条谱线之间分量的频率、幅值和初始相角。
- 当
时,不存在負頻率部分,所以
的幅値
,初始相角
。
- 同时从式(2-2-10)得到,对于所有
,设
,
,
,……,此时
,使
的
值均为0。
3、实例
例:设信号的采样频率为1000Hz,由两个余弦信号组成,频率分别为 f1=50Hz 和 f2=65.75Hz,幅值都为1,初始相角都为0,信号长度为1000,通过FFT求出两个正弦信号的幅值和初始相角。
程序如下:
% 例:设信号的采样频率为1000Hz,由两个余弦信号组成,频率分别为 f1=50Hz 和 f2=65.75Hz,
% 幅值都为1,初始相角都为0,信号长度为1000,通过FFT求出两个正弦信号的幅值和初始相角。% pr2_2_2
clc; close all; clear;fs = 1000; %采样频率
N = 1000; %信号长度
t = (0:N-1)/fs; %设置时间序列
f1 = 50;
f2 = 65.75; %信号2频率
x = cos(2*pi*f1*t) + cos(2*pi*f2*t); %设置信号
X = fft(x); %FFT
Y = abs(X)*2/N; %计算幅值
freq = (0:N/2)*fs/N; %设置频率刻度
[A1, k1] = max(Y(45:65)); %寻求第一个信号的幅值
k1 = k1 + 44; %修正索引号
[A2, k2] = max(Y(60:70)); %寻求第二个信号的幅值
k2 = k2 + 59; %修正索引号Theta1 = angle(X(k1));
Theta2 = angle(X(k2));
% 显示频率、幅值和初始相角
fprintf('f1=%5.2f A1=%5.4f Theta1=%5.4f\n',freq(k1),A1,Theta1);
fprintf('f2=%5.2f A2=%5.4f Theta2=%5.4f\n',freq(k2),A2,Theta2);% 作图
figure('Name','幅值频谱图')
subplot 211; plot(freq,Y(1:N/2+1),'k'); xlim([0 150]);
xlabel('频率/Hz'); ylabel('幅值'); title('频谱图');
subplot 223; stem(freq,Y(1:N/2+1),'k'); xlim([40 60]);
xlabel('频率/Hz'); ylabel('幅值'); title('50Hz分量');
subplot 224; stem(freq,Y(1:N/2+1),'k'); xlim([55 75]);
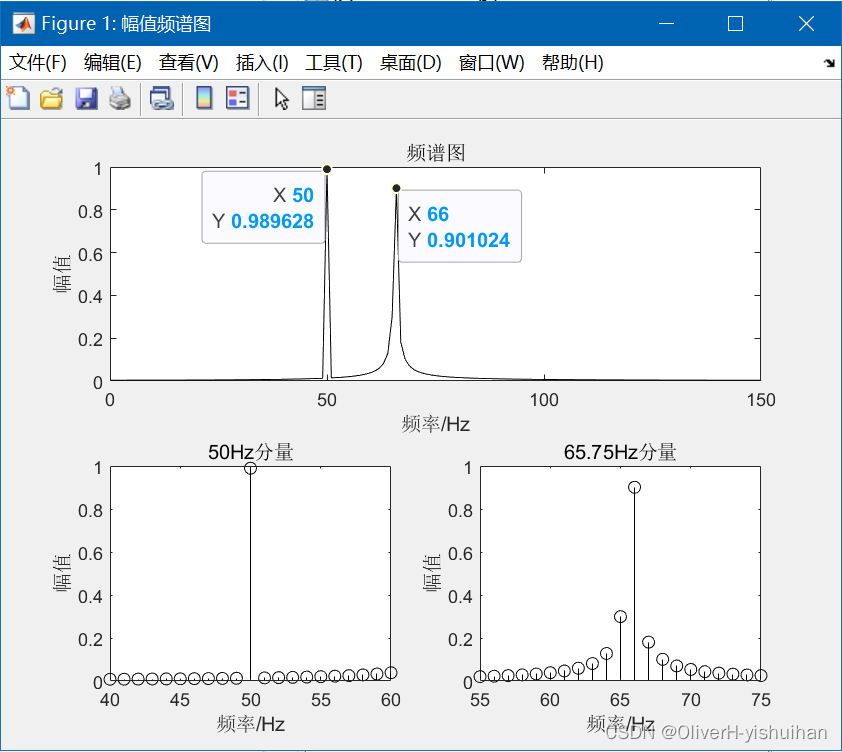
xlabel('频率/Hz'); ylabel('幅值'); title('65.75Hz分量');

其中 f1 和 f2 表示两信号的頻率,A1 和 A2 表示两信号的幅値,Thetal 和 Theta2 表示两信号的初始相角。第2个信号在两条谱线之间,所以出的参数有很大的差;而第1个信号非常接近设置值,但是有一定的误差,这完全是由第2个信号泄漏所造成的(可通过加窗函数处理该信号,以减少泄漏,对信号参数的估算値能更精确一些)。
相关文章:

Matlab 如何计算正弦信号的幅值和初始相角
Matlab 如何计算正弦信号的幅值和初始相角 1、概述 如果已知一个正弦信号的幅值,在FFT后频域上该信号谱线的幅值与设置值不同,而是大了许多;如果不知道某一正弦信号的幅値,又如何通FFT后在頻域上求出该正弦信号的幅值呢? 2、…...

华为hcie认证培训报班培训好?还是自学好
华为HCIE认证培训报班培训和自学各有优势。 培训的优势: 系统性学习:培训课程通常会系统地涵盖HCIE认证所需的各个知识点,帮助你建立全面的理论体系。指导与互动:培训中,能够与资深讲师互动,及时解答疑惑…...
ASP.NET+sqlserver通用电子病历管理系统
一、源码描述 这是一款简洁十分美观的ASP.NETsqlserver源码,界面十分美观,功能也比较全面,比较适合 作为毕业设计、课程设计、使用,感兴趣的朋友可以下载看看哦 二、功能介绍 该源码功能十分的全面,具体介绍如下&…...
wireshark通常无法抓取交换机所有端口报文
Wireshark 是一种网络分析工具,它通常在计算机的网络接口上进行数据包捕获和分析。然而,Wireshark 默认情况下无法直接捕获交换机所有端口的报文。 交换机是一种网络设备,它在局域网内转发数据包,根据目的MAC地址将数据包仅发送到…...

猫头虎的技术笔记:Spring Boot启动报错解决方案
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Istio网关流量转发
摘要 Istio网关转发到后端服务的步骤,可以按照以下详细说明进行操作: 配置Istio Sidecar:确保目标后端服务已经部署并成功运行,并为其启用Istio Sidecar。Istio Sidecar负责在Pod中注入Istio代理,以便实现流量控制和…...

阿里云acp云计算认证考试科目有哪些?
阿里云ACP云计算认证考试科目包括以下内容: 阿里云云计算基础知识:包括云计算的定义、特点、服务模式、部署模式、虚拟化技术等相关知识。阿里云产品:包括阿里云ECS、RDS、SLB、OSS、DNS等核心产品的架构、使用方法、优化技巧等相关知识。云…...

8、Spring security配置放过的请求又被拦截了
项目场景: 在项目中有一些接口需要放开spring security拦截,配置方法如下,其中permitUrls为需要放过的请求路径。 Override public void configure(WebSecurity web) {web.ignoring().antMatchers(permitUrls); }问题描述 实际请求地址&am…...

4.后端·新建子模块与开发(传统模式)
文章目录 学习资料新建子模块与各层查询entity的列表entitymapper层service层controller层 测试 学习资料 https://www.bilibili.com/video/BV13g411Y7GS?p8&spm_id_frompageDriver&vd_sourceed09a620bf87401694f763818a31c91e b站的学习视频 新建子模块与各层 在r…...

.netcore 连接 apache doris
apache doris 兼容mysql协议;所以我们在.netcore项目中,可以使用Mysql的驱动 dotnet add package MySqlConnector 测试代码: [HttpGet]public async Task<string> Get2(){//打开连接await using var connection new MySqlConnectio…...

【C语言】探讨常见自定义类型的存储形式
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:C语言 🔥该文章将探讨结构体,位段,共用体的存储形式。 目录: 🌍结构体内存对齐✉…...

NLP(六十九)智能文档问答助手升级
本文在笔者之前研发的大模型智能文档问答项目中,开发更进一步,支持多种类型文档和URL链接,支持多种大模型接入,且使用更方便、高效。 项目介绍 在文章NLP(六十一)使用Baichuan-13B-Chat模型构建智能文档中…...

如何使用SQL系列 之 如何在MySQL中使用索引
引言 关系数据库可用于处理任何大小的数据,包括包含数百万行的大型数据库。结构化查询语言(SQL)提供了一种基于特定条件在数据库表中查找特定行的简洁而直接的方法。随着数据库变得越来越大,在其中找到特定的行变得越来越困难,就像大海捞针一…...
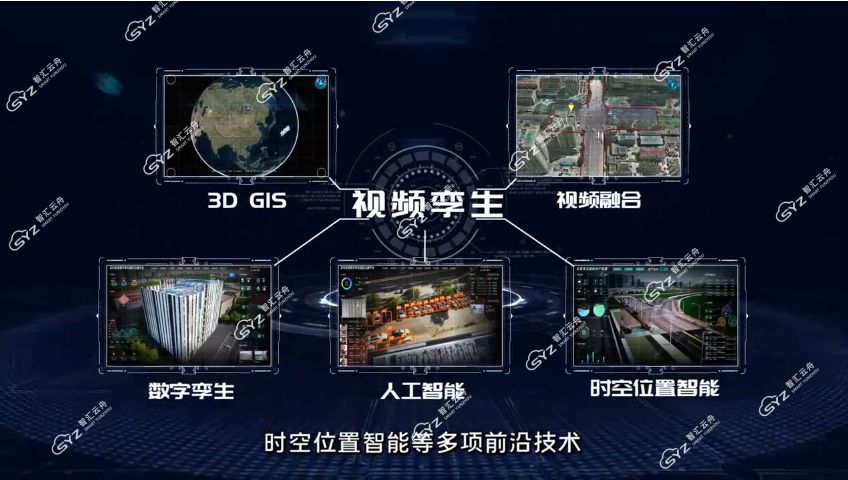
数字孪生相关政策梳理,重点对各行业版块的指导和引领
前言 数字孪生技术作为新型智慧城市建设的创新引领性技术,有利于打造孪生城市运行空间,强化城市大脑基础能力,实现全域时空数据融合。数字孪生技术在推动智慧城市建设方面的作用已越来越受到重视。2021年3月,《国家“十四五”规划…...

nios里面打开eclipse遇到Unresolved inclusion: “system.h“等问题
问题:在Nios中打开软核部分代码时,遇到一堆Unresolved inclusion: "system.h"等问题报错 原因:bsp文件和软核没关联,导致找不到头文件地址,关联一下就好 解决步骤: 右键bsp文件,点击…...

C#,数值计算——伽马微分(Gammadev)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { public class Gammadev : Normaldev { private double alph { get; set; } private double oalph { get; set; } private double bet { get; set; } private double a1 { g…...
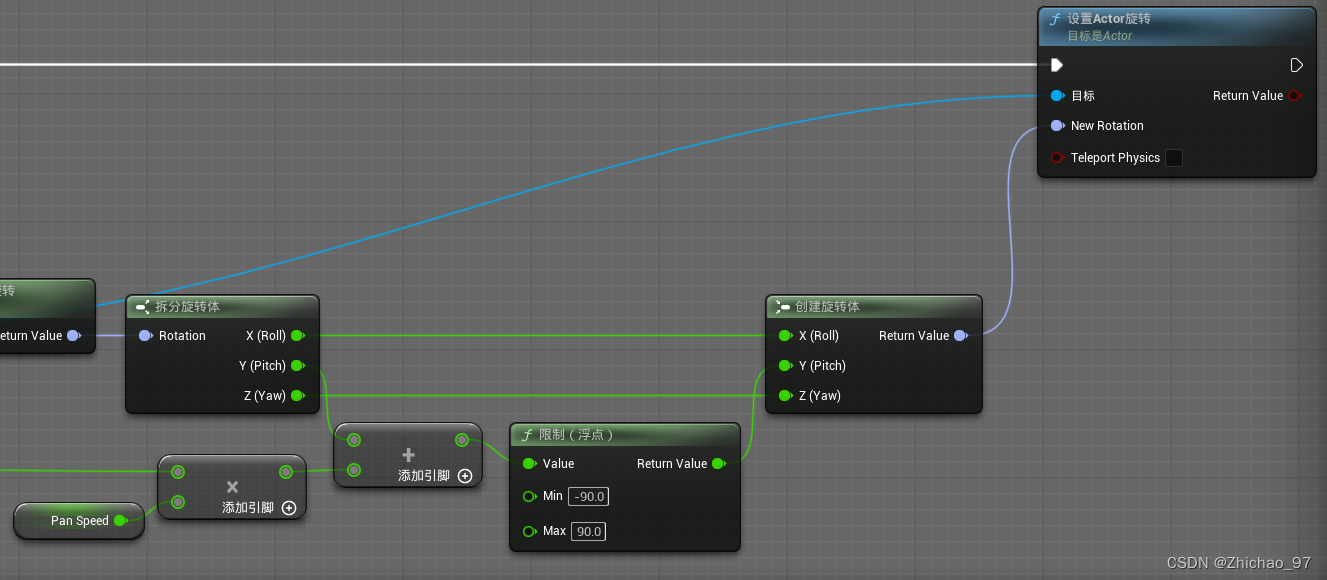
【UE5 智慧城市系列】5-通过鼠标键盘控制摄像机
目标 通过鼠标WASD键控制摄像机前后左右移动,鼠标滚轮控制弹簧臂长度的修改,鼠标中键控制摄像机旋转。 步骤 1. 首先创建一个游戏模式,这里命名为“BP_GameMode” 2. 再创建一个玩家控制器,这里命名为“BP_PlayerController” …...

工作纪实38-ES分页数据问题
之前分页查询有接ES,随着系统使用时间数据量不断增加,会有如下报错。关键信息就是 Result window is too large, from size must be less than or equal to: [10000] but was [100001] 当索引非常非常大(千万或亿),是无法按照from size做深…...
设计模式之访问器模式(Visitor)的C++实现
1、访问器模式的提出 在软件开发过程中,早已发布的软件版本,由于需求的变化,需要给某个类层次结构增加新的方法。如果在该基类和子类中都添加新的行为方法,将给代码原有的结构带来破坏,同时,也违反了修改封…...
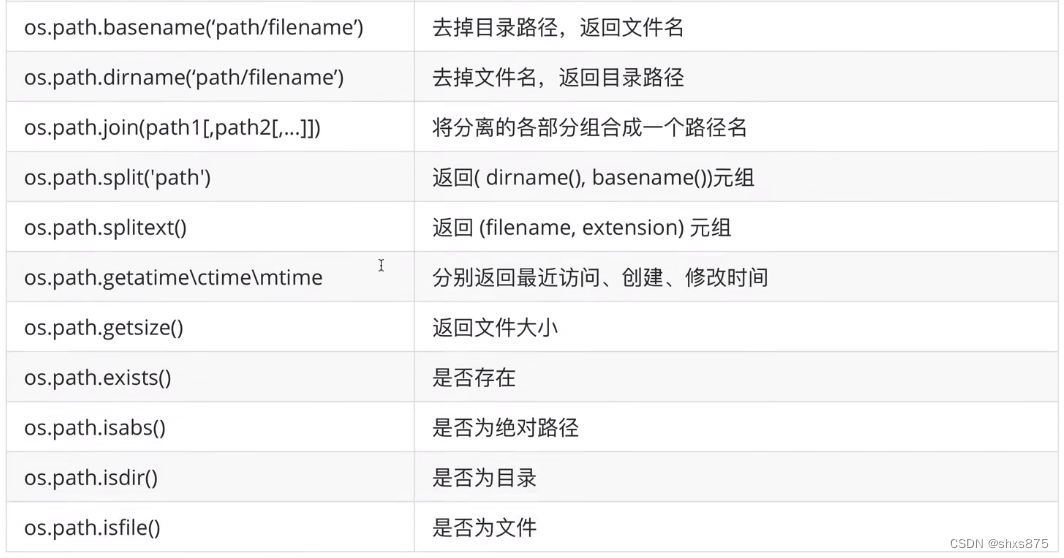
Python之OS模块
os模块负责程序与操作系统的交互,提供了访问操作系统底层的接口;即os模块提供了非常丰富的方法用来处理文件和目录。 使用的时候需要导入该模块:import os...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
