AB测试结果分析
一、假设检验
根据样本(小流量)的观测结果,拒绝或接受关于总体(全部流量)的某个假设,称为假设检验。
假设检验的基本依据是小概率事件原理(小概率事件几乎不发生),如果小概率事件发生了,则有充分理由推翻原假设,否则接受原假设,检验的具体过程是:
-
首先假定原假设成立,并寻找一个原假设成立条件下的发生概率微小的事件,称为检验事件,对应的统计量称为检验统计量
-
其次是采集样本
-
最后观测步骤 1 所定义的小概率事件是否发生
-
- 若小概率事件发生,则拒绝原假设,接受备用假设
- 若小搞错了时间未发生,则接受原假设,拒绝备用假设
具体到AB实验中,涉及实验组和对照组组两个总体,假设实验的某个目标指标满足正态分布,实验组和对照组分别记为 X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) X\sim \mathcal{N}(\mu_1, \sigma_1^2), Y \sim \mathcal{N}(\mu_2, \sigma_2^2) X∼N(μ1,σ12),Y∼N(μ2,σ22),常见检验问题是判断实验组对比对照组是否有效,具体又分为几类情况:
I. 原假设 H 0 : μ 1 ≤ μ 2 H_0: \mu_1\le \mu_2 H0:μ1≤μ2实验组对比对照组负向或无效;备用假设 H 1 : μ 1 > μ 2 H_1:\mu_1 > \mu_2 H1:μ1>μ2,实验组对比对照组正向
II. 原假设 H 0 : μ 1 ≥ μ 2 H_0:\mu_1\ge \mu_2 H0:μ1≥μ2实验对比对照组正向或无效;备用假设 H 1 : μ 1 < μ 2 H_1:\mu_1 < \mu_2 H1:μ1<μ2,实验组对比对照组负向
III. 原假设 H 0 : μ 1 = μ 2 H_0:\mu_1= \mu_2 H0:μ1=μ2实验对比对照组无效;备用假设 H 1 : μ 1 ≠ μ 2 H_1:\mu_1 \ne \mu_2 H1:μ1=μ2,实验有效,但未区分正向还是负向效果
与之等价的三个假设检验问题是:
I. 原假设 H 0 : μ 1 − μ 2 ≤ 0 H_0:\mu_1 - \mu_2 \le 0 H0:μ1−μ2≤0;备用假设 H 1 : μ 1 − μ 2 > 0 H_1:\mu_1 - \mu_2 > 0 H1:μ1−μ2>0
II. 原假设 H 0 : μ 1 − μ 2 ≥ 0 H_0:\mu_1- \mu_2\ge 0 H0:μ1−μ2≥0;备用假设 H 1 : μ 1 − μ 2 < 0 H_1:\mu_1 - \mu_2< 0 H1:μ1−μ2<0
III. 原假设 H 0 : μ 1 − μ 2 = 0 H_0:\mu_1- \mu_2 = 0 H0:μ1−μ2=0;备用假设 H 1 : μ 1 − μ 2 ≠ 0 H_1:\mu_1 - \mu_2 \ne 0 H1:μ1−μ2=0
如何寻找一个事件,满足在原假设成立条件下发生的概率微小 ?发生概率多小能满足要求 ?
第二个问题比较好回答,一般取 0.01 或 0.05,记为 α = 0.01 ∣ 0.05 \alpha = 0.01|0.05 α=0.01∣0.05,称为检验的显著性。第一个问题需要费一番推导。
以假设检验问题 I 为例,实验收集的样本记为 { X 1 , X 2 . . . , X n } , { Y 1 , Y 2 , . . . , Y 3 } \{X_1, X_2...,X_n\}, \{Y_1, Y_2, ..., Y_3\} {X1,X2...,Xn},{Y1,Y2,...,Y3}, 样本均值 X ‾ = ∑ i X i n , Y ‾ = ∑ i Y I m \overline{X} = \frac{\sum_i X_i}{n},\overline{Y} = \frac{\sum_iY_I}{m} X=n∑iXi,Y=m∑iYI分别总体均值 μ 1 , μ 2 \mu_1, \mu_2 μ1,μ2的无偏相合估计,样本均值之差 X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y是总体均值差 μ 1 − μ 2 \mu_1-\mu_2 μ1−μ2的无偏相合估计,因此样本均值之差 X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y大概率是分布在 μ 1 − μ 2 \mu_1-\mu_2 μ1−μ2附近,直观思考,原假设成立的条件下, X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y大概率落在非正数附近, X ‾ − Y ‾ \overline{X}-\overline{Y} X−Y取值为较大的正数的概率较小,如下图:
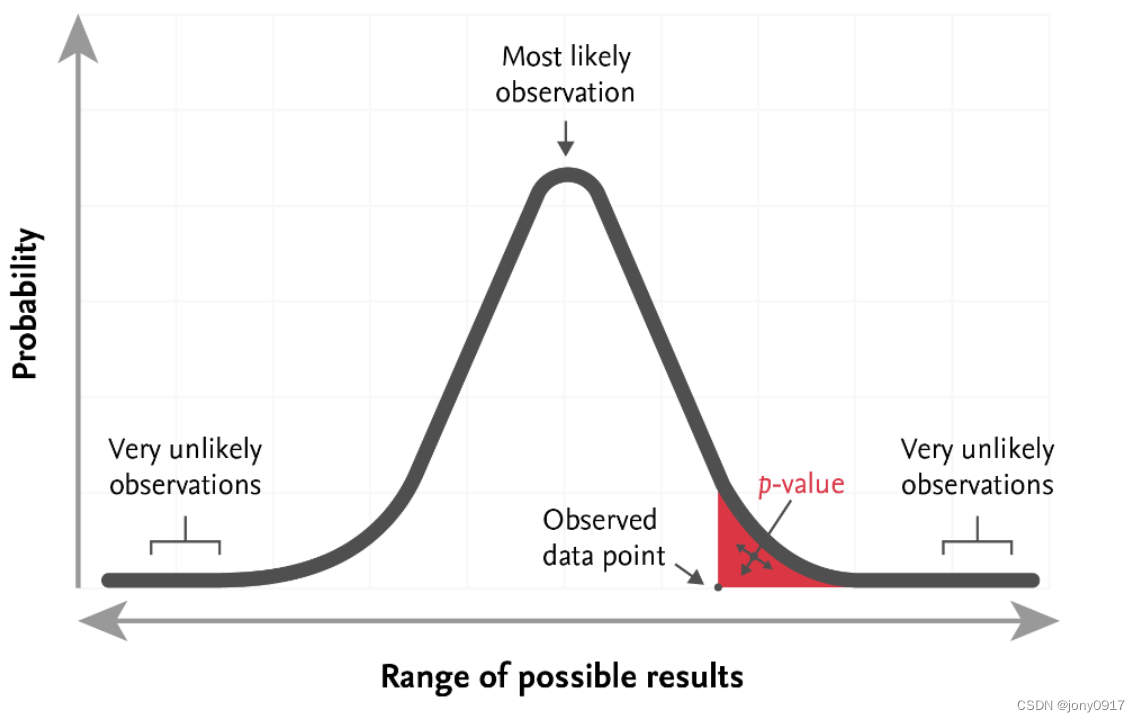
因此假设检验问题 I 原假设成立条件下的小概率事件定义为:$ {\overline{X}-\overline{Y} > c}$
下面需要做的是在给定小概率值 α \alpha α(也就是检验的显著性)的条件下确定阈值 c ,也就是满足不等式 P ( X ‾ − Y ‾ > c ) ≤ α P(\overline{X}-\overline{Y} > c) \le \alpha P(X−Y>c)≤α的实数 c.
由中心极限定理得到:
X ‾ ∼ N ( μ 1 , σ 1 2 / n ) Y ‾ ∼ N ( μ 2 , σ 2 2 / m ) \overline{X} \sim \mathcal{N}(\mu_1, \sigma_1^2/n)\\ \overline{Y} \sim \mathcal{N}(\mu_2, \sigma_2^2/m) X∼N(μ1,σ12/n)Y∼N(μ2,σ22/m)
为了确定阈值 c,需要分几种情况:
- 总体方差 σ 1 2 , σ 2 2 \sigma_1^2, \sigma_2^2 σ12,σ22已知
- 总体方差 σ 1 2 = σ 2 2 = σ 2 \sigma_1^2 = \sigma_2^2 = \sigma^2 σ12=σ22=σ2,且未知
- 总体方差 σ 1 2 ≠ σ 2 2 \sigma_1^2\ne\sigma_2^2 σ12=σ22,且未知
- 总体方差 σ 1 2 ≠ σ 2 2 \sigma_1^2\ne \sigma_2^2 σ12=σ22,且未知,大样本场景
首先考虑最简单的情况1, 由独立正态分布特性得到:
X ‾ − Y ‾ ∼ N ( μ 1 − μ 2 , σ 1 2 n + σ 2 2 m ) \overline{X}-\overline{Y} \sim \mathcal{N}(\mu_1 - \mu_2, \frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m} ) X−Y∼N(μ1−μ2,nσ12+mσ22)
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ∼ N ( 0 , 1 ) \frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \sim \mathcal{N}(0, 1) nσ12+mσ22(X−Y)−(μ1−μ2)∼N(0,1): 正态分布性质
P ( ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m > z α ) = α P(\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} > z_{\alpha}) =\alpha P(nσ12+mσ22(X−Y)−(μ1−μ2)>zα)=α : 由正态分布的上分位z_{\alpha}数定义
P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m − μ 1 − μ 2 σ 1 2 n + σ 2 2 m > z α ) = α P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha}) = \alpha PH0(nσ12+mσ22X−Y−nσ12+mσ22μ1−μ2>zα)=α
P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α + μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) = α P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha} + \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) = \alpha PH0(nσ12+mσ22X−Y>zα+nσ12+mσ22μ1−μ2)=α
P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α ) ≤ P H 0 ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α + μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) = α P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha}) \le P_{H_0}(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha} + \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) = \alpha PH0(nσ12+mσ22X−Y>zα)≤PH0(nσ12+mσ22X−Y>zα+nσ12+mσ22μ1−μ2)=α: 由事件和子事件概率关系
P H 0 ( X ‾ − Y ‾ > z α ∗ σ 1 2 n + σ 2 2 m ) ≤ α P_{H_0}(\overline{X}-\overline{Y} >z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}) \le \alpha PH0(X−Y>zα∗nσ12+mσ22)≤α
c = z α ∗ σ 1 2 n + σ 2 2 m c = z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}} c=zα∗nσ12+mσ22
概念整理:
-
检验显著性: α \alpha α
-
检验统计量:$Z= \overline{X}-\overline{Y} $
-
拒绝域: W I = { Z > z α ∗ σ 1 2 n + σ 2 2 m } W_I = \{ Z >z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\} WI={Z>zα∗nσ12+mσ22}
因为 { X ‾ − Y ‾ > z α ∗ σ 1 2 n + σ 2 2 m } \{\overline{X} - \overline{Y} > z_{\alpha} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\} {X−Y>zα∗nσ12+mσ22}与 { X ‾ − Y ‾ σ 1 2 n + σ 2 2 m > z α } \{ \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} >z_{\alpha} \} {nσ12+mσ22X−Y>zα}是等价事件,因此检验问题 1 经常采用的
- 检验统计量是 u = X ‾ − Y ‾ σ 1 2 n + σ 2 2 m u = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} u=nσ12+mσ22X−Y
- 拒绝域为 W I = { u > z α } W_I = \{u > z_{\alpha}\} WI={u>zα}
p-value:
以检验问题 I 为例
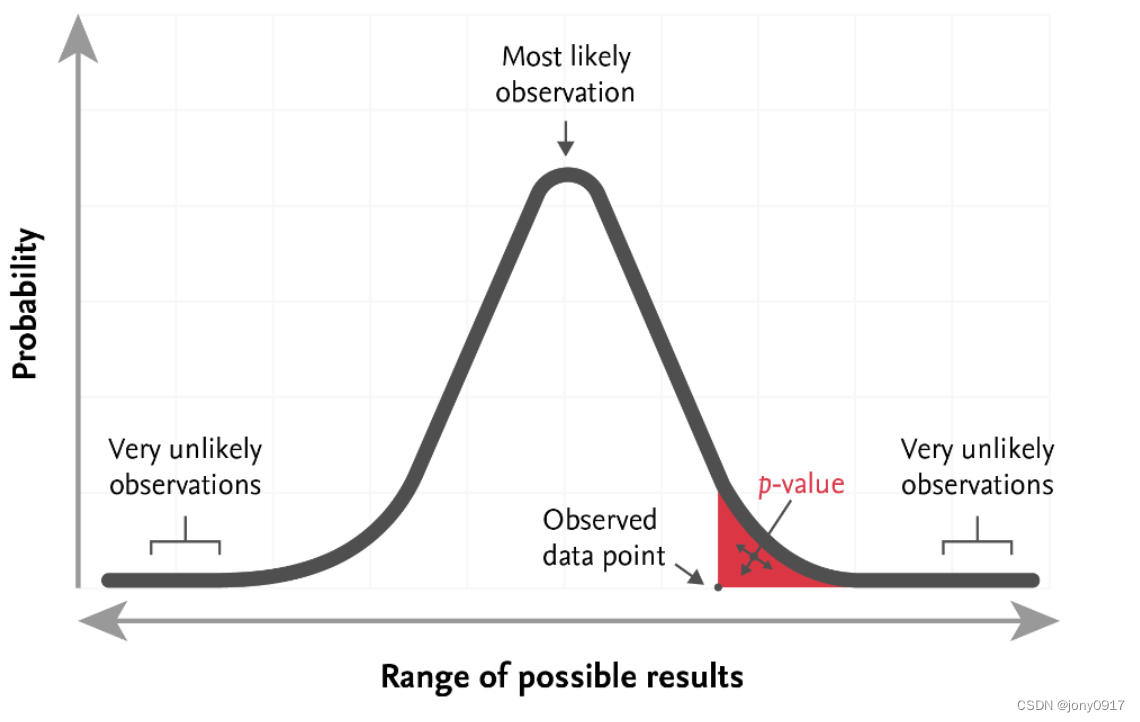
在一个假设检验问题中,拒绝原假设的最小显著性水平成为 p 值。
X ‾ − Y ‾ ∼ N ( μ 1 − μ 2 , σ 1 2 n + σ 2 2 m ) \overline{X}-\overline{Y} \sim \mathcal{N}(\mu_1 - \mu_2, \frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m} ) X−Y∼N(μ1−μ2,nσ12+mσ22)
p = P ( T > X ‾ − T ‾ ) p= P(T > \overline{X} - \overline{T}) p=P(T>X−T)
利用p值和给定的显著性水平 α \alpha α:
- 若 α ≥ p \alpha \ge p α≥p,则拒绝原假设
- 若 α < p \alpha < p α<p,则接受原假设
p 值越小,拒绝原假设的理由越充分。
检验错误:
原假设实际成立但被拒绝的错误,称为 I 类错误,对应AB实验中推全了一个没有效果的实验,错误发生的概率记为 α \alpha α
原假设实际不成立但被接受的错误,称为 II 类错误,对应AB实验中一个有效果的实验没被推全,错误发生概率记为 β \beta β.
以上的检验过程保证原假设成立但被推翻的概率小于\alpha.
样本量一定的情况下,无法同事降低I类错误和II类错误的概率,一般通过保证 I 类错误不高于一个阈值的情况下,通过增大样本量,控制II错误概率。
最小样本量:
以检验问题 I 为例,考察接受原假设的概率:
P ( X ‾ − Y ‾ σ 1 2 n + σ 2 2 m < z α ) = P ( ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m < z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) P(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{\alpha}) = P(\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} ) P(nσ12+mσ22X−Y<zα)=P(nσ12+mσ22(X−Y)−(μ1−μ2)<zα−nσ12+mσ22μ1−μ2)
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ∼ N ( 0 , 1 ) \frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \sim \mathcal{N}(0, 1) nσ12+mσ22(X−Y)−(μ1−μ2)∼N(0,1)
P ( ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m < z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) = Φ ( z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m ) < β P(\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) = \Phi(z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}}) < \beta P(nσ12+mσ22(X−Y)−(μ1−μ2)<zα−nσ12+mσ22μ1−μ2)=Φ(zα−nσ12+mσ22μ1−μ2)<β
z α − μ 1 − μ 2 σ 1 2 n + σ 2 2 m < z 1 − β z_{\alpha} - \frac{\mu_1-\mu_2}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} < z_{1 - \beta} zα−nσ12+mσ22μ1−μ2<z1−β
假设 m = n
n > ( z α + z β ) σ 1 2 + σ 2 2 μ 1 − μ 2 ( 1 ) \sqrt{n} > \frac{(z_\alpha + z_\beta)\sqrt{\sigma_1^2 + \sigma^2_2}}{\mu_1 - \mu_2} \space\space\space\space\space\space(1) n>μ1−μ2(zα+zβ)σ12+σ22 (1)
启发:
-
指标总体的方差越大,需要的最小样本量越大
-
控制错误概率越低,需要的最小样本量越大,一般 α = 0.01 、 0.05 , β = 0.2 \alpha = 0.01、0.05, \beta = 0.2 α=0.01、0.05,β=0.2
-
实验组相对对照组提升 μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2越大,需要的样本量越小;提升越小,需要的最小样本量越大
-
- 当 μ 1 \mu_1 μ1从左侧无限接近 μ 2 \mu_2 μ2,所需要的最小样本量接近无限大
-
实验最短观测周期:T = ( z α + z β ) σ 1 2 + σ 2 2 μ 1 − μ 2 \frac{(z_\alpha + z_\beta)\sqrt{\sigma_1^2 + \sigma^2_2}}{\mu_1 - \mu_2} μ1−μ2(zα+zβ)σ12+σ22 / 单位时长累积样本数量
第2种情况,样本方差未知但相等:
s x 2 = 1 n − 1 ∑ ( x i − x ‾ ) 2 s y 2 = 1 m − 1 ∑ ( y i − y ‾ ) 2 s w 2 = ( n − 1 ) s x 2 + ( m − 1 ) s y 2 n + m − 2 s_x^2 = \frac{1}{n-1}\sum (x_i - \overline{x})^2 \\ s_y^2 = \frac{1}{m-1}\sum(y_i - \overline{y})^2 \\ s_w^2 = \frac{(n-1)s_x^2 + (m-1)s_y^2}{n+m-2} sx2=n−11∑(xi−x)2sy2=m−11∑(yi−y)2sw2=n+m−2(n−1)sx2+(m−1)sy2
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) s w 1 n + 1 m ∼ t ( n + m − 2 ) \frac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{s_w\sqrt{\frac{1}{n} + \frac{1}{m}}} \sim t(n + m - 2) swn1+m1(X−Y)−(μ1−μ2)∼t(n+m−2)
-
检验统计量: t = X ‾ − Y ‾ s w 1 n + 1 m t = \frac{\overline{X} - \overline{Y}}{s_w\sqrt{\frac{1}{n} + \frac{1}{m}}} t=swn1+m1X−Y
-
拒绝域: W I = { t > t 1 − α ( n + m − 2 ) } W_I = \{ t > t_{1-\alpha}(n + m- 2) \} WI={t>t1−α(n+m−2)}
第3中情况,样本样本方差未知,但不等
-
检验统计量: t = X ‾ − Y ‾ s x 2 n + s y 2 m t = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{s^2_x}{n} + \frac{s_y^2}{m}}} t=nsx2+msy2X−Y
-
拒绝域: W I = { t > t 1 − α ( l ) } l = ( s x 2 n + s y 2 m ) 2 / [ s x 4 n 2 ( n − 1 ) + s y 4 m 2 ( m − 1 ) ] W_I = \{ t > t_{1-\alpha}(l) \} \\ l = (\frac{s_x^2}{n} + \frac{s_y^2}{m})^2/[\frac{s_x^4}{n^2(n-1)} +\frac{s_y^4}{m^2(m-1)} ] WI={t>t1−α(l)}l=(nsx2+msy2)2/[n2(n−1)sx4+m2(m−1)sy4]
第4种情况,大样本情况
- 检验统计量: u = X ‾ − Y ‾ s x 2 n + s y 2 m u = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{s^2_x}{n} + \frac{s_y^2}{m}}} u=nsx2+msy2X−Y
- 拒绝域: W I = { u > z α } W_I = \{u > z_{\alpha}\} WI={u>zα}
二、区间估计
点估计不能提供估计参数的估计误差大小,所以点估计主要用在定性分析的场景,或在对总体参数要求不精确时使用,而在需要用精确总体参数的数据进行决策时则很少使用,这种场景主要使用区间估计。
第1种情况,总体方差已知:
( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ∼ N ( 0 , 1 ) \frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \sim \mathcal{N}(0, 1) nσ12+mσ22(X−Y)−(μ1−μ2)∼N(0,1)
P ( − z α / 2 ≤ ( X ‾ − Y ‾ ) − ( μ 1 − μ 2 ) σ 1 2 n + σ 2 2 m ≤ z α / 2 ) = 1 − α P(-z_{\alpha/2}\le\frac{(\overline{X}-\overline{Y}) - (\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}} \le z_{\alpha/2}) = 1- \alpha P(−zα/2≤nσ12+mσ22(X−Y)−(μ1−μ2)≤zα/2)=1−α
P ( X ‾ − Y ‾ − z α / 2 ∗ σ 1 2 n + σ 2 2 m ≤ μ 1 − μ 2 ≤ X ‾ − Y ‾ + z α / 2 ∗ σ 1 2 n + σ 2 2 m ) = 1 − α P(\overline{X}-\overline{Y} - z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}\le \mu_1-\mu_2\le \overline{X}-\overline{Y} + z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}) = 1 - \alpha P(X−Y−zα/2∗nσ12+mσ22≤μ1−μ2≤X−Y+zα/2∗nσ12+mσ22)=1−α
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − z α / 2 ∗ σ 1 2 n + σ 2 2 m , X ‾ − Y ‾ + z α / 2 ∗ σ 1 2 n + σ 2 2 m ] [\overline{X}-\overline{Y} - z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}, \overline{X}-\overline{Y} + z_{\alpha/2} * \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m}}] [X−Y−zα/2∗nσ12+mσ22,X−Y+zα/2∗nσ12+mσ22]
第2种情况,总体方差未知但相等:
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − t 1 − α / 2 ( n + m − 2 ) ∗ s w ∗ 1 n + 1 m , X ‾ − Y ‾ + t 1 − α / 2 ( n + m − 2 ) ∗ s w ∗ 1 n + 1 m ] [\overline{X}-\overline{Y} - t_{1-\alpha/2}(n+m-2)*s_w * \sqrt{\frac{1}{n} + \frac{1}{m}}, \overline{X}-\overline{Y} + t_{1-\alpha/2}(n+m-2) *s_w* \sqrt{\frac{1}{n} + \frac{1}{m}}] [X−Y−t1−α/2(n+m−2)∗sw∗n1+m1,X−Y+t1−α/2(n+m−2)∗sw∗n1+m1]
第3种情况:
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − t 1 − α / 2 ( 1 ) ∗ s x 2 n + s y 2 m , X ‾ − Y ‾ + t 1 − α / 2 ( l ) ∗ s x 2 n + s y 2 m ] [\overline{X}-\overline{Y} - t_{1-\alpha/2}(1) * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}, \overline{X}-\overline{Y} + t_{1-\alpha/2}(l) * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}] [X−Y−t1−α/2(1)∗nsx2+msy2,X−Y+t1−α/2(l)∗nsx2+msy2]
第4种情况:
- μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2的 1 − α 1 -\alpha 1−α置信区间 [ X ‾ − Y ‾ − u 1 − α / 2 ∗ s x 2 n + s y 2 m , X ‾ − Y ‾ + u 1 − α / 2 ∗ s x 2 n + s y 2 m ] [\overline{X}-\overline{Y} - u_{1-\alpha/2} * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}, \overline{X}-\overline{Y} + u_{1-\alpha/2} * \sqrt{\frac{s_x^2}{n} + \frac{s_y^2}{m}}] [X−Y−u1−α/2∗nsx2+msy2,X−Y+u1−α/2∗nsx2+msy2]
三、区间估计与假设检验的关系
- 若检验显著水平 α \alpha α 拒绝域为W,则对立事件 W ‾ \overline{W} W就是相应参数的 1 − α 1 - \alpha 1−α置信区间
- W ‾ \overline{W} W为相应参数 1 − α 1 - \alpha 1−α置信区间,则对立事件W为检验显著水平 α \alpha α的拒绝域
四、更多
两个二项分布指标的分析
。。。
相关文章:

AB测试结果分析
一、假设检验 根据样本(小流量)的观测结果,拒绝或接受关于总体(全部流量)的某个假设,称为假设检验。 假设检验的基本依据是小概率事件原理(小概率事件几乎不发生),如果…...

Python模块和包:sys模块、os模块和变量函数的使用
文章目录 模块(module)引入外部模块引入部分内容包 (package)示例代码开箱即用sys模块sys.argvsys.modulessys.pathsys.platformsys.exit() os模块os.environos.system()os模块中的变量、函数和类 测试代码模块中的变量和函数的使用 总结:pyt…...
计算机软件工程毕业设计题目推荐
文章目录 0 简介1 如何选题2 最新软件工程毕设选题3 最后 0 简介 学长搜集分享最新的软件工程业专业毕设选题,难度适中,适合作为毕业设计,大家参考。 学长整理的题目标准: 相对容易工作量达标题目新颖 1 如何选题 最近非常多的…...

嵌入式学习笔记(25)串口通信的基本原理
三根通信线:Tx Rx GND (1)任何通信都要有信息作为传输载体,或者有线的或则无线的。 (2)串口通信时有线通信,是通过串口线来通信的。 (3)串口通信最少需要2根ÿ…...

c++学习第十三
1)循环引用的案例及解决办法: #include <iostream> #include <memory> using namespace std; class A;class B { public:B(){cout<<"B constructor---"<<endl;}~B(){cout<<"B deconstructor----"<<endl;}std::weak_…...
java复习-线程的同步和死锁
线程的同步和死锁 同步问题引出 当多个线程访问同一资源时,会出现不同步问题。比如当票贩子A(线程A)已经通过了“判断”,但由于网络延迟,暂未修改票数的间隔时间内,票贩子B(线程B)…...

Qt指示器设置
目录 1. 样式设置 2. 行为设置 3. 交互设置 创建一个进度指示器控件 在Qt中设置指示器(Indicator)的外观和行为通常需要操作相关部件的属性和样式表。以下是如何在Qt中设置指示器的一些常见方式: 1. 样式设置 你可以使用样式表…...
计算机网络第四节 数据链路层
一,引入数据链路层的目的 1.目的意义 数据链路层是体系结构中的第二层; 从发送端来讲,物理层可以将数据链路层交付下来的数据,装换成光,电信号发送到传输介质上了 从接收端来讲,物理层能将传输介质的光&…...
Vue.js not detected解决方法
扩展程序》管理扩展程序》详情》允许访问文件地址打开...

Window10安装PHP7.4
1. 下载PHP 7 首先需要下载PHP 7的安装包,可以从PHP官网(https://www.php.net/downloads.php)或者Windows下的PHP官网(http://windows.php.net/download/)下载Windows版本的PHP 7安装包。根据自己的系统架构ÿ…...
【C++刷题】二叉树进阶刷题
根据二叉树创建字符串 class Solution { public:/** ()的省略有两种情况* 1.左右都为空,省略* 2.左子树不为空,右子树为空,省略*/string tree2str(TreeNode* root){string s;if(root nullptr){return s;}s to_string(root->val);if(root…...

有效的数独
有效的数独 题目: 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。示例 1: 输…...

Vue导航守卫beforeRouteEnter,beforeRouteUpdate,beforeRouteLeave
Vue导航守卫以我自己的理解就是监听页面进入,修改,和离开的功能。每个守卫接受三个参数 to: Route: 即将要进入的目标路由对象 from: Route: 当前导航正要离开的路由 next: Function: 一定要调用该方法来 resolve 这个钩子。执行效果依赖 next 方法的调用参数。 next(): 进行…...

小红书《乡村振兴战略下传统村落文化旅游设计》中南大许少辉八一新著
小红书《乡村振兴战略下传统村落文化旅游设计》中南大许少辉八一新著...

Android13 下拉菜单栏中添加快捷截图按钮
Android 13 原生系统下拉状态栏中是没有快捷截图按钮,现在需要添加快捷截图功能。 添加快捷截图功能后的效果图: 涉及修改的文件如下: modified: vendor/mediatek/proprietary/packages/apps/SystemUI/res/values/config.xml modified: vendor/mediatek/proprietary/…...
GFS文件系统
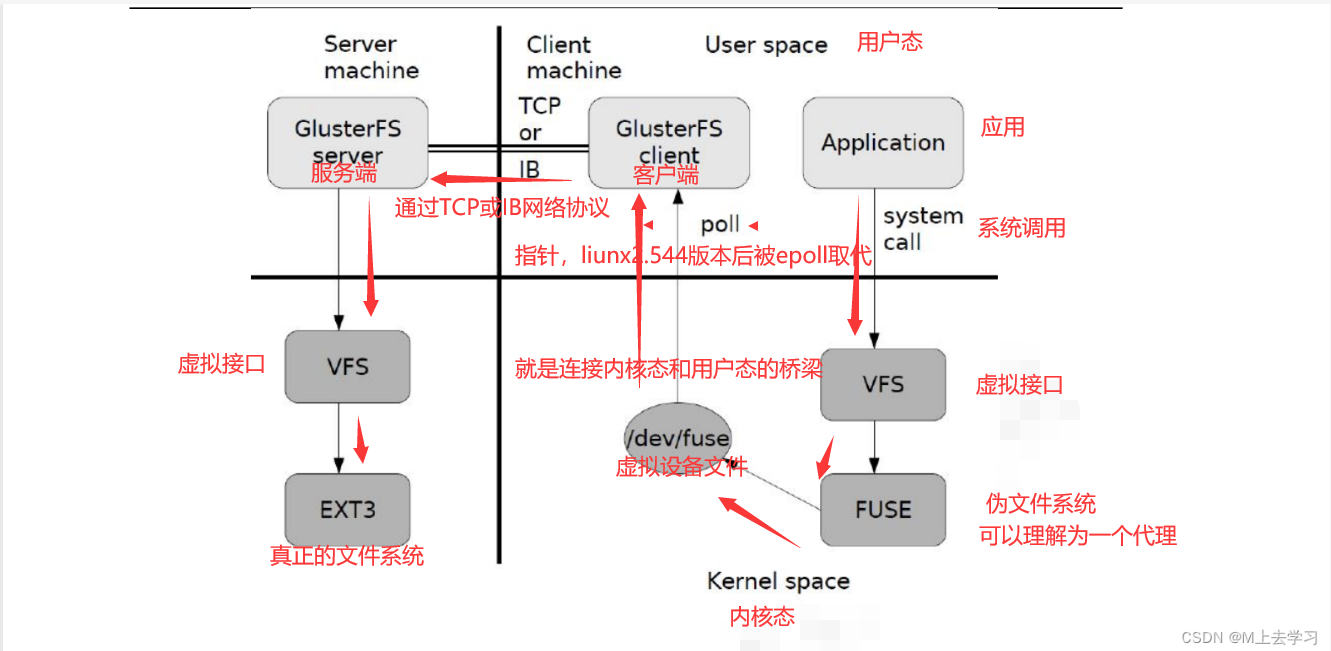
GFS 分布式文件系统 GlusterFS简介 GlusterFS 是一个开源的分布式文件系统。 由存储服务器、客户端以及NFS/Samba 存储网关(可选,根据需要选择使用)组成。 没有元数据服务器组件,这有助于提升整个系统的性能、可靠性和稳定性。 …...
22 相交链表
相交链表 题解1 快慢双指针改进 (acb bca)题解2 哈希表(偷懒) 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 题目数据 保证 整个链式结构中不存在环。 注意ÿ…...

简历(快速上手)
简历 文章目录 简历简历模板:排版上:内容上:沟通上: 简历在面试中起到关键作用 网申,HR只会花10秒多来看一下 内推,如果简历没优势就只能pass 简历模板: ⽊及简历(推荐! ) : https://resume.mdedit.online 排版上: 尽量简洁,…...
wpf复制xaml及其cs窗体到其他项目 添加现有项,选 .xaml.cs,点添加即可。VS2022
添加现有项,选 LoadingWindow.xaml.cs,点添加即可。...

在线旅游平台步入新时代,携程如何走出自己的路?
今年旅游从线下到线上全方位火了。有统计数据,一季度,光是抖音,旅游达人发布视频数量就高达175万条,播放量1350亿次,收获27亿次点赞。在这一趋势下,许多“不出名”的景区和酒店借势抖音达人完成“出圈”。短…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
