算法训练营day45|动态规划 part07:完全背包 (LeetCode 70. 爬楼梯(进阶)、322. 零钱兑换、279.完全平方数)
文章目录
- 70. 爬楼梯(进阶)(求排列方法数)
- 思路分析
- 代码实现
- 322. 零钱兑换(求等于背包重量的最小物品数)
- 思路分析
- 代码实现
- 思考总结
- 279.完全平方数 (求等于背包重量的最小物品数)
- 思路分析
- 代码实现
70. 爬楼梯(进阶)(求排列方法数)
题目链接🔥
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2: 输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
思路分析
之前讲这道题目的时候,因为还没有讲背包问题,所以就只是讲了一下爬楼梯最直接的动规方法(斐波那契)。这次再用背包做一遍。
这就是一个完全背包的排列问题。
- 确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
- 确定递推公式
求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
本题呢,dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j]
- dp数组如何初始化
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
下标非0的dp[i]初始化为0,因为dp[i]是靠dp[i-j]累计上来的,dp[i]本身为0这样才不会影响结果
- 确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
所以需将target放在外循环,将nums放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
- 举例来推导dp数组
代码实现
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1, 0);dp[0] = 1;for (int i = 1; i <= n; i++) { // 遍历背包for (int j = 1; j <= m; j++) { // 遍历物品if (i - j >= 0) dp[i] += dp[i - j];}}return dp[n];}
};
代码中m表示最多可以爬m个台阶,代码中把m改成2就是本题可以AC的代码了。
322. 零钱兑换(求等于背包重量的最小物品数)
题目链接🔥🔥
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
示例 4:
输入:coins = [1], amount = 1
输出:1
示例 5:
输入:coins = [1], amount = 2
输出:2
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 2^31 - 1
0 <= amount <= 10^4
思路分析
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
- 确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
- 确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
所以本题的两个for循环的关系是:外层for循环遍历物品,内层for遍历背包或者外层for遍历背包,内层for循环遍历物品都是可以的!
- 举例推导dp数组
以输入:coins = [1, 2, 5], amount = 5为例

代码实现
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1,INT_MAX-1);dp[0]=0;for(int i=0;i<coins.size();i++){for(int j=coins[i];j<=amount;j++){dp[j]=min(dp[j],dp[j-coins[i]]+1);}}if(dp[amount]!=INT_MAX-1) return dp[amount];else return -1;}
};
思考总结
本题是要求最少硬币数量,硬币是组合数还是排列数都无所谓!所以两个for循环先后顺序怎样都可以!
279.完全平方数 (求等于背包重量的最小物品数)
题目链接🔥🔥
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 10^4
思路分析
完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
跟上道题其实一模一样,直接看代码吧
代码实现
class Solution {
public:int numSquares(int n) {vector<int> dp(n+1,INT_MAX);dp[0]=0;for(int i=1;i*i<=n;i++){for(int j=i*i;j<=n;j++){dp[j]=min(dp[j],dp[j-i*i]+1);}}return dp[n];}
};
这里dp初始化成INT_MAX而不用担心dp[j-i*i]+1越界,因为物品里面有1,不管背包容量是多少,一定可以凑成。
相关文章:

算法训练营day45|动态规划 part07:完全背包 (LeetCode 70. 爬楼梯(进阶)、322. 零钱兑换、279.完全平方数)
文章目录 70. 爬楼梯(进阶)(求排列方法数)思路分析代码实现 322. 零钱兑换(求等于背包重量的最小物品数)思路分析代码实现思考总结 279.完全平方数 (求等于背包重量的最小物品数)思路分析代码实现 70. 爬楼梯(进阶)(求排列方法数) 题目链接🔥 假设你正在爬楼梯。需…...

【大模型】更强的开源可商用的中英文大语言模型baichuan2来了,从零开始搭建
【大模型】更强的开源可商用的中英文大语言模型baichuan2来了,从零开始搭建 Baichuan 2 介绍技术报告github 地址 模型下载开放协议协议 测试评估通用领域测试7B 模型结果13B 模型结果 法律、医疗7B 模型结果13B 模型结果 数学、代码7B 模型结果13B 模型结果 多语言…...
ElasticSearch系列-简介与安装详解
全文检索 讲ElasticSearch之前, 需要先提一下全文检索.全文检索是计算机程序通过扫描文章中的每一个词,对每一个词建立一个索引,指明该词在文章中出现的次数和位置。当用户查询时根据建立的索引查找,类似于通过字典的检索字表查字的过程。 …...
(07))
Layui + Flask | 表单组件(组件篇)(07)
http://layui.dev/docs/2.8/form 表单组件 form 是包含输入框、选择框、复选框、开关、单选框等表单项组件的集合,主要用于对表单域进行各类动态化渲染和相关的交互操作。form是 Layui 最常用的组件之一。 表单布局 form 组件自身的普通布局。其要点为: 通过 class="lay…...

【实践篇】Redis最强Java客户端Redisson
文章目录 1. 前言2. Redisson基础概念2.1 数据结构和并发工具2.1.1 对Redis原生数据类型的封装和使用2.1.2 分布式锁实现和应用2.1.3 分布式集合使用方法 2.2 Redisson的高级特性2.2.1 分布式对象实现和使用2.2.2 分布式消息队列实现和使用2.2.3 分布式计数器实现和使用 3. 参考…...
esxi扩容磁盘
esxi扩容磁盘 fdisk -l没用扩容 登录Esxi管理界面扩容磁盘 进入服务器查看 没用变化 (有些可能进去磁盘就是更新,直接就是扩容的,但是没扩容就需要执行下面的命令) [root234-ces /]# fdisk -l Disk /dev/sda: 85.9 GB, 858993…...
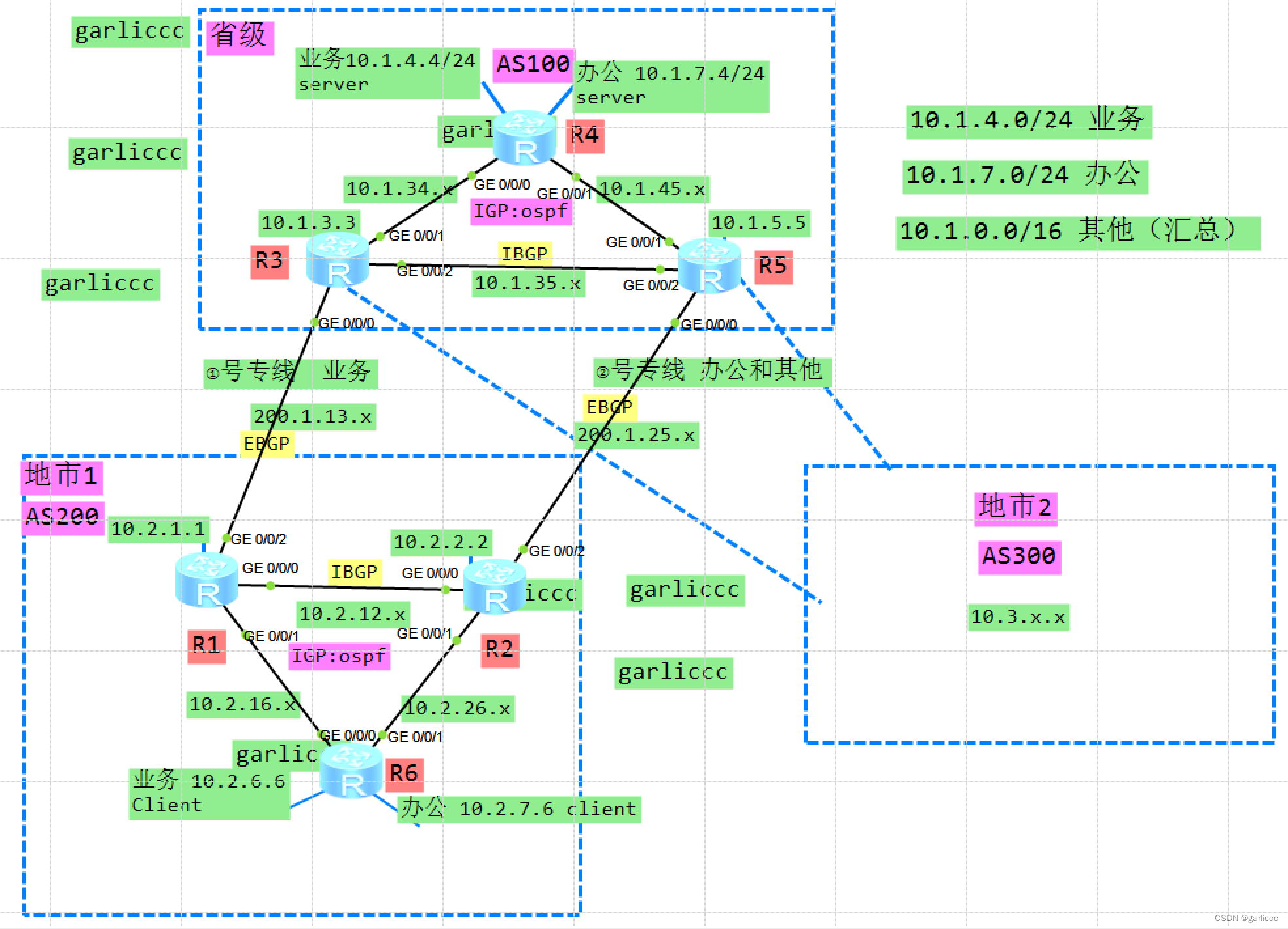
核心实验21_BGP高级(了解)(配置略)_ENSP
项目场景: 核心实验21_BGP基础_ENSP 通过bgp实现省市互通。 实搭拓扑图: 具体操作: 其他基础配置略(接口地址,ospf) 1.BGP邻居建立: R1: [R1]bgp 200 [R1-bgp]peer 10.2.2.2 as-number 200 …...

宝塔安装python和openssl
宝塔安装python和openssl OpenSSL Centos7 openssl 升级 1.1.1k.tar.gz centos7系统安装Vicuna(小羊驼)聊天机器人 CentOS中输入yum报错:sudo: unable to execute /bin/yum: No such file or directory opensslrpm安装指南-让你的网站更加…...

TDengine 3.1.1.0 来啦!更新如下
自 3.0 版本发布以来,在研发人员和社区用户的不断努力下,TDengine 做了大量更新,产品稳定性和易用性也在不断提升。近日,TDengine 3.1.1.0 成功发布,本文将向大家简单介绍一下该版本涉及的重大更新。 写在前面 伴随 …...

YSA Toon (Anime/Toon Shader)
这是一个Toon着色器/Cel阴影着色器,用于Unity URP 此着色器的目的是使角色或物体阴影实时看起来尽可能接近真实的动画或卡通效果 可以用于游戏,渲染,插图等 着色器特性,如:面的法线平滑、轮廓修复、先进的边缘照明、镜面照明、完全平滑控制 这个文档包括所有的功能https:/…...
LabVIEW通过IEC61508标准验证ITER联锁系统
LabVIEW通过IEC61508标准验证ITER联锁系统 保护环境要求系统能够保护机器免受工厂系统故障或机器危险操作造成的严重损坏。负责此功能的ITER系统是联锁控制系统(ICS)。该系统通过中央联锁系统(CIS)监督和控制不同的工厂联锁系统&…...

如何处理日期和时间?
处理日期和时间是计算机编程中的常见任务,无论是在C语言还是其他编程语言中。C语言提供了一些库函数来处理日期和时间,主要是通过<time.h>头文件中的函数来完成的。在本文中,我将详细解释如何在C语言中处理日期和时间,包括日…...
【开发】视频集中存储/直播点播平台EasyDSS点播文件分类功能优化
视频推拉流EasyDSS视频直播点播平台,集视频直播、点播、转码、管理、录像、检索、时移回看等功能于一体,可提供音视频采集、视频推拉流、播放H.265编码视频、存储、分发等视频能力服务。 TSINGSEE青犀视频的EasyDSS平台具有点播文件分类展示方法…...
论文多级编号-word2010
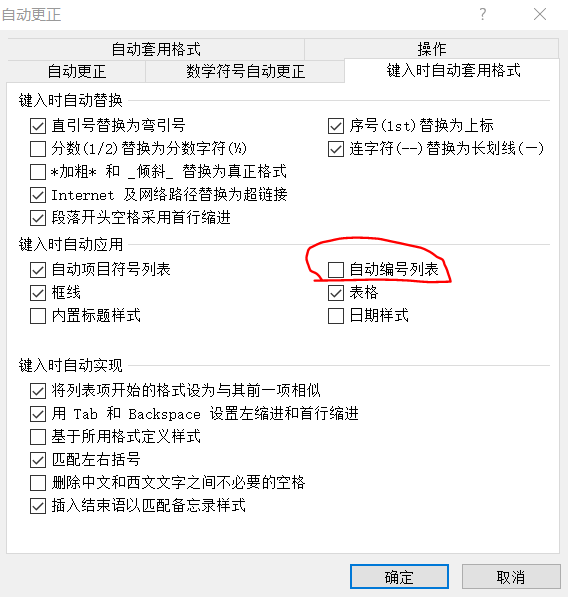
多级列表-定义新的多级列表 注意1.1中的两个1必须是灰色(如果不是灰色,解决方法放在文本文末了) 如果定义过程中发现1.1中的1不是灰色,如下图,那么需要操作下述步骤 点击文件-选项 取消勾选自动编号列表。确定后关闭文…...
Jetpack Compose基础组件之 — Text
Text的源码参数预览 Composable fun Text(text: String,modifier: Modifier Modifier,color: Color Color.Unspecified,fontSize: TextUnit TextUnit.Unspecified,fontStyle: FontStyle? null,fontWeight: FontWeight? null,fontFamily: FontFamily? null,letterSpac…...
动手学深度学习——Windows下的环境安装流程(一步一步安装,图文并配)
目录 环境安装官网步骤图文版安装Miniconda下载包含本书全部代码的压缩包使用conda创建虚拟(运行)环境使用conda创建虚拟环境并安装本书需要的软件激活之前创建的环境打开Jupyter记事本 环境安装 文章参考来源:http://t.csdn.cn/tu8V8 官网…...

打印日志遇到的问题,logback与zookeeper冲突
在做项目时需要打印日志引入了logback打印日志,但是一直无法打印,于是一路查找原因。发现zookeeper中默认带的有个logback和我自己引入的logback版本冲突了,这样直接使用exclusions标签将zookeeper中自带的日志框架全部排除即可 按理说到这一…...

【Node.js操作SQLite指南】
Node.js操作SQLite指南 在本篇博客中,我们将学习如何在Node.js中操作SQLite数据库。我们将使用sqlite3模块来创建数据库、创建表以及进行数据的增删改查操作。 文章目录 Node.js操作SQLite指南安装sqlite3模块创建数据库创建表数据的增删改查插入数据查询数据更新…...
PyTorch之张量的相关操作大全 ->(个人学习记录笔记)
文章目录 Torch1. 张量的创建1.1 直接创建1.1.1 torch.tensor1.1.2 torch.from_numpy(ndarray) 1.2 依据数值创建1.2.1 torch.zeros1.2.2 torch.zeros_like1.2.3 torch.ones1.2.4 torch.ones_like1.2.5 torch.full1.2.6 torch.full_like1.2.7 torch.arange1.2.8 torch.linspace…...

ChatGPT生成内容很难脱离标准化,不建议用来写留学文书
ChatGPT无疑是23年留学届的热门话题,也成为了不少留学生再也离不开的万能工具,从总结文献、润色论文、给教授写email似乎无所不能。 各大高校对于学生使用ChatGPT的态度也有所不同。例如,哈佛大学教育代理院长 Anne Harrington 在内部邮件中…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
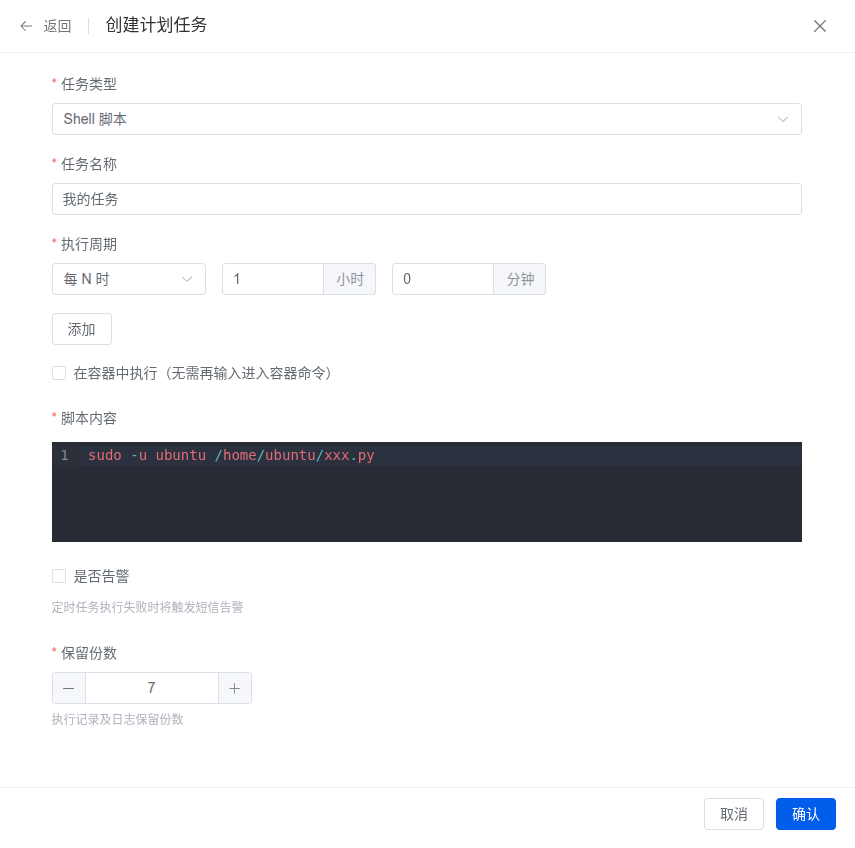
【Linux】使用1Panel 面板让服务器定时自动执行任务
服务器就是一台24小时开机的主机,相比自己家中不定时开关机的主机更适合完成定时任务,例如下载资源、备份上传,或者登录某个网站执行一些操作,只需要编写 脚本,然后让服务器定时来执行这个脚本就可以。 有很多方法实现…...
