二叉树oj题
目录
层序遍历(一)
题目
思路
代码
层序遍历(二)
题目
思路
代码
根据二叉树创建字符串
题目
思路
代码
二叉树的最近公共祖先
题目
思路
代码
暴力版
队列版
栈版
bs树和双向链表
题目
思路
代码
前序中序序列构建二叉树
题目
思路
代码
中序后序序列构建二叉树
题目
思路
代码
非递归前序遍历
题目
思路
代码
非递归中序遍历
题目
思路
代码
非递归后序遍历
题目
思路
代码
层序遍历(一)
题目
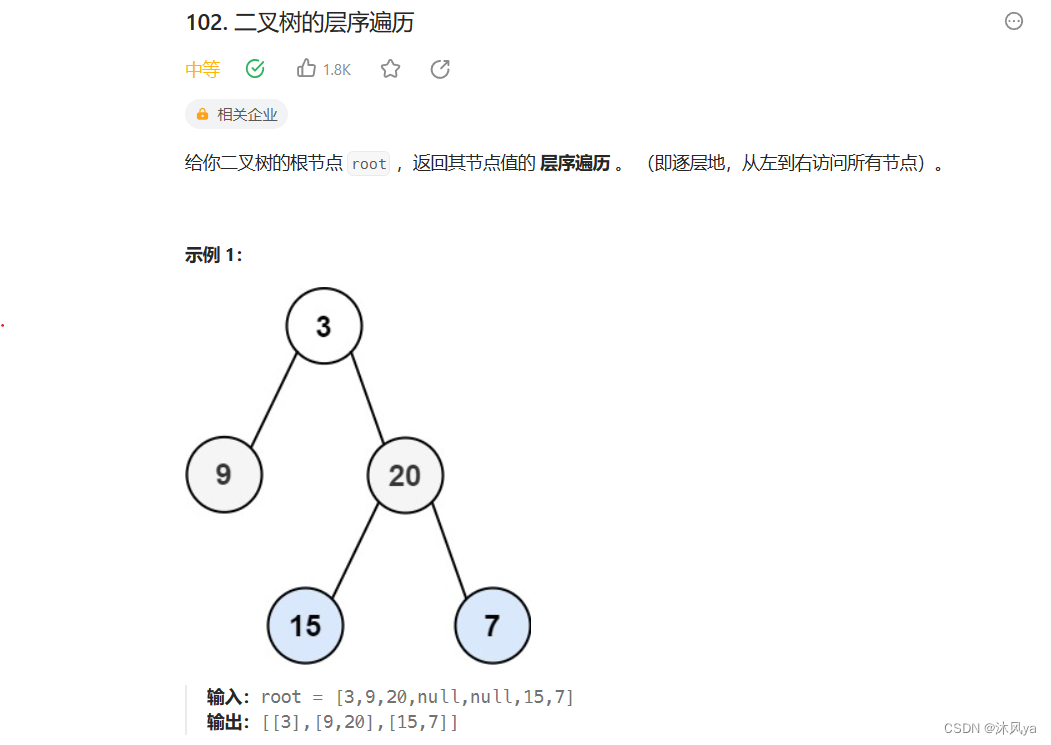
102. 二叉树的层序遍历 - 力扣(LeetCode)
思路
之前写过层序遍历,思路就是用队列存储结点,每次出一层,然后入出的结点的子结点
重点就是要记录一层的结点个数,然后出相应个数的结点
代码
vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> arr;queue<TreeNode*> q;if(root!=nullptr){q.push(root);}while(!q.empty()){vector<int> tmp; //存储一层的结点int size=q.size(); //此时队列内的元素就是上一层的结点个数for(int i=0;i<size;++i){tmp.push_back(q.front()->val);if(q.front()->left){ //有子树就放进队列中q.push(q.front()->left);}if(q.front()->right){q.push(q.front()->right);}q.pop(); //出掉这个父结点}arr.push_back(tmp);}return arr;}层序遍历(二)
题目
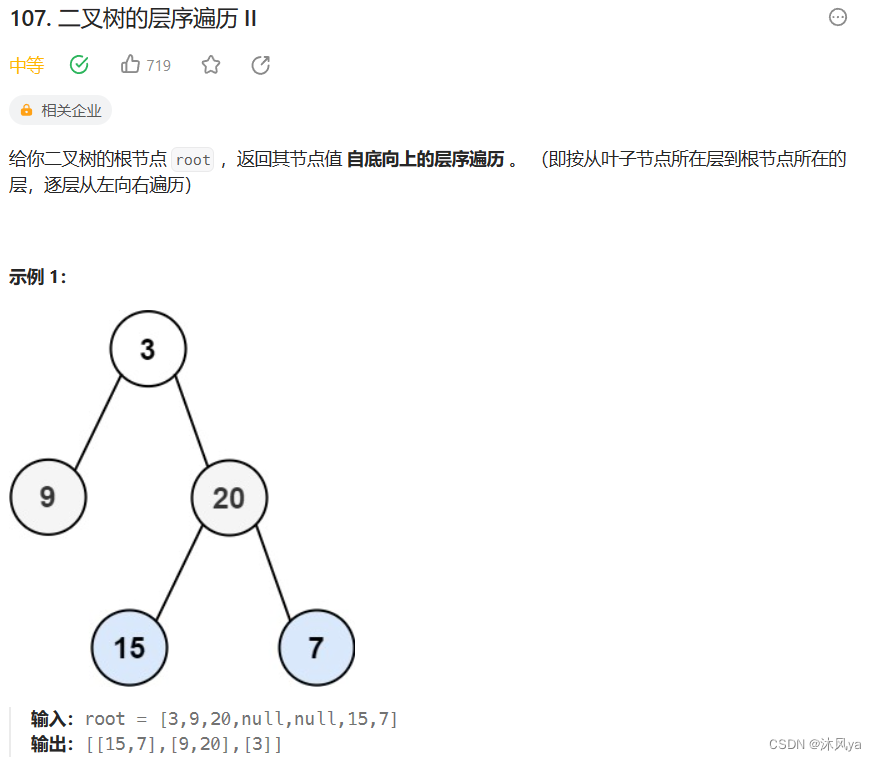
107. 二叉树的层序遍历 II - 力扣(LeetCode)
思路
看似好像很麻烦,其实只要把上一道题得到的答案逆置就行了
代码
vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> arr;queue<TreeNode*> q;if(root!=nullptr){q.push(root);}while(!q.empty()){vector<int> tmp;int size=q.size();for(int i=0;i<size;++i){tmp.push_back(q.front()->val);if(q.front()->left){q.push(q.front()->left);}if(q.front()->right){q.push(q.front()->right);}q.pop();}arr.push_back(tmp);}reverse(arr.begin(),arr.end()); //逆置return arr;}根据二叉树创建字符串
题目
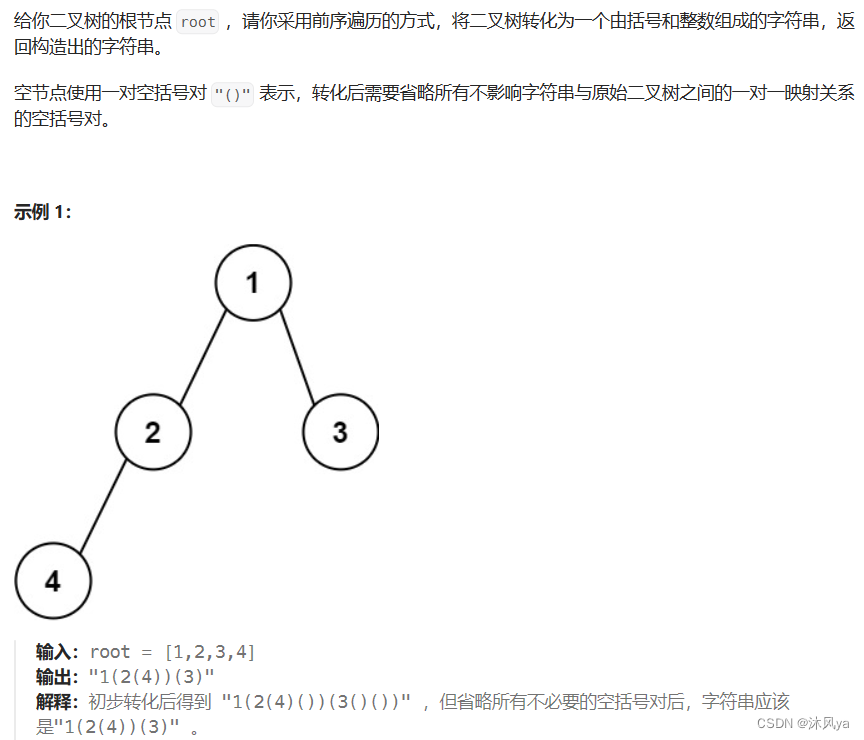
606. 根据二叉树创建字符串 - 力扣(LeetCode)
思路
基础代码还是一个前序遍历,只不过需要在打印时需要好好处理一下
- 首先,不能有不必要的括号,比如有左树无右树 / 左右子树全无
- 但是要注意,当无左树有右树时,需要将左树的空括号打印出来
代码
void front_order(TreeNode* root,string& ans){if(root==nullptr){return ;}ans+=to_string(root->val);if(root->left||root->right){ //左需要特殊判断,左右均有/只有右/只有左,都需要打印左,即使是空括号ans+='(';front_order(root->left,ans);ans+=')';}if(root->right){ //右只需要在它存在时打印ans+="(";front_order(root->right,ans);ans+=')';}}string tree2str(TreeNode* root) {string ans;front_order(root,ans);return ans;}二叉树的最近公共祖先
题目
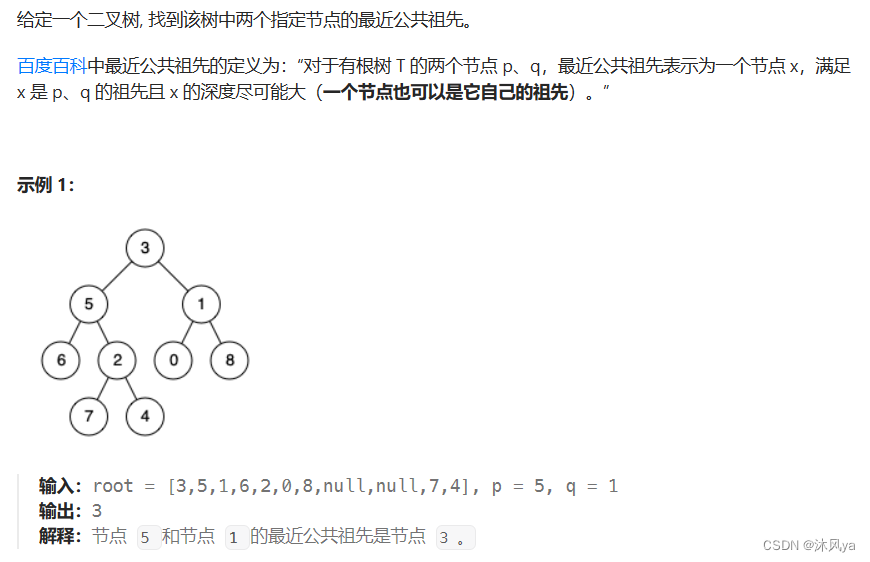
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
思路
- 如果要找的两个结点分别在某一结点的左右,说明该结点就是公共结点
- 如果两个结点都在某结点的左子树,那么该结点不会是公共结点,且确定公共结点需要在该结点的左子树中寻找 ; 右子树同理
- 如果某结点就是要找的两个结点的其中一个结点
除了直接找结点位置,也可以将结点路径存储起来,然后按照找相交链表的交点那样(先从尾巴出[相差个数]个结点),找出公共结点
队列/栈储存都是一样的
代码
暴力版
bool find(TreeNode* root, TreeNode* p){if(root==nullptr){return false;}if(root==p){return true;}return find(root->left,p)||find(root->right,p); //只要一边找到了就返回真}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==nullptr){return nullptr;}if(root==p||root==q){return root;}//判断当前结点下,要找结点的相对位置bool pleft=find(root->left,p);bool pright=!pleft;bool qleft=find(root->left,q);bool qright=!qleft;//如果都在左,去左找if(pleft&&qleft){return lowestCommonAncestor(root->left,p,q);}//如果都在右,去右找else if(pright&&qright){return lowestCommonAncestor(root->right,p,q);}//走到这里,说明一左一右else{return root;}}队列版
bool find_q(TreeNode* root, TreeNode* p,queue<TreeNode*>& ans){if(root==nullptr){return false;}if(root==p){ ans.push(root); //队列:先入子结点,保证先出的是子结点return true;}if(find_q(root->left,p,ans)){ //为真就存储起来(说明当前结点是路径上的一点)ans.push(root);return true;}if(find_q(root->right,p,ans)){ //同理ans.push(root);return true;} return false; //走到这里,说明左右均没找到,就说明这条路没有要找的结点}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {queue<TreeNode*> sp,sq;find_q(root,p,sp);find_q(root,q,sq);//先将多的出掉while(sp.size()>sq.size()){sp.pop();}while(sp.size()<sq.size()){sq.pop();}//然后同时出,直到找到那个公共结点while(sp.front()!=sq.front()){sp.pop();sq.pop();}return sp.front();}栈版
bool find_s(TreeNode* root, TreeNode* p,stack<TreeNode*>& ans){if(root==nullptr){return false;}ans.push(root); //注意:栈必须得先入父结点,保证先出的是子结点if(root==p){return true;}if(find_s(root->left,p,ans)){return true;}if(find_s(root->right,p,ans)){return true;}ans.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> sp,sq;find_s(root,p,sp);find_s(root,q,sq);while(sp.size()>sq.size()){sp.pop();}while(sp.size()<sq.size()){sq.pop();}while(sp.top()!=sq.top()){sp.pop();sq.pop();}}bs树和双向链表
题目
二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)
思路
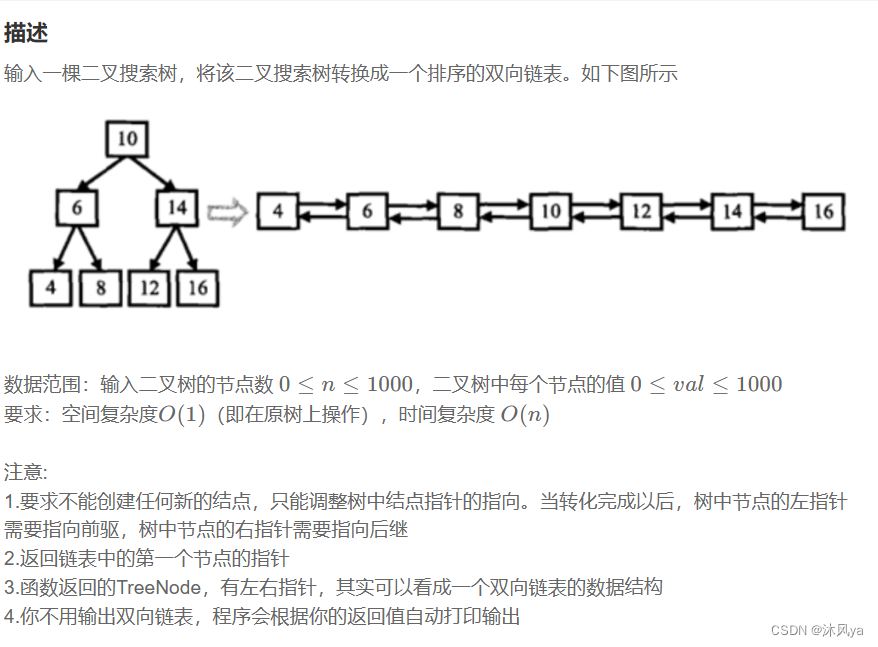
仔细看转化后的双向链表,结点顺序其实就是中序遍历的结点顺序
所以这道题的代码就是在中序遍历的基础上进行处理
- 因为需要指向前驱和后继,所以至少得搞一个变量,存上一个结点
- (毕竟没法知道下一个结点是啥,但上一个还是可以的,就像之前拿到父结点那样)
- 那么前驱搞定了,后继呢?
- 其实知道后继也可以,只要穿越到未来,再回到过去就可以知道了
- 所以,我们实际上知道的后继是上一个结点的,也就是当前结点 (当前结点就是上一个结点的后继)
- 还要注意一点,我们找到的第一个结点是最左端的,所以它没有前驱
- 所以首次传入的prev是空指针(prev赋值给结点的前驱)
代码
void inorder(TreeNode* root,TreeNode*& prev){if(root==nullptr){return;}inorder(root->left,prev);root->left=prev;if(prev){ //prev会为空,所以需要判断,不然就越界了prev->right=root;}prev=root; //因为之后要进root的后继结点了,所以需要更新previnorder(root->right,prev);}TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree==nullptr){return nullptr;}TreeNode *prev=nullptr,*tmp=pRootOfTree;while(tmp->left!=nullptr){ //拿到链表的第一个结点tmp=tmp->left;}inorder(pRootOfTree,prev);return tmp;}前序中序序列构建二叉树
题目
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
思路
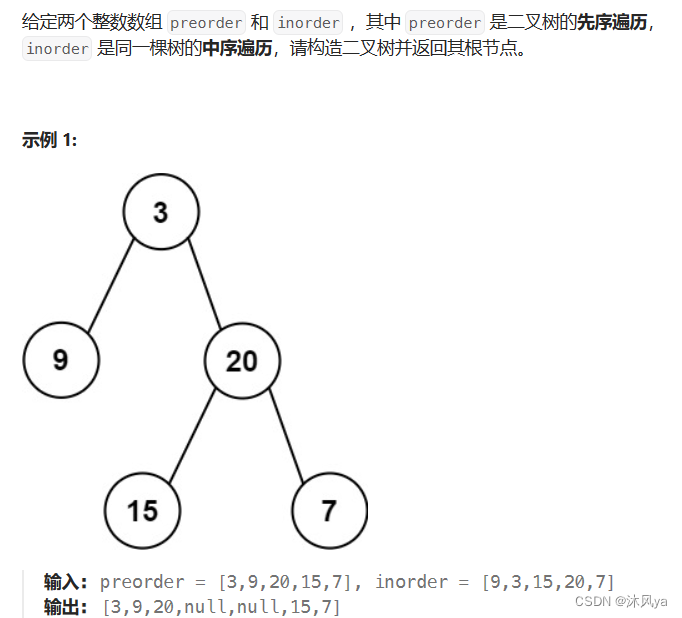
和手动构建树的顺序一样,前序确定根,中序确定根的左右子树,只不过需要用代码写出来
- 因为每次都需要将中序数组分成两个(是不是很像快排里面的操作),所以我们还是使用递归来写
- 但要注意,我们还需要一个不断增加的下标来访问前序(中序需要使用两个下标作为范围,它直接传值就行)
代码
class Solution {
public:TreeNode* _build(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend) {if (inbegin > inend) { //数组不合法,说明不存在这个结点,所以返回空return nullptr;}TreeNode* node = new TreeNode(preorder[prei]); //按照前序构建二叉树(因为先拿到的都是根结点)int begin = inbegin;// while(preorder[prei]!=inorder[begin]&&begin<=inend){// begin++;// }for (; begin <= inend; ++begin) { //在中序中找到根结点if (preorder[prei] == inorder[begin]) {break;}}++prei; //拿到下一个结点node->left = _build(preorder, inorder, prei, inbegin, begin - 1);//在找到的根结点,左区间是左子树node->right = _build(preorder, inorder, prei, begin + 1, inend);//同理return node;//左右子树构建完毕后,返回该结点}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int prei = 0, inbegin = 0, inend = inorder.size();TreeNode* root = _build(preorder, inorder, prei, 0, (int)inorder.size() - 1);//注意这里的prei是引用return root; //最后返回的就是根结点}
};中序后序序列构建二叉树
题目
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
思路
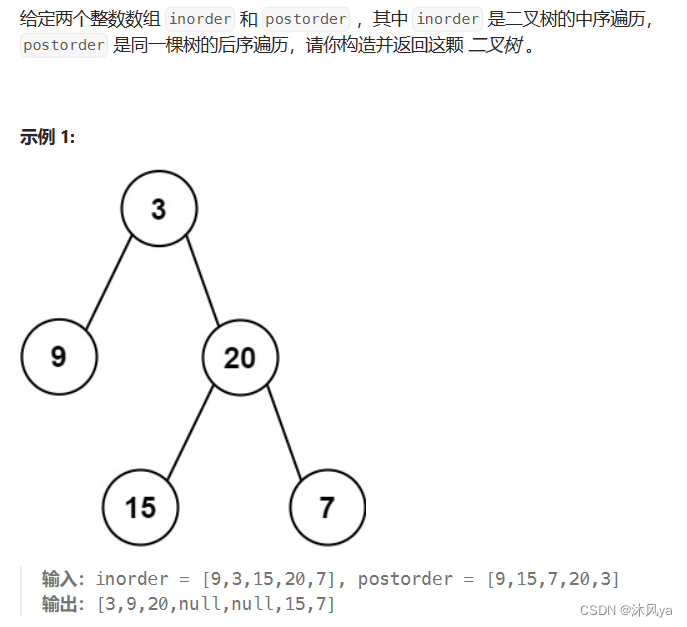
大体思路和上一道题一样,只不过是用后序找根
- 而且要注意后序是左右根的顺序
- 后序序列往左走,先找的是右子树的根,所以要先去中序的右半范围寻找
代码
TreeNode* _build(vector<int>& inorder, vector<int>& postorder,int& posti,int inbegin,int inend){if(inbegin>inend){return nullptr;}TreeNode* root=new TreeNode(postorder[posti]);int begin=inbegin;while(begin<=inend){if(postorder[posti]==inorder[begin]){break;}begin++;}--posti; //注意是--嗷root->right=_build(inorder,postorder,posti,begin+1,inend);//先被构建的是右子树root->left=_build(inorder,postorder,posti,inbegin,begin-1);return root;
}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int posti=postorder.size()-1;TreeNode* root=_build(inorder,postorder,posti,0,inorder.size()-1);return root;}非递归前序遍历
题目
144. 二叉树的前序遍历 - 力扣(LeetCode)
思路
虽然是非递归,但思路和递归一样,只不过得用循环做
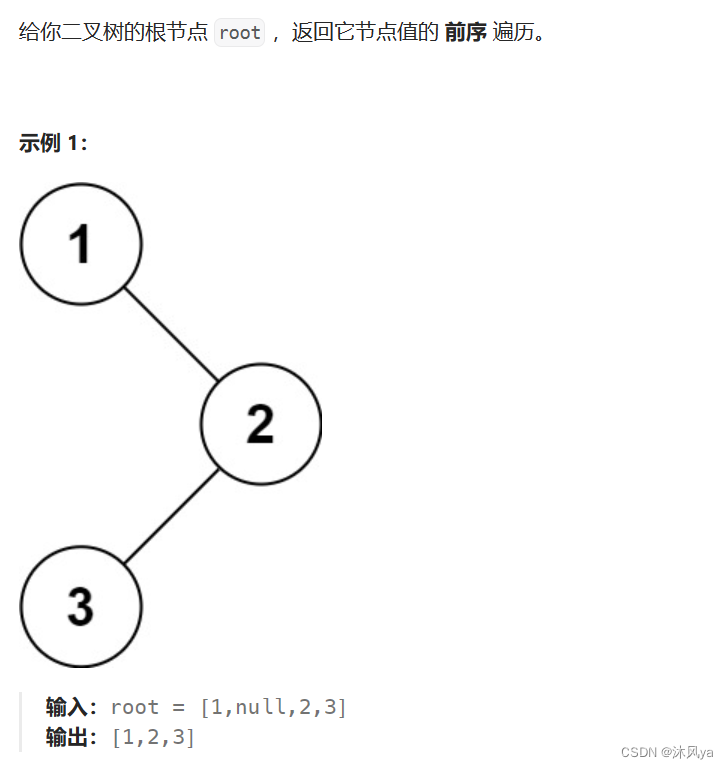
- 前序是根左右
- 也就是说,前序的前几个元素都是左方结点
- 之后开始访问右子树(按照左方节点的倒序)
- 所以,倒序 -- 不就是栈吗,先入后出!!
- 所以要用一个栈来存放左结点,然后不断取栈顶+访问其右子树
代码
vector<int> preorderTraversal(TreeNode* root) {vector<int> ans; //存放前序序列的结点值stack<TreeNode*> tmp; //存放左结点指针,用于访问其右子树TreeNode* cur=root;while(!tmp.empty()||cur){ //栈空+当前结点是空结点,出循环while(cur){ans.push_back(cur->val); //入左结点tmp.push(cur); //存左结点指针cur=cur->left;}TreeNode* top=tmp.top(); cur=top->right; //访问右子树tmp.pop();}return ans;}非递归中序遍历
题目
94. 二叉树的中序遍历 - 力扣(LeetCode)
思路
和前序的思路差不多,但是要注意,中序是左根右
- 所以需要将左结点先存入栈中(先不要访问!!!)
- 然后按照栈中顺序,取出,访问
- 然后,将拿出结点的右结点按照上述操作重复进行,直到遍历完整棵树
代码
vector<int> inorderTraversal(TreeNode* root) {vector<int> ans; //存放中序序列的结点值stack<TreeNode*> tmp; //存放左结点指针,用于访问其右子树TreeNode* cur=root;while(!tmp.empty()||cur){ //栈空+当前结点是空结点,出循环while(cur){ //把所有左结点入栈tmp.push(cur);cur=cur->left;}cur=tmp.top(); //拿取栈顶元素ans.push_back(cur->val); //入中序序列cur=cur->right; //访问其右子树tmp.pop(); //该结点没啥用了,直接出}return ans;}非递归后序遍历
题目
145. 二叉树的后序遍历 - 力扣(LeetCode)
思路
- 后序是左右根
- 也就是说,要先遍历完左结点,以及右结点后,才能访问结点
- 而且要注意,如果该结点有右子树,就需要先循环右子树
- 但是当循环完成后需要返回来访问结点
- 该如何判断此时到底该访问右子树还是访问自己呢?
- 想一想,当上一个结点是其右结点时,不就是该访问自己的时候吗?
- 而上一个结点是左结点时,是该访问右子树的时候了
- 所以需要拿到父结点,然后进行判断
代码
vector<int> postorderTraversal(TreeNode* root) {vector<int> ans; //存放中序序列的结点值stack<TreeNode*> tmp; //存放左结点指针,用于访问其右子树TreeNode* cur=root,*prev=nullptr; while(!tmp.empty()||cur){ //栈空+当前结点是空结点,出循环while(cur){ //把所有左结点入栈(cur就用于把当前结点的左结点存入栈)tmp.push(cur); cur=cur->left;}TreeNode* top=tmp.top(); //代表当前的根结点if(top->right==nullptr || top->right==prev){ans.push_back(top->val); //入后序序列prev=top; //用于下一次循环时,判断上一个结点的右子树是否被访问过tmp.pop(); //该结点没啥用了,直接出}else{cur=top->right; //没有被访问过,就去右子树进行循环}}return ans;}相关文章:
二叉树oj题
目录 层序遍历(一) 题目 思路 代码 层序遍历(二) 题目 思路 代码 根据二叉树创建字符串 题目 思路 代码 二叉树的最近公共祖先 题目 思路 代码 暴力版 队列版 栈版 bs树和双向链表 题目 思路 代码 前序中序序列构建二叉树 题目 思路 代码 中序后序…...

华为数通方向HCIP-DataCom H12-831题库(单选题:1-20)
第1题 关于IPSG下列说法错误的是? A、IPSG可以防范IP地址欺骗攻击 B、IPSG是一种基于三层接口的源IP地址过滤技术 C、IPSG可以开启IP报文检查告警功能,联动网管进行告警 D、可以通过IPSG防止主机私自更改IP地址 答案: B 解析: IPSG(入侵防护系统)并不是基于三层接口的源I…...

TableConvert-免费在线表格转工具 让表格转换变得更容易
在线表格转工具TableConvert TableConvert 是一个基于web的免费且强大在线表格转换工具,它可以在 Excel、CSV、LaTeX 表格、HTML、JSON 数组、insert SQL、Markdown 表格 和 MediaWiki 表格等之间进行互相转换,也可以通过在线表格编辑器轻松的创建和生成…...

伦敦金实时行情中的震荡
不知道各位伦敦金投资者,曾经花过多长的时间来观察行情走势的表现,不知道大家是否有统计过,其实行情有60%-70%的时间,都会处于没有明显方向的震荡行情之中呢?面对长期的震荡行情,伦敦金投资者道理应该如何应…...

蓝桥杯打卡Day7
文章目录 阶乘的末尾0整除问题 一、阶乘的末尾0IO链接 本题思路:由于本题需要求阶乘的末尾0,由于我们知道2*510可以得到一个0,那么我们就可以找出2的数和5的数,但是由于是阶乘,所以5的数量肯定是小于2的数量…...
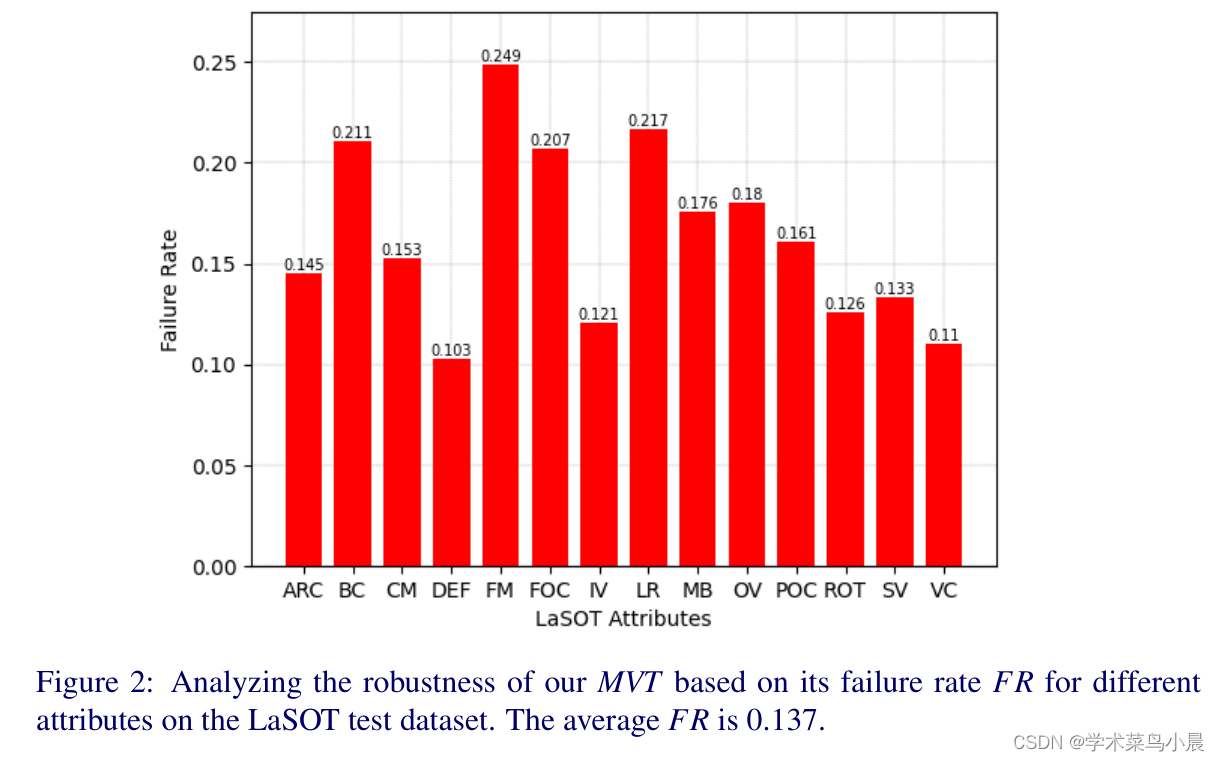
Mobile Vision Transformer-based Visual Object Tracking
论文作者:Goutam Yelluru Gopal,Maria A. Amer 作者单位:Concordia University 论文链接:https://arxiv.org/pdf/2309.05829v1.pdf 项目链接:https://github.com/goutamyg/MVT 内容简介: 1)方向&#…...

HTTP反爬困境
尊敬的程序员朋友们,大家好!今天我要和您分享一篇关于解决反爬困境的文章。在网络爬虫的时代,许多网站采取了反爬措施来保护自己的数据资源。然而,作为程序员,我们有着聪明才智和技术能力,可以应对这些困境…...
----函数指针与回调函数)
从零开始探索C语言(九)----函数指针与回调函数
函数指针 函数指针是指向函数的指针变量。 通常我们说的指针变量是指向一个整型、字符型或数组等变量,而函数指针是指向函数。 函数指针可以像一般函数一样,用于调用函数、传递参数。 函数指针变量的声明: typedef int (*fun_ptr)(int,i…...

智慧工厂的基础是什么?功能有哪些?
关键词:智慧工厂、智慧工厂数字化、设备设施数字化、智能运维、工业互联网 1.智慧工厂的定义 智慧工厂是以数字化信息形式的工厂模型为基础,以实现制造系统离线分析设计和实际生产系统运行状态在线监控的新型工厂。智慧工厂的建设在于以高度集成的信息化…...

LeetCode 238. 除自身以外数组的乘积
题目链接 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目解析 使用前缀和进行解决该题,只不过与之前前缀和不同的是这个题目计算前缀和的时候不需要计算当前元素,也就是当前位置前缀和的值其实是不包含当前元素的前缀和。…...

点击劫持概念及解决办法
1.点击劫持的概念 点击劫持 (Clickjacking) 技术又称为界面伪装攻击 (UI redress attack ),是一种视觉上的欺骗手段。攻击者使用一个或多个透明的 iframe 覆盖在一个正常的网页上,然后诱使用户在该网页上进行操作,当用户在不知情的情况下点击…...
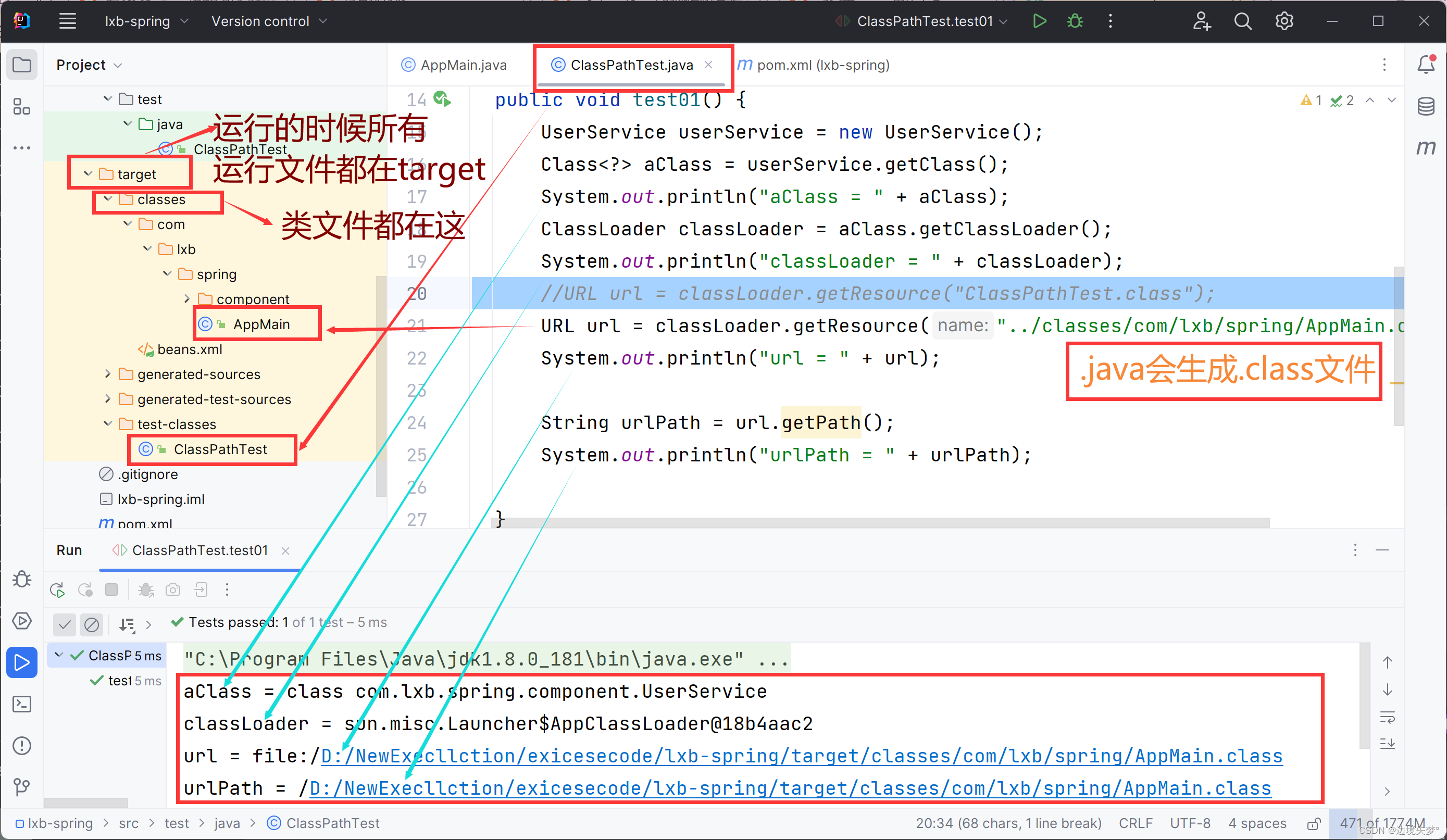
【Spring】手动实现Spring底层机制-问题的引出
🎄欢迎来到边境矢梦的csdn博文🎄 🎄本文主要梳理手动实现Spring底层机制-问题的引出 🎄 🌈我是边境矢梦,一个正在为秋招和算法竞赛做准备的学生🌈 🎆喜欢的朋友可以关注一下…...

Java - List 去重,获取唯一值,分组列出所属对应集合
问题:List 去重,获取唯一值,分组列出所属对应集合 方案一:这个不需要额外的内存占用 //遍历后判断赋给另一个list集合public static void main(String[] args){List<String> list new ArrayList<String>(); lis…...
)
离散高斯抽样(Discrete Gaussian Sampling)
离散高斯抽样 离散高斯抽样(Discrete Gaussian Sampling)是一种常见于密码学和数学领域的随机采样方法。它通常用于构建基于格(lattice)的密码学方案,如基于格的加密和数字签名。Discrete Gaussian Sampling 的主要目…...
Elasticsearch:什么是生成式人工智能?
生成式人工智能定义 给学生的解释(基本): 生成式人工智能是一种可以创造新的原创内容的技术,例如艺术、音乐、软件代码和写作。 当用户输入提示时,人工智能会根据从互联网上现有示例中学到的知识生成响应,…...
责任链模式让我的代码精简10倍?
目录 什么是责任链使用场景结语 前言最近,我让团队内一位成员写了一个导入功能。他使用了责任链模式,代码堆的非常多,bug 也多,没有达到我预期的效果。实际上,针对导入功能,我认为模版方法更合适ÿ…...
Draw软件安装下载
Draw软件安装下载 1.软件简介2.软件下载3.安装方法 1.软件简介 Draw软件,全名为LibreOffice Draw,是一款免费、开源的2D矢量绘图软件,属于LibreOffice办公套件的一部分。它可以用来创建各种类型的图形,包括流程图、组织结构图、平…...

uniapp代码混淆ios上架43问题
参考文章:uniapp打包ios apk,混淆代码_uniapp 混淆_酸奶自由竟然重名了的博客-CSDN博客 uniapp打包ios,上传到ios应用市场时,会因为 4.3(代码重复率过高) 无法通过审核,此时可通过混淆代码来通过审核 1. 项目终端 安…...

Linux目录遍历函数
1.打开一个目录 #include <sys/types.h> #include <dirent.h> DIR *opendir(const char *name); 参数: -name:需要打开的目录的名称 返回值: DIR * 类型,理解为目录流 错误返回NULL 2.读取目录中的数据 #include <dirent.h…...

数据库-理论基础
目录 1.什么是数据库? 2.数据库与文件系统的区别? 3.常见的数据库由那些? 4.关系型数据库(MySQL)的特征及组成结构介绍 1.什么是数据库? 数据:描述事物的符号记录,可以是数字,文…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...