线性代数(六) 线性变换
前言
《线性空间》定义了空间,这章节来研究空间与空间的关联性
函数
函数是一个规则或映射,将一个集合中的每个元素(称为自变量)映射到另一个集合中的唯一元素(称为因变量)。

一般函数从 “A” 的每个元素指向 “B” 的一个函数
它不会有一个 “A” 的元素指向多于一个 “B” 的元素,所以一对多在函数是不允许的(“f(x) = 7 或 9” 是不允许的)
但多于一个 “A” 的元素可以指向同一个 “B” 的元素(多对一是允许的)
- 单射的意思是 “A” 的每个元素都有 它独有的在 “B” 的相对元素。单射也称为 “一对一”。但可以有些 “B” 的元素没有相对的 “A” 的元素。单射存在可逆函数,使得B对A单射
- 满射,每个(所有) “B” 的元素都有至少一个相对的 “A” 的元素(可能多于一个)。
- 双射,单射和满射都成立。
线性空间的同构

- 同构映射具有反身性、对称性与传递性。
- 内积空间同构,还需要满足内积不变, ∀ α , β ∈ V , 有 ( σ ( α ) , σ ( β ) ) = ( α , β ) \forall \alpha,\beta \in V, 有(\sigma(\alpha),\sigma(\beta)) = (\alpha, \beta) ∀α,β∈V,有(σ(α),σ(β))=(α,β)
使用单射,满射满足性线空间性质的称为同态(了解下)
线性变换
把上述同构定义中的 V ′ V' V′换成 V V V,即 V V V空间通过双射函数到 V V V空间的映射。称为“自同构”。如果是“单射”或者“满射”函数映射,则称为“自同态”。也称叫“线性变换”。
线性变换(linear transformation)是线性空间V到其自身的线性映射
线性变换的矩阵

从公式可得,因为最终值是不变的,如果基组选取不同,A矩阵会变动
线性变换不同基下的矩阵
由上面的关系式可以看出,若选定不同的基,则同一个线性变换在不同基下面的矩阵是不同的,但是这两个矩阵之间存在着一种特殊的关系

矩阵 A A A和矩阵 B B B 之间的这种关系为相似关系,即同一个线性变换在不同基下的矩阵是相似的。即有相似矩阵的性质
矩阵的相似对角化
上面讲述了线性变换在不同基下的矩阵之间的关系,知道了线性变换在不同基下的矩阵是相似的。进而我们可以通过选取不同的基,使得线性变换在这组基下的矩阵的形式最简单,由于对角矩阵具有良好的性质,因此我们希望通过选取合适的基,使得线性变换在这组基下的矩阵是对角矩阵。怎么找到对角矩阵 Λ \Lambda Λ?
Λ = P − 1 A P \Lambda = P^{-1}AP Λ=P−1AP
A是已知 φ \varphi φ,问题等价于寻找一个可逆矩阵P

反过来,若 A A A是可相似对角化,那么 A A A是否有n个线性无关的特征向量呢?

综上,矩阵 A A A可相似对角化的充分必要条件是矩阵 A A A有n个线性无关的特征向量

求相似对角化矩阵
- 已知: Λ = P − 1 A P , { ε } P = { η } \Lambda = P^{-1}AP, \{\varepsilon\}P = \{\eta\} Λ=P−1AP,{ε}P={η}, P是过渡矩阵
- 假设 { ε } \{\varepsilon\} {ε}是欧式空间的标准正交基组,已矩阵A
- 验证充分必要条件:矩阵 A A A有n个线性无关的特征向量
- 将n个线性无关的特征向量,组建新的基组{ β \beta β}
- 为了更方便的计算,我们将基组{ β \beta β},施密特正交化,求出标准正交基本组{ η \eta η}
- 根据 { ε } P = { η } \{\varepsilon\}P = \{\eta\} {ε}P={η}得 P = { η } P=\{\eta\} P={η}
- 代入公式 Λ = P − 1 A P \Lambda = P^{-1}AP Λ=P−1AP,得对角矩阵 Λ \Lambda Λ
具体计算过程:实对称矩阵的对角化
对于n维线性空间V上的线性变换A,如果能够找到一个基{ a 1 , a 2 , . . . a n a_1,a_2,...a_n a1,a2,...an}使得在此基下的矩阵A是对角矩阵,那么称A是可对角化。但是如果A不能对角化呢?我们便退而求其次,找到一个基{ a 1 , a 2 , . . . a n a_1,a_2,...a_n a1,a2,...an}使得在此基下的矩阵A是分块对角矩阵。
不变子空间

A \Alpha A是线性变换
- Im A \operatorname{Im} A ImA 是指线性变换 A 的值域(Image),也被称为像空间或范围。它表示所有通过该线性变换 A 映射到的向量的集合。
- Ker A \operatorname{Ker} A KerA是指线性变换A的核空间(Kernel),也被称为零空间(Null Space)。它表示所有在该线性变换下映射到零向量的向量的集合。
- A的特征子空间(Eigenspace)是指在线性变换A下与给定特征值 λ {\lambda} λ相对应的所有特征向量构成的子空间 V λ {V_\lambda} Vλ。
一些重要不变子空间
-
Im A \operatorname{Im} A ImA或V空间本身
- 任取 a ∈ V , A a ∈ V a \in V, Aa \in V a∈V,Aa∈V
- A a ∈ Im A , A ( A a ) ∈ Im A Aa \in \operatorname{Im} A, A(Aa) \in \operatorname{Im} A Aa∈ImA,A(Aa)∈ImA
-
Ker A \operatorname{Ker} A KerA或0空间
-
A的特征子空间
假设V在A线性变化下,有一特征值为 λ {\lambda} λ,对应特征向量组成的空间为A的特征子空间,记 V λ {V_\lambda} Vλ.
- 任取 a ∈ V λ , A a = λ a ∈ V λ a \in V_{\lambda},Aa=\lambda a \in V_{\lambda} a∈Vλ,Aa=λa∈Vλ
-
设B也是V上的线性变换,如果A和B可交换,那么 Im B , Ker B , B \operatorname{Im} B,\operatorname{Ker} B,B ImB,KerB,B的特征子空间 是A-子空间

-
V上的线性变换A的不变子空间的和与交仍是A的不变子空间.
- a ∈ A 1 − , b ∈ A 2 − , a + b ∈ A 1 − ⊕ A 2 − a \in A_1-, b \in A_2-, a+b \in A_1- \oplus A_2- a∈A1−,b∈A2−,a+b∈A1−⊕A2−
- A ( a + b ) = A a + A b ∈ A − ⊕ B − A(a+b) = Aa + Ab \in A- \oplus B- A(a+b)=Aa+Ab∈A−⊕B−
-

线性变换在不变子空间上的限制

不变子空间与线性变换的矩阵化简

把基本不变子空间W分成 ( ε w , ε o t h r e r ) (\varepsilon_w,\varepsilon_{othrer}) (εw,εothrer),又因为 A 1 A_1 A1是W的线性变化,在 ε w \varepsilon_w εw下必是 ε w A 1 \varepsilon_wA_1 εwA1.即当仅仅当矩阵满足以下形状
( A 1 A 2 0 A 3 ) \begin{pmatrix} A_1 & A_2\\ 0 & A_{3} \end{pmatrix} (A10A2A3)
才能满足需求。

即:V的线性变换A可分块对角矩阵化的充要条件是 V可分解为A的不变子空间的直和
Hamilton-Cayley定理与值和分解

即将特征多项式
f ( λ ) = | λ I − A ∣ f(\lambda)=|\lambda I-A| f(λ)=|λI−A∣
再根据多项式因式分解得
f ( λ ) = f 1 ( λ ) f 2 ( λ ) . . . f n ( λ ) = 0 f(\lambda)=f_1(\lambda)f_2(\lambda)...f_n(\lambda) = 0 f(λ)=f1(λ)f2(λ)...fn(λ)=0
其中 f 1 ( λ ) f 2 ( λ ) . . . f n ( λ ) f_1(\lambda)f_2(\lambda)...f_n(\lambda) f1(λ)f2(λ)...fn(λ)互为素数
V = Ker f ( λ ) = Ker f 1 ( λ ) ⨁ Ker f 2 ( λ ) ⨁ . . . ⨁ Ker f n ( λ ) V=\operatorname{Ker}f(\lambda)=\operatorname{Ker}f_1(\lambda) \bigoplus \operatorname{Ker}f_2(\lambda)\bigoplus...\bigoplus\operatorname{Ker}f_n(\lambda) V=Kerf(λ)=Kerf1(λ)⨁Kerf2(λ)⨁...⨁Kerfn(λ)
将 f ( λ ) f(\lambda) f(λ)进一步分解
f ( λ ) = ( λ − λ 1 ) r 1 ( λ − λ 2 ) r 2 . . . ( λ − λ n ) r n f(\lambda)=(\lambda-\lambda_1)^{r_1}(\lambda-\lambda_2)^{r_2}...(\lambda-\lambda_n)^{r_n} f(λ)=(λ−λ1)r1(λ−λ2)r2...(λ−λn)rn
再线性变换A代入得
V = Ker ( ( A − λ 1 I ) r 1 ) ⨁ Ker ( ( A − λ 2 I ) r 2 ) ⨁ . . . ⨁ Ker ( ( A − λ n I ) r n ) V=\operatorname{Ker}((A-\lambda_1 I)^{r_1}) \bigoplus \operatorname{Ker}((A-\lambda_2I)^{r_2})\bigoplus...\bigoplus\operatorname{Ker}((A-\lambda_n I)^{r_n}) V=Ker((A−λ1I)r1)⨁Ker((A−λ2I)r2)⨁...⨁Ker((A−λnI)rn)
其中 Ker ( ( A − λ n I ) r n ) , n = 1 , 2... s \operatorname{Ker}((A-\lambda_n I)^{r_n}), n=1,2...s Ker((A−λnI)rn),n=1,2...s,称为根子空间
对角矩阵中的每个分块矩阵,对应着不同特征值 λ \lambda λ对应的空间
λ矩阵
所谓 λ \lambda λ矩阵,实际上我们并不陌生,在学习线性变换的特征值与特征向量时,我们引入了线性变换的特征矩阵 λ E − A \lambda E-A λE−A , 其中 A A A是数域 P P P上的n维线性空间 V V V中的线性变换 A A A 在某一组基 ε 1 , ε 2 , . . . ε 3 \varepsilon_1,\varepsilon_2,...\varepsilon_3 ε1,ε2,...ε3下的矩阵,这个特征矩阵 λ E − A \lambda E-A λE−A 就是一个 λ \lambda λ矩阵.

在我们学习数字矩阵时,矩阵当中的每一个位置都放置一个数字元素,而如果将数字矩阵当中的数字全部替换成数域 P P P上的一元多项式环 P [ λ ] P[\lambda] P[λ]中的一元多项式 f ( λ ) f(\lambda) f(λ),那么对应得到的新的矩阵就称之为 λ \lambda λ矩阵.
关于一元多项式环,请参考《补充P4关于环的知识》
- 由于一元多项式环 P [ λ ] P[\lambda] P[λ]中的多项式之间的运算——加法、减法、乘法与数字之间的加、减、乘遵循同样的运算规律,因此,对于 λ \lambda λ矩阵我们可以类似的定义 λ \lambda λ矩阵之间的加法、数乘以及乘法,这些运算与数字矩阵具有完全相同的运算规律。、
- 以定义 n × n n × n n×n的 λ \lambda λ矩阵.所对应的行列式,它与数字矩阵的行列式具有完全相同的性质. 矩阵乘积的行列式等于行列式的乘积,这一结论同样是成立的
- λ \lambda λ矩阵.的子式的概念,其与数字矩阵的子式的概念也是完全类似的

- λ \lambda λ矩阵可逆的定义与数字矩阵中的可逆的矩阵的定义是类似的

- λ \lambda λ矩阵可逆条件是 ∣ A ( λ ) ∣ = d |A(\lambda)|=d ∣A(λ)∣=d

λ \lambda λ矩阵的初等行列变换
- 互换矩阵中任意两行(列)的位置;
- 将矩阵中的任意一行(列)乘以一个非零常数;
- 将矩阵的任意一行(列)乘以任意 φ ( λ ) \varphi(\lambda) φ(λ)后加到另外一行(列)上。

在数字矩阵中,如果两个数字矩阵 A A A和 B B B 可以经过初等变换互化,那么我们称这两个矩阵是等价的,同样的我们也可以定义 λ \lambda λ矩阵的等价的概念。

标准型
λ \lambda λ矩阵在进行初等变换后能够将矩阵化简成简单标准的模型。


有了上面的引理,我们就可以得到下面的重要定理。

- 对于正整数 k k k, 1 ≤ k ≤ r 1\leq k \leq r 1≤k≤r, A ( λ ) A(\lambda) A(λ)中必有非零的 k k k级子式, A ( λ ) A(\lambda) A(λ) 中全部 k k k级子式的首项系数为1的最大公因式 D k ( λ ) D_k(\lambda) Dk(λ)称为 A ( λ ) A(\lambda) A(λ)的 k k k级行列式因子。
- 等价的 λ \lambda λ矩阵具有相同的秩与相同的各级行列式因子
这种最简单的矩阵称为 A ( λ ) A(\lambda) A(λ)的标准形,且是唯一的。


两个 λ \lambda λ矩阵等价的充要条件是它们有相同的行列式因子,或者它们有相同的不变因子
初等因子
初等因子,就是组成不变因子的“砖块”:如果不变因子 d k ( λ ) = ( λ − 1 ) 2 ( λ − 1 ) d_k(\lambda)=(\lambda-1)^2(\lambda-1) dk(λ)=(λ−1)2(λ−1) ,对应的初等因子就是 ( λ − 1 ) 2 、 ( λ − 1 ) (\lambda-1)^2、(\lambda-1) (λ−1)2、(λ−1).

标准型的可逆条件

同样相似矩阵的性质也适用 λ \lambda λ矩阵:
- A A A与 B B B 相似的充要条件是它们的特征矩阵 λ E − A \lambda E-A λE−A与 λ E − B \lambda E-B λE−B等价。
- 相似 A A A与 B B B ⟺ \iff ⟺有相同的不变因子 ⟺ \iff ⟺有相同的初等因子
若尔当(Jordan)标准形
Jordan标准形即分块对角阵

矩阵的若尔当标准形是为了解决那些不可相似对角化的矩阵的化简问题,我们知道,如果一个矩阵可以进行相似对角化,那么这个矩阵的一些运算就可以被极大的简化,由于相似矩阵之间具有很多的相似不变量:特征多项式、特征值、矩阵的行列式、矩阵的迹、最小多项式、不变因子、行列式因子、初等因子。因此如果一个矩阵能够相似一个形式简单的矩阵,那么在求上述相似不变量时就可以很容易的得到。

- 诺尔当块 J 0 J_0 J0的初等因子只有 ( λ − λ 0 ) n (\lambda-\lambda_0)^n (λ−λ0)n(其中的 λ 0 \lambda_0 λ0就是对角线上的元素)

- 诺尔当块 J 1 , J 2 , . . . J x J_1,J_2,...J_x J1,J2,...Jx的初等因子分别为 ( λ − λ 1 ) k 1 , ( λ − λ 2 ) k 2 , . . . , ( λ − λ s ) k s (\lambda-\lambda_1)^{k_1},(\lambda-\lambda_2)^{k_2},...,(\lambda-\lambda_s)^{k_s} (λ−λ1)k1,(λ−λ2)k2,...,(λ−λs)ks,它们组合起来的诺尔当型 J J J的初等因子,即是每个块的对角线元素 λ 0 \lambda_0 λ0与阶数 k i k_i ki的组合

于是,每个拥相同的初等因子的矩阵就都相似于 J J J,对于任意的矩阵 A A A ,它的特征矩阵 λ E − A \lambda E-A λE−A ,得到其初等因子为 ( λ − λ 1 ) k 1 , ( λ − λ 2 ) k 2 , . . . , ( λ − λ s ) k s (\lambda-\lambda_1)^{k_1},(\lambda-\lambda_2)^{k_2},...,(\lambda-\lambda_s)^{k_s} (λ−λ1)k1,(λ−λ2)k2,...,(λ−λs)ks.

主要参考
《单射、满射和双射》
《高等代数】线性空间的同构》
《线性同构与欧氏空间同构》
《什么是矩阵对角化》
《浅谈线性变换和矩阵之间的关系》
《浅谈矩阵的相似对角化(一)》
《线性代数(实对称矩阵的对角化)》
《不变子空间》
《【高等代数(丘维声著)笔记】6.8线性变换的不变子空间》
《补充P4关于环的知识》
《矩阵的初等变换》
《浅谈λ—矩阵与矩阵的若尔当标准形》
《laji高代题纲——λ-矩阵》
相关文章:

线性代数(六) 线性变换
前言 《线性空间》定义了空间,这章节来研究空间与空间的关联性 函数 函数是一个规则或映射,将一个集合中的每个元素(称为自变量)映射到另一个集合中的唯一元素(称为因变量)。 一般函数从 “A” 的每个元…...

Python基础运算分享
Python的运算符和其他语言类似 (我们暂时只了解这些运算符的基本用法,方便我们展开后面的内容,高级应用暂时不介绍) 数学运算 >>>print 19 # 加法>>>print 1.3-4 # 减法>>>print 3*5 …...
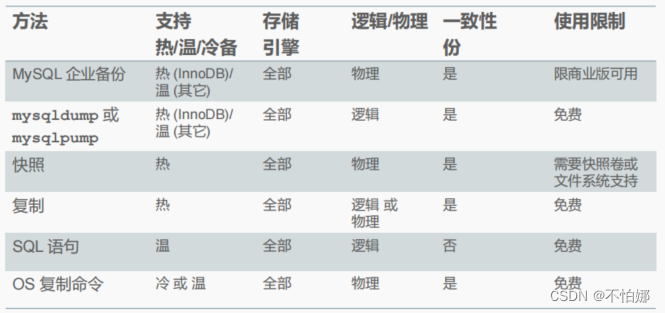
【MySQL】mysql中有哪几种类型的备份技术?它们各自有什么优缺点?
为什么要备份?备份类型(从类型的角度)备份技术(从技术手段的角度)不同备份方法的比较感谢 💖 为什么要备份? 数据库或它所在的平台可能会出现问题,这时候数据库中的数据可能就遭到了…...

5基于pytorch的多目标粒子群算法,MOPSO,引导种群逼近真实Pareto前沿,算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。
基于pytorch的多目标粒子群算法,MOPSO,引导种群逼近真实Pareto前沿,算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。程序已调通,可以直接运行。 5pytorch多目标粒子群算法最优解5pytorch多目标粒子群算法最优解 (xiaohongshu.co…...

002 Linux 权限
前言 本文将会向您介绍关于linux权限方面的内容,包括文件类型,如何切换用户、基本权限、粘滞位等等 Linux具体的用户 超级用户:可以再linux系统下做任何事情,不受限制 普通用户:在linux下做有限的事情。 超级用户的…...

【Java 基础篇】Java可变参数:灵活处理不定数量的方法参数
在Java编程中,可变参数是一项强大的功能,它允许你编写更加灵活的方法,接受不定数量的参数。本文将详细解释Java可变参数的用法、语法以及最佳实践。 什么是可变参数? 可变参数是Java 5引入的一项功能,它允许你在方法…...

“网站建设流程详解:从概念到上线的每个细节“
以下是网站建设流程的详细步骤,从概念到上线的每个细节: 确定网站目标和定位:明确网站的主题和目标,根据目标受众和市场定位来决定网站的内容和设计风格。考虑网站的目的、目标受众、行业或领域等方面,以及网站的定位…...

DC/DC开关电源学习笔记(七)低压大电流DC/DC变换技术
低压大电流DC/DC变换技术 1. 无暂态要求的低压大电流DC/DC变换技术2. 负载极其快速变化的低压大电流DC/DC变换技术2.1 非隔离型 VRM2.2 隔离型VRM低压大电流高功率 DC/DC 变换技术,已从前些年的 3.3V 降至现在的 1.0V 左右,电流目前已可达到几十安至几百安。同时,电源的输出指标…...

XUbuntu22.04之查找进程号pidof、pgrep总结(一百九十)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

BI与数据治理以及数据仓库有什么区别
你可能已经听说过BI、数据治理和数据仓库这些术语,它们在现代企业中起着重要的作用。虽然它们都与数据相关,但它们之间有着明显的区别和各自独特的功能。数聚将详细探讨BI(商业智能)、数据治理和数据仓库之间的区别,帮…...

java---jar详解
一、help C:\Users\lichf1>jar 用法: jar {ctxui}[vfmn0PMe] [jar-file] [manifest-file] [entry-point] [-C dir] files ... 选项:-c 创建新档案-t 列出档案目录-x 从档案中提取指定的 (或所有) 文件-u 更新现有档案-v 在标准输出中生成详细输出-f 指定档案文件名-m…...
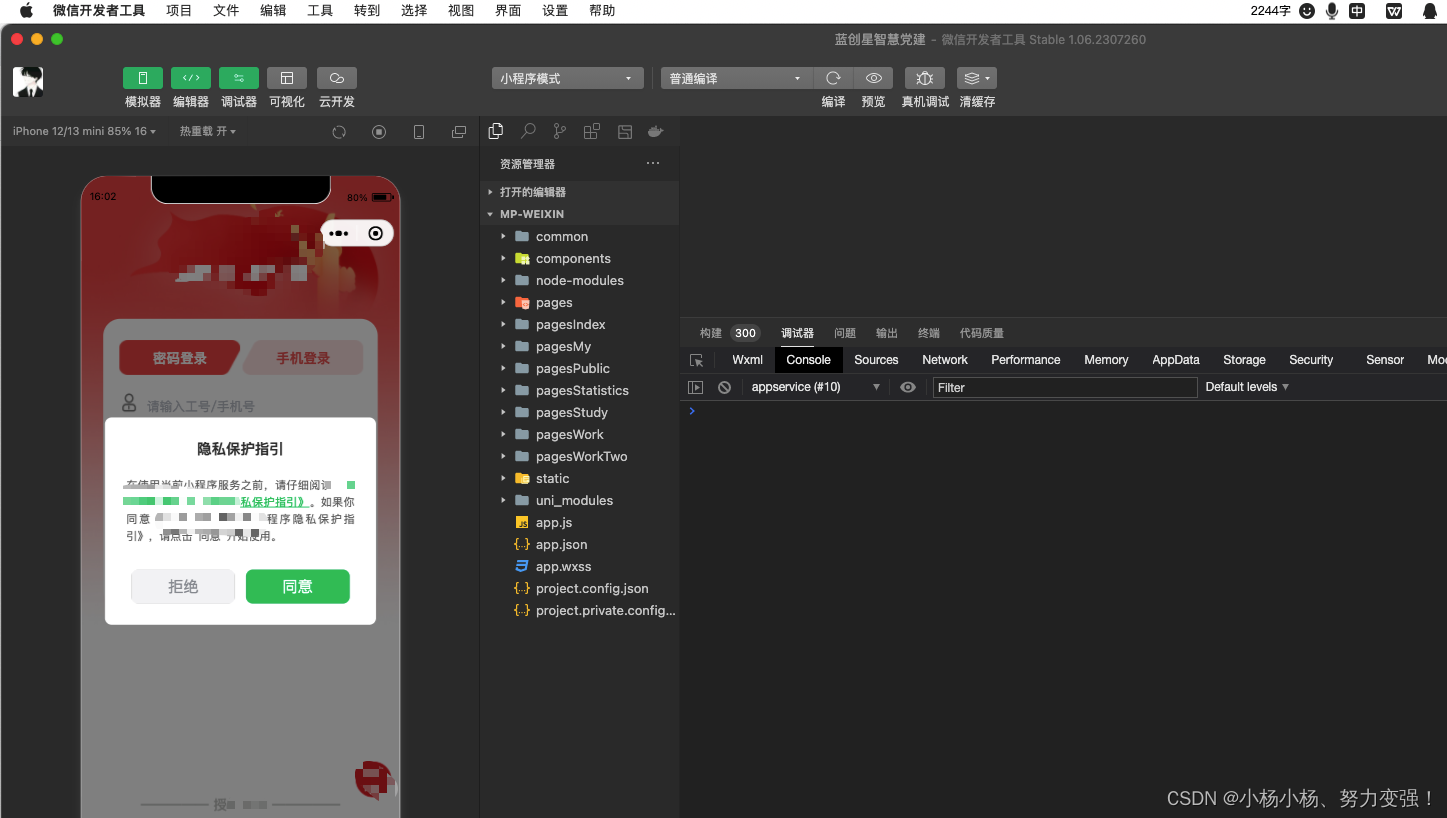
uni-app 新增 微信小程序之新版隐私协议
一、manifest.json中配置 "__usePrivacyCheck__": true 二、编写封装后的组件 <template><view class"privacy" v-if"showPrivacy"><view class"content"><view class"title">隐私保护指引</…...
nbcio-boot移植到若依ruoyi-nbcio平台里一formdesigner部分(四)
到目前为止,虽然基础的formdesigner部分已经完成,但流程用formdesigner提交与审批过程中的显示还有问题。 1、后端部分 其中FormConf修改如下: package com.ruoyi.flowable.core;import lombok.Data;import java.util.List; import java.uti…...

公交查询系统
目录 需求分析 1 概述 2 课题分析 3 实现功能步骤 4 项目背景 概要设计 1 系统流程图. 2 功能模块. 3 各功能模块 4 数据存储 5 类设计 三、详细设计 1公交线路查询系统用户界面 2公交信息存储模快 3公交信息查询模块 4用户信息输入和输出模块 四、调试分析 五、使用说明 六、…...

opencv 轮廓顶点重新排序----四边形
def reorder(myPoints):# print(myPoints.shape)# 创建一个与myPoints具有相同形状和类型的数组myPointsNew np.zeros_like(myPoints)# 数组重塑为一个4行2列的数组myPoints myPoints.reshape((4,2))# 计算myPoints数组中每一行(即每个点)的坐标和add …...

【项目实战】【已开源】USB2.0 HUB 集线器的制作教程(详细步骤以及电路图解释)
写在前面 本文是一篇关于 USB2.0 HUB 集线器的制作教程,包括详细的步骤以及电路图解释。 本文记录了笔者制作 USB2.0 HUB 集线器的心路历程,希望对你有帮助。 本文以笔记形式呈现,通过搜集互联网多方资料写成,非盈利性质…...
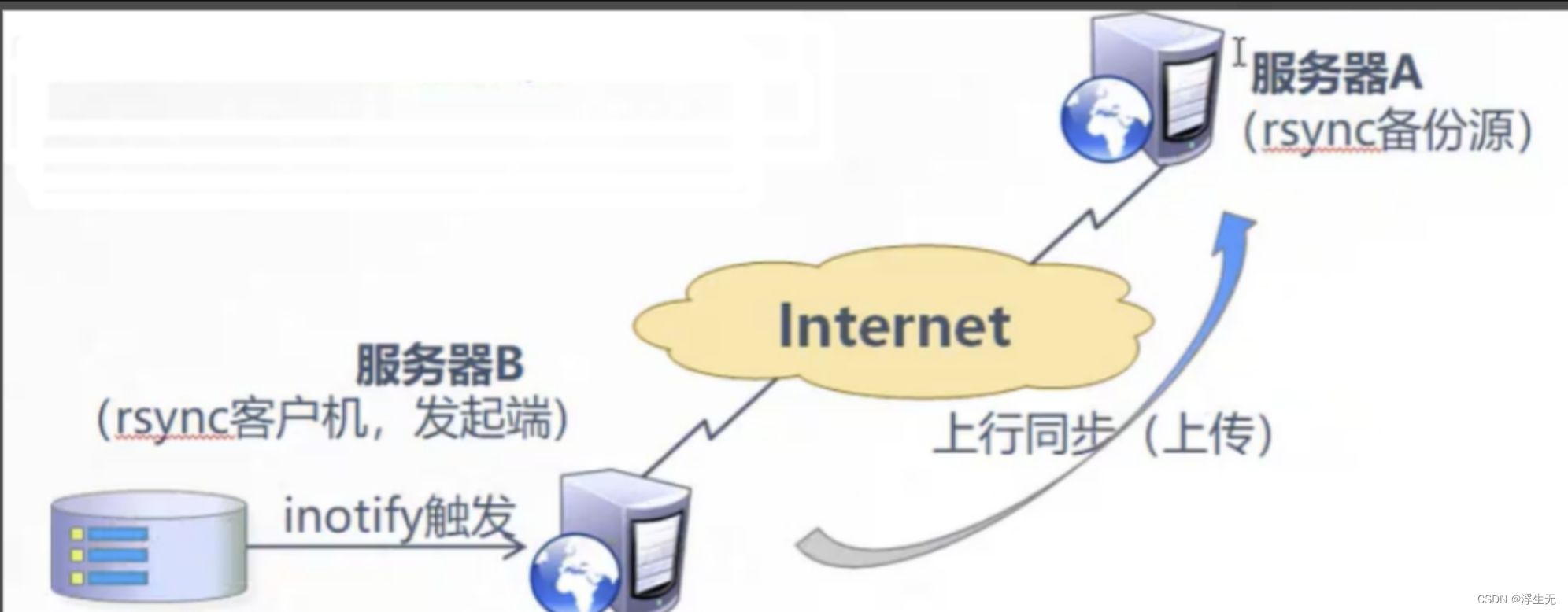
分布式运用之rsync远程同步
一、rsync的相关知识 1.1 rsync简介 rsync(Remote Sync,远程同步)是一个开源的快速备份工具,可以在不同主机之间镜像同步整个目录树,支持增量备份,并保持链接和权限,且采用优化的同步算法&am…...

誉天在线项目~ElementPlus实现浏览页面注意点
浏览按钮 点击浏览按钮,传递列表数据索引值。 根据索引值从列表数据数组中获取当前行数据。 <el-button click"toView(scope.$index)" type"success" size"small"><el-icon><EditPen /></el-icon> 浏览<…...
神经网络-pytorch版本
pytorch神经网络基础 torch简介 torch和numpy import torch import numpy as np np_datanp.arange(6).reshape((2,3)) torch_datatorch.from_numpy(np_data) tensor2arraytorch_data.numpy() print(np_data,"\n",torch_data,"\n",tensor2array)torch的数…...

uniapp vue 页面传参问题encodeURIComponent
页面传参objet json序列化后可能会报错 Uncaught SyntaxError: missing ) after argument list 但不一定是数据有问题,而是json成字符串后,字符串中有特殊字符,所以导致parse的时候格式不对。所以解决方案如下 如果传递参数为对象的时候&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...

NineData数据库DevOps功能全面支持百度智能云向量数据库 VectorDB,助力企业 AI 应用高效落地
NineData 的数据库 DevOps 解决方案已完成对百度智能云向量数据库 VectorDB 的全链路适配,成为国内首批提供 VectorDB 原生操作能力的服务商。此次合作聚焦 AI 开发核心场景,通过标准化 SQL 工作台与细粒度权限管控两大能力,助力企业安全高效…...
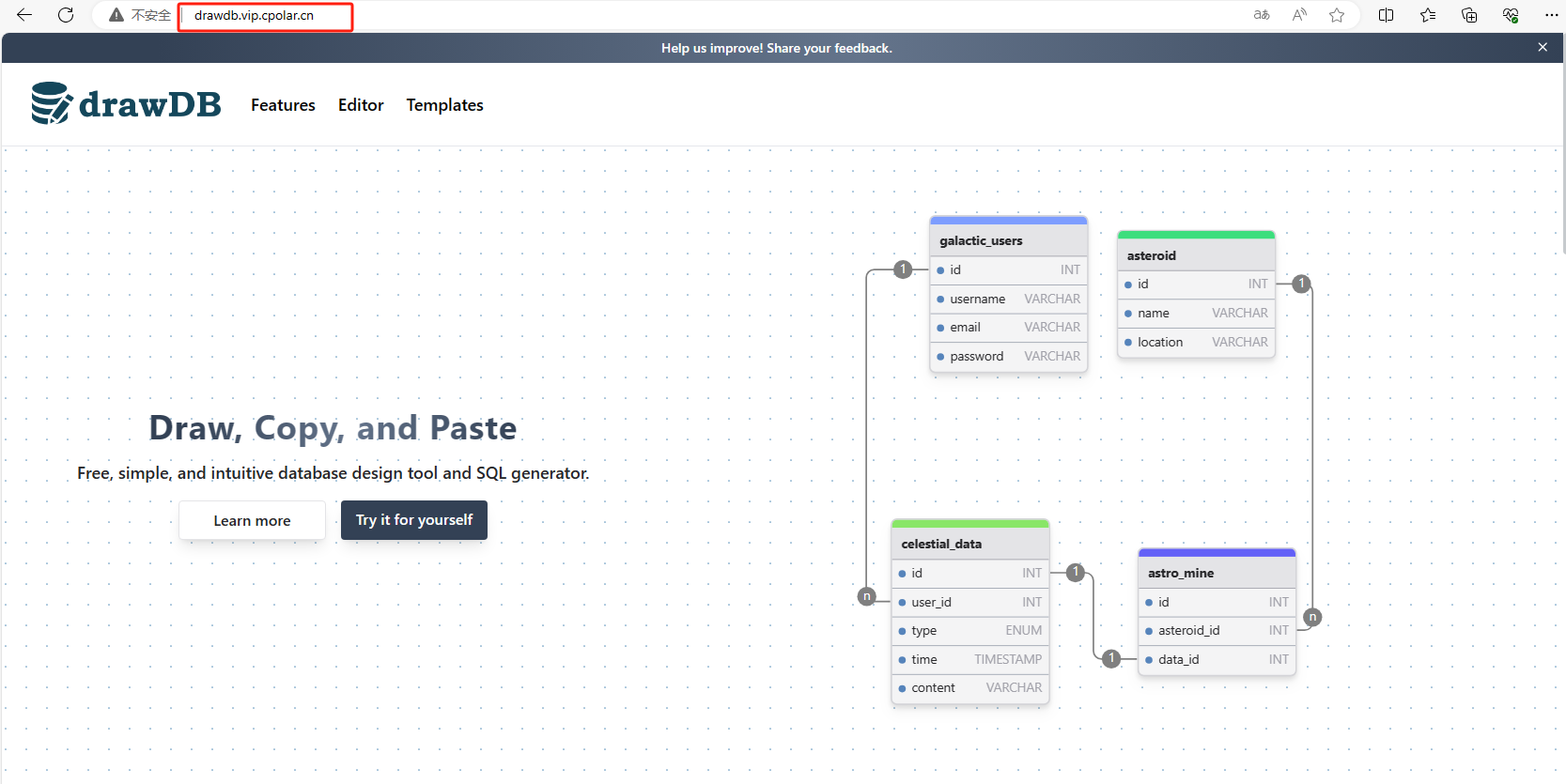
本地部署drawDB结合内网穿透技术实现数据库远程管控方案
文章目录 前言1. Windows本地部署DrawDB2. 安装Cpolar内网穿透3. 实现公网访问DrawDB4. 固定DrawDB公网地址 前言 在数字化浪潮席卷全球的背景下,数据治理能力正日益成为构建现代企业核心竞争力的关键因素。无论是全球500强企业的数据中枢系统,还是初创…...
