当前位置： 首页 > news >正文

Conan安装第三方依赖库时SSL验证失败解决办法

news 2025/7/2 21:35:29

背景

c++跨平台项目使用conan进行三方库依赖管理是比较通用的方案，更换开发环境后突然发现conan无法安装三方库了，报错如下：

zlib/1.2.12: Not found in local cache, looking in remotes...
zlib/1.2.12: Trying with 'conan-center'...
ERROR: Failed requirement 'zlib/1.2.12' from 'conanfile.py (QtConanExample/None)'
ERROR: HTTPSConnectionPool(host='center.conan.io', port=443): Max retries exceeded with url: /v1/ping (Caused by SSLError(SSLError(1, '[SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed (_ssl.c:852)'),))Unable to connect to conan-center=https://center.conan.io
1. Make sure the remote is reachable or,
2. Disable it by using conan remote disable,
Then try again.
CMake Error at build/conan.cmake:651 (message):Conan install failed='1'
Call Stack (most recent call first):CMakeLists.txt:199 (conan_cmake_install)-- Configuring incomplete, errors occurred!

字面意思就是SSL证书验证失败了。

解决办法

删除~/.conan/cacert.pem, 然后重试即可。

相关文章：

Conan安装第三方依赖库时SSL验证失败解决办法

背景 c跨平台项目使用conan进行三方库依赖管理是比较通用的方案，更换开发环境后突然发现conan无法安装三方库了，报错如下： zlib/1.2.12: Not found in local cache, looking in remotes... zlib/1.2.12: Trying with conan-center... ERROR…...

编程日记 2023/9/16 0:09:34

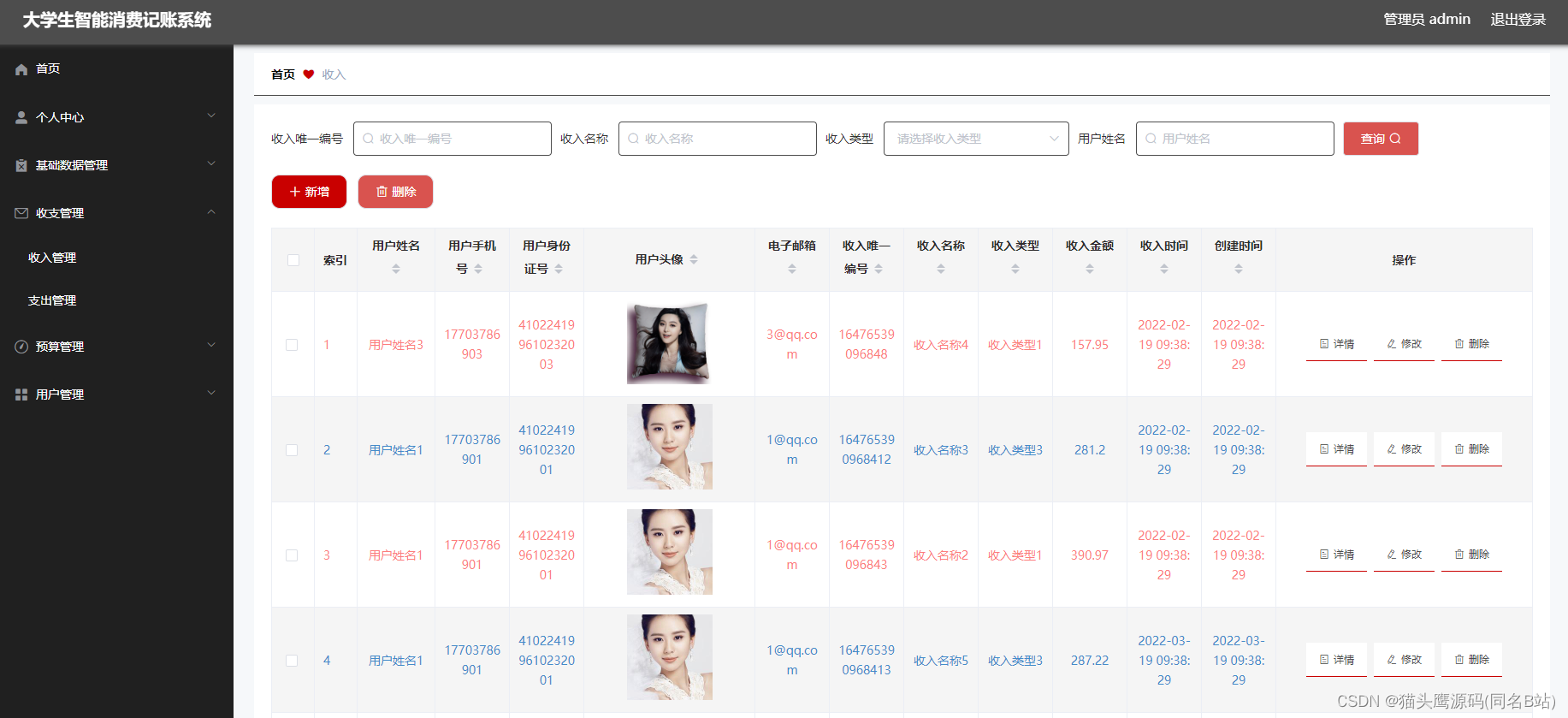
基于springboot+vue的大学生智能消费记账系统

博主主页：猫头鹰源码 博主简介：Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容：毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

编程日记 2023/9/16 0:08:32

Java——》synchronized的使用

推荐链接： 总结——》【Java】 总结——》【Mysql】 总结——》【Redis】 总结——》【Kafka】 总结——》【Spring】 总结——》【SpringBoot】 总结——》【MyBatis、MyBatis-Plus】 总结——》【Linux】 总结——》【MongoD…...

编程日记 2023/9/16 0:07:31

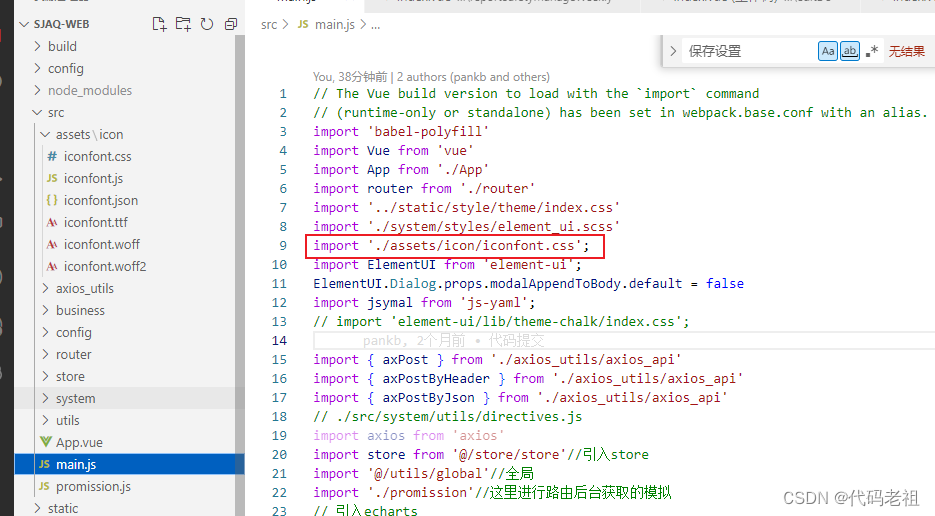
vue+element使用阿里的图标库保存图标

阿里图标网站iconfont-阿里巴巴矢量图标库 我想使用保存图标，但是element的图标库没有找到可用的，首先在阿里的图标网站搜索保存 发现这个还不错 点击添加入库 点击购物车 点击添加至项目 点击下载到本地 把下载的压缩包里面的文件拖到自己项目里面 在m…...

编程日记 2023/9/16 0:05:28

Day 01 web前端基础知识

首先我们要了解什么事前端？ 先简单用文字介绍一下： 一、入门知识 Web前端是指网站或应用程序的用户界面部分。它包括HTML、CSS、JavaScript等语言和技术，用于创建用户可浏览和交互的网页。Web前端的特点在于其交互性和动态性，可…...

编程日记 2023/9/16 0:04:27

Redis 高可用之持久化

目录 Redis 高可用 Redis 持久化 RDB 持久化 触发条件 执行流程 启动时加载 修改配置文件 AOF 持久化 配置 执行流程 命令追加(append) 文件写入(write)和文件同步(sync) 文件重写(rewrite) 文件重写的流程 RDB和AOF的优缺点 Redis 高可用 在web服务器中&…...

编程日记 2023/9/16 0:00:23

生成元 rust解法

如果x加上x的各个数字之和得到y，就说x是y的生成元。给出n（1≤n≤100000），求n的最小生成元。无解输出0。例如，n216，121，2005时的解分别为198，0，1979。 【分析】 本题看起来…...

编程日记 2023/9/15 23:59:22

某ERP系统存在RCE漏洞

文章目录 前言声明一、产品简介二、影响资产三、资产发现四、漏洞测试五、修复方案前言 企望制造纸箱行业ERP系统存在RCE漏洞，攻击者可通过特定Payload注入获取敏感信息。 声明 请勿利用文章内的相关技术从事非法测试，由于传播、利用此文所提供的信息或者工具而造成的任何直…...

编程日记 2023/9/15 23:57:20

ElasticSearch 因为索引字段改变，平滑迁移索引

问题： 某个索引创建时，没有按照想要的mapping,进行创建。 有个字段是text，不是想要的keyWord 此时需要重新按照mapping创建新索引，并迁移数据， 一、不使用别名的方式迁移 1. 创建新索引： 使用 Elastics…...

编程日记 2023/9/15 23:56:20

invalid use of incomplete type ‘class Ui::xxx‘

MainWindow 引用自定义窗口报错：invalid use of incomplete type class Ui::xxx mainwindow.cpp #include "mainwindow.h" #include "ui_mainwindow.h" #include "form.h" form.cpp #include "form.h" #include "…...

编程日记 2023/9/15 23:55:19

变压器寿命预测（python代码，Logistic Regression模型预测效果一般，可以做对比实验）

1.数据来源官网：Data for: Root cause analysis improved with machine learning for failure analysis in power transformers - Mendeley Data 点Download All 10kb即可下载数据 2.下载下来后是这样 每一列的介绍： Hydrogen 氢气； Oxyge…...

编程日记 2023/9/15 23:54:18

微信小程序-增加隐私协议弹窗

真的加了非常之久，非常简单的一个功能，但是因为之前没弄过，加上系统有点bug,软件也有点抽风...... 在微信后台配置-更新用户隐私协议信息增加 "__usePrivacyCheck__" : true, 9月15号之后不加也行，好象今天刚刚好9月15…...

编程日记 2023/9/15 23:53:17

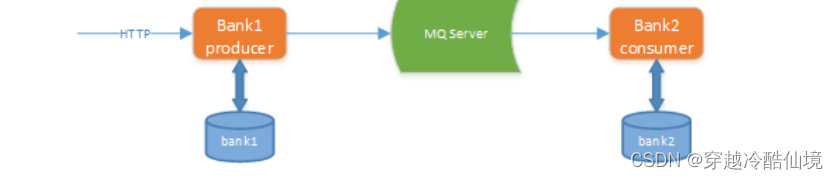
分布式事务解决方案之可靠消息最终一致性

分布式事务解决方案之可靠消息最终一致性 什么是可靠消息最终一致性事务 可靠消息最终一致性方案是指当事务发起方执行完成本地事务后并发出一条消息，事务参与方(消息消费者)一定能 够接收消息并处理事务成功，此方案强调的是只要消息发给事务参与方最终…...

编程日记 2023/9/15 23:52:16

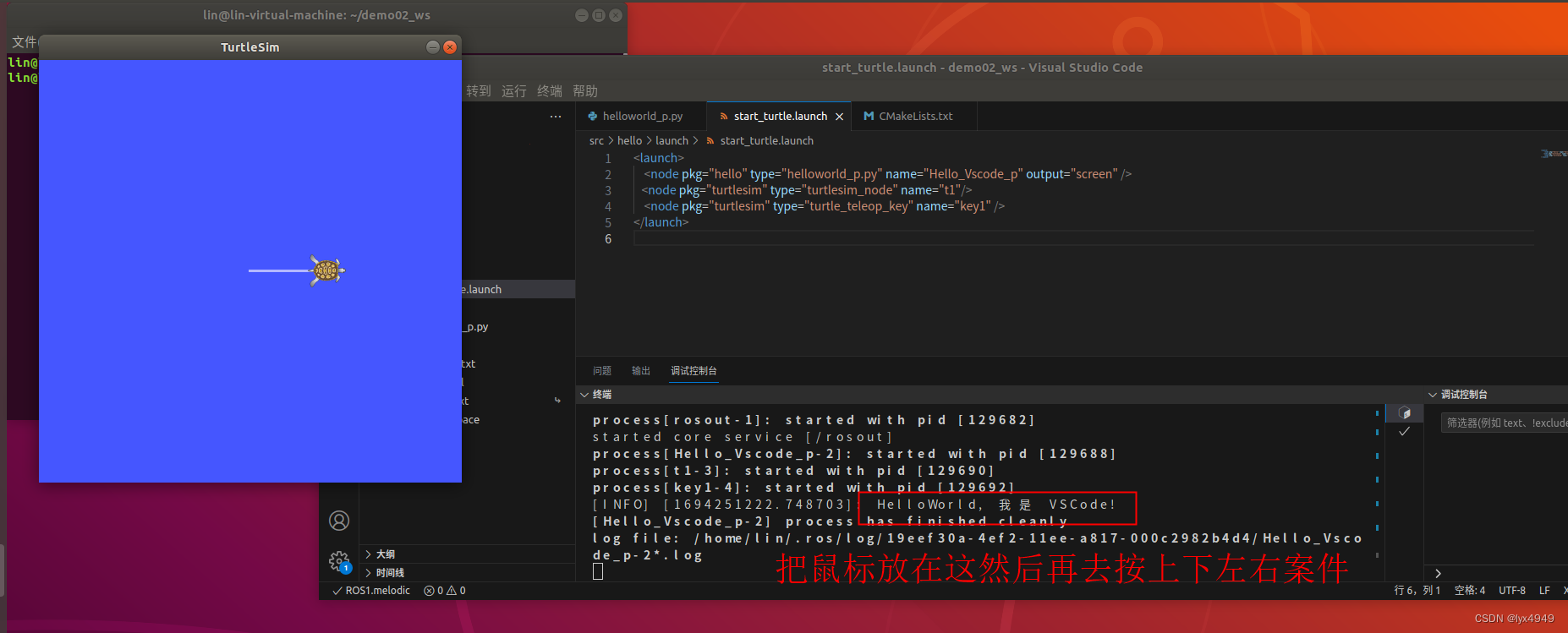
ROS学习笔记(四)---使用 VScode 启动launch文件运行多个节点

ROS学习笔记文章目录 01. ROS学习笔记(一)—Linux安装VScode 02. ROS学习笔记(二)—使用 VScode 开发 ROS 的Python程序（简例） 03. ROS学习笔记(三)—好用的终端Terminator 一、什么是launch文件 虽然说Terminator终端是能够比较方便直观的看运行的节点…...

编程日记 2023/9/15 23:51:15

编译Redis时报错： jemalloc/jemalloc.h: No such file or directory

1.编译Redis时出现错误 运行&#xff1a; [rootcentos01 redis-6.2.7]# make & make install报错&#xff1a; zmalloc.h:50:31: fatal error: jemalloc/jemalloc.h: No such file or directory #include <jemalloc/jemalloc.h> 2.解决步骤 2.1 检查gcc是否安装 [r…...

编程日记 2023/9/15 23:50:13

LLM 05-大模型法律

LLM 05-大模型法律 5.1 简介 在这个教程中&#xff0c;我们将探讨法律对大型语言模型的开发和部署有何规定。我们将会按照以下的步骤进行讨论&#xff1a; 新技术与现有法律的关系 与我们之前的讲座一样&#xff0c;比如关于社会偏见的讲座&#xff0c;我们将要讨论的很多内容…...

编程日记 2023/9/15 23:47:10

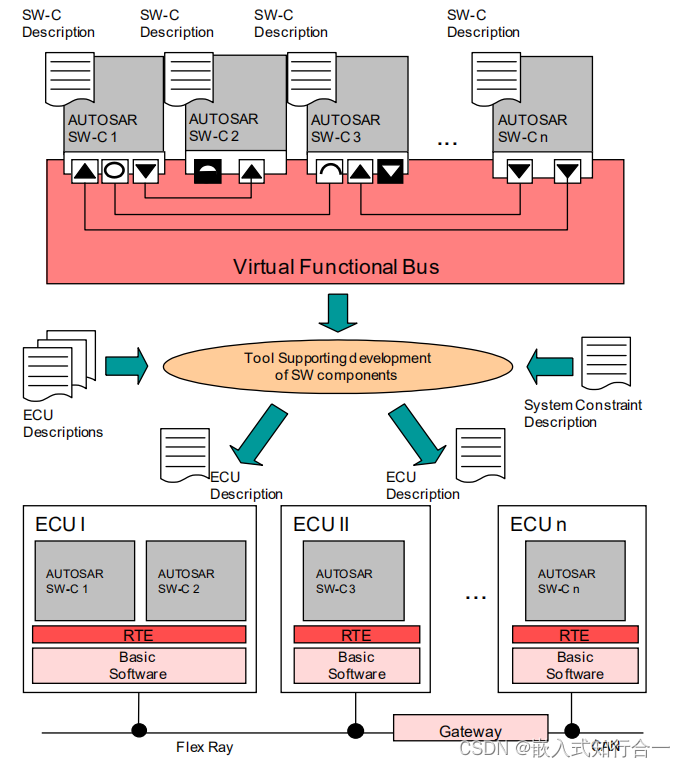
1-5 AUTOSAR数据交换文件ARXML

总目录——AUTOSAR入门详解AUTOSAR入门详解目录汇总&#xff1a;待续中。。。https://xianfan.blog.csdn.net/article/details/132818463 目录 一、Arxml文件 二、各类ARXML文件 一、Arxml文件 arxml文件是AUTOSAR&#xff08;Automotive Open System Architecture&#xff0…...

编程日记 2023/9/15 23:46:10

学习尚硅谷HTML+CSS总结

今天主要学习了颜色像素的四种表达方式&#xff0c;在没学习之前也只会一种RGB颜色的表达方式&#xff0c;虽然其他三种使用的比较少&#xff0c;但有些网页会用其他的表达方式写的我们学过之后就会看得懂&#xff0c;还有文本的设置&#xff0c;字体等等&#xff0c;这些都是后…...

编程日记 2023/9/15 23:45:09

自己设计CPU学习之路——基于《Xilinx FPGA应用开发》

1. 一个32组位宽为32的寄存器堆 框图 代码 regfile.h ifndef __FEGFILE_HEADER__define __REGFILE_HEADER__define HIGH 1b1define LOW 1b0define ENABLE_ 1b0define DISABLE_ 1b1define DATA_W 32define DataBus 31:0define DATA_D 32d…...

编程日记 2023/9/15 23:43:07

数据结构与算法：树

目录 树 定义 结构 二叉树 定义 结构 形式 满二叉树 完全二叉树 存储 链式存储结构 数组 孩子节点 父节点 应用 查找 维持相对顺序 遍历 深度优先遍历 前序遍历 中序遍历 后序遍历 广度优先遍历 层序遍历 二叉堆 定义 自我调整 操作 插入加点 删…...

编程日记 2023/9/15 23:40:03

浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）

✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义&#xff08;Task Definition&…...

编程新知 2025/6/30 3:36:38

SkyWalking 10.2.0 SWCK 配置过程

SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外&#xff0c;K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案&#xff0c;全安装在K8S群集中。 具体可参…...

编程新知 2025/6/15 20:37:19

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能

下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能&#xff0c;包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

编程新知 2025/6/21 3:36:25

基于数字孪生的水厂可视化平台建设：架构与实践

分享大纲&#xff1a; 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年&#xff0c;数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段&#xff0c;基于数字孪生的水厂可视化平台的…...

编程新知 2025/6/16 21:39:46

项目部署到Linux上时遇到的错误（Redis，MySQL，无法正确连接，地址占用问题）

Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败&#xff0c;具体原因是客户端发送了密码认证请求&#xff0c;但Redis服务器未设置密码 1.为Redis设置密码&#xff08;匹配客户端配置&#xff09; 步骤&#xff1a; 1&#xff09;.修…...

编程新知 2025/6/26 10:08:29

GO协程(Goroutine)问题总结

在使用Go语言来编写代码时&#xff0c;遇到的一些问题总结一下 [参考文档]&#xff1a;https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现&#xff1a; 今天在看到这个教程的时候&#xff0c;在自己的电…...

编程新知 2025/6/26 1:16:57

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能

1. 开发环境准备 ​​安装DevEco Studio 3.1​​&#xff1a; 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK ​​项目配置​​&#xff1a; // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

编程新知 2025/6/21 6:36:08

android13 app的触摸问题定位分析流程

一、知识点 一般来说，触摸问题都是app层面出问题，我们可以在ViewRootImpl.java添加log的方式定位；如果是touchableRegion的计算问题，就会相对比较麻烦了，需要通过adb shell dumpsys input > input.log指令，且通过打印堆栈的方式，逐步定位问题，并找到修改方案。 问题…...

编程新知 2025/7/2 8:50:20

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

编程新知 2025/7/1 18:57:58

Python 训练营打卡 Day 47

注意力热力图可视化 在day 46代码的基础上&#xff0c;对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

编程新知 2025/6/22 16:30:09