蓝桥杯打卡Day9
文章目录
- 直角三角形
- 最长平衡串
一、直角三角形IO链接
本题思路:本题就是利用欧几里得距离求解即可。
#include <bits/stdc++.h>int main()
{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int T;std::cin>>T;while(T--){int x1,y1,x2,y2,x3,y3;std::cin>>x1>>y1>>x2>>y2>>x3>>y3;int a=std::pow(std::abs(x2-x1),2)+std::pow(std::abs(y2-y1),2);int b=std::pow(std::abs(x3-x1),2)+std::pow(std::abs(y3-y1),2);int c=std::pow(std::abs(x3-x2),2)+std::pow(std::abs(y3-y2),2);if (a + b == c || a + c == b || b + c == a) printf("Yes\n");else printf("No\n");printf("%.2f\n",std::sqrt(a)+std::sqrt(b)+sqrt(c));}return 0;
}二、最长平衡串IO链接
本题思路:找一个连续的子串, 使得子串中‘0’和‘1’的个数能抵消,利用前缀和a[i]统计前i个字符中有多少个‘1’, 前缀和b[i]统计前i个字符中有多少个‘0’,记该最大连续子串开始地方为 i, 结束地方为 j, 则有a[j]−a[i−1]==b[j]−b[i−1]变形为a[j]−b[j]==a[i−1]−b[i−1],从前往后统计, 记 c 为 a[i]−b[i] 的差值, 用哈希表找到在 i之前的最小a[j]即可。
#include <bits/stdc++.h>constexpr int N=1e6+10;int a[N],b[N];//a[N]用来统计前缀0的和,b[N]用来统计前缀1的和int main()
{std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);std::string s;std::cin>>s;for(int i=1;i<=s.size();i++){a[i]=a[i-1],b[i]=b[i-1];if(s[i-1]=='0') a[i]++;else b[i]++;}int res=0;std::unordered_map<int,int> hash;hash[0]=0;for(int i=1;i<=s.size();i++){int c = a[i] - b[i];//表示当前1和0之前的数量相差多少//用哈希表找到在 i之前的最小a[i]if(hash.count(c)) res = std::max(res, a[i] - a[hash[c]]);else hash[c] = i;//}std::cout<<res*2<<std::endl;return 0;
}相关文章:

蓝桥杯打卡Day9
文章目录 直角三角形最长平衡串 一、直角三角形IO链接 本题思路:本题就是利用欧几里得距离求解即可。 #include <bits/stdc.h>int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int T;std::cin>>T;while(T--){int x…...
C# 辗转相除法求最大公约数
辗转相除法求最大公约数 public static void CalcGCD(int largeNumber, int smallNumber, out int GCD){GCD 1;int remain -1;while (remain ! 0){remain largeNumber % smallNumber;GCD smallNumber;largeNumber smallNumber;smallNumber remain;}}...
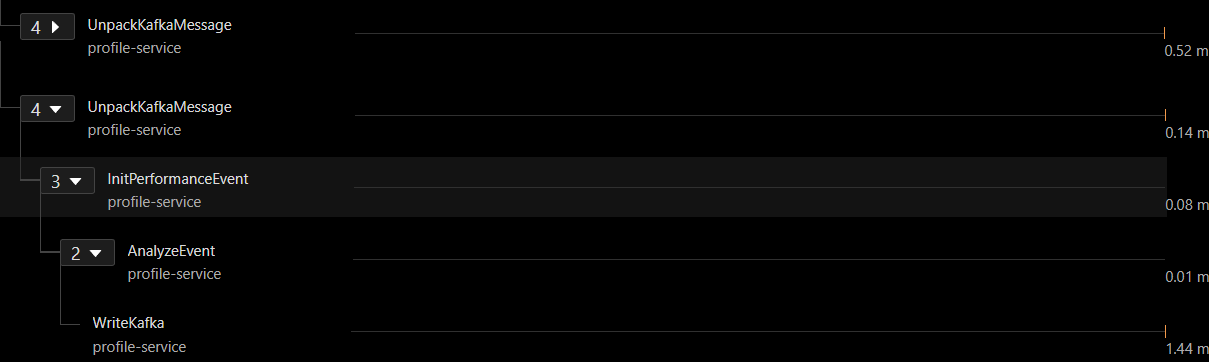
腾讯mini项目-【指标监控服务重构】2023-08-03
今日已办 a,b两组的trace放到一个分支里 可以看到先前的没看到的 profile trace 的耗时,是由于时间跨度较长,没有滑动到 trace 末尾 明日待办 组长会议汇报项目进度和问题...

redis缓存穿透、击穿、雪崩介绍
缓存穿透 概念 缓存穿透指某一特定时间批量请求打进来并访问了缓存和数据库都没有的key,此时会直接穿透缓存直达数据库,从而造成数据库瞬时压力倍增导致响应速度下降甚至崩溃的风险; 解决方案 一、通过布隆过滤器解决 原理:将…...

Redis 基础总结
1、NoSQL概述 1.1 数据库分类 目前数据库分:关系型数据库与非关系型数据库 常用的关系型数据库: Oracle,MySQL,SqlServer,DB2 常用的非关系数据库:Redis,MongoDB,ElasticSearch&…...
)
基于nginx的tomcat负载均衡和集群(超简单)
今天看到"基于apache的tomcat负载均衡和集群配置 "这篇文章成为javaEye热点。 略看了一下,感觉太复杂,要配置的东西太多,因此在这里写出一种更简洁的方法。 要集群tomcat主要是解决SESSION共享的问题,因此我利用memcac…...
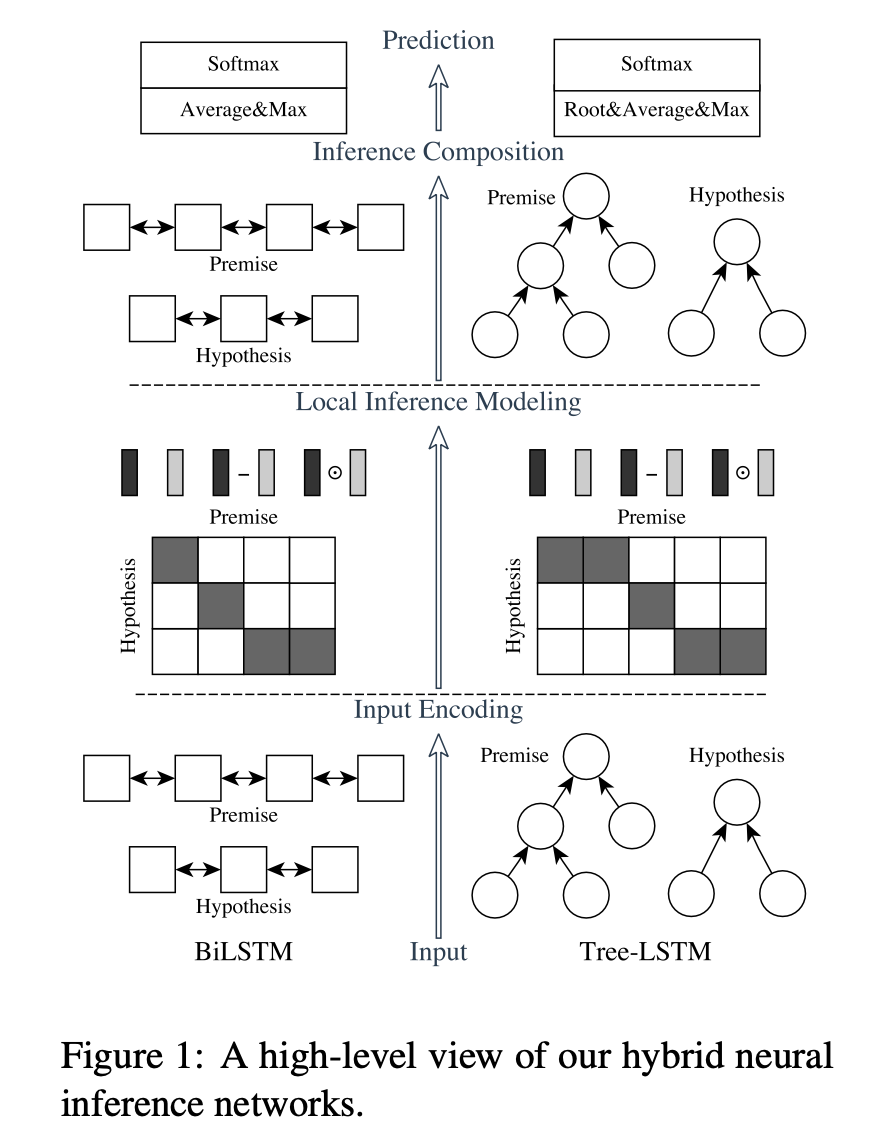
ESIM实战文本匹配
引言 今天我们来实现ESIM文本匹配,这是一个典型的交互型文本匹配方式,也是近期第一个测试集准确率超过80%的模型。 我们来看下是如何实现的。 模型架构 我们主要实现左边的ESIM网络。 从下往上看,分别是 输入编码层(Input Ecoding) 对前…...
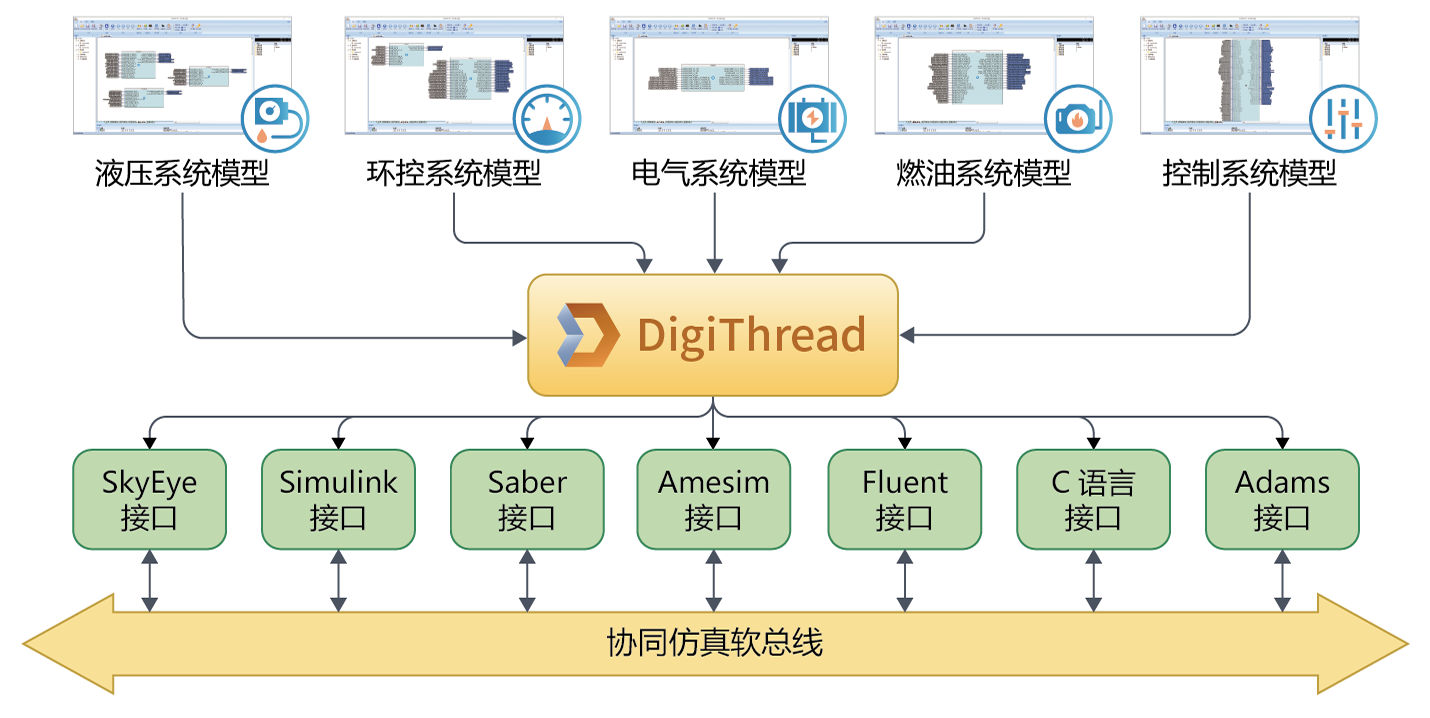
基于虚拟仿真技术的汽车燃油泵控制
在当前激烈的竞争环境下,汽车行业正在加速产业和技术更迭,整车厂对大型ECU嵌入式控制系统和软件的需求迫在眉睫。 然而,复杂而庞大的汽车系统往往由多个物理系统组成,系统所对应的模型都需要在不同的领域实现:发动机、…...

angular:HtmlElement的子节点有Shadow dom时奇怪的现象
描述: 这样写时,会自动跳过shadow dom节点的遍历 const cloneElement this.contentElement.cloneNode(true) as HTMLElement; for(let childNodeIndex 0; childNodeIndex < cloneElement.childNodes.length; childNodeIndex) {element.appendChild…...

栈与队列--删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。 在 S 上反复执行重复项删除操作,直到无法继续删除。 在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。 示例: 输入&#x…...
使用SSH地址拉取远程仓库代码报下面的错误
说明:配置了SSH秘钥后,使用SSH地址克隆代码,依旧无法拉取代码,提示下面这个信息。 Their offer:ssh-rsa,ssh-dss fatal:Could not read from remote repository. Please make sure you have the…...
easycms v5.5 分析 | Bugku S3 AWD排位赛
前言 这个awd打的悲,后台默认用户名密码为admin:admin,但是几乎所有人都改了 而且一进去看到这个cms就有点懵逼,都不知道这个cms是干嘛的(没用过相似的cms) 虽然网上找出了很多相关的漏洞,但是不知道为什…...
成都营运《乡村振兴战略下传统村落文化旅游设计》许少辉八一著作
成都营运《乡村振兴战略下传统村落文化旅游设计》许少辉八一著作...
创邻科技Galaxybase助力SPG推动知识图谱应用落地
1. 知识图谱实践应用:从理论到落地的全景视角 知识图谱,作为一种先进的数据模型和信息表示策略,极大地提升了信息检索与分析的能力。该模型利用图结构,将不同领域、层次和类别的信息有机整合,令复杂的数据关系变得清晰…...

《TCP/IP网络编程》阅读笔记--域名及网络地址
目录 1--域名系统 2--域名与 IP 地址的转换 2-1--利用域名来获取 IP 地址 2-2--利用 IP 地址获取域名 3--代码实例 3-1--gethostbyname() 3-2--gethostbyaddr() 1--域名系统 域名系统(Domain Name System,DNS)是对 IP 地址和域名进行相…...
我的C#基础
using System; namespace HelloWorldApplication }TOC 欢迎使用Markdown编辑器 你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。 为帮助您在CSDN创作的文章获得更多曝光和关注,我们为您提供了专属福利: 已注册且未在CSDN平台发布过…...
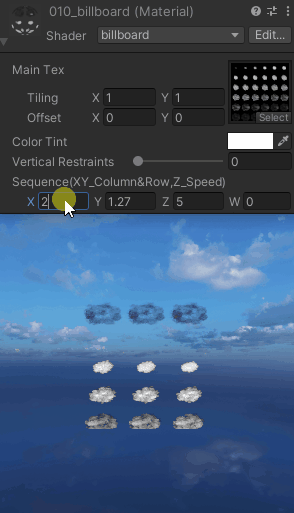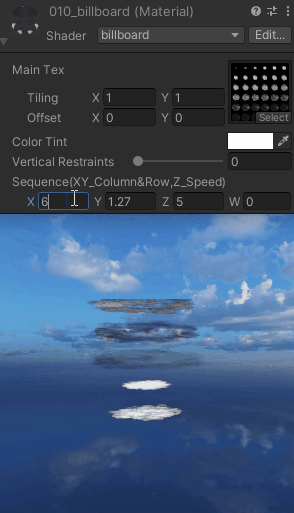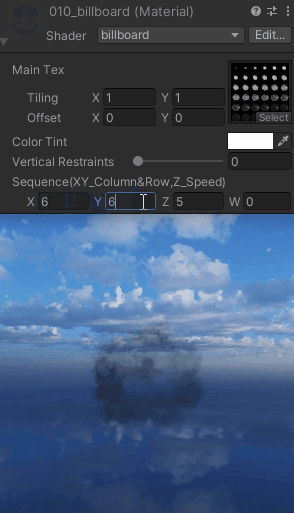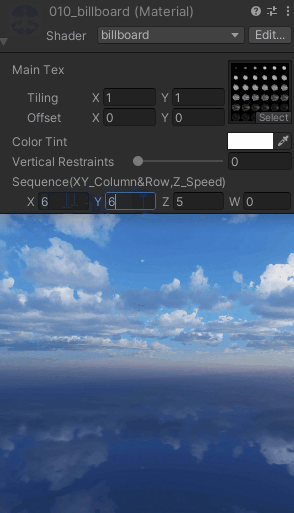
【UnityShaderLab实现“Billboard“始终面向相机_播放序列图的效果_案例分享(内附源码)】
"Billboard"始终面向相机 Shader "billboard" {Properties{_MainTex ("Main Tex", 2D) = "white" {}_Color (...
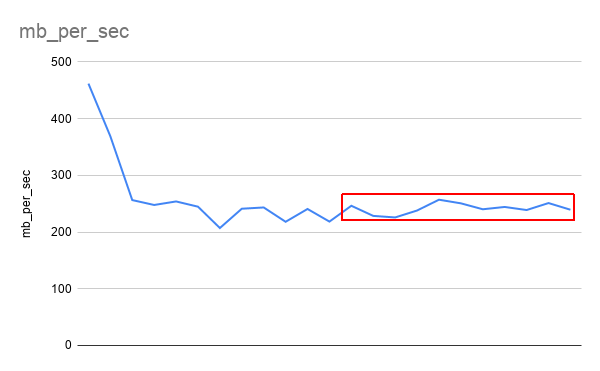
Ceph入门到精通-S3 基准测试工具warp使用入门
S3 基准测试工具。 下载 下载适用于各种平台的二进制版本。 配置 可以使用命令行参数或环境变量配置 Warp。 可以使用 、 在命令行上指定要使用的 S3 服务器,也可以选择指定 TLS 和自定义区域。--host--access-key--secret-key--tls--region 也可以使用 、、 和…...

Docker--未完结
一.Docker是干什么的 在没亲自使用过之前,再多的术语也仅仅是抽象,只有写的人或者使用过的人能看懂。 所以,作为新手来说,只要知道Docker是用于部署项目就够了,下面展示如何用Docker部署项目及Docker常用命令。 二、…...

string的使用和模拟实现
💓博主个人主页:不是笨小孩👀 ⏩专栏分类:数据结构与算法👀 C👀 刷题专栏👀 C语言👀 🚚代码仓库:笨小孩的代码库👀 ⏩社区:不是笨小孩👀 🌹欢迎大…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
