树上背包问题动态规划
目录
树状动态规划概述
示例
求解思路
树状动态规划概述
树状动态规划(Tree DP)是一种在树结构上进行动态规划的方法。在树状DP中,我们利用树的特殊结构性质,通过递归地向下更新子节点的状态,最终得到整个树的最优解或其他需要的信息。
树状DP通常包含以下步骤:
- 定义状态:根据问题的要求,定义每个节点的状态。这可以是一个数值、一个数组、一个结构体等,取决于问题的具体情况。
- 设计转移方程:根据问题的要求,确定每个节点的状态如何从其子节点的状态转移而来。这通常通过遍历节点的子节点,并利用子节点的状态来更新当前节点的状态来实现。
- 确定初始状态:确定叶节点的初始状态,这是递归的终止条件。
- 递归地进行状态转移:从树的顶部开始,递归地向下进行状态转移,直到所有节点的状态都被计算出来。
示例
问题描述: 给定一棵有根树,每个节点有两个属性:权重和价值。节点的权重表示该节点所需要的空间,节点的价值表示该节点的价值。现在有一个给定的背包容量,要求选择一些节点放入背包中,使得总权重不超过背包容量,同时总价值最大。
输入:
- 一棵树的节点数
- 每个节点的权重和价值
- 背包容量
输出:
- 最大的总价值
求解思路
这个例子是一个经典的背包问题在树结构中的应用。我们需要在给定的一棵有根树中,选择一些节点放入背包中,使得总权重不超过背包容量,同时总价值最大。
为了解决这个问题,我们可以使用动态规划的方法。具体思路如下:
-
定义状态:我们定义dp[i][j]表示以节点i为根节点的子树中,在背包容量为j的情况下,可以获得的最大总价值。
-
状态转移方程:对于节点i的每个孩子节点child,我们需要考虑两种情况:
- 不选择child节点:此时dp[i][j]不变。
- 选择child节点:此时需要从剩余容量j减去child节点的权重,即j - tree[child].weight,并从子问题dp[child][j - tree[child].weight]中得到最大价值,再加上child节点的价值tree[child].value。整体来看,选择child节点后的最大总价值为dp[child][j - tree[child].weight] + tree[child].value。
综合考虑上述两种情况,我们可以得到状态转移方程:
dp[i][j] = max(dp[i][j], dp[child][j - tree[child].weight] + tree[child].value)其中,child为节点i的孩子节点。
-
初始化:我们将dp数组初始化为0,表示初始时没有选择任何节点。
-
从根节点开始进行深度优先搜索(DFS),按照上述状态转移方程更新dp数组中的值。最终,dp[1][背包容量]即为所求的最大总价值。
下面是代码中主要部分的解释:
void dfs(int node) {for (int child : tree[node].children) {// 对每个孩子节点进行深度优先搜索dfs(child);// 更新dp数组for (int i = dp[node].size() - 1; i >= tree[node].weight; i--) {dp[node][i] = max(dp[node][i], dp[child][i - tree[node].weight] + tree[child].value);}}
}
在dfs函数中,我们首先对当前节点的每个孩子节点进行深度优先搜索。然后,通过一个循环,从dp[node]的最后一个元素开始向前更新dp[node]的值。这里使用了倒序循环的方式,是因为我们需要保证在更新dp[node][i]时,dp[child][i - tree[node].weight]已经被计算过(即在dp[node]的前面位置)。同时,我们需要确保总权重不超过背包容量,所以我们从tree[node].weight开始遍历。
最后,在主函数中,我们输入节点数和每个节点的权重、价值信息,构建树结构,并调用dfs函数进行求解。最终结果存储在dp[1][背包容量]中。
希望以上详细解释能够帮助你理解这个树状动态规划问题的解决方法。如有任何疑问,请随时提出。
示例:
输入:
节点数 = 5
节点 1: 权重 = 2, 价值 = 3
节点 2: 权重 = 1, 价值 = 2
节点 3: 权重 = 3, 价值 = 4
节点 4: 权重 = 2, 价值 = 2
节点 5: 权重 = 1, 价值 = 1
背包容量 = 5输出:
最大总价值 = 9
C++代码实现:
#include <iostream>
#include <vector>
using namespace std;struct Node {int weight;int value;vector<int> children;
};vector<Node> tree; // 存储树节点的信息
vector<vector<int>> dp; // 存储动态规划的结果void dfs(int node) {for (int child : tree[node].children) {dfs(child);for (int i = dp[node].size() - 1; i >= tree[node].weight; i--) {dp[node][i] = max(dp[node][i], dp[child][i - tree[node].weight] + tree[child].value);}}
}int main() {int n; // 节点数cin >> n;tree.resize(n + 1); // 从编号1开始存储节点信息dp.resize(n + 1, vector<int>(n + 1, 0)); // 初始化动规数组for (int i = 1; i <= n; i++) {cin >> tree[i].weight >> tree[i].value;}// 构建树结构for (int i = 2; i <= n; i++) {int parent;cin >> parent;tree[parent].children.push_back(i);}dfs(1); // 从根节点开始进行深度优先搜索cout << "最大总价值 = " << dp[1][n] << endl;return 0;
}
这段代码首先通过输入构建了一棵树,并使用动态规划方法计算了最大总价值。其中,dfs函数进行了深度优先搜索和动态规划的计算,dp数组用于存储动态规划的结果。
相关文章:

树上背包问题动态规划
目录 树状动态规划概述 示例 求解思路 树状动态规划概述 树状动态规划(Tree DP)是一种在树结构上进行动态规划的方法。在树状DP中,我们利用树的特殊结构性质,通过递归地向下更新子节点的状态,最终得到整个树的最…...

linux查看进程对应的线程(数)
首先,top或ps查看进程列表,确定要查看的进程pid,如下面40698 查看进程的线程情况 查看进程:top -p 40698 查看线程:top -p 40698 -d 3 -H 其中-d是刷新频率 可看到此进程共211个线程,运行中的是211个。…...

Python中的桌面应用开发库有哪些?
Python中有几个受欢迎的桌面应用开发库。以下是其中一些: Tkinter:这是Python的标准GUI库,它提供了构建简单的桌面应用程序的基本组件和功能。 PyQt:这是一个成熟的、功能强大的跨平台图形用户界面框架,它是Python绑定…...
【大数据】Neo4j 图数据库使用详解
目录 一、图数据库介绍 1.1 什么是图数据库 1.2 为什么需要图数据库 1.3 图数据库应用领域 二、图数据库Neo4j简介 2.1 Neo4j特性 2.2 Neo4j优点 三、Neo4j数据模型 3.1 图论基础 3.2 属性图模型 3.3 Neo4j的构建元素 3.3.1 节点 3.3.2 属性 3.3.3 关系 3.3.4 标…...

Windows11系统C盘用户文件夹下用户文件夹为中文,解决方案
说明: 1. 博主电脑为Windows11操作系统,亲测有效,修改后无任何影响,软件都可以正常运行! 2. Windows10系统还不知道可不可行,因为Windows11的计算机管理中没有本地用户和组,博主在csdn上看到很…...
)
Python正则表达式(re)
正则表达式,又称规则表达式,(Regular Expression,在代码中常简写为regex、regexp或RE),是一种文本模式,包括普通字符(例如,a 到 z 之间的字母)和特殊字符(称为…...
【PyTorch 08】如果要手动安装对应的包
例如有时候我们要下载 PyG ,但是需要手动下载,需要进行以下步骤: 网站链接:https://data.pyg.org/whl/ 首先查看当前安装好的Pytorch版本和对应的cuda版本 1. pip list:查看torch版本 2. torch.version.cuda…...
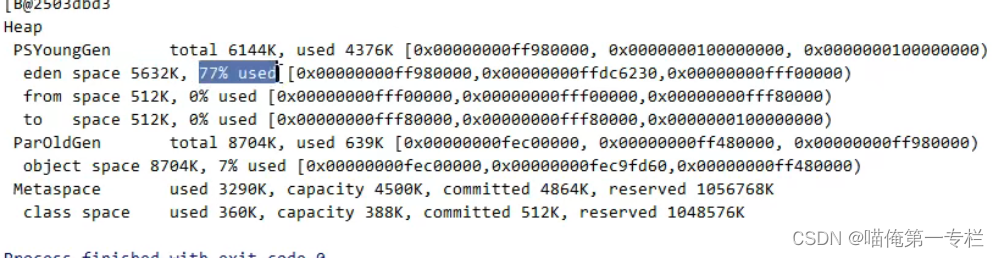
黑马JVM总结(十二)
(1)五种引用_强软弱 实线箭头表示强引用,虚心线表示软弱虚终结器引用 在平时我们用的引用,基本都为强引用 ,比如说创建一个对象通过运算符赋值给了一个变量,那么这个变量呢就强引用了刚刚的对象 强引用的…...
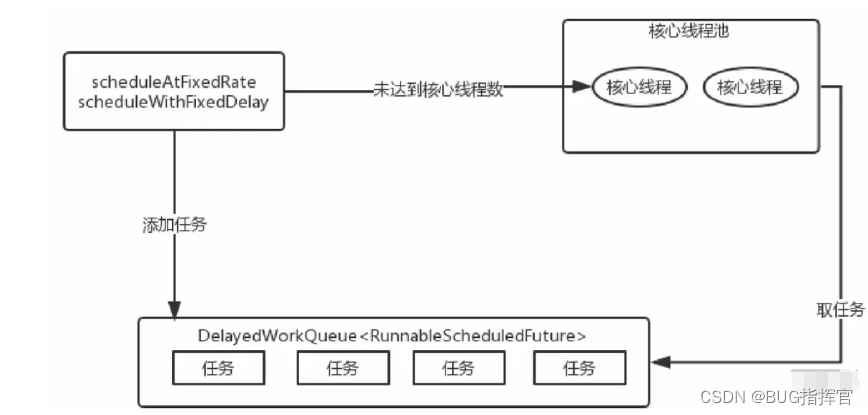
彻底搞懂线程池原理以及创建方式
1. 为什么要使用线程池 在实际使用中,线程是很占用系统资源的,如果对线程管理不善很容易导致系统问题。因此,在大多数并发框架中都会使用线程池来管理线程,使用线程池管理线程主要有如下好处: 降低资源消耗。通过复用…...
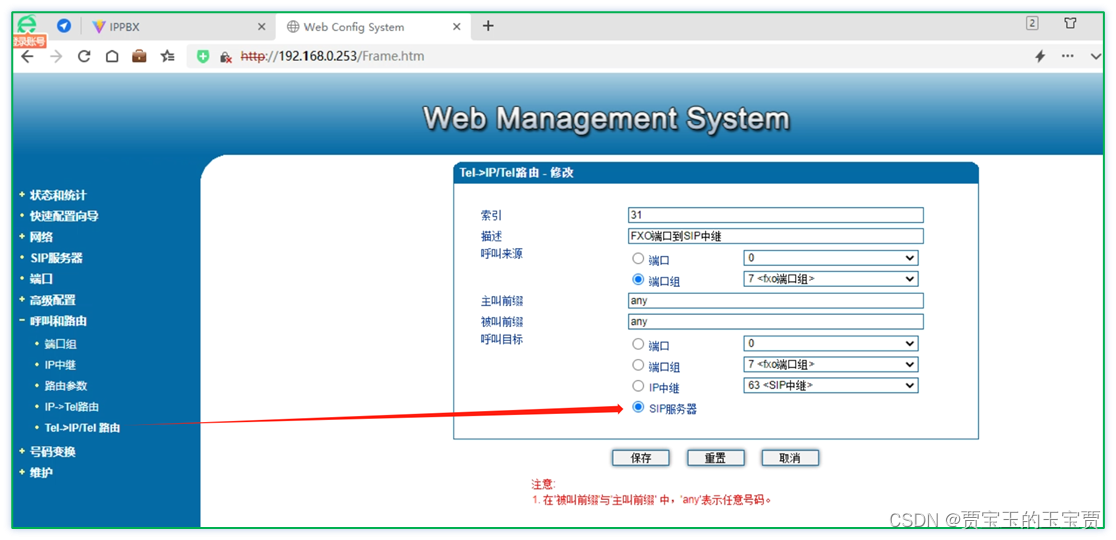
FreeSWITCH 1.10.10 简单图形化界面9 - 鼎兴FXO网关SIP中继内网IPPBX落地
FreeSWITCH 1.10.10 简单图形化界面9 - 鼎兴FXO网关SIP中继内网IPPBX落地 0、 界面预览1、创建一个话务台2、创建PBX SIP中继并设置呼入权限3、设置呼出规则4、设置分机呼出权限5、设置FXO 网关相关信息6、设置FXO网关端口组呼入号码7、设置FXO网关的SIP中继8、设置FXO网关呼叫…...
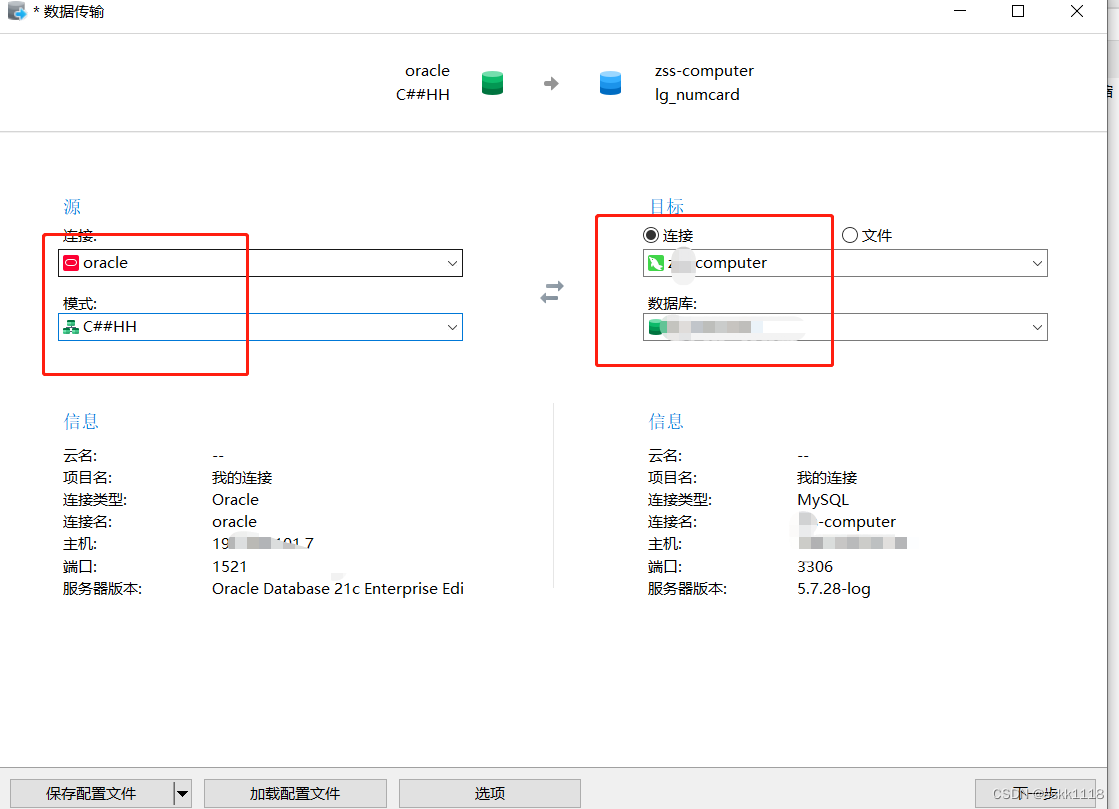
Oracle数据如何迁移导入到MySQL
使用Navicat工具建立数据连接,进行数据传输 1、打开Navicat工具,分别连接Oracle数据库和MySQL数据库。 2、连接源选择你的oracle数据,目标选mysql 即可成功导入...

卡尔曼滤波(Kalman Filter)原理浅析-数学理论推导-1
目录 前言数学理论推导1. 递归算法2. 数学基础结语参考 前言 最近项目需求涉及到目标跟踪部分,准备从 DeepSORT 多目标跟踪算法入手。DeepSORT 中涉及的内容有点多,以前也就对其进行了简单的了解,但是真正去做发现总是存在这样或者那样的困惑…...

Linux 文件创建、查看
touch、cat、more命令 ①touch命令——创建文件 ②cat命令——查看文件内容全部显示 这是txt.txt文件内容 使用cat命令查看 ③more命令——查看文件内容支持翻页 在查看的过程中,通过空格翻页,通过q退出查看...
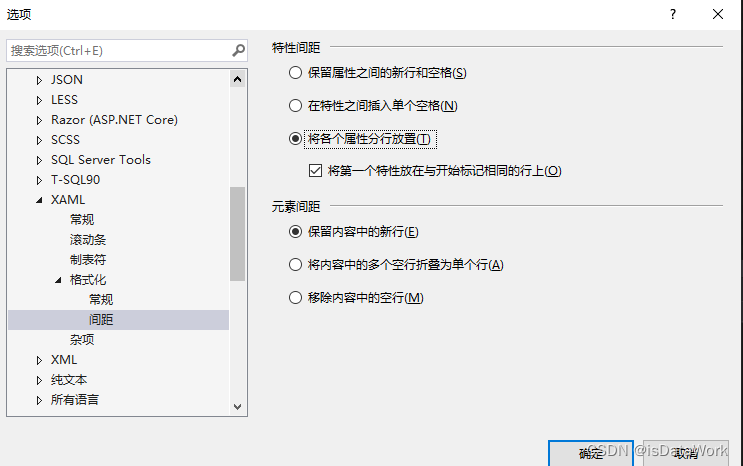
WPF 如何让xmal的属性换行显示 格式化
WPF 如何让UI的xmal 按照下面的格式化显示 首先格式化显示在VS中的快捷键是 Ctrl KD 然后需要配置,工具 选项 -文本编辑器 -xmal -格式化-间距 更改成如下就可以了...

Linux学习之MySQL主从复制
MySQL配置一主一从 环境准备: 两台服务器: Master:192.168.88.53,Slave:192.168.88.54 在两台服务器上安装mysql-server # 配置主服务器192.168.88.53 # 启用binlog日志 [rootmysql53 ~]# yum -y install mysql-ser…...
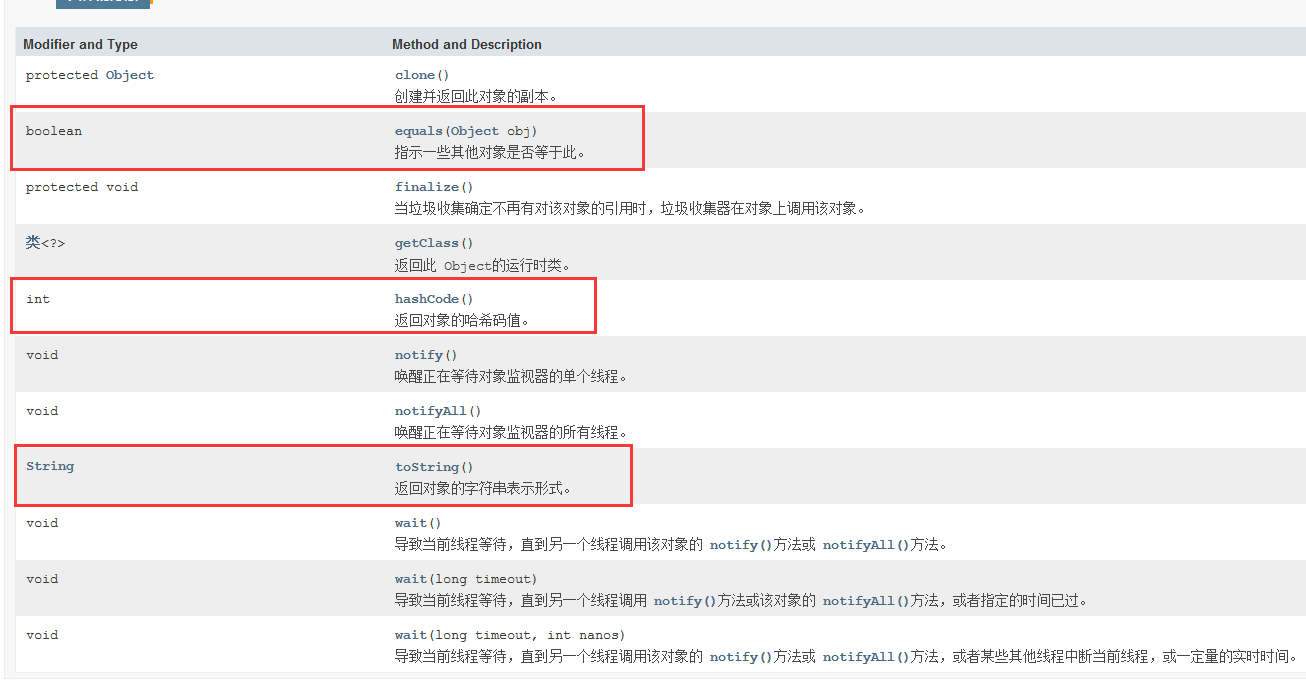
【JavaSE笔记】抽象类与接口
一、抽象类 1、概念 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的,如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。 package demo2…...
详谈操作系统中的内核态和用户态
不知道大家有没有思考过这样一个问题:什么是处理器(CPU)的状态?🤔 其实CPU和人一样,没有执行程序的时候,是没有什么状态的,当它执行的程序是用户程序的时候就叫用户态,当执行的程序是操作系统的代码时就叫系统态或者内…...

OpenWrt KernelPackage分析
一. 前言 KernelPackage是OpenWrt用来编译内核模块的函数,其实KernelPackage后面会调用BuildPackage,这里会一块将BuildPackage也顺便分析,本文以gpio-button-hotplug驱动模块为例,讲解整个编译过程。 gpio-button-hotplug驱动编译…...
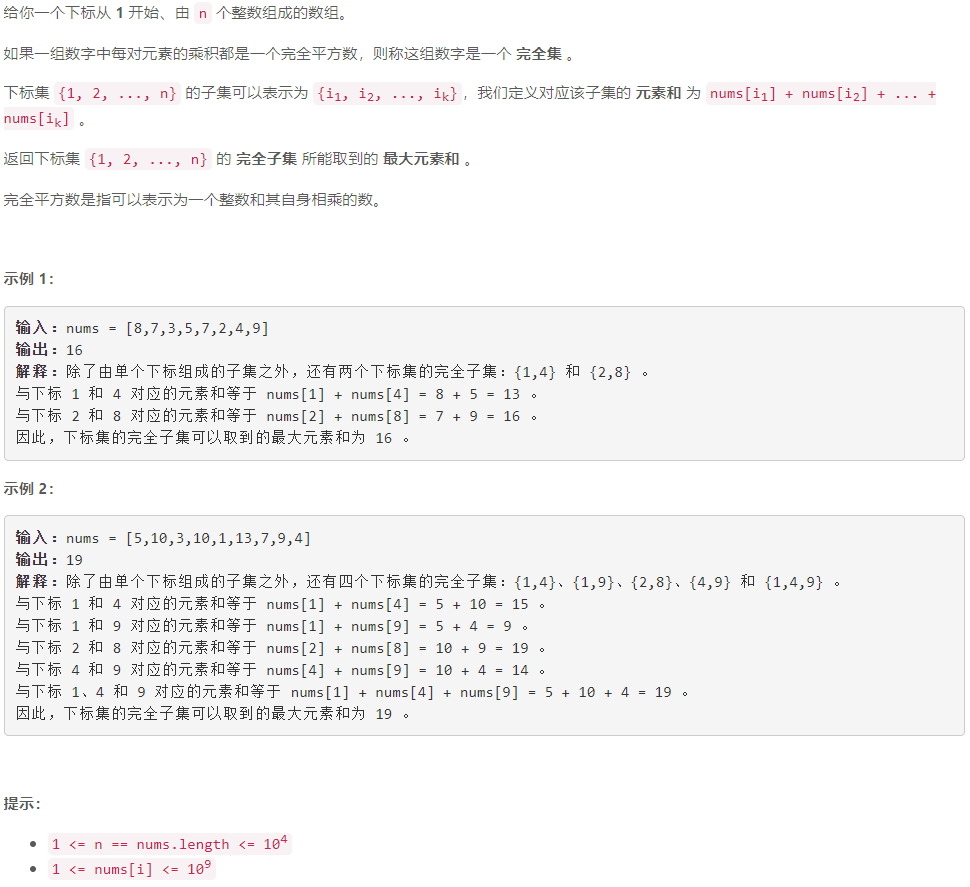
第 363 场 LeetCode 周赛题解
A 计算 K 置位下标对应元素的和 模拟 class Solution { public:int pop_cnt(int x) {//求x的二进制表示中的1的位数int res 0;for (; x; x >> 1)if (x & 1)res;return res;}int sumIndicesWithKSetBits(vector<int> &nums, int k) {int res 0;for (int i…...

ffplay源码解析-main入口函数
main入口函数 初始化 变量、缓存区、SDL窗口初始化等 int main(int argc, char **argv) {int flags;VideoState *is; // av_log_set_level(AV_LOG_TRACE);init_dynload();av_log_set_flags(AV_LOG_SKIP_REPEATED);parse_loglevel(argc, argv, options);/// av_log_set_le…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
