排序——希尔排序
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、希尔排序
- 二、希尔排序动态图
- 三、希尔排序程序代码
- 四、希尔排序习题
- 总结
前言
- 希尔排序定义
- 希尔排序算法分析
- 希尔排序程序代码
- 希尔排序练习题
一、希尔排序
1.定义:先将待排序表分为若干个相同长度的子表(最后一个可不计),分别进行直接插入排序,当基本有序时,再对整体做一次直接插入排序,步骤:
(1)取一个步长d1 ,分为d1组,所有距离为d1倍数的放在一组
(2)各组中进行插入排序
(3)然后取步长d2,重复上述,直到取到步长为1,即所有记录已放在同一组中,再进行直接插入排序
(4)一般的,取d1=n/2 ,di+1=di/2向下取整,并且最后一个为1
二、希尔排序动态图
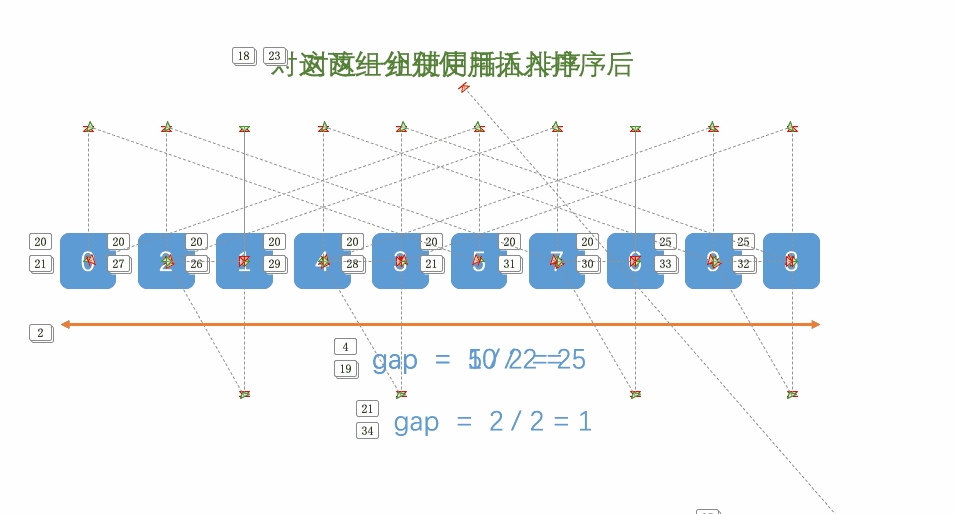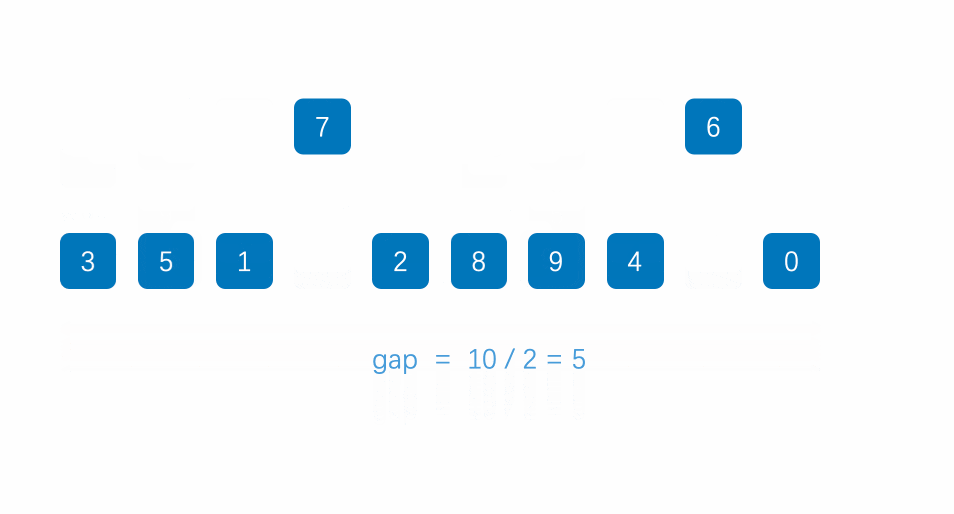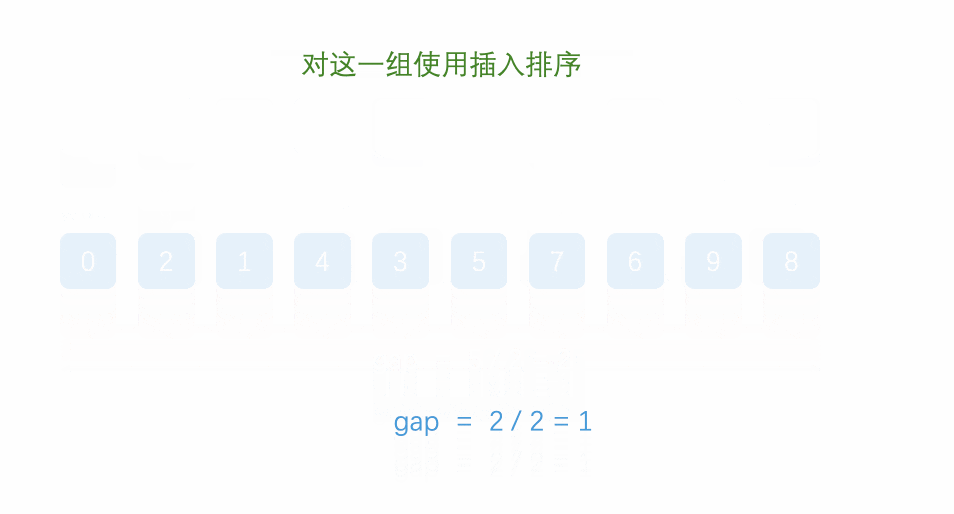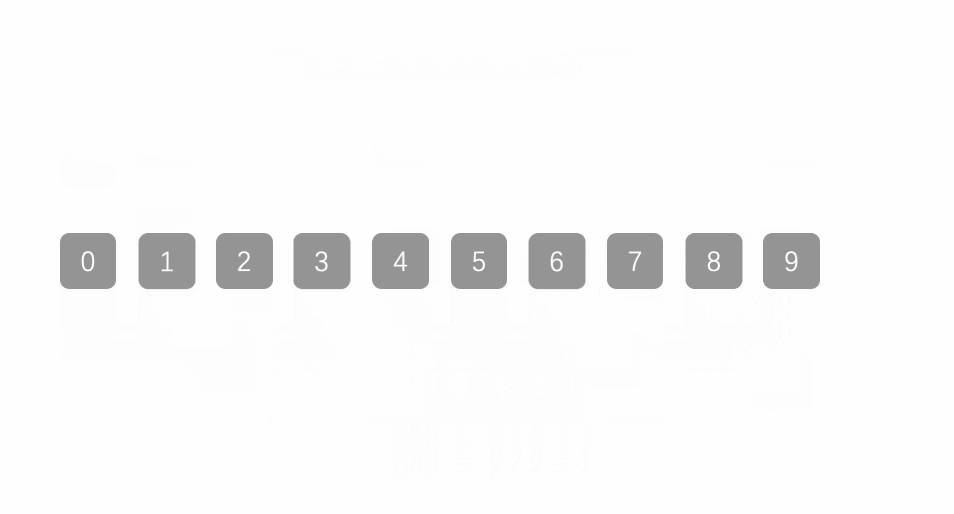
三、希尔排序程序代码
void ShellInsert(elementtype r[n+1],int k){dh=k;while(dh>=1){for(i=dh+1li<=n;i++){r[0]=r[I];j=i-dh;while(j>0&&r[j]>r[0]){r[j+dh]=r[j];j=j-dh;}r[j+dh]=r[0];}dh=dh/2;}
}
2.效率:空间为O(1),时间效率最坏情况下 O(n2)
3.稳定性:相同关键字会被划分为不同子表中,所以为不稳定算法
4.适用性:仅适用于顺序表
四、希尔排序习题
例题:
9、1、2、5、7、4、8、6、3、5
第一趟排序:4、1、2、3、5、9、8、6、5、7
第二趟排序:2、1、4、3、5、6、5、7、8、9
第三趟排序:1、2、3、4、5、5、6、7、8、9
总结
- 希尔排序定义
- 希尔排序算法分析
- 希尔排序程序代码
- 希尔排序练习题
相关文章:

排序——希尔排序
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、希尔排序二、希尔排序动态图三、希尔排序程序代码四、希尔排序习题总结 前言 希尔排序定义希尔排序算法分析希尔排序程序代码希尔排序练习题 一、希尔排序…...
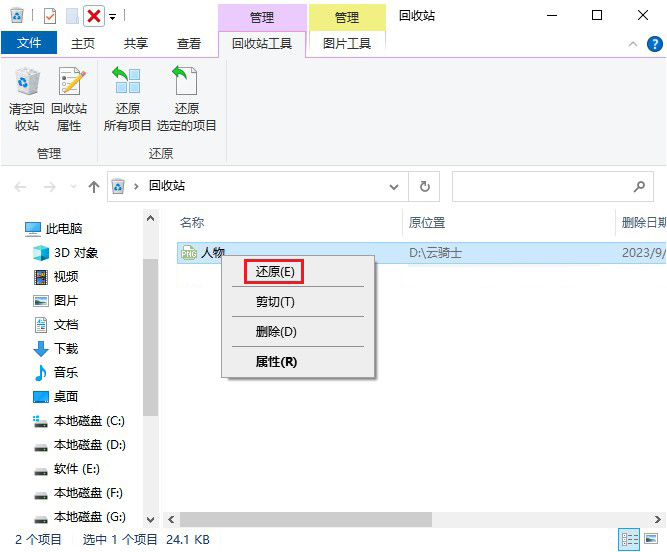
为什么文件夹里的文件看不到?了解原因及应对措施
无论是在个人电脑中还是在其他存储介质上,我们经常会遇到文件夹中的文件突然不可见的情况。这种问题给我们的工作和生活带来了不便,并可能导致数据丢失。本文将分析文件夹中文件看不见的原因,并介绍相应的解决方法,以帮助大家更好…...
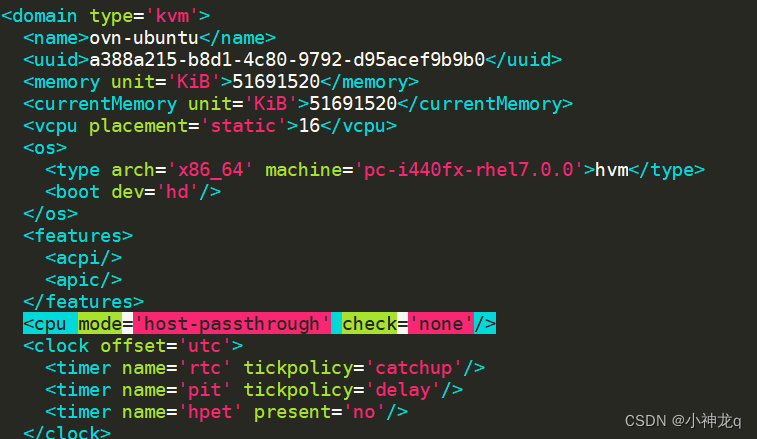
KVM嵌套虚拟化实现
KVM嵌套虚拟化实现 理论 Libvirt主要支持三种 CPU mode host-passthrough: libvirt 令 KVM 把宿主机的 CPU 指令集全部透传给虚拟机。因此虚拟机能够最大限度的使用宿主机 CPU 指令集,故性能是最好的。但是在热迁移时,它要求目的节点的 CPU 和源节点的…...
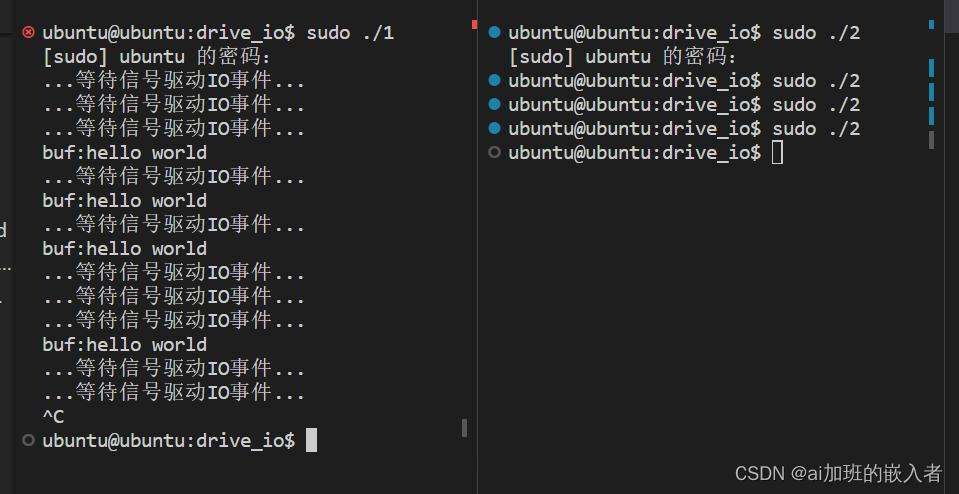
驱动开发,IO模型,信号驱动IO实现过程
1.信号驱动IO框架图 分析: 信号驱动IO是一种异步IO方式。linux预留了一个信号SIGIO用于进行信号驱动IO。进程主程序注册一个SIGIO信号的信号处理函数,当硬件数据准备就绪后会发起一个硬件中断,在中断的处理函数中向当前进程发送一个SIGIO信号…...

左神高级进阶班3(TreeMap顺序表记录线性数据的使用, 滑动窗口的使用,前缀和记录结构, 可能性的舍弃)
目录 【案例1】 【题目描述】 【思路解析】 【代码实现】 【案例2】 【题目描述】 【思路解析】 【代码实现】 【案例3】 【题目描述】 【思路解析】 【代码实现】 【案例4】 【题目描述】 【思路解析】 【代码实现】 【案例1】 【题目描述】 【思路解析】 这里…...

Linux线程
1.进程是资源管理的最小单位,线程是程序执行的最小单位。 2.每个进程有自己的数据段、代码段和堆栈段。线程通常叫做轻型的进程,它包含独立的栈和CPU寄存器状态,线程是进程的一条执行路径,每个线程共享其所附属进程的所有资源,包括…...

C++ 太卷,转 Java?
最近看到知乎、牛客等论坛上关于 C 很多帖子,比如: 2023年大量劝入C 2023年还建议走C方向吗? 看了一圈,基本上都是说 C 这个领域唯一共同点就是都使用 C 语言,其它几乎没有相关性。 的确是这样,比如量化交…...

《Java并发编程实战》第2章-线程安全性
0.概念理解 对象状态:存储在状态变量(例如实例或静态域)中的数据; 线程安全性:当多个线程访问某个类时,这个类始终都能表现出正确的行为,那么就称这个类是线程安全的; 竞态条件&…...

二蛋赠书三期:《C#入门经典(第9版)》
文章目录 前言活动规则参与方式本期赠送书籍介绍作者介绍内容简介读者对象获奖名单 结语 前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,每一位技术…...

Augmented Large Language Models with Parametric Knowledge Guiding
本文是LLM系列文章,针对《Augmented Large Language Models with Parametric Knowledge Guiding》的翻译。 参数知识引导下的增强大型语言模型 摘要1 引言2 相关工作3 LLM的参数化知识引导4 实验5 结论 摘要 大型语言模型(LLM)凭借其令人印…...
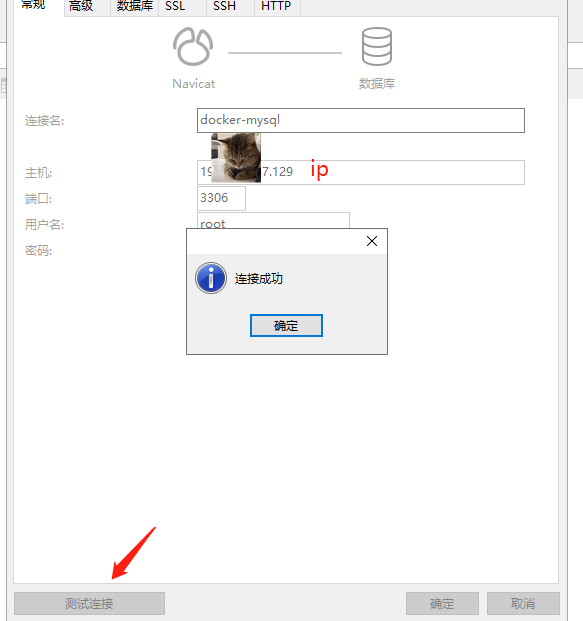
Docker启动Mysql容器并进行目录挂载
一、创建挂载目录 mkdir -p 当前层级下创建 mkdir -p mysql/data mkdir -p mysql/conf 进入到conf目录下创建配置文件touch hym.conf 并把配置文件hmy.conf下增加以下内容使用vim hym.conf即可添加(cv进去就行) Esc :wq 保存 [mysqld] skip-name-resolve character_set_…...
力扣刷题(简单篇):两数之和、两数相加、无重复字符的最长子串
坚持就是胜利 一、两数之和 题目链接:https://leetcode.cn/problems/two-sum/ 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应…...

Spark的基础
实训笔记--Spark的基础 Spark的基础一、Spark的诞生背景二、Spark概念2.1 Spark Core2.2. Spark SQL2.3 Spark Streaming2.4 Spark MLlib2.5 Spark GraphX2.6 Spark R 三、Spark的特点3.1 计算快速3.2 易用性3.3 兼容性3.4 通用性 四、Spark的安装部署4.1 Spark的安装部署就是安…...
如何在idea中新建第一个java小程序
如何在idea中新建第一个java小程序 1.打开软件2.新建项目3.找到安装的jdk文件路径4.继续下一步5.创建项目名称并配置项目路径6.点击完成即可。7.在项目文件的src文件夹下创建java类,程序等7.1其他java项目或文件不能运行的原因: 8.新建类并运行程序9.输入…...

AOP全局异常处理
AOP全局异常处理 由于Controller可能接收到来自业务层、数据层、数据库抛出的异常,因此需要使用AOP思想,进行全局异常处理,异常可通过调试获得。 package org.sinian.reggie.common;import lombok.extern.slf4j.Slf4j; import org.springfram…...
一阶低通滤波器滞后补偿算法
一阶低通滤波器的推导过程和双线性变换算法请查看下面文章链接: PLC算法系列之数字低通滤波器(离散化方法:双线性变换)_双线性离散化_RXXW_Dor的博客-CSDN博客PLC信号处理系列之一阶低通(RC)滤波器算法_RXXW_Dor的博客-CSDN博客_rc滤波电路的优缺点1、先看看RC滤波的优缺点…...

JS中Symbol的介绍
1、 引入Symbol类型的背景 ES5 的对象属性名都是字符串,这容易造成属性名冲突的问题 举例: 使用别人的模块/对象, 又想为之添加新的属性,这就容易使得新属性名与原有属性名冲突 2、Symbol类型简介 symbol是一种原始数据类型 其余原始类型: 未定义(undefined) 、…...

封装统一响应结果类和消息枚举类
在开发中,响应结果都需要统一格式,下面给出一个例子,可自行修改。 package com.lili.utils;import com.fasterxml.jackson.annotation.JsonInclude; import com.lili.enums.AppHttpCodeEnum;import java.io.Serializable;/*** author YLi_Ji…...

应广单片机实现红蓝双色爆闪灯
继续进行点灯,今天来点简单的,红蓝双色爆闪灯,上电即可爆闪,红色接pa.3.pa.4,蓝色接pa6.和pa.7,低电平点亮LED灯,想要高电平点亮,或是驱动N管点亮灯,可以稍作修改。端口电平输出0改1,…...

深入了解OSI模型:计算机网络的七大层次
目录 OSI模型 物理层 数据链路层 网络层 传输层 会话层 表示层 应用层 OSI模型 OSI模型是一个网络通信的概念模型,用于描述计算机网络中各个不同层次之间的通信和功能。它将网络通信分为七个不同的层次,每个层次负责不同的任务,使得网…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
