【面试经典150 | 双指针】判断子序列
文章目录
- 写在前面
- Tag
- 题目来源
- 题目解题
- 解题思路
- 方法一:双指针
- 方法二:动态规划
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【双指针】【动态规划】【字符串】
题目来源
392. 判断子序列

题目解题
判断字符串 s 是不是字符串 t 的子序列,字符串的子序列指的是原字符串删除一些字符或者不删除字符但是不改变原来字符顺序而形成的新的字符串。
解题思路
方法一:双指针
我们使用两个指针 i 和 j,初始化分别指向字符串 s 和 t 的初始位置。从前往后对 s[i] 和 t[j] 进行匹配:
- 如果
s[i] = t[j],则同时向右移动双指针; - 如果
s[i] != t[j],则只移动指向字符串字符的指针j; - 无论是否匹配,都需要移动
j指针; - 最终,如果
i移动到了字符串s的末尾,说明s是t的子序列。
实现代码
class Solution {
public:bool isSubsequence(string s, string t) {int i = 0, j = 0;int n = s.size(), m = t.size();while(i < n && j < m) {if(s[i] == t[j])++i;++j;}return i == n;}
};
复杂度分析
时间复杂度: O ( n + m ) O(n+m) O(n+m), n n n 为 s 的长度, m m m 为 t 的长度。无论匹配是否成功,都至少youyige有一个指针向右移动,两指针的移动总距离为 n + m n+m n+m。
空间复杂度: O ( 1 ) O(1) O(1),仅仅使用了两个指针变量。
方法二:动态规划
方法一有可以进行优化的地方,在方法一中,我们需要枚举匹配 t 中的字符,如果 t 中不匹配的字符很长,我们会有大量的时间浪费在 t 中找下一个匹配的字符。
于是,我们可以先对字符串 t 进行预处理,记录从每个位置开始往后每一个字符第一次出现的位置。
状态
f[i][j] 表示字符串 t 中从位置 i 开始往后字符 j 第一次出现的位置。
状态转移
有如下的状态转移关系:
- 如果
t[i] = j,那么f[i][j] = i; - 否则,
f[i][j] = f[i+1][j]。
根据以上转移关系,我们需要对字符串 t 从后往前进行动态规划。
base case
我们的边界状态为 f[m-1][...],我们置 f[m][...] = m,让 f[m-1][...] 正常转移,如果 f[i][j] = m,则表示从位置 i 开始往后不存在字符 j。
我们通过 f 数组,可以快速定位到字符串 t 后面每一个第一次出现的字符(s 中的字符):
- 如果
f[i][j] = m,则表示从字符串t位置i开始往后不存在s中的字符j,则直接返回false; - 否则,更新
i,从新的位置开始定位s中的字符; - 如果一直没遇到
m,最后返回true。
方法二使用动态规划的方法对字符串 t 进行一次处理,可以大大提高匹配,也是 进阶 题目的一种解法。
实现代码
class Solution {
public:bool isSubsequence(string s, string t) {int n = s.size(), m = t.size();vector<vector<int>> f(m+1, vector<int>(26, 0));for (int i = 0; i < 26; ++i) {f[m][i] = m;}for (int i = m-1; i >= 0; --i) {for (int j = 0; j < 26; ++j) {if (t[i] == j + 'a') {f[i][j] = i;}else f[i][j] = f[i+1][j];}}int start = 0;for (int i = 0; i < n; ++i) {if (f[start][s[i] - 'a'] == m)return false;start = f[start][s[i] - 'a'] + 1;}return true;}
};
复杂度分析
时间复杂度: O ( m × ∣ ∑ ∣ + n ) O(m \times \left| \sum \right| + n) O(m×∣∑∣+n), n n n 为字符串 s 的长度,m 为字符串 t 的长度, ∣ ∑ ∣ \left| \sum \right| ∣∑∣ 为字符集, ∣ ∑ ∣ = 26 \left| \sum \right| = 26 ∣∑∣=26。
空间复杂度: O ( m × ∣ ∑ ∣ ) O( m \times \left| \sum \right|) O(m×∣∑∣),使用的额外空间为对字符串 t 预处理所占用的空间。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 双指针】判断子序列
文章目录 写在前面Tag题目来源题目解题解题思路方法一:双指针方法二:动态规划 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对…...

自动驾驶信息安全方案
目录 1. 修订历史... 3 2. 概述... 4 2.1 目的... 4 2.2 适用范围... 4 2.3 参考文档... 4 2.4 术语和缩写... 4 3. 安全分析... 5 4. 总体设计... 6 4.1 ACU的安全防护... 7 4.1.1 系统安全引导... 7 4.1.2 密钥安全存储... 8 4.1.3 应…...
)
【云原生】kubernetes中pod(最小的资源管理组件)
目录 前言 一、pod 1.1pause容器使得Pod中的所有容器可以共享两种资源: 1.2 通常把Pod分为两类 1.2.1自主式Pod 1.2.2控制器管理的Pod 1.3 Pod 容器的分类 1.3.1基础容器(infrastructure container) 1.3.2初始化容器(initc…...

[DB]数据库--lowdb
[DB]数据库--lowdb lowdb基本应用获取数据数据变更写入文件 lodash的使用获取数据lodash方法使用数据变更写入文件 lowdb lowdb ,是一个基于文件存储的非关系型数据库 基于loadsh的轻量级数据库 可用于在json中存储数据,大小一般为0~200M的json文件 方便简单的数…...
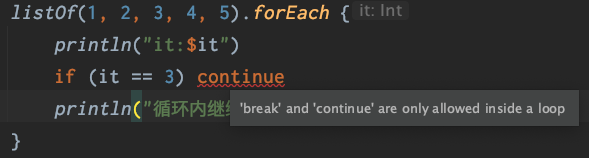
Kotlin | 在for、forEach循环中正确的使用break、continue
文章目录 for循环中使用break、continueLabel标签forEach中如何退出循环资料 Kotlin 有三种结构化跳转表达式: return:默认从最直接包围它的函数或者匿名函数返回。break:终止最直接包围它的循环。continue:继续下一次最直接包围…...

【C++】详解std::mutex
2023年9月11日,周一中午开始 2023年9月11日,周一晚上23:25写完 目录 概述头文件std::mutex类的成员类型方法没有std::mutex会产生什么问题问题一:数据竞争问题二:不一致lock和unlock死锁 概述 std::mutex是C标准库中…...

Matlab图像处理-Lab模型
Lab模型 Lab模型是由CIE(国际照明委员会)制定的一种彩色模型。该模型与设备无关,弥补了RGB模型和CMYK模型必须依赖于设备颜色特性的不足; 另外,自然界中的任何颜色都可以在Lab空间中表现出来,也就是说RGB和…...

分布式ETL工具Sqoop实践
Mysql数据准备 1、在node02节点登录Mysql。 mysql -uroot -proot2、新建数据库testdb。 create database testdb;3、新建数据表ts。 use testdb; create table ts(id int, name varchar(10), age int, sex char(1));4、向表中插入数据。 insert into ts values(10001,张三…...

展会预告 | 图扑邀您共聚 IOTE 国际物联网展·深圳站
参展时间:9 月 20 日- 22 日 图扑展位:9 号馆 9B 35-1 参展地址:深圳国际会展中心(宝安新馆) IOTE 2023 第二十届国际物联网展深圳站,将于 9 月 20 日- 22 日在深圳国际会展中心(宝安…...
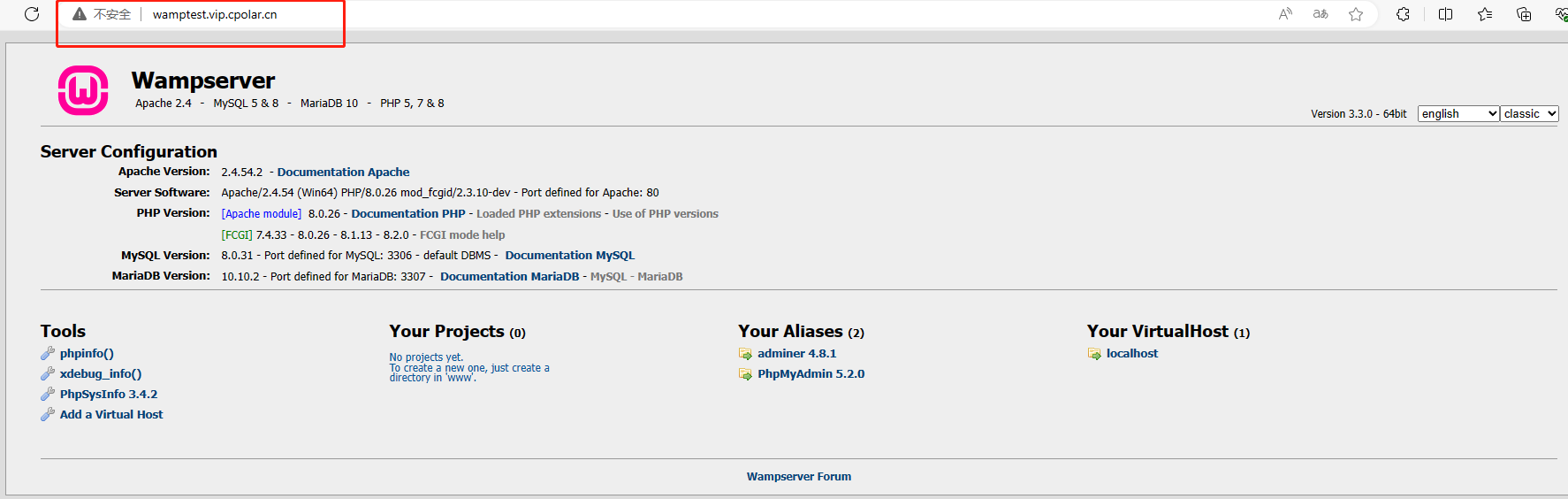
如何下载安装 WampServer 并结合 cpolar 内网穿透,轻松实现对本地服务的公网访问
文章目录 前言1.WampServer下载安装2.WampServer启动3.安装cpolar内网穿透3.1 注册账号3.2 下载cpolar客户端3.3 登录cpolar web ui管理界面3.4 创建公网地址 4.固定公网地址访问 前言 Wamp 是一个 Windows系统下的 Apache PHP Mysql 集成安装环境,是一组常用来…...

iOS添加Mapbox地图库
配置凭据 注册并导航到Account页面。你将需要: 公共访问令牌: 从帐户的tokens页面,你可以复制默认的公共令牌或单击"create a token"按钮来创建新的公共令牌。 带有Downloads:Read范围的秘密访问令牌: 从你帐户的t…...
destoon根据目录下的html文件生成地图索引
因为项目需要,destoon根据目录下的html文件生成地图索引,操作方法,代码如下: <?php $new_array array(); function loopDir($dir,&$new_array,$modurl) {$handle opendir($dir);header("Content-Type:text/xml&qu…...

gRPC之gRPC流
1、gRPC流 从其名称可以理解,流就是持续不断的传输。有一些业务场景请求或者响应的数据量比较大,不适合使用普通的 RPC 调用通过一次请求-响应处理,一方面是考虑数据量大对请求响应时间的影响,另一方面业务场景的设计不一 定需…...

Kafka Shell命令交互
Kafka提供了一个命令行工具,用于管理和与Kafka集群交互。这个命令行工具通常称为Kafka Shell,它允许您执行各种操作,如创建主题、发送和消费消息、查看主题列表等。 以下是一些常用的Kafka Shell命令: 创建主题(Topic): kafka-topics.sh --create --topic my-topic --pa…...

什么是回归测试?
什么是回归测试? 回归测试被定义为一种软件测试类型,以确认最近的程序或代码更改未对现有功能产生不利影响。 回归测试只不过是全部或部分选择已执行的测试用例,然后重新执行以确保现有功能正常运行。 进行此测试是为了确保新代码更改不会…...
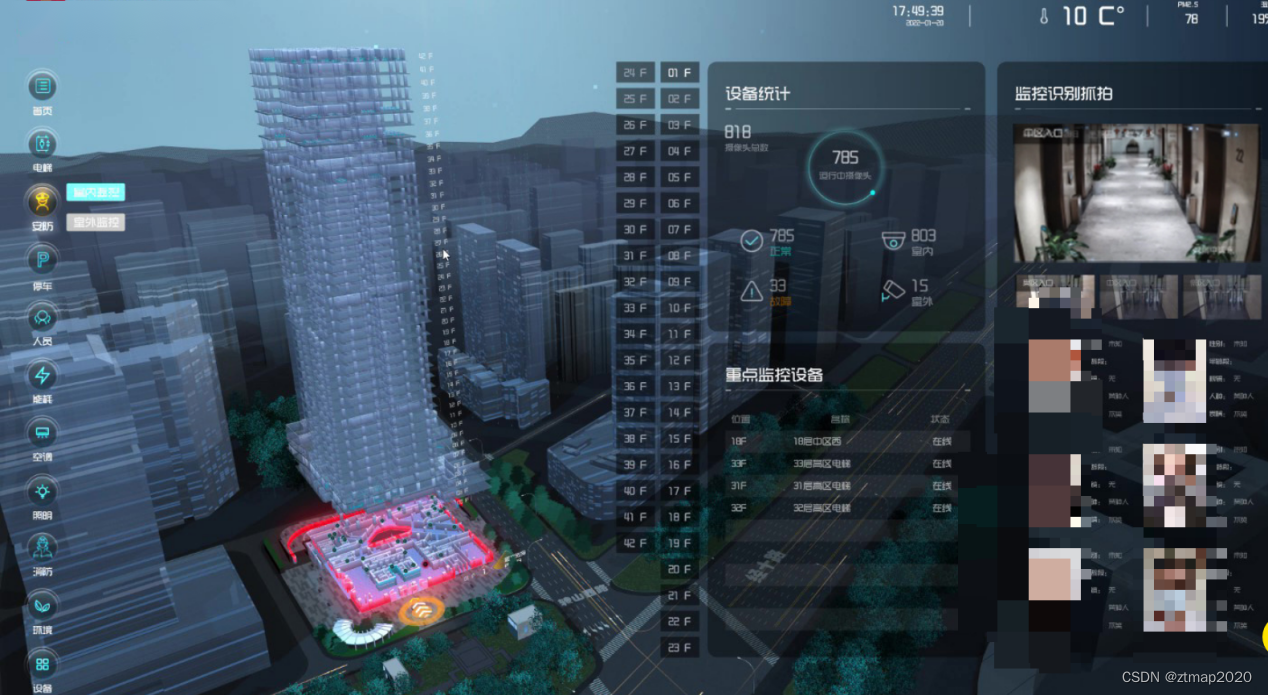
ZTMap是如何在相关政策引导下让建筑更加智慧化的?
近几年随着智慧楼宇概念的深入,尤其是在“十四五规划”“新基建”“数字经济”等相关战略和政策的引导下,智慧楼宇也迎来了快速发展期,对推动智慧城市系统的建设越来越重要。那么究竟什么是智慧楼宇呢?智慧楼宇其实就是整合楼宇内…...

Python:函数和代码复用
嗨喽,大家好呀~这里是爱看美女的茜茜呐 👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~ python源码、视频教程、插件安装教程、资料我都准备好了,直接在文末名片自取就可 1、关于递归函…...
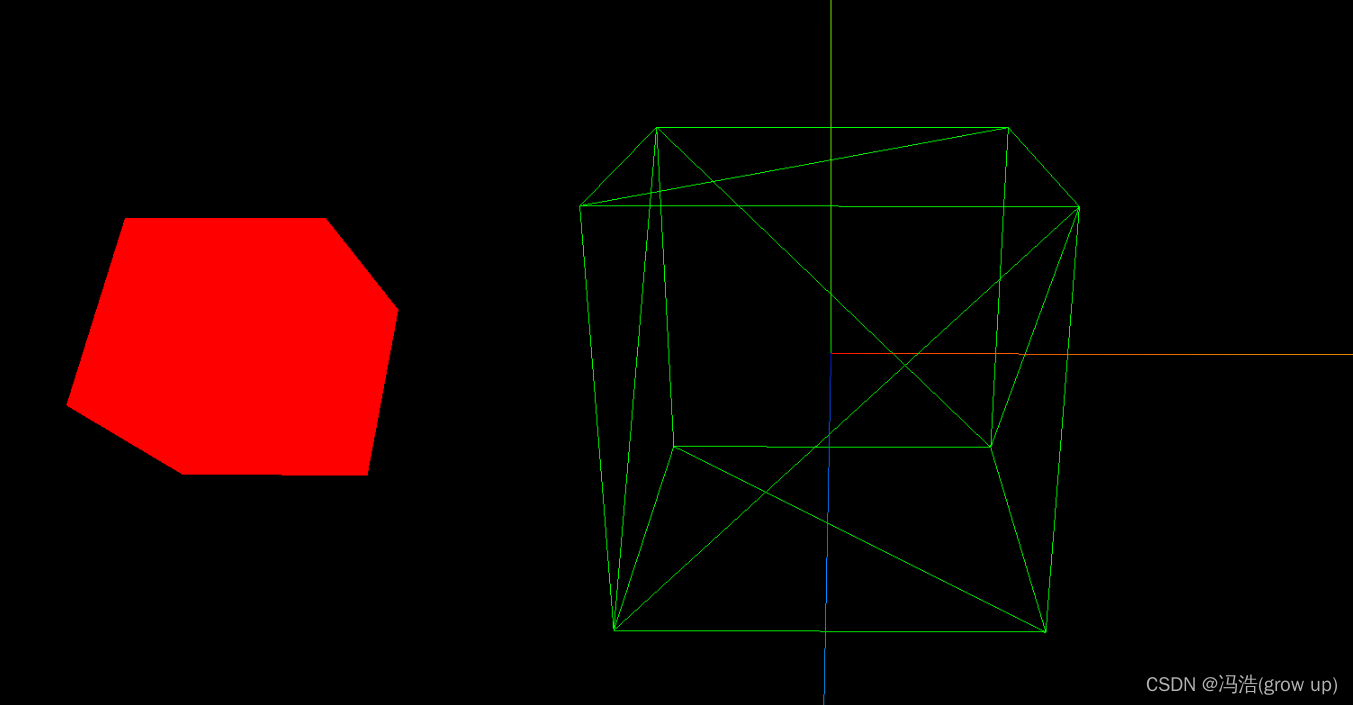
three.js——模型对象的使用材质和方法
模型对象的使用材质和方法 前言效果图1、旋转、缩放、平移,居中的使用1.1 旋转rotation(.rotateX()、.rotateY()、.rotateZ())1.2缩放.scale()1.3平移.translate()1.4居中.center() 2、材质属性.wireframe 前言 BufferGeometry通过.scale()、…...
sql explain
目录 1. sql explain每个字段对应的含义1.1. id1.2. select_type1.3. table1.4. partitions1.5. type1.6. possible_keys1.7. key1.8. key_len1.9. ref1.10. rows1.11. Extra 索引实践联合索引最左列原则全值匹配不建议在索引列上做任何操作, 否则索引会失效转而全表扫描尽量使…...

【LeetCode-简单题】剑指 Offer 05. 替换空格
文章目录 题目方法一:常规做法:方法二:双指针做法 题目 方法一:常规做法: class Solution {public String replaceSpace(String s) {int len s.length() ;StringBuffer str new StringBuffer();for(int i 0 ; i &l…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
