[python 刷题] 238 Product of Array Except Self
[python 刷题] 238 Product of Array Except Self
题目:
Given an integer array
nums, return an arrayanswersuch thatanswer[i]is equal to the product of all the elements ofnumsexceptnums[i].The product of any prefix or suffix of
numsis guaranteed to fit in a 32-bit integer.You must write an algorithm that runs in
O(n)time and without using the division operation.
这里题目中 The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer 就很明显提示说用 prefix sum 了
另外还有就是题目要求的 O ( n ) O(n) O(n) 的时间复杂度,以及不能用除法
题目要求是获取除了自己以外的所有乘积,以题目中的案例 [1,2,3,4],它的乘积可以理解成这样的计算方式:
| 数组 | 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| prefix | 1 | 1 | 1 | 2 | 6 | |
| postfix | 24 | 12 | 4 | 1 | 1 | |
| product | prefix[i] * postfix[i] = 24 | prefix[i] * postfix[i] = 12 | prefix[i] * postfix[i] = 8 | prefix[i] * postfix[i] = 6 |
其中 prefix 是所有的前置乘积,postfix 是所有的后置乘积
解法如下:
class Solution:def productExceptSelf(self, nums: List[int]) -> List[int]:prefix = [1] * (len(nums) + 2)postfix = [1] * (len(nums) + 2)for i in range(2, len(prefix)):prefix[i] = prefix[i - 1] * nums[i - 2]for i in range(len(prefix) - 3, 0, -1):postfix[i] = postfix[i + 1] * nums[i]res = [1] * len(nums)for i in range(0, len(nums)):print(prefix[i + 1])res[i] = prefix[i + 1] * postfix[i + 1]return res但是在实际写的时候发现 map index 的处理稍微麻烦了一些,所以又找了一下其他的写法,发现了一个优化的写法:
class Solution:def productExceptSelf(self, nums: List[int]) -> List[int]:res = [1] * (len(nums))for i in range(1, len(nums)):res[i] = res[i-1] * nums[i-1]postfix = 1for i in range(len(nums) - 1, -1, -1):res[i] *= postfixpostfix *= nums[i]return res这个写法将原本的 3 pass 缩减成了 2 pass,即只有两个循环,主要是因为没有保存 postfix 这个数组,而是一边迭代一边计算 postfix
同时,prefix 的值直接存在了返回值中,跳掉了表格中下标为 0 的占位符
虽然时间和空间的大O还是一样的,不过速度和性能上确实好了不少
相关文章:

[python 刷题] 238 Product of Array Except Self
[python 刷题] 238 Product of Array Except Self 题目: Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i]. The product of any prefix or suffix of nums is guar…...
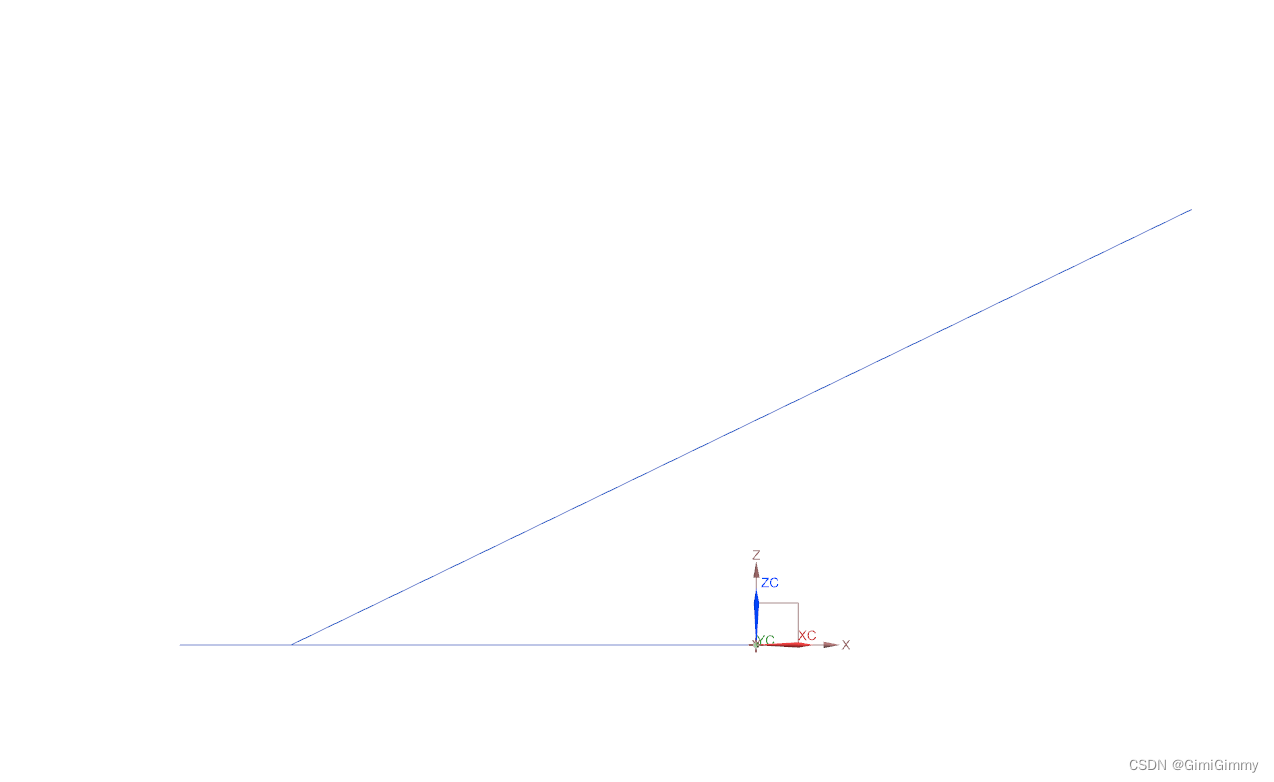
UG NX二次开发(C#)-计算直线到各个坐标系轴向的投影角度
文章目录 1、前言2、需求分析3、NXOpen方法实现3.1 创建基准坐标系3.2 然后计算直线到基准坐标系的轴向角度3.3 代码调用4、测试效果为:1、前言 最近有个粉丝问我如何计算直线到坐标系各个轴向的角度,这里用UG NX二次开发(C#)实现。当然,这里的内容是经验之谈,如果有更好的…...
相互关联)
C# ComboBox 和 枚举类型(Enum)相互关联
C# ComboBox 和 枚举类型(Enum)相互关联 目的 在C# Winform面板上的ComboBox选择项,由程序填写某个Enum的各个枚举项目。 在运行中读取ComboBox的选择项,返回Enum数值。 非编程方法 低阶做法可以在winform设计窗口手动填写,但是不会自动跟…...
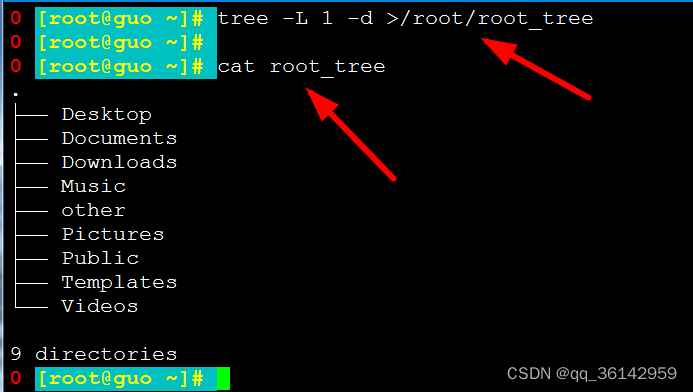
Linux CentOS7 tree命令
tree就是树,是文件或文件名输出到控制台的一种显示形式。 tree命令作用:以树状图列出目录的内容,包括文件、子目录及子目录中的文件和目录等。 我们使用ll命令显示只能显示一个层级的普通文件和目录的名称。而使用tree则可以树的形式将指定…...

软件设计模式系列之九——桥接模式
1 模式的定义 桥接模式是一种结构型设计模式,它用于将抽象部分与其实现部分分离,以便它们可以独立地变化。这种模式涉及一个接口,它充当一个桥,使得具体类可以在不影响客户端代码的情况下改变。桥接模式将继承关系转化为组合关系…...

构造函数的调用规则
#include <iostream> #include <string> using namespace std; class person{ public:int m_age; // person(){ // cout<<"默认构造的调用"<<endl; // } // person(int age){ // m_ageage; // cout<<"有参构造的调用"<…...

第十章:枚举类与注解
10.1:枚举类的使用 当需要定义一组常量时,建议使用枚举类(前提:类的对象只有有限个,确定的) eg: 星期:Mondey、.....、Sunday 性别:Man、.....、Woman 线程状态ÿ…...

ChatGPT:字符串操作问题——提取包含括号的字符串中的题干内容
ChatGPT:字符串操作问题——提取包含括号的字符串中的题干内容 String title p.text().split(“(”)[0];为什么会报错 ChatGPT: 在这段代码中,您正在使用Java处理一个字符串(假设是HTML或文本),尝试将其分…...
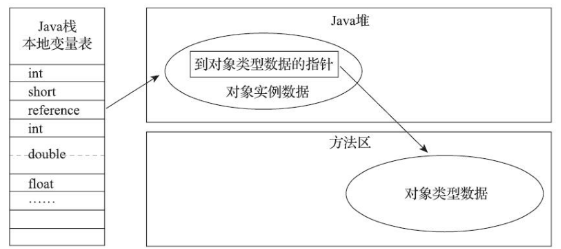
jvm中对象创建、内存布局以及访问定位
对象创建 Java语言层面,创建对象通常(例外:复制、反序列化)仅仅是一个new关键字即可,而在虚拟机中,对象(限于普通Java对象,不包括数组和Class对象等)的创建又是怎样一个过…...

C基础-操作符详解
操作符分类: 算数操作符: - * / % //算数操作符 // int main() // { // // /除法 1.整数除法(除号两端都是整数) 2浮点数除法,除号的两端只要有一个小数就执行小数除法 // // 除法中,除数为0 // int a 7 / 2; /…...

时序预测 | MATLAB实现BO-BiGRU贝叶斯优化双向门控循环单元时间序列预测
时序预测 | MATLAB实现BO-BiGRU贝叶斯优化双向门控循环单元时间序列预测 目录 时序预测 | MATLAB实现BO-BiGRU贝叶斯优化双向门控循环单元时间序列预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 基本介绍 MATLAB实现BO-BiGRU贝叶斯优化双向门控循环单元时间序列预测。…...
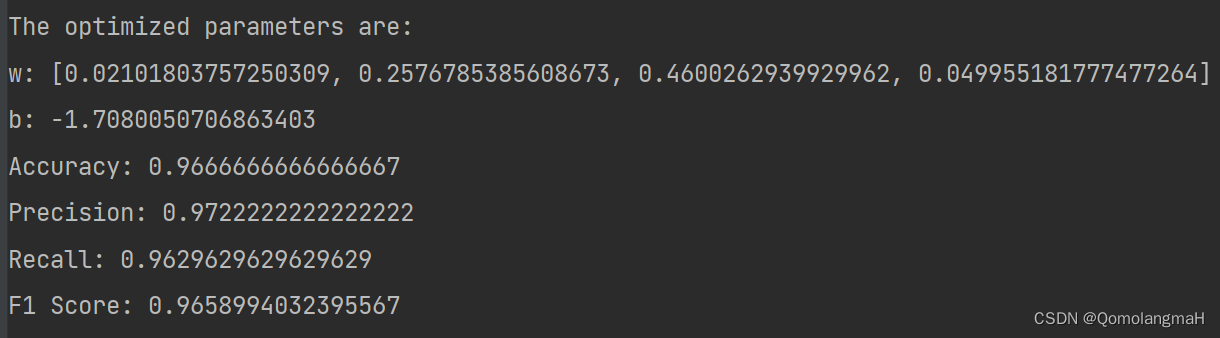
【深度学习实验】线性模型(五):使用Pytorch实现线性模型:基于鸢尾花数据集,对模型进行评估(使用随机梯度下降优化器)
目录 一、实验介绍 二、实验环境 1. 配置虚拟环境 2. 库版本介绍 三、实验内容 0. 导入库 1. 线性模型linear_model 2. 损失函数loss_function 3. 鸢尾花数据预处理 4. 初始化权重和偏置 5. 优化器 6. 迭代 7. 测试集预测 8. 实验结果评估 9. 完整代码 一、实验介…...
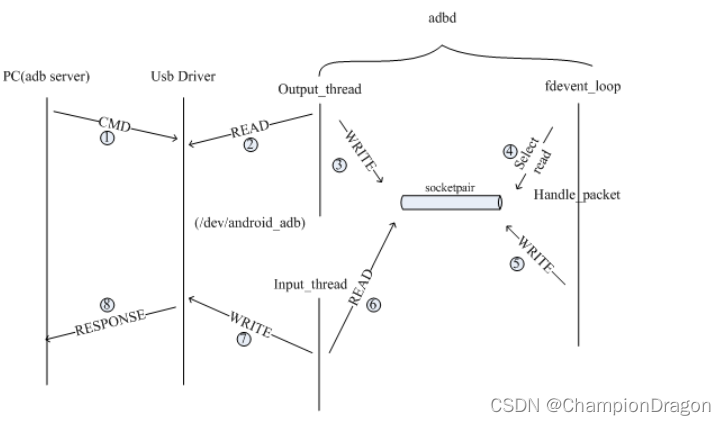
ADB底层原理
介绍 adb的全称为Android Debug Bridge,就是起到调试桥的作用。通过adb我们可以在Eclipse/Android Studio中方便通过DDMS来调试Android程序,说白了就是debug工具。adb是android sdk里的一个工具, 用这个工具可以直接操作管理android模拟器或者真实的and…...

etcd之读性能主要影响因素
1、Raft模块-线性读ReadIndex-节点之间的RTT延时、磁盘IO 线性读时Follower节点首先会向Raft 模块发送ReadIndex请求,此时Raft模块会先向各节点发送心跳确认,一半以上节点确认 Leader 身份后由leader节点将已提交日志索引 (committed index) 封装成 Rea…...
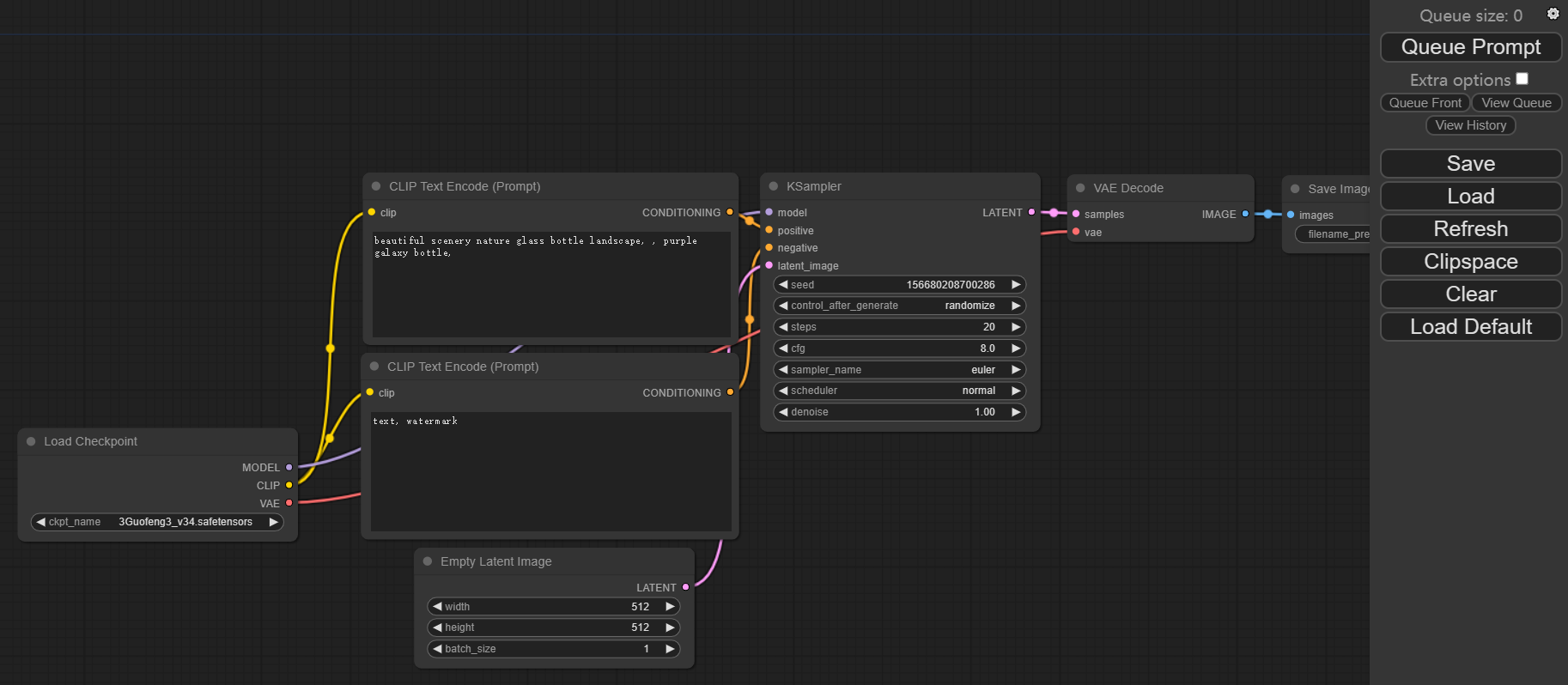
【Stable Diffusion】安装 Comfyui 之 window版
序言 由于stable diffusion web ui无法做到对流程进行控制,只是点击个生成按钮后,一切都交给AI来处理。但是用于生产生活是需要精细化对各个流程都要进行控制的。 故也就有个今天的猪脚:Comfyui 步骤 下载comfyui项目配置大模型和vae下载…...
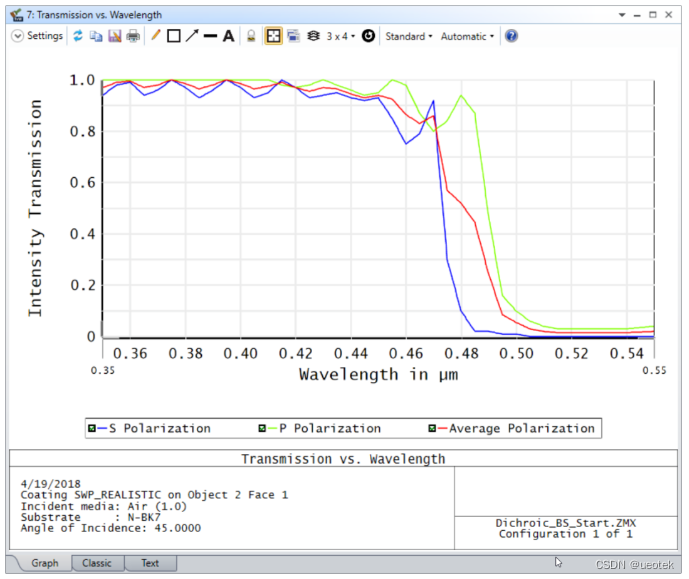
Ansys Zemax | 如何建立二向分色分光镜
分光镜(Beam splitter)可被运用在许多不同的场合。一般而言,入射光抵达二向分色分光镜(dichroic beam splitter)时,会根据波长的差异产生穿透或反射的现象。这篇文章将说明如何在OpticStudio的非序列模式(non-sequential mode)中建立二向分色分光镜&…...
Mybatis学习笔记8 查询返回专题
1.返回实体类 2.返回List<实体类> 3.返回Map 4.返回List<Map> 5.返回Map<String,Map> 6.resultMap结果集映射 7.返回总记录条数 新建模块 依赖 目录结构 1.返回实体类 如果返回多条,用单个实体接收会出异常 2.返回List<实体类> 即使返回一条记…...
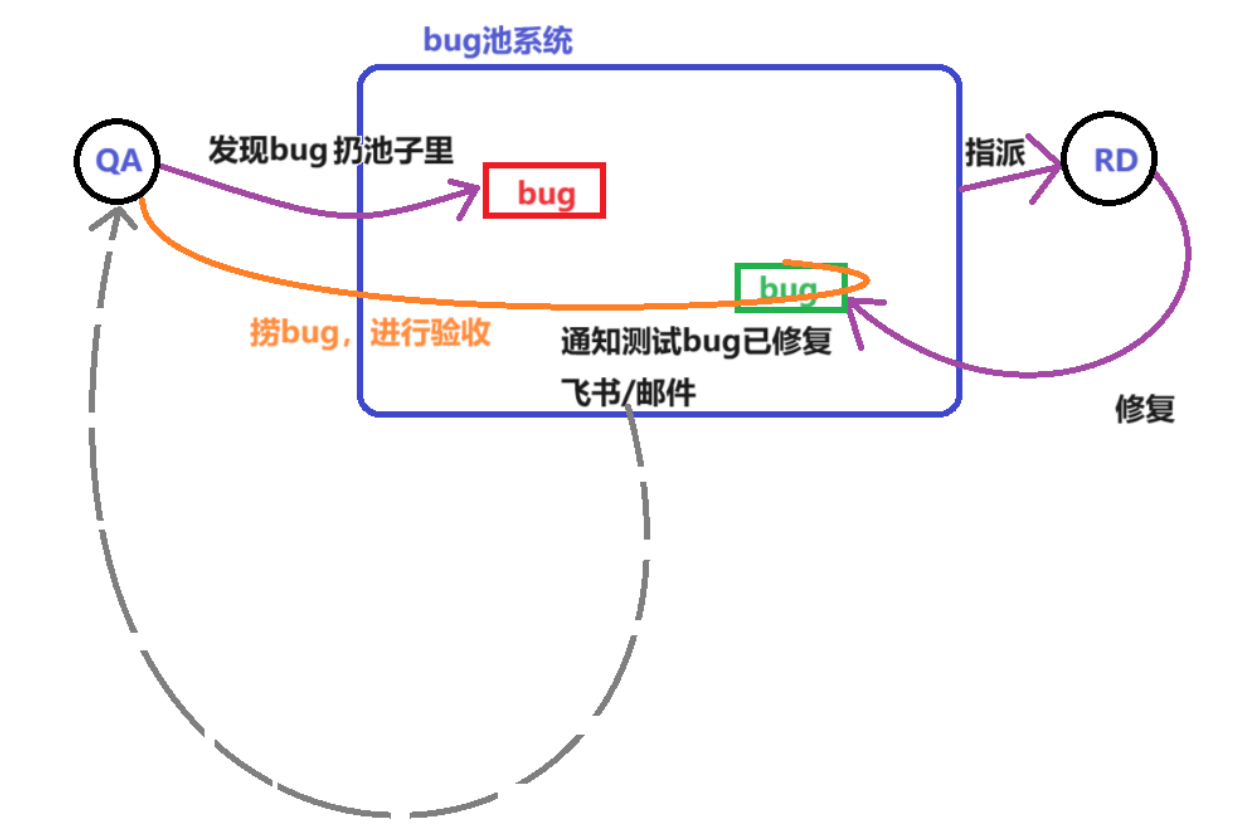
【测试开发】基础篇 · 专业术语 · 软件测试生命周期 · bug的描述 · bug的级别 · bug的生命周期 · 处理争执
【测试开发】基础篇 文章目录 【测试开发】基础篇1. 软件测试生命周期1.1 软件生命周期1.2 软件测试生命周期 2. 描述bug3. 如何定义bug的级别3.1 为什么要对bug进行级别划分3.2 bug的一些常见级别 4. bug的生命周期5. 产生争执这么怎么办(处理人际关系)…...

bing许少辉乡村振兴战略下传统村落文化旅游设计images
bing许少辉乡村振兴战略下传统村落文化旅游设计images...

第三十一章 Classes - 继承规则
第三十一章 Classes - 继承规则 继承规则 与其他基于类的语言一样,可以通过继承组合多个类定义。 类定义可以扩展(或继承)多个其他类。这些类又可以扩展其他类。 请注意,类不能继承 Python 中定义的类(即 .py 文件中…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
