9.18算法
机器人重物1126
注意编号是方块的,而不是格点的
及如果为n*m的矩阵,需要开(n+1)*(m+1)的矩阵
//如果没有转向,就是走迷宫,结合记忆化,如果这个点之前走过就不走了
//又转向的话,就用一个变量记录当前转向,
//然后每次转向就花费以此,这时直接bfs就不一定是最优解
void change() {for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (sd[i][j] == 1) {//每个点本身就是确定的方块中的一个位置a[i - 1][j] = 1;a[i][j - 1] = 1;//共需要让4个位置置1,即一个方块的四个点a[i - 1][j - 1] = 1;a[i][j] = 1;}}}
}
void fxto() {switch (ch[0]) {case'N':cto = 1; break;}
}
//ft[i]表顺时针排列各个方向的编号
//用顺时针表示并不是说只能顺时针旋转,只是用顺时针表示顺序
//每次都可以向左或向右(即顺&逆)
int ft[5] = { 0,1,4,2,3 };
//fft表示数字i在ft数组中的下标,即要先目标为i的方向,需要用ft数组中的哪个
int fft[5] = { 0,1,3,4,2 };
int abs[5]={0,5}
node first;
first.x = x11, firxt.y = y11;
fxto();
first.t = cto;
first.time = 0;
q.push(first);
node u, d;
while (!q.empty()) {u = q.front();q.pop();//u.t代表实际方向,i是这个方向顺时针旋转i次for (int i = 1; i <= 4; i++) {//表示这个方向顺时针起手的第i个方向int zhuan = abc[i];//转到这第i个方向所需要的最少次数(可以向左也可以向右)int fangx = fft[u.t] + i;//全当成顺时针旋转,这个点顺时针起手的第i个方向//当i确定时,下个方向也就确定了//然后zhuan就是通过abc数组确定,通过去周期得到转后的方向if (fangx == 5)fangx = 1;if (fangx == 6)fangx = 2;if (fangx == 7)fangx = 3;if (fangx == 8)fangx = 4;fangx = ft[fangx];for (int j = 1; j <= 3; j++) {int lsx = u.x + fx[fangx] * j;int lsy = u.y + fy[fangx] * j;if (lsx >= n || lsx <= 0 || lsy >= m || lsy <= 0 || (lsx == x11 && lsy == y11) || a[lsx][lsy] == 1) {break;}//每次都是距离比当前记录最小才更新目标点的值(目标点记录到达该点的最小值)//只有比其小,才更新}}小木棍1120
如果让两个最小的相加,那么总会剩出最大的组合在一起,从而使最长木棍变长
注意木棍长度相同,要让这个相同的长度最短
?那怎么求相同的长度?
介于两个最长和最短的长度之间
就是说原始木棍的长度*原始木棍的数量=现在木棍的长度和
只需要枚举到木棍长度和的一半即可,因为此时所有木棍有可能拼成2根木棍,原始长度再大就只能是所有木棍拼成1根,因为原始木棍长度=现在木棍长度和/原始木棍数量(>=1),而为1时必不为最短长度,故只需要遍历到1半即可
先在dfs外定原始棍子的长度
dfs(k,last,rest)k表示正在拼接第几根原来的木棍,
长度相同时也可以拼接成原始木棍,是说如果用相同木棍拼不成时,再往后,用下个更短的木棍
预处理是说排序后重复元素很多,然后要不用与当前木棍长度相同的木棍
如果当前木棍的剩余长度等于当前木棍长度或原始长度
inline int read() {int x = 0; bool f = 1; char c = getchar();for (; !isdigit(c); c = getchar()) if (c == '-') f = 0;for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - '0';if (f) return x;return 0 - x;
}
void dfs(int k, int last, int rest) {//k为目前正在拼接的原始棍子的编号,last为正在拼的木棍的前一节编号,rest为剩下的长度int i;if (!rest) {if (k == m) {ok = 1; return;}//每次开拼都是从剩下的最长里选一个for (i = 1; i <= cnt; i++) {if (!used[i]) { break; }}//找到第一个没有用过的棍子,由于从左到右遍历,此时就是剩下的最长的棍子used[i] = 1;dfs(k + 1, i, len - a[i]);//建立在前k个棍子是这样拼的基础上used[i] = 0;if (ok)return;}int l = last + 1, r = cnt, mid;//二分找last后第一个,木棍长度不大于剩余长度rest的位置while (l < r) {mid = (l + r) >> 1;if (a[mid] <= rest)r = mid;else l = mid + 1;}for (i = l; i <= cnt; i++) {//找到后从第一个开始拼,每次都用可以用的最长的作为搜索起始条件if (!used[i]) {used[i] = 1;dfs(k, i, rest - a[i]);used[i] = 0;if (ok)return;//rest=a[i],在该层dfs中已经用过a[i],如果相等,那么那层dfs后直接这个棍子就拼好了//之后就是在那个棍子拼好后接着往下拼,这是后续所有情况的最优情况,//如果没ok,if (rest == a[i] )return;//如果剩下的长度和当前的木棍(第一个不大于rest的木棍长度一样i = next[i];if (i == cnt)return;}}
}
n = read();
int d;
for (int i = 1; i <= n; i++) {d = read();if (d > 50)continue;a[++cnt] = d;sum += d;
}
sort(a + 1, a + cnt + 1, cmp);
next[cnt] = cnt;
for (int i = cnt - 1; i > 0; i--) {if (a[i] == a[i + 1]) {next[i] = next[i + 1];//由于是从后往前赋值,所以相同时就记录前一个所记录的编号}//是因为从后往前赋值,所以重复元素总存在一个最右边的元素和下一个不重复元素相邻else {next[i] = i;//不相同时才记录编号}
}
for (len = a[1]; len <= sum / 2; len++) {//让len成为原始长度if (sum % len != 0)continue;m = sum / len;//得到原始棍子的数量ok = 0;used[1] = 1;//第一个棍子总要用的dfs(1, 1, len - a[1]);used[1] = 0;//回溯,试试下个棍子,下个长度前,先把1给回溯了if (ok) {cout << len;return 0;//由于len是从小遍历到大,所以最先ok的就是最短的len}
}放梅花5521
要在某个位置放花,就要这个结点下的所有孩子结点都有花
第i个整数pi代表第i+1号节点的家长节点编号,数组下标i 确定节点的位置,所记录的值代表家长的位置
要想孩子节点有花,先得孩子节点的节点得有花,如果要在第i个孩子位置插花,那么必须满足前i个孩子节点的要求,就是说前面的孩子位置必须要有花,而且在前面孩子位置有花的基础上,还得有当前位置所需要的花
必然存在一种排序可以使所需要的花的数量最小
想法应该是让节点上所需的花的最小的排在前面,以及孩子的孩子所需花最多的排在前面(如果排在后面,在前面已经有了很多花(要保持)的基础上,还额外需要很多的花来装这个节点,如果在前面就装好了,就不需要了)就是说最小的花数至少应该要满足插每个节点的需求,但是因为插完之后要保持(即插后续的花在之前已经插过的基础上),那么最小的花数就必定大于每个节点的需求,
而且也不是单纯的让代价由低到高排好就行,因为要考虑到插每个位置时还需要额外考虑每个位置的孩子花数(假设这个节点装的中等,但是孩子多,虽然孩子是必不可少的,但是把它放在前面就可能比把它放在后面好,放在后面不仅要准备必不可少的孩子,还要准备这期间所增加的额外负担,
就是这么想,音量,每点一首歌基础音量就增加一点(积累的前面节点的负担),然后每首歌都固定有一个最高声音(装这个节点时的需要),但是放完后就下来了,目的就是要让最大音量小(防止爆表),如果点完后提高基础音量大的,就应该放在后面(但如果放它的音量很高,就需要考虑一下,到底是放在后面(即已经提高了很高基础音量之后突然爆破)的声音大,还是提前放,让所有歌都在已经提高了基础音量后再结合其自身的一个最高声音大
可以发现,一首歌既然已经放完,那么其在放完的序列中的顺序就无所谓了,因为都已经提高过了,也就是说对于第i,i+1的歌,其之间排序对后续的歌所能达到的音量无关,只与这两首歌所能达到的音量有关,即要么在第i首歌放完后的基础上突然拔高第i+1的最高音量,要么在第i+1首歌放完后的基础上突然拔高第i首的最高音量,哪个所能达到的最高音量更低,就怎么排。
按照这样的排序,相当于冒泡(还是选择?),就是随便选一首歌,和它周围的歌比较,如果放在别的歌前面能使这二者
两者之中总有最大值,但不同排序下的最大值不一样,目的是让最大值更小,所以尝试交换双方的位置,从中选择一个最大值更小的去排(10,第i首,5,最高3,第i+1首,1,最高9,此时爆表音量为24,调整后为14,需要注意这两首过后,其次序就没意义了,因为都加到基础音量上了)
化简完最后就是如果第i首排在前面音量更小,那么b1-s1<b2-s2
如果第i+2首想排在原来的位置,就要保证bi+1-si+1<bi+2-si+2,不然就是第i+1位排到第i+2位上,而且如果第i+2位到第i+1位想稳住,就必须要大于bi-si,否则还会往后走,即选择排序的过程
这样排,是让每首歌都有最小的一个演奏音量,就是让整体的声音小下来,不知道当前这个歌是不是最吵的歌,就让它尽可能不吵,来一首歌就放一个合适的位置
疑惑就是疑惑为什么最后的不是max,为什么不把max放在最前面,需要考虑到最大的还有基础音量
在求爆表的最大音量,并不一定就是最后一位最大,因为如果有首歌它的最大音量很大很大,那么按照规则,就会被排到很靠前的位置,但演这首歌依然需要很大的音量,所以即使这首歌在前面的位置,爆表音量最大值也是他的,就是维护一个最大值,然后遍历每个位置,遍历(遍历时就是已经排好序的)过了就表示这首歌已经放了,然后不断求这个歌放时的最大音量,和记录的最大音量比较,维护一个最大的音量
国王游戏1080
同理,每次值为前面记录的积和当下的除,每个人都要在前面的基础上乘上自己的因子为自己的奖赏,即(a/b),前面人过了就积累基础为a,相当于提高基础音量和每首歌自己有个音量
有一个位置,位置是这个位置,区别只在于谁上了这个位置,谁上的时候最小
这么想,对于最大的所在的那个位置,总有四个值,即直接在前面的基础上演奏,以及提高最大的基础后演奏后一首,和在前面的基础上演奏后一首,以及提高后一首的基础上演奏最大的,如果后一首是更大的
max(w+s1,w+b1+s2)<max(w+s2,w+b2+s1)
如果s1>b1+s2(第一首放的音量比在第一首基础上放的第二首还大),max=s1那么b2+s1>s2,即最大的一首放前面,那么交换后的最大音量(在第二首的基础上放第一首)一定比交换前的最大音量(第一首直接放)大
为什么最大的一首不继续往前走了?
说明max(w+s0,w+b0+s1)<max(w+s1,w+b1+s0)
前者是在前面一首直接放和在前面一首的基础上放最大的
后者是最大的直接放,和在最大的基础上放第一首
依然考虑说放最大的时候最大,由于前面max小于后面,
如果交换的话,对后面没影响,但是在最大那首的基础上就成了最大的了,而且比最大的时候还要大
(排在前面,要么基础音量小,要么爆表音量大)
能交换的条件是放在后面得到的最大值更小,如果w+s1就是最大值,那么就不需要交换,因为交换后最大值为b2+s1,更大了
至于前面,就是如果后面是最大值即b1+s2,交换后肯定比s2大,那就需要比较b2+s1,此时主体就变了,就需要比较到底谁在这个位置(你有我的基础后大还是我有你的基础后发挥更大)的最大值更小,然后选更小的在这里
如果前面大,就是必要项占据了主导地位(相比基础项),如果后面大,就是基础项占据了主导地位(然后就排序,看谁先提供这个基础才能使最大值更小)
皇后游戏2123
前面大臣所获奖金数和前面左手上数和的最大值,再加上右手上数
右手上数可以看成必须的,变的就是前面的基础项
基础项取决于前面的值和左手上数,
如果不取max的话,就是左手上数和和右手上数和
?排序规则怎么确定?
前两道给出了基础项的明确计算方法,且唯一,现在的话就难判断四项的关系,相邻的两项看不出来,交叉的,放在前面肯定比放在后面少,因为后面有前面的基础
对于相邻两项,如果前面的更大,那么就不要交换,如果后面更大(就是说在前面有基础补足的情况下与必要项的和更大),肯定比交换后的第一项大,那么就和第二项比较(在后面的基础上用前面的必要项)
但是这是在已经排好前面的前提条件下,可是实际是不知道前面的是什么状况,也不能保证现在这俩的位置会不会对后面的排序造成影响
相关文章:

9.18算法
机器人重物1126 注意编号是方块的,而不是格点的 及如果为n*m的矩阵,需要开(n1)*(m1)的矩阵 //如果没有转向,就是走迷宫,结合记忆化,如果这个点之前走过就不走了 //又转向的话,就用一个变量记录当前转向&…...

【Spring Bean的生命周期】
文章目录 Spring Bean的生命周期实例化构造器实例化工厂方法实例化 属性赋值XML方式注解方式 初始化postProcessBeforeInitialization()和postProcessAfterInitialization()InitializingBean接口的afterPropertiesSet()方法通过Bean注解定义的初始化方法使用PostConstruct注解标…...

信息化发展49
软件设计 1 、软件设计是需求分析的延伸与拓展。需求分析阶段解决“做什么” 的问题,而软件设计阶段解决“怎么做” 的问题。同时, 它也是系统实施的基础, 为系统实施工作做好铺垫。合理的软件设计方案既可以保证系统的质量, 也可…...

linux常用命令(4):mkdir命令(创建目录)
文章目录 一、命令简介二、命令格式三、常用示例 一、命令简介 mkdir(make directories)创建目录。 若指定目录不存在则创建目录。若指定目录已存在,则会提示已存在而不继续创建。 touch与mkdir的区别? 很多人可能会把这个搞混淆ÿ…...
企业架构LNMP学习笔记58
开始学习Tomcat: 学习目标和内容: 1)能够描述Tomcat的使用场景; 2)能够简单描述Tomcat的工作原理; 3)能够实现部署安装Tomcat; 4)能够实现和配置Tomcat的Server服务…...
[JAVAee]SpringBoot配置文件
配置文件的介绍 配置文件当中记录了许多重要的配置信息,例如: 数据库的连接信息(用户的账户与密码)项目的启动端口第三方系统的调用密匙用于记录问题产生的日志 在spring框架中一些特定的框架会自动调用配置文件中的配置信息来运用. 配置文件中的属性也起到了类似全局变量的…...

复制远程连接到Linux使用VIM打开的内容到Windows
我们经常是使用SSH工具远程连接到Linux服务器上进行工作,有时候需要将Linux下使用VIM打开的文件内容复制到Windows上来,默认情况下,可能会复制不了,因为VIM默认情况下是使用的set mousea的设置,它会让鼠标选中的时候进…...

左神算法之中级提升班(9)
目录 【案例1】 【题目描述】 【思路解析】 【代码实现】 【案例2】 【题目描述】 【思路解析 平凡解技巧 从业务中分析终止条件 重点】 【代码实现】 【案例3】 【题目描述】 【思路解析】 【案例4】 【题目描述】 【思路解析】 【代码实现】 【动态规划代码】…...

SmartNews 基于 Flink 的 Iceberg 实时数据湖实践
摘要:本文整理自 SmartNews 数据平台架构师 Apache Iceberg Contributor 戢清雨,在 Flink Forward Asia 2022 实时湖仓专场的分享。本篇内容主要分为五个部分: SmartNews 数据湖介绍基于 Icebergv1 格式的数据湖实践基于 Flink 实时更新的数据…...

websocket请求通过IteratorAggregate实现流式输出
对接国内讯飞星火模型,官方文档接口采用的是websocket跟国外chatgpt有些差异。 虽然官网给出一个简单demo通过while(true),websocket的receive()可以实现逐条接受并输出给前端,但是通用和灵活度不高。不能兼容现有项目框架的流式输出。故模仿…...

《C和指针》笔记28:可变参数和stdarg宏
可变参数列表可以通过宏来实现,这些宏定义于stdarg.h头文件,它是标准库的一部分。这个头文件声明了一个类型va_list和三个宏——va_start、va_arg和va_end 。我们可以声明一个类型为va_list的变量,与这几个宏配合使用,访问参数的值…...
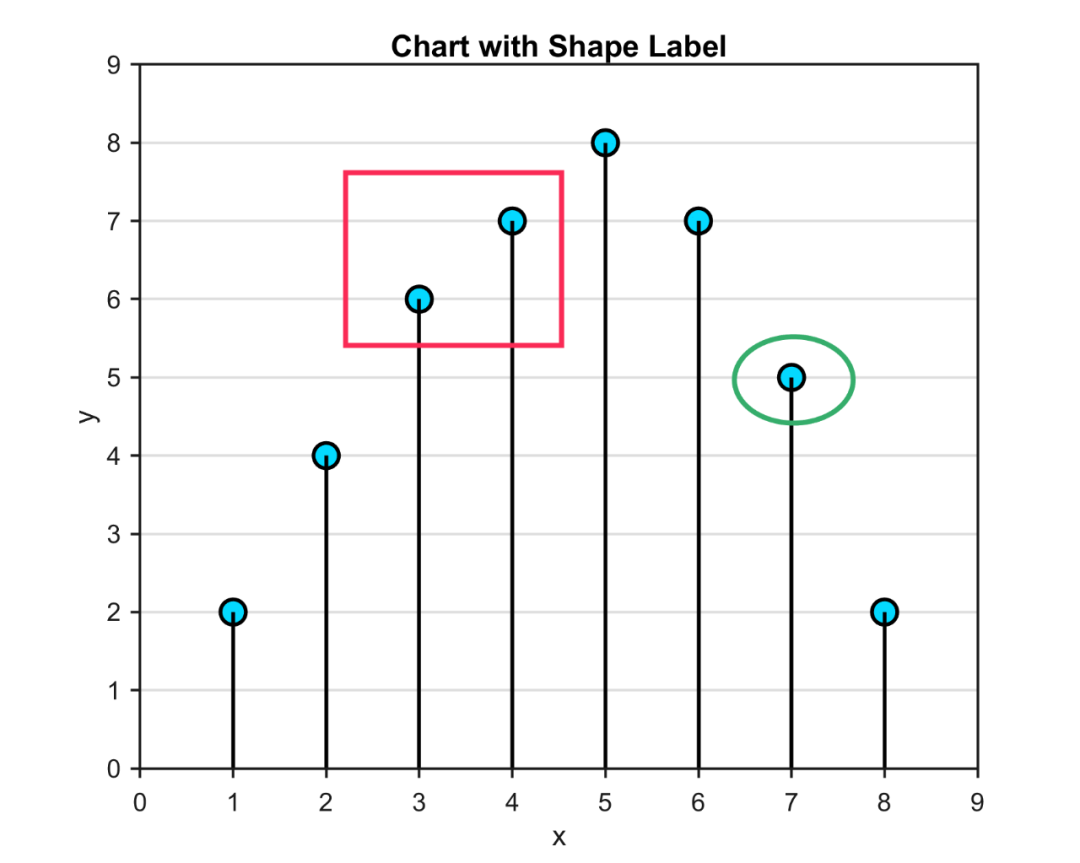
Matlab论文插图绘制模板第114期—带图形标记的图
之前的文章中,分享了Matlab带线标记的图: 带阴影标记的图: 带箭头标记的图: 进一步,分享一下带图形标记的图,先来看一下成品效果: 特别提示:本期内容『数据代码』已上传资源群中&…...

Python:用于有效对象管理的单例模式
1. 写在前面 在本文中,我们将介绍一种常用的软件设计模式 —— 单例模式。 通过示例,演示单例创建,并确保该实例在整个应用程序生命周期中保持一致。同时探讨它在 Python 中的目的、益处和实际应用。 关键点: 1、单例模式只有…...
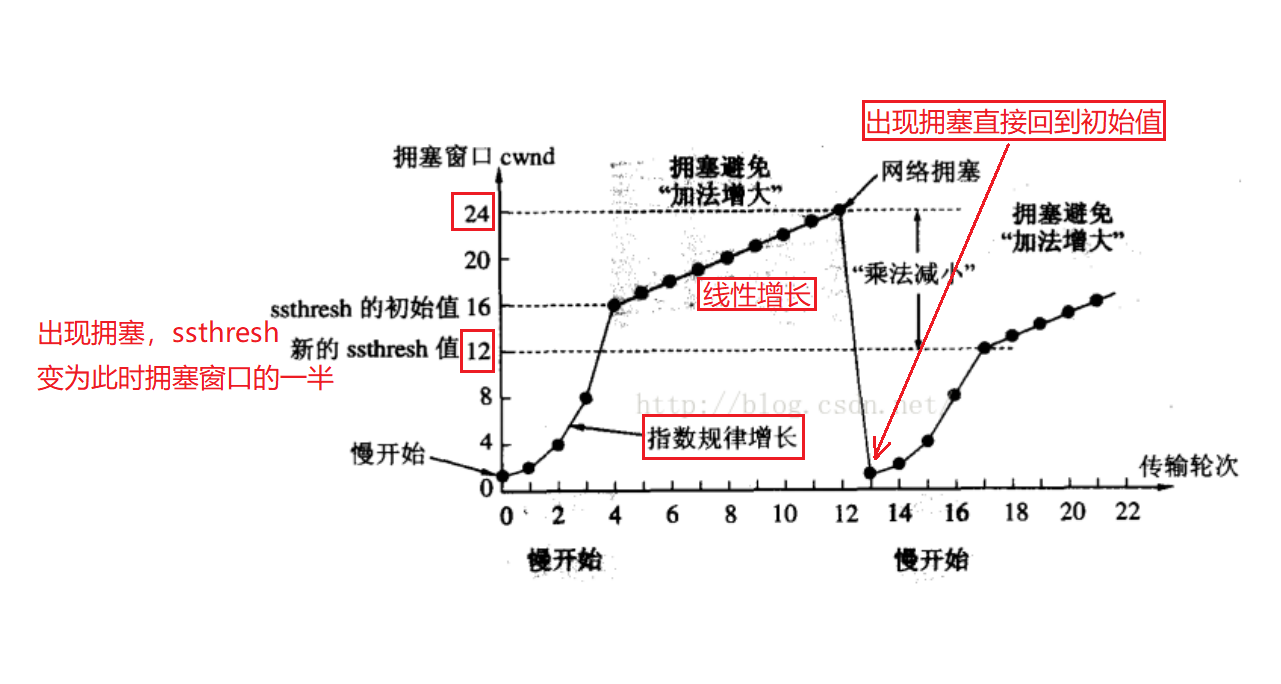
【TCP】滑动窗口、流量控制 以及拥塞控制
滑动窗口、流量控制 以及拥塞控制 1. 滑动窗口(效率机制)2. 流量控制(安全机制)3. 拥塞控制(安全机制) 1. 滑动窗口(效率机制) TCP 使用 确认应答 策略,对每一个发送的数…...
)
Xilinx FPGA管脚约束语法规则(UCF和XDC文件)
文章目录 1. ISE环境(UCF文件)2. Vivado环境(XDC文件) 本文介绍ISE和Vivado管脚约束的语句使用,仅仅是管脚和电平状态指定,不包括时钟约束等其他语法。 ISE使用UCF文件格式,Vivado使用XDC文件&…...

服务网格和CI/CD集成:讨论服务网格在持续集成和持续交付中的应用。
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

代码随想录训练营第56天|583.两个字符串的删除操作,72.编辑距离
代码随想录训练营第56天|583.两个字符串的删除操作,72.编辑距离 583.两个字符串的删除操作文章思路代码 72.编辑距离文章思路代码 总结 583.两个字符串的删除操作 文章 代码随想录|0583.两个字符串的删除操作 思路 如果不按照编辑距离考虑的话,只需要…...

【JDK 8-Lambda】3.1 Java高级核心玩转 JDK8 Lambda 表达式
一、 什么是函数式编程 ? 二、 什么是lambda表达式? 1. 先看两个示例 A.【创建线程】 B.【数组排序-降序】 2. lambda表达式特性 A. 使用场景(前提): B. 语法 (params) -> expression C. 参数列表 D. 方法体 F. 好处 一、 什么是函数式编…...

【C#】XML的基础知识以及读取XML文件
最近在学读取文件 目录 介绍特点结构XML的语法规则XML 命名规则 C#操作XML新建读取第一种第二种第三种 读取属性 介绍 XML (可扩展标记语言,eXtensible Markup Language) 是一种标记语言,它被设计用来传输和存储数据。 特点 可扩展性:由于…...

Immutable.js简介
引子 看一段大家熟悉的代码 const state {str: wwming,obj: {y: 1},arr: [1, 2, 3] } const newState stateconsole.log(newState state) // truenewState和state是相等的 原因: 由于js的对象和数组都是引用类型。所以newState的state实际上是指向于同一块内存…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
