数据结构——排序算法——冒泡排序
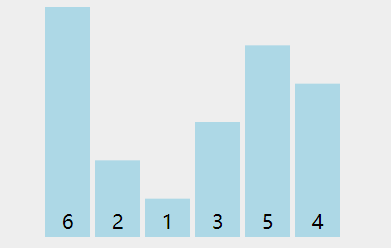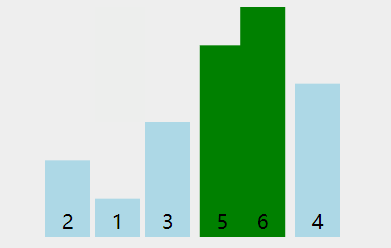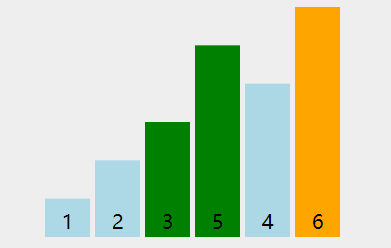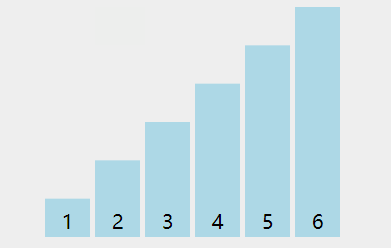
冒泡排序1
void swap(vector<int> arr, int i, int j)
{int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}void bubbleSort1(vector<int> arr)
{for (int i = 0; i < arr.size() - 1; i++){for (int j = 0; j < arr.size() - 1 - i; j++){if (arr[j] > arr[j + 1]){// 如果左边的数大于右边的数,则交换,保证右边的数字最大swap(arr, j, j + 1);}}}
}
冒泡排序2
void bubbleSort2(vector<int> arr)
{//初始时 swapped 为 true ,省则则排序过程无法法启动bool swapped = true;for (int i = 0; i < arr.size() - 1; i++) {// 如果没有发生过交换,说明剩余部分已经有序,排序完成if (!swapped)break;// 设置 swapped 为 false,如果发生交换,则将其置为 trueswapped = false;for (int j = 0; j < arr.size() - 1 - i; j++) {if (arr[j] > arr[j + 1]) {// 如果左边的数大于右边的数,则交换,保证右边的数字最大swap(arr, j, j + 1);// 表示发生了交换swapped = true;}}}
}冒泡排序3
void bubbleSort3(vector<int> arr)
{bool swapped = true;// 最后一个没有经过排序的元素的下标int indexOfLastUnsortedElement = arr.size() - 1;// 上次发生交换的位置int swappedIndex = -1;while (swapped){swapped = false;for (int i = 0; i < indexOfLastUnsortedElement; i++){if (arr[i] > arr[i + 1]) {// 如果左边的数大于右边的数,则交换,保证右边的数字最大swap(arr, i, i + 1);// 表示发生了交换swapped = true;// 更新交换的位置swappedIndex = i;}}// 最后一个没有经过排序的元素的下标就是最后一次发生交换的位置indexOfLastUnsortedElement = swappedIndex;}
}
相关文章:

数据结构——排序算法——冒泡排序
冒泡排序1 void swap(vector<int> arr, int i, int j) {int temp arr[i];arr[i] arr[j];arr[j] temp;}void bubbleSort1(vector<int> arr) {for (int i 0; i < arr.size() - 1; i){for (int j 0; j < arr.size() - 1 - i; j){if (arr[j] > arr[j 1…...

vscode使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:…...

python经典百题之求前!的和
题目:求12!3!…20!的和 方法一: 使用for循环和阶乘函数计算每项的值,再将每项的值累加起来。 def factorial(n):if n 0:return 1else:return n * factorial(n-1)sum 0 for i in range(1, 21):sum factorial(i) * iprint(sum)优点&#…...
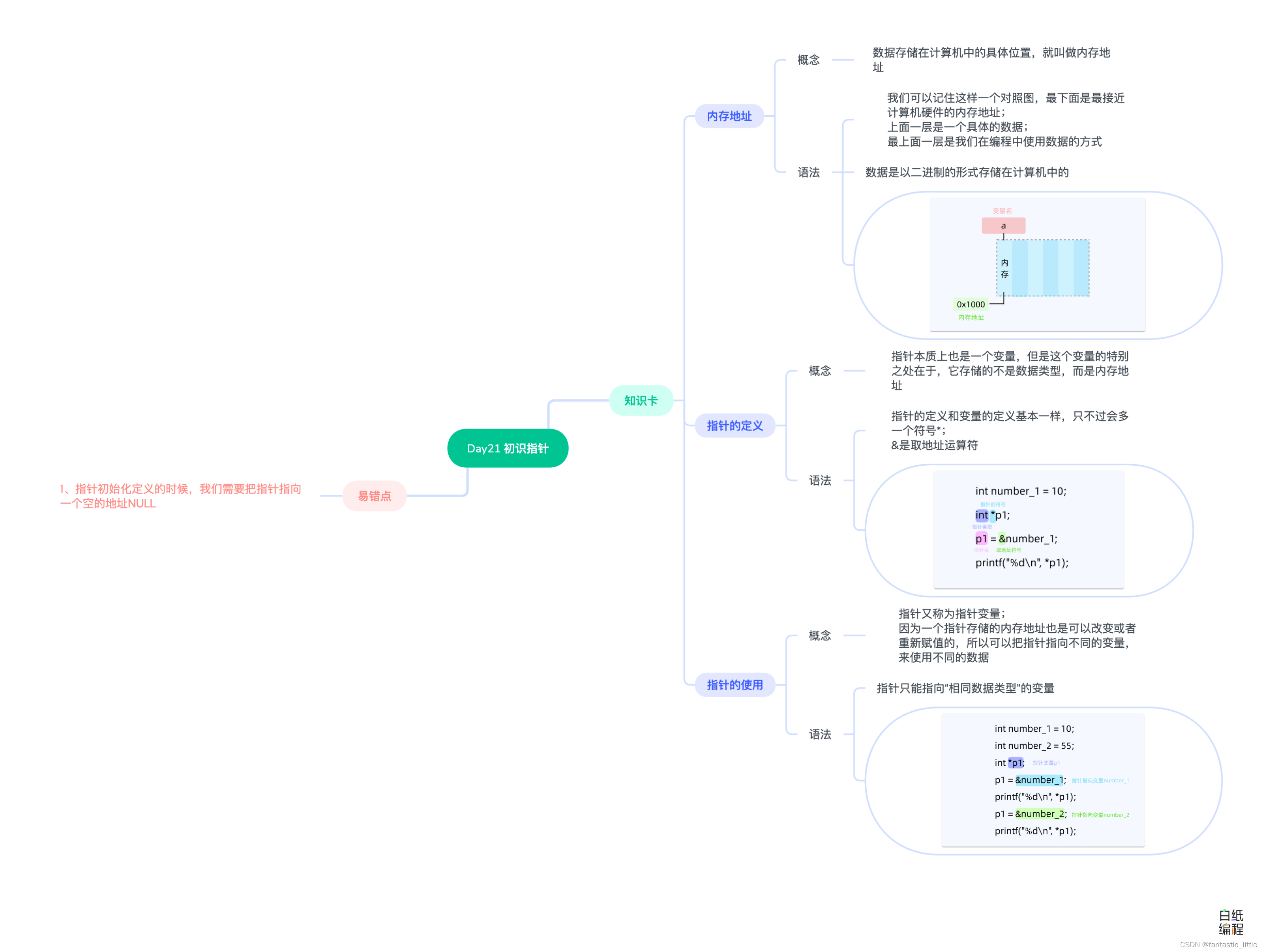
C语言入门Day_22 初识指针
目录 前言: 1.内存地址 2.指针的定义 3.指针的使用 4.易错点 5.思维导图 前言: 之前我们学过变量可以用来存储数据,就像一个盒子里面可以放不同的球一样。 这是一个方便大家理解专业概念的比喻。 在计算机世界里面,数据实…...
【面试必刷TOP101】删除链表的倒数第n个节点 两个链表的第一个公共结点
目录 题目:删除链表的倒数第n个节点_牛客题霸_牛客网 (nowcoder.com) 题目的接口: 解题思路: 代码: 过啦!!! 题目:两个链表的第一个公共结点_牛客题霸_牛客网 (nowcoder.com) …...
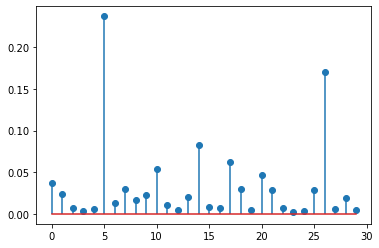
手刻 Deep Learning -第壹章 -PyTorch教学-激励函数与感知机入门(上)
一、前言 本文接续前篇教学 Pytorch 与线性回归 ,本文着重在 Activation Function ( 中文称 激励函数 ),我们会介绍激励函数 (也有人称 激活函数? 激发函数? ) 为什么会有用…...
物理内存分配
目录 内核物理内存分配接口 内存分配行为(物理上) 内存分配的行为操作 内存 三个水位线 水线计算 水位线影响内存分配行为 内存分配核心__alloc_pages 释放页 1、内核物理内存分配接口 struct page *alloc_pages(gfp_t gfp, unsigned int ord…...
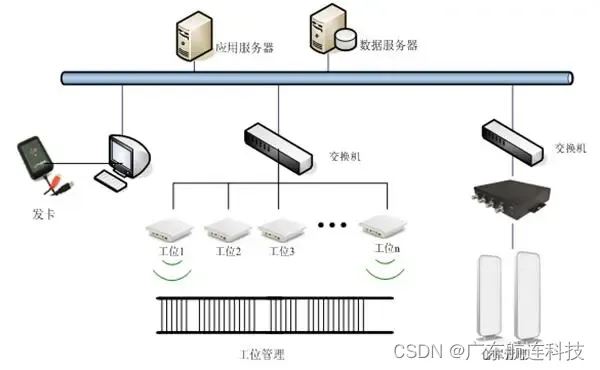
RFID产线自动化升级改造管理方案
应用背景 在现代制造业中,产线管理是实现高效生产和优质产品的关键环节,产线管理涉及到生产过程的监控、物料管理、工艺控制、质量追溯等多个方面,有效的产线管理可以提高生产效率、降低成本、改善产品质量,并满足市场需求的变化…...

全量数据采集:不同网站的方法与挑战
简介 在当今数字化时代中,有数据就能方便我们做出很多决策。数据的获取与分析已经成为学术研究、商业分析、战略决策以及个人好奇心的关键驱动力。本文将分享不同网站的全量数据采集方法,以及在这一过程中可能会遇到的挑战。 部分全量采集方法 1. 撞店…...

Redis——渐进式遍历和数据库管理命令
介绍 如果使用keys * 这样的操作,将Redis中所有的key都获取到,由于Redis是单线程工作,这个操作本身又要消耗很多时间,那么就会导致Redis服务器阻塞,后续的操作无法正常执行 而渐进式遍历,通过多次执行遍历…...

如何打造可视化警务巡防通信解决方案
近年来,科学技术飞速发展,给予了犯罪分子可乘之机。当面临专业化的犯罪分子、高科技的犯罪手段,传统警务模式似乎不能满足警方打击犯罪的需要,因此当今公安工作迫切需要构建智能化、系统化、信息化的警务通信管理模式。 警务人员…...

ATF(TF-A) SPMC威胁模型-安全检测与评估
安全之安全(security)博客目录导读 ATF(TF-A) 威胁模型汇总 目录 一、简介 二、评估目标 1、数据流图 三、威胁分析 1、信任边界 2、资产 3、威胁代理 4、威胁类型 5、威胁评估 5.1 端点在直接请求/响应调用中模拟发送方或接收方FF-A ID 5.2 篡改端点和SPMC之间的…...

BIO AIO NIO 的区别
BIO AIO NIO 是 Java 中用于 I/O 操作的三种不同的编程模型。它们的区别在于它们执行I/O 操作的方式和效率。在讲 BIO,NIO,AIO 之前先来回顾一下这样几个概念:同步与异步,阻塞与非阻塞。 同步与异步 同步:同步就是发起一个调用后ÿ…...
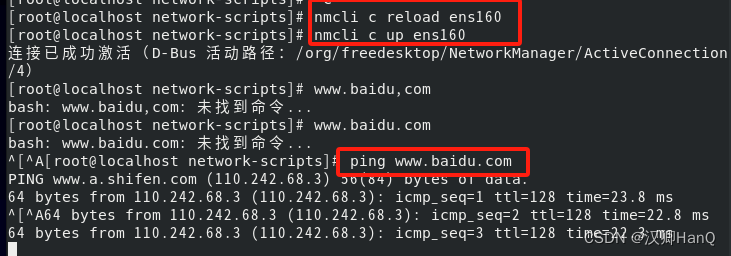
大数据学习1.1-Centos8网络配置
1.查看虚拟网卡 2.配置网络信息 打勾处取消 记住箭头的数字 3.修改 网络连接 4.进入虚拟网络 5.进入属性 6.修改IPv4 5.将iIP和DNS进行修改 6.配置网络信息-进入修改网络配置文件 # 进入root用户 su root # 进入网络配置文件 cd /etc/sysconfig/network-scripts/ # 修改网络配…...

在Android studio 创建Flutter项目运行出现问题总结
在Android studio 中配置Flutter出现的问题 A problem occurred configuring root project ‘android’出现这个问题。解决办法 首先找到flutter配置的位置 在D:\xxx\flutter\packages\flutter_tools\gradle位置中的flutter.gradle buildscript { repositories { googl…...
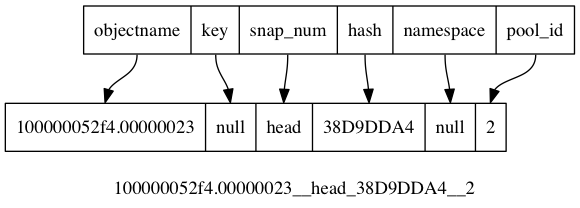
Ceph入门到精通-ceph对于长文件名如何处理
RADOS object with short name 上一篇博文,我们将介绍了对象相关的数据结构ghobject_t,以及对象在底层文件系统存储的文件名,以及如何从文件名对应到 ghobject_t对象。 映射关系如下图所示: 这里面有一个漏洞,即obje…...

vue+element-ui 项目实战示例详解【目录】
vue 和 element是两个流行的前端即时,通常用于管理后台,PC等页面 能够快速构建美观的界面 1. vue2 介绍 Vue.js是一个流行的JavaScript框架,用于构建用户界面。它的版本分为Vue 2和Vue 3,而Element是一个基于Vue.js 2的UI组件库。…...
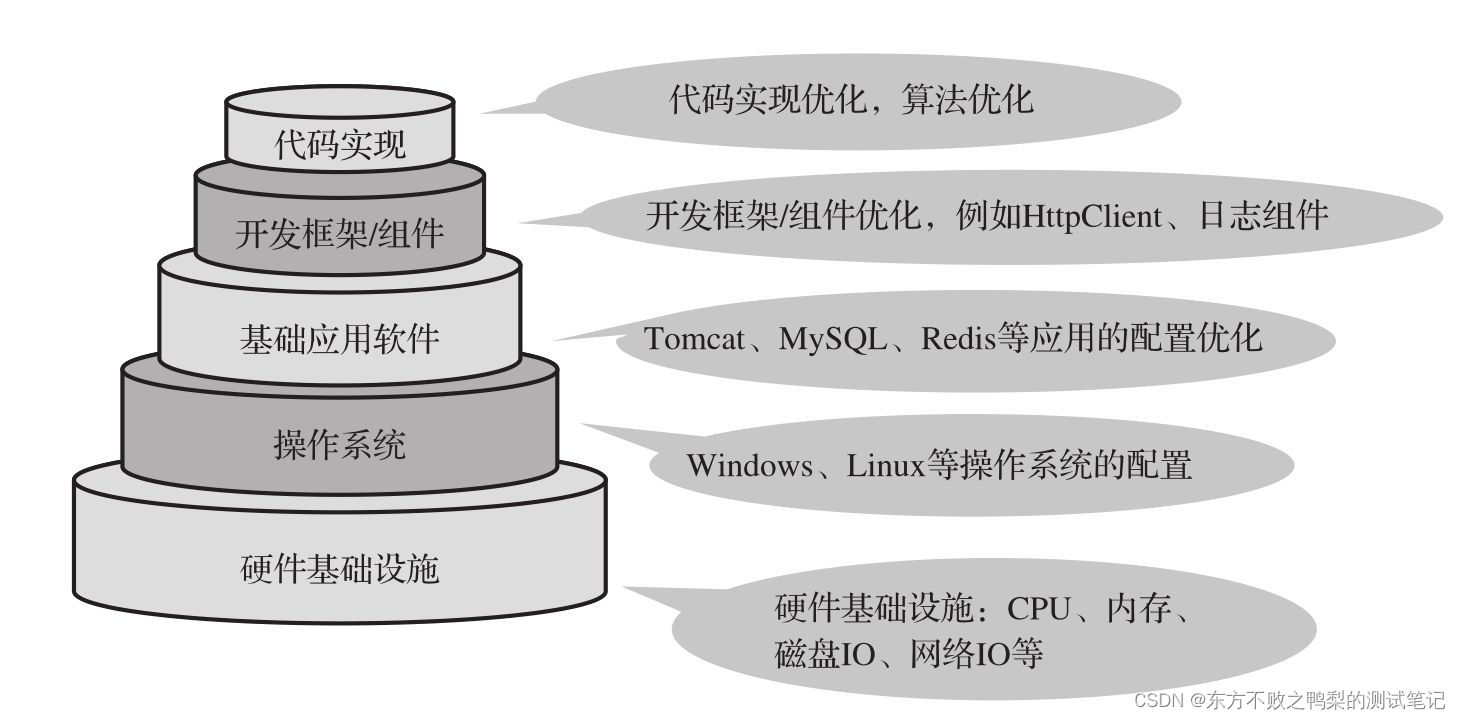
性能测试-性能调优主要方向和原则(15)
性能调优主要方向明确性能瓶颈之后,就需要进行性能调优了,调优主要从图所示的多个方向入手。能优化手段并不一定是独立应用的,在一次优化过程中很可能应用了多种优化技巧。 硬件层面优化 硬件层面优化更偏向于监控,当定位到硬件资源成为瓶颈后,更多是采用扩容等手段来解决…...
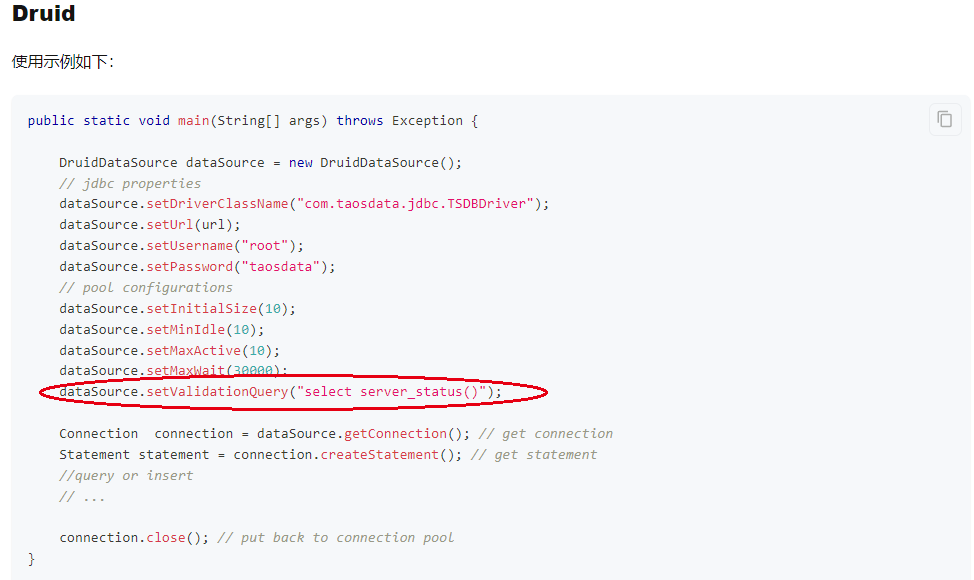
关于taos数据库使用过程中突发“unable to establish connection”问题解决
项目使用的版本信息 1.taos的版本信息 3.0.4.1 2.jdbc的版本 3.2.1 3.druid连接池版本 1.2.11问题描述 Java应用服务连接,突然大量抛出如下的异常信息导致应用宕机: sql: select server_status(), desc: unable to establish connection和集团DBA沟通…...

【Qt】Qt中将字符串转换为数字类型的函数总结以及用法示例
在Qt中,可以使用以下函数将字符串转换为数字类型: toInt():将字符串转换为int类型。toDouble():将字符串转换为double类型。toFloat():将字符串转换为float类型。toLongLong():将字符串转换为long long类型…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
