二叉树顺序结构及实现
👉二叉树顺序结构及实现
- 1.二叉树的顺序结构
- 2.堆的概念及结构
- 3.堆的实现
- 3.1堆向下调整算法
- 3.2堆向上调整算法
- 4.堆的创建
- 4.1堆创建方法1
- 4.1.1构建堆结构体
- 4.1.2堆的初始化
- 4.1.3堆数据添加+向上调整
- 4.1.4主函数内容
- 4.2堆的创建方法2
- 4.2.1堆数据添加+向下调整
- 4.3堆数据的删除
- 4.4取根节点的数据
- 4.5回收内存
- 4.6Heap.h头文件展示
- 4. 6Heap.c源文件展示
- 4.7text.c源文件展示
- 5.堆的用途
- 5.1堆排序
- 5.2 TopK问题

所属专栏:初始数据结构❤️
🚀 >博主首页:初阳785❤️
🚀 >代码托管:chuyang785❤️
🚀 >感谢大家的支持,您的点赞和关注是对我最大的支持!!!❤️
🚀 >博主也会更加的努力,创作出更优质的博文!!❤️
🚀 >关注我,关注我,关注我,重要的事情说三遍!!!!!!!!❤️
1.二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而
完全二叉树更适合使用顺序结
构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段
- 简单点解释一下上面的意思就是,我们一般用
顺序结构来实现完全二叉树,而具体是实现方法就是我们把树中的节点都放到一个数组使其看起来是树的结构,但是存储方式是以数组的方式存储的。
我们用一张图片来清晰的理解一下。
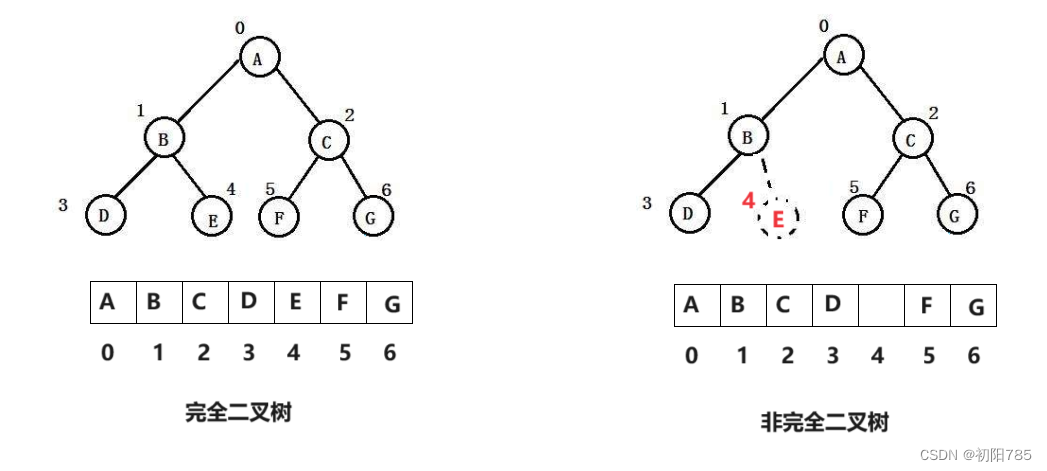
- 通过上面的两个图对比,只有完全二叉树才可以用顺序表存储,也只有这样才能体现出
顺序表的特点——(连续存储数据)
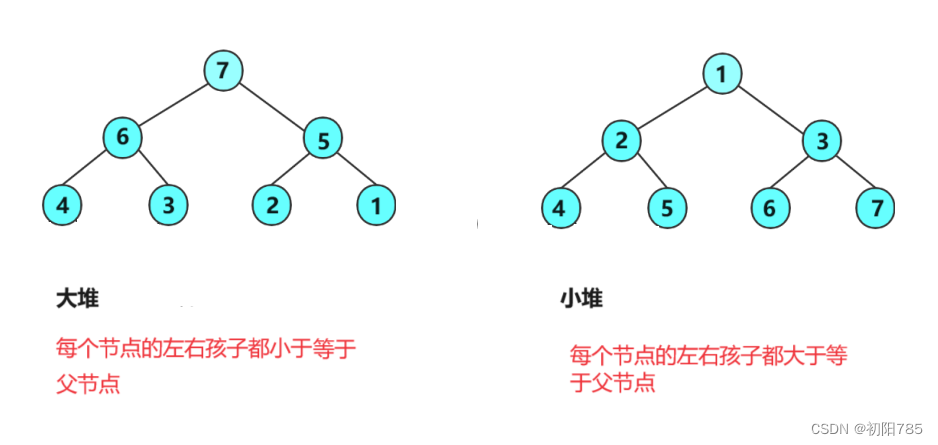
2.堆的概念及结构
说到堆大家可能立马会想起我们操作系统虚拟进程地址空间,但是这里我们要讲的是,我们二叉树的堆和操作系统虚拟进程地址空间中的堆是两回事,我们二叉树中的堆是一种数据结构。
如果有一个关键码的集合K = { k0,k1 ,k2 ,…,k(n-1) },把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中,并满足:Ki <=K(2 * i+1) 且 Ki <= K(2 * i + 2) 或者 (Ki >=K(2 * i+1) 且 Ki >= K(2 * i + 2)) i = 0,1,
2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆
堆的性质:
-
堆中某个节点的值总是不大于或不小于其父节点的值;
-
堆总是一棵完全二叉树
-
用一句话总结就是:
大堆就是一颗完全二叉树中的每一个节点的左右孩子都小于等于父节点。
小堆就是一颗完全二叉树中的每一个节点的左右孩子都大于等于父节点。
3.堆的实现
3.1堆向下调整算法
- 现在我们给出一个数组,
逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整
成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
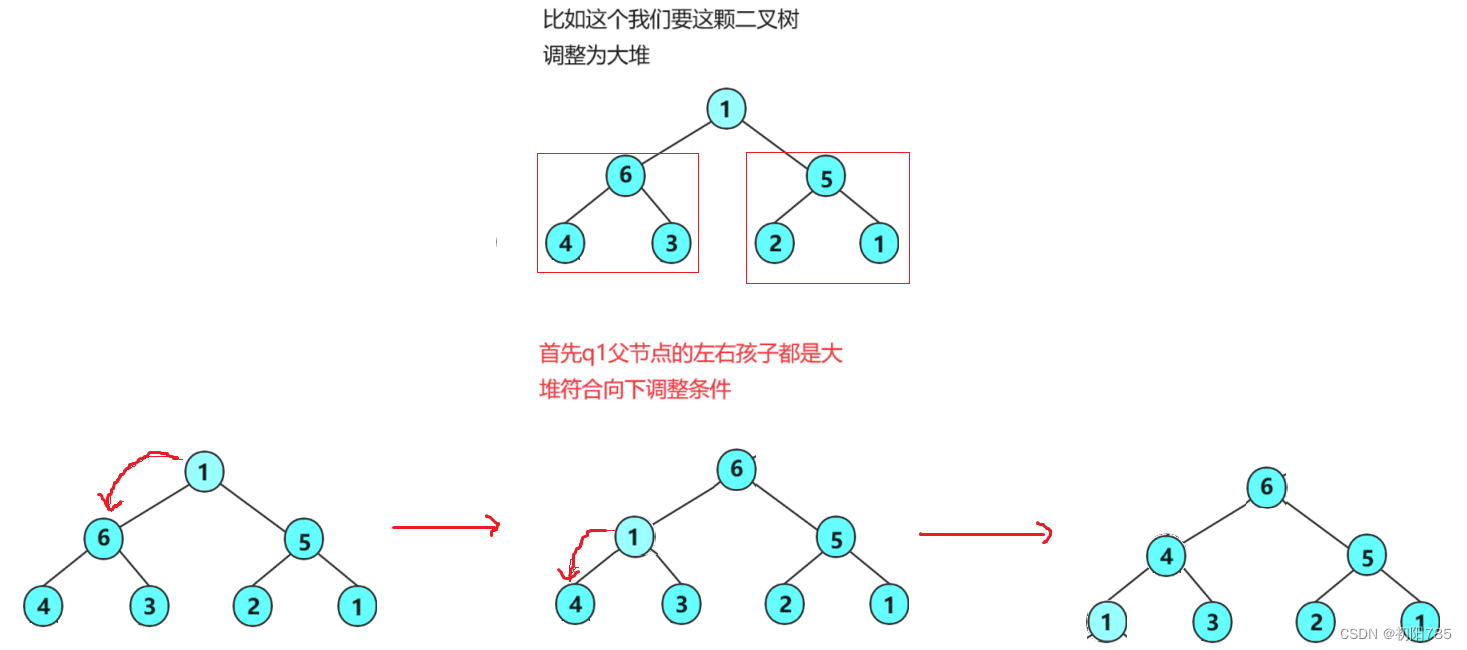
int arr[ ] = {1, 6, 5, 4, 3, 2 , 1} —— 调整前
int arr[ ] = {6, 4, 5, 1, 3, 2 , 1} ——调整后
3.2堆向上调整算法
- 我们堆的向上调整也是需要
左右节点是堆
4.堆的创建
4.1堆创建方法1
4.1.1构建堆结构体
- 我们现在实现树的方式是顺序表,结合我们之前学习的顺序表,我们可以很快的想到我们要创建一个结构体,结构体包含了
arr数组指针用来存放树的数据,size用来记录树节点当前的个数,capacity用来记录树的容量。
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
4.1.2堆的初始化
- 初始化就比较简单,刚开始我们的树就是为空的。
void HeapInit(HP* php)
{assert(php);php->size = php->capacity = 0;php->a = NULL;
}
4.1.3堆数据添加+向上调整
- 我们实现堆的方式是顺序表,也就是说我们需要一个数组来存放树,所以我们就把数组当作是一颗树来进行。
那么既然数组中存放着数据,那我们要怎么把一个乱序的数组给调整为一个堆呢?🤔这里我们先使用向上调整算法。
于是我们就想到了,我们就把数组中的数据一个一个的放到树中,每当放一个进去的时候我们都进向上调整一下,这样我们每次进行向调整的时候都满足向上调整的要求(左右孩子是堆)。
void HeapPush(HP* php, HPDataType x)
{assert(php);//检查容量,和顺序表那章节是一样的这里就不多展开讲解了if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? php->capacity = 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}else{php->a = tmp;php->capacity = newCapacity;}}//把数据放到树中php->a[php->size] = x;php->size++;//向上调整AdjustHeapUp(php->a, php->size - 1);
}
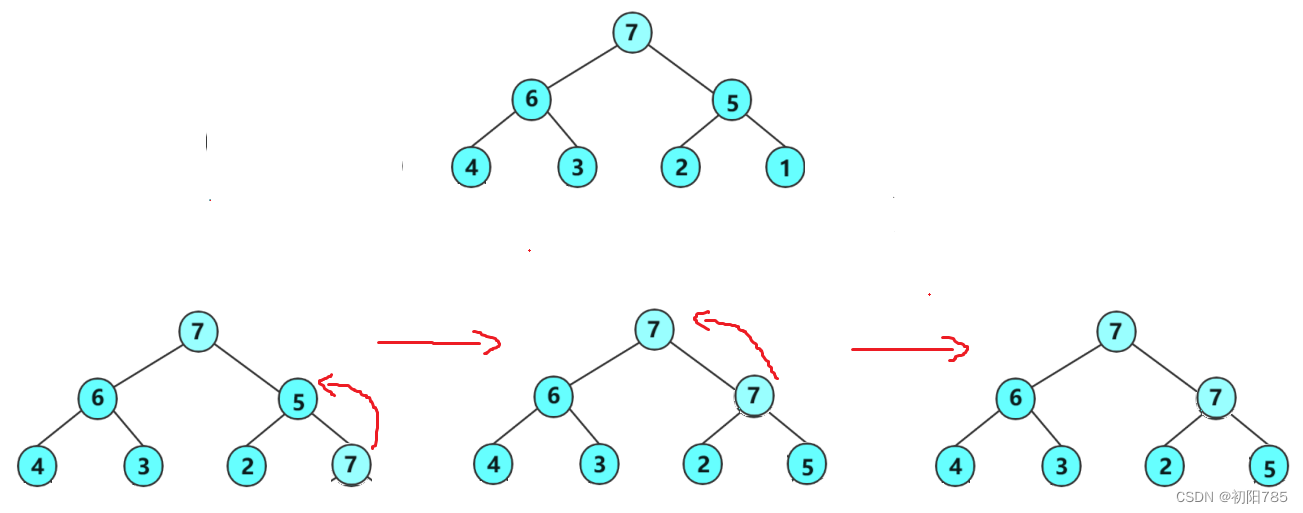
- 而我们知道向上调整的条件是左右孩子是堆,这里我们
以建大堆为例。只要我们的child大于我们的faster我么就向上调整,也就是child和faster进行交换,以此类推更新child和faster。
void Swap(int* a, int* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}void AdjustHeapUp(HPDataType* a, int child)
{//怎么通过child求parent我们上一章节也见过了不明白的小伙伴可以再去看一看int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}//如果不符合我们直接跳出,因为如果不符合了就一定是形成了大堆,因为向上调整的条件就是左右孩子都是堆。else{break;}}
}
我们来画张图进行深入的剖析。
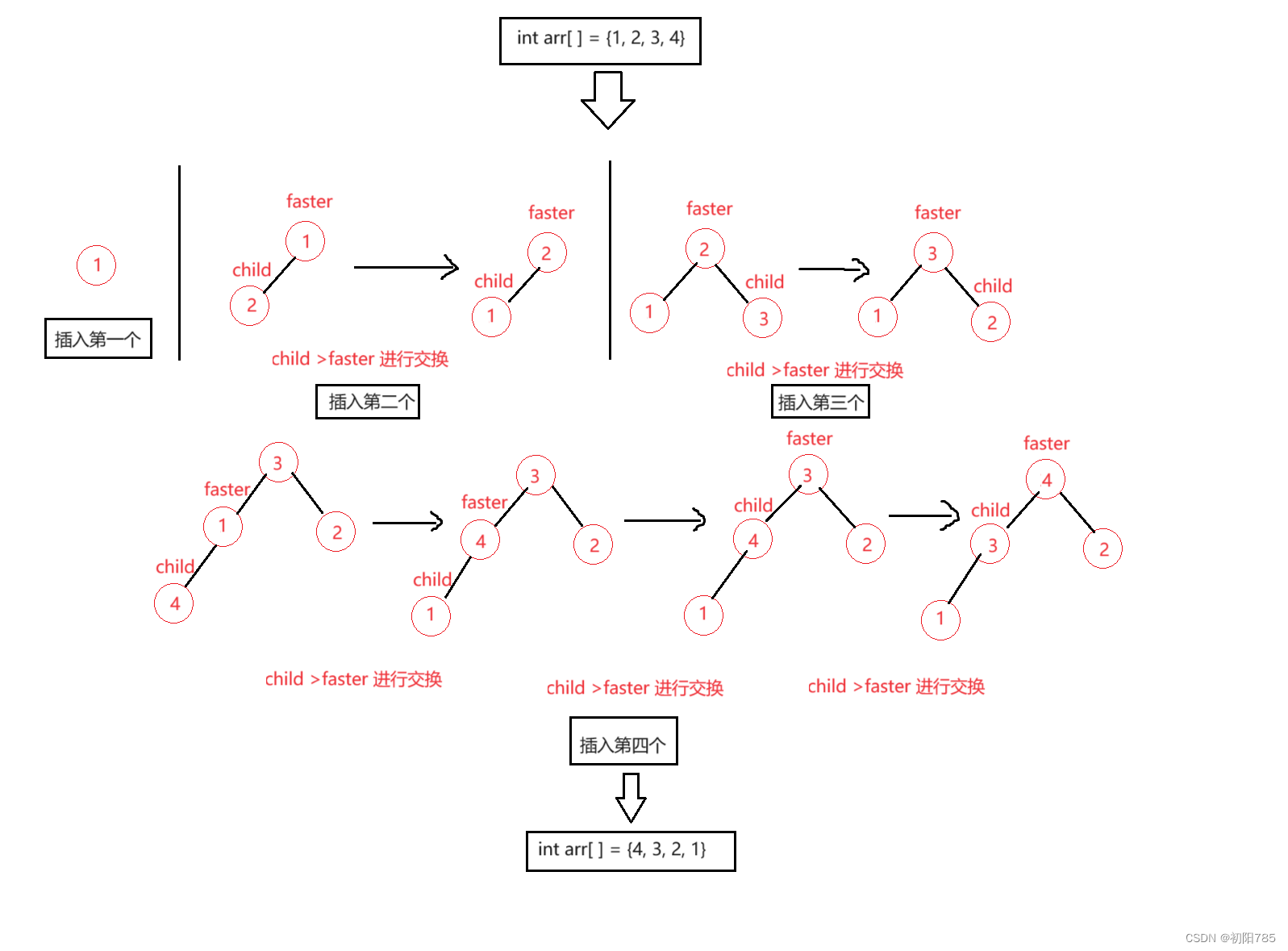
- 其实上面的方法可以在优化一下,既然是通过一个一个的插入再向上调整的话,也就是说是按照数组的下标一次的向上调整,那我们不如
一步到位直接将数组中的数据memcpy到树中,然后从通过一个for循环按照下标 的方式向上调整。
void HeapInitArr(HP* php, int* a, int n)
{assert(php);HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * n);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;memcpy(php->a, a, sizeof(HPDataType) * n);php->size = n;php->capacity = n;for (int i = 1; i < n; i++ ){AdjustHeapUp(php->a, i);}
}
4.1.4主函数内容
int main()
{int a[] = { 56,89,2,33,6,2,55,6,9,33,8 };HP hp;HeapInit(&hp);//建造堆for (int i = 0; i < sizeof(a)/sizeof(HPDataType); i++){HeapPush(&hp, a[i]);//通过一个一个插入再向上调整建堆}HeapPrint(&hp);HeapDestry(&hp);return 0;
}
4.2堆的创建方法2
4.2.1堆数据添加+向下调整
-
看到这里的小伙伴有没有发现,我们在建堆的时候,不仅在
栈上开辟了一个数组用来存放要插入树中的数据,还在堆区开辟了一块内存表示树,但是有没有发现其实这两个地方本质上都是数组,那为什么还要开辟堆上的内存呢?直接在数组上进行不就行了?于是我们就有了向下调整。 -
我们建堆除了用向上调整还
可以用向下调整,假想一下我们用向上调整的方法用到向下调整上会是怎么样的。也就是说我们每插入一个数据就向下调整,但是这显然是行不通的,因为插入一个数据后,后面根本就没有数据了,何来的向下调整。于是我们不能和向上调整一样一个一个数据的插入,而是直接在数组上进行调整。那么问题也来了,向下调整也是要求左右孩子是堆才能进行的,如果我们从根节点开始的话就不满足条件了,所以我们从最后一个节点的度不为0的节点开始向上调整就行了,而当我我们调整好了当前节点之后需要调整下一个节点的时候只需要当前节点减减就可以找到另一个需要调整的节点就行了。
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void AdjustDown(HPDataType* a, int n, int parent)
{assert(a);//先假设左左孩子int child = parent * 2 + 1;while (child < n){//判断是右孩子小还是左孩子小//注意有可能不是满二叉树,可能只有左孩子没有右孩子,所以要判断child + 1 < n;if (child + 1 < n && a[child + 1] > a[child]){++child;}//判断parent是否小于孩子if (a[parent] < a[child]){Swap(&a[parent], &a[child]);//更新parentparent = child;child = parent * 2 + 1;}else{break;}}
}int main()
{int a[] = { 56,89,2,33,6,2,55,6,9,33,8 };HP hp;int len = sizeof(a) / sizeof(int);//解释一下(len-2)/ 2: len是数组的长度,但是我们操作的是下标所以说是len - 1,//而我们最后一个度不为0的节点的孩子节点肯定是包含了最后一个叶子节点,所以显然可以求出最后一个度不为0 的节点就是(len - 1 - 1) / 2for (int i = (len - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, len - 1, i);}for (int i = 0; i < len; i++){printf("%d ", a[i]);}return 0;
}
- 如果这里你看明白了,相信你也发现了,我们的向上调整也是可以这样做的,这里就留给小伙伴们自行思考了,如果有任何问题都可以在在评论区中提问的哦。
4.3堆数据的删除
⚠️⚠️注:这里我们还是使用第一种建堆的方法。
- 既然我们建好了堆,我们要删除堆的数据,如果说只是
删除堆的最后一个数据那就显得很没有意义,所以我们删除堆的数据是删除根节点的数据。设想一下,如果我们直接删除根节点的树后,因为我们是使用顺序表存放树的数据的,直接暴力删除根节点就会破坏我们原先建好的堆结构,如果我们还要有堆的结构的话我们就对再次通过建堆的方式重新建堆这无疑是一件大工程。那么有什么好的方法可以做到既删除数据,还可以保留堆的结构呢?于是我们就想到了可以讲根节点与最后一个叶子节点进行交换,然后再删除尾,再做一次向下调整就行了。
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size - 1, 0);
}
4.4取根节点的数据
HPDataType HeapTop(HP* php)
{assert(php);return php->a[0];
}
4.5回收内存
这个讲了很多遍了,这里就简单略过。
void HeapDestry(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
4.6Heap.h头文件展示
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
void AdjustDown(HPDataType* a, int n, int parent);
void AdjustHeapUp(HPDataType* a, int child);
void Swap(int* a, int* b);void HeapPrint(HP* php);
void HeapInit(HP* php);
void HeapInitArr(HP* php, int * a, int n);
void HeapDestry(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
4. 6Heap.c源文件展示
#define _CRT_SECURE_NO_WARNINGS 1
#include "deap.h"void HeapInit(HP* php)
{assert(php);php->size = php->capacity = 0;php->a = NULL;
}void HeapInitArr(HP* php, int* a, int n)
{assert(php);HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * n);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;memcpy(php->a, a, sizeof(HPDataType) * n);php->size = n;php->capacity = n;for (int i = 1; i < n; i++ ){AdjustHeapUp(php->a, i);}
}void HeapDestry(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
void Swap(int* a, int* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}void AdjustHeapUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);//检查容量if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? php->capacity = 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}else{php->a = tmp;php->capacity = newCapacity;}}php->a[php->size] = x;php->size++;//向上调整AdjustHeapUp(php->a, php->size - 1);
}void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}
}void AdjustDown(HPDataType* a, int n, int parent)
{assert(a);//先假设左左孩子int child = parent * 2 + 1;while (child < n){//判断是右孩子小还是左孩子小//注意有可能不是满二叉树,可能只有左孩子没有右孩子,所以要判断child + 1 < n;if (child + 1 < n && a[child + 1] > a[child]){++child;}//判断parent是否小于孩子if (a[parent] < a[child]){Swap(&a[parent], &a[child]);//更新parentparent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size - 1, 0);
}HPDataType HeapTop(HP* php)
{assert(php);return php->a[0];
}4.7text.c源文件展示
int main()
{int a[] = { 56,89,2,33,6,2,55,6,9,33,8 };HP hp;HeapInit(&hp);//建造堆for (int i = 0; i < sizeof(a)/sizeof(HPDataType); i++){HeapPush(&hp, a[i]);}HeapPrint(&hp);printf("\n");//这样就可以打印出一个排完序的数据while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}HeapDestry(&hp);return 0;
}
5.堆的用途
5.1堆排序
- 堆的用途之一就是进行
堆排序,那么如果我们得到一个升序的数组的话我我们应该建大堆还是小堆呢?🤔我相信大部分人的第一反应就是建小堆,为什么呢,因为如果是小堆的话,我们就可以找到堆中最小的那个数据,然后通过在创建一个数组的方式以及堆Top的方法把最小的放到新建的数组中,固然这是一个方法,但是不是一个好方法,我们能不能就再原数组中进行排序呢?🤔答案是可以的,这时我们建的是大堆。我们的思路是建好一个大堆后,把最后一个叶子节点和根节点进行交换交换后我们的树的节点个数减1,然后进行向下调整,这个时候我们的数组中最大的数到了最后一个并且向下调整的时候不参与调整,以此类推知道数的节点个数为0为止我们就排好序了。
void sort(int* a, int n)
{//把数组直接看成是一个对,然后对其进行向上调整,得到大堆//升序建大堆,降序建小堆int i = 0;for (int i = 1; i < n; i++){AdjustHeapUp(a, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//向下调整AdjustDown(a, end, 0);end--;}
}int main()
{int a[] = { 56,89,2,33,6,2,55,6,9,33,8 };sort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}
}

相反的如果要弄降序就建小堆。
5.2 TopK问题
-
所谓TopK就是取出前K个最大的数,或者后K个最小的数。
这里就那取出前K个最大的数来举例子,而且是以文件的形式进行存储。 -
假如有n个数据,找出前k个最大的数据。
-
我们的方法就是:
1️⃣ .先创建一个节点个数为K的小堆
2️⃣ .一次遍历n-k个数据
3️⃣ .每次遍历后都与根节点比较,如果大于根节点就是根节点等于该数据,再进行向下调整
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>//HeapTopK问题,找出数据中前k个大的数据
//步骤:
// 1.先创建k个节点的堆(如果是找前k的大的数据就建小堆,如果是找前k个小的就建大堆)
// 2.然后用剩下的数据和堆的根比较,如果比根大就替换,然后向下调整
// 3.遍历完毕后堆中的数据就是想要的结果了。const int N = 10000;void CreatData()
{//设置随机种子srand((unsigned int)time(NULL));const char* file_name = "data.txt";//将数据写到文件中FILE* file = fopen(file_name, "w");if (file == NULL){perror("fopen file");return;}for (int i = 0; i < N; i++){int x = rand() % 1000000;fprintf(file, "%d\n", x);}fclose(file);
}void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void AdjustDown(int* a, int k ,int parent)
{int child = parent * 2 + 1;while (child < k){if (child + 1 < k && a[child + 1] < a[child]){child++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}void print_topK(int k)
{int arr1[10000];//首先把文件中的前k个数据放到堆中,创建小堆FILE* file = fopen("data.txt", "r");//创建存放堆的顺序表int* arr2 = (int*)malloc(sizeof(int) * k);if (arr2 == NULL){perror("malloc");return;}for (int i = 0; i < N; i++){int x = 0;fscanf(file, "%d", &x);arr1[i] = x;}//把前k个数据放到arr中for (int i = 0; i < k; i++){arr2[i] = arr1[i];}//向下调整,形成小堆for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(arr2,k, i);}//遍历剩下的数据for (int i = k; i < N; i++){if (arr2[0] < arr1[i]){arr2[0] = arr1[i];AdjustDown(arr2, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", arr2[i]);}fclose(file);
}int main()
{int k = 10;//创建10000个数据放到文件中//CreatData();print_topK(10);
}
相关文章:

二叉树顺序结构及实现
👉二叉树顺序结构及实现 1.二叉树的顺序结构2.堆的概念及结构3.堆的实现3.1堆向下调整算法3.2堆向上调整算法 4.堆的创建4.1堆创建方法14.1.1构建堆结构体4.1.2堆的初始化4.1.3堆数据添加向上调整4.1.4主函数内容 4.2堆的创建方法24.2.1堆数据添加向下调整 4.3堆数据…...

python读取influxdb中数据
示例代码一:从infludb中获取指定时间段time和value值,并作图保存 from influxdb_client import InfluxDBClient import matplotlib.pyplot as plt# InfluxDB连接信息 url "http://localhost:8086" token "your_token" org "…...
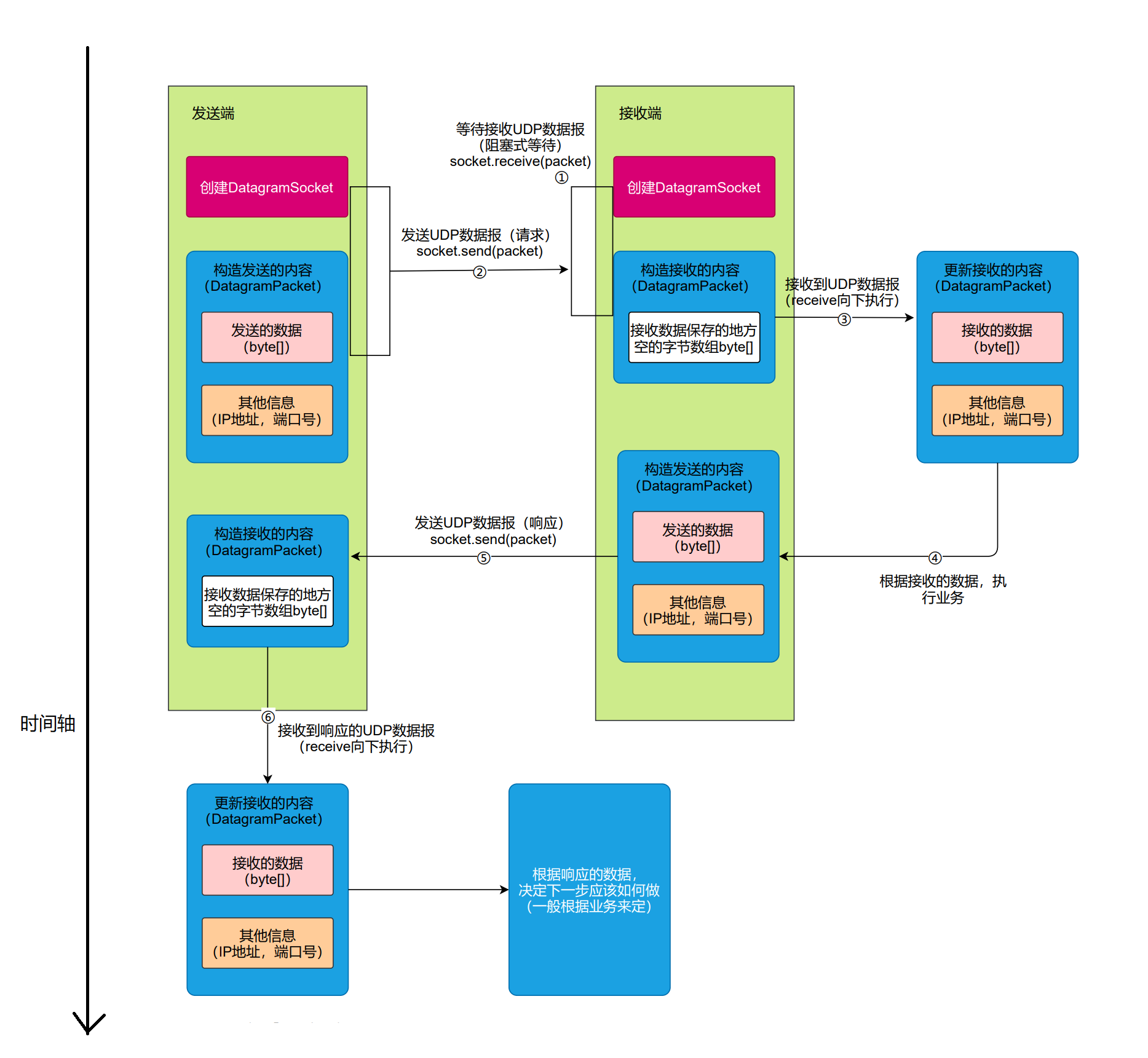
【网络编程】UDP Socket编程
UDP Socket编程 一. DatagramSocket二. DatagramPacket三. InetSocketAddress四. 执行流程五. 代码示例: UDP 回显服务器 数据报套接字: 使用传输层 UDP 协议 UDP: 即 User Datagram Protocol(用户数据报协议),传输层协议。 UDP…...

[GIT]版本控制工具
[GIT]版本控制工具 Git 的命令Git 的配置信息查看现有 Git 配置信息设置 Git 配置信息用户信息配置文本编辑器配置差异分析工具配置 编辑 Git 配置文件 Git 仓库操作初始化 Git 仓库克隆 Git 仓库Git 分支仓库创建Git 远程仓库命令 Git 提交历史Git 标签添加标签查看已有标签删…...

Linux文件管理命令
Linux命令行 命令空格参数(可写可不写)空格文件(可写可不写)ls/opt 根目录下的opt文件夹ls-a 显示所有文件及隐藏文件/optls -l 详细输出文件夹内容 ls -h 输出文件大小(MB...)ls--full-time 完整时间格式输出ls-d 显示文件夹本身信息,不输出内容ls-t 根据最后修改…...
)
Netty面试题(三)
文章目录 前言一、如何选择序列化协议?二、Netty 的零拷贝实现?总结 前言 如何选择序列化协议?Netty 的零拷贝实现? 一、如何选择序列化协议? 具体场景 对于公司间的系统调用,如果性能要求在 100ms 以上的…...
risc-v dv源代码分析
地址为 GitHub - chipsalliance/riscv-dv: Random instruction generator for RISC-V processor verificationRandom instruction generator for RISC-V processor verification - GitHub - chipsalliance/riscv-dv: Random instruction generator for RISC-V processor verif…...

C语言基础语法复习07-c语言关键字的解释
对前一篇文章写点随笔:https://blog.csdn.net/weixin_43172531/article/details/132893176 基本数据类型(8种)和类型修饰符(4种): void与指针*组合在一起才有具体实体意义。 void本身代表没有类型、没有实体,例如void main(void)。 char c…...
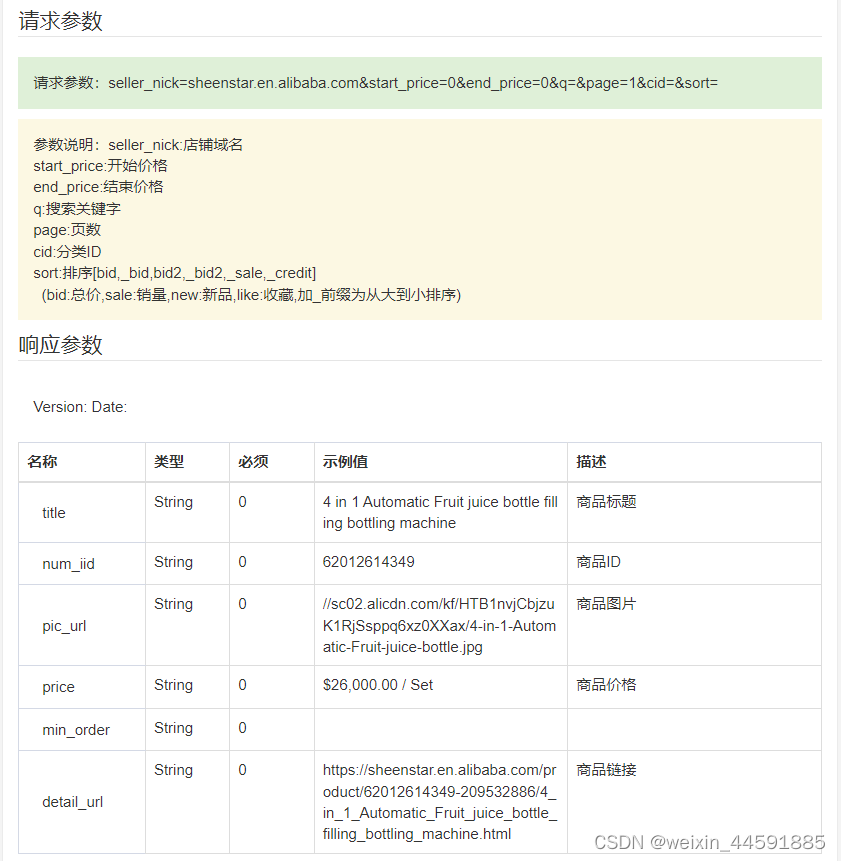
阿里巴巴全店商品采集教程,阿里巴巴店铺所有商品接口(详解阿里巴巴店铺所有商品数据采集步骤方法和代码示例)
随着电商行业的快速发展,阿里巴巴已成为国内的电商平台之一,拥有着海量的商品资源。对于一些需要大量商品数据的商家或者需求方来说,阿里巴巴全店采集是非常必要的。本文将详细介绍阿里巴巴全店采集的步骤和技巧,帮助大家更好地完…...

Android 白天黑夜模式设置
白天黑夜模式是一种动态的UI模式,根据当前时间或用户设置的偏好,在白天和黑夜之间进行切换。它通过调整应用程序的颜色、亮度和其他可视化元素来提供更加舒适和易读的用户界面。 一、简单设置 UiModeManager 是用于管理和控制用户界面模式(UI Mode)。它提供了一组方法,允…...

FFMpeg zoompan 镜头聚焦和移动走位
案例 原始图片 # 输出帧数,默认25帧/秒,25*4 代表4秒 # s1280x80 # 输出视频比例,可以设置和输入图片大小一致 # zoom0.002 表示每帧放大的倍数,下面代码是25帧/每秒 * 4秒,共1000帧 # 最终是 0.002*25*4 0.2&…...
利用hutool工具类实现验证码功能
hutool工具类实现验证码 一.生成验证码二.校验验证码三.使用案例1.引入hutool工具类2.VerifyCodeResp接口响应体3.VerifyCodeController验证码工具类4.测试验证5.项目结构及源码下载 利用hutool工具类,可以很方便生成不同类型的验证码。这里简单记录下使用过程。 一…...

前端面试题: 请解释什么是函数的作用域?
今天做到了一道题:请解释什么是函数的作用域? 我给的答案是: 函数的作用域是指函数执行到内部后创建的数据空间,在函数的作用域内,let定义的变量的有效期为函数作用域 AI觉得我答得比较简单:回答基本正确&…...

华为云云服务器云耀L实例评测 | 华为云云服务器实例新品全面解析
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Nginx配置SSL证书
1 Ubuntu 20.04 上安装 Nginx Nginx 发音 “engine x” ,是一个开源软件,高性能 HTTP 和反向代理服务器,用来在互联网上处理一些大型网站。它可以被用作独立网站服务器,负载均衡,内容缓存和针对 HTTP 和非 HTTP 的反向代理服务器。…...

一,安卓aosp源码编译环境搭建
系列文章目录 第一章 安卓aosp源码编译环境搭建 第二章 手机硬件参数介绍和校验算法 第三章 修改安卓aosp代码更改硬件参数 第四章 编译定制rom并刷机实现硬改(一) 第五章 编译定制rom并刷机实现硬改(二) 第六章 不root不magisk不xposed lsposed frida原生修改定位 第七章 安卓…...
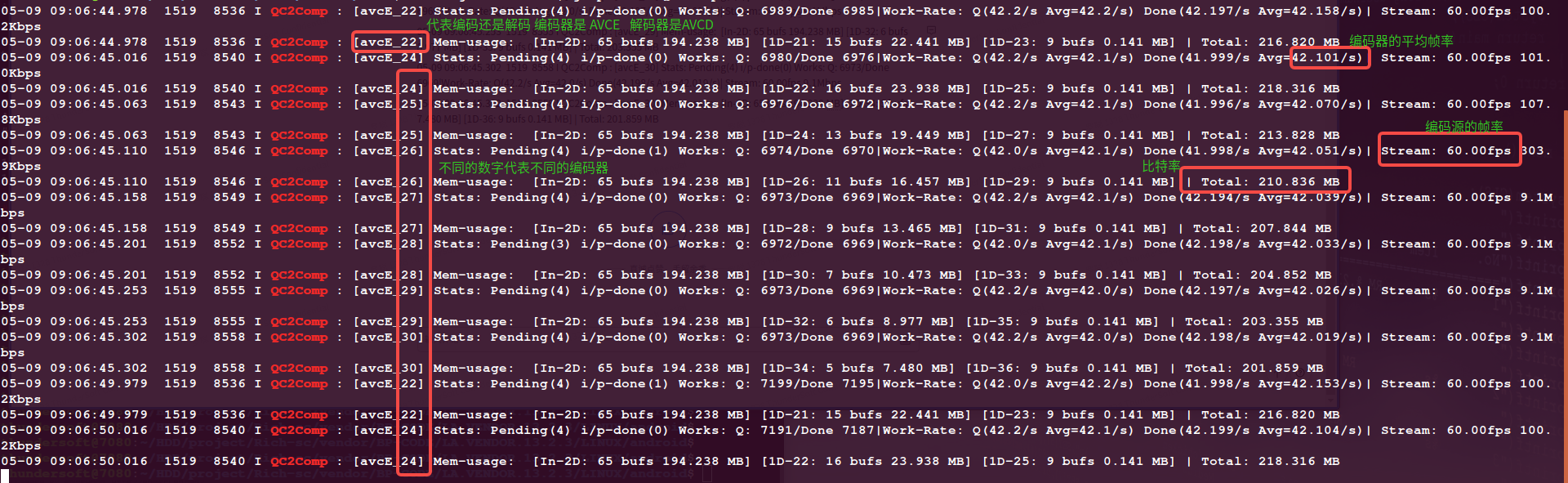
video 视频编解码一些debug方法
文章目录 一、通过命令去获取一些数据1.2 确定我们xml配置文件: 二、查看我们芯片支持的编码能力三、通过log去获取信息 这个文章的主要内容是为了后期性能方面的debug, 设计到前期的bringup则没有 一、通过命令去获取一些数据 获取媒体相关的参数: # getprop |…...

中秋国庆假期——模板推荐
要说最近能让人开心的事情是什么?大概就是下周将迎来8天假,小编帮大家数了数还有11天,就要放中秋国庆的假期了。作为一个资深打工人,本周的日常即将变成:上班想放假、下班想放假、想放假… 但是宝子们要注意,大家在盼…...

【配代码演示】Cookie和Session的区别
一、共同之处: cookie和session都是用来跟踪浏览器用户身份的会话方式。 二、工作原理: 1.Cookie的工作原理 (1)浏览器端第一次发送请求到服务器端 (2)服务器端创建Cookie,该Cookie中包含用户的…...
【Linux初阶】信号入门2 | 信号阻塞、捕捉、保存
文章目录 ☀️前言☀️一、信号阻塞🌻1.信号其他相关常见概念🌻2.信号在内核中的表示 ☀️二、信号捕捉(重点)🌻1.用户态 & 内核态🌻2.如何判断进程处于用户态或内核态🌻3.OS接口的访问方法…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
