【考研数学】高等数学第六模块 —— 空间解析几何(1,向量基本概念与运算)
文章目录
- 引言
- 一、空间解析几何的理论
- 1.1 基本概念
- 1.2 向量的运算
- 写在最后
引言
我自认空间想象能力较差,所以当初学这个很吃力。希望现在再接触,能好点。
一、空间解析几何的理论
1.1 基本概念
1.向量 —— 既有大小,又有方向的量称为向量,常用从起点指向终点的带箭头的有向线段 A B → \overrightarrow{AB} AB 表示,或用带箭头的小写字母 a → \overrightarrow{a} a 。
向量的大小或长度称为向量的模,向量 a → \overrightarrow{a} a 的模记作 ∣ a → ∣ |\overrightarrow{a}| ∣a∣ 。特别地,模为 1 的向量称为单位向量,模为 0 的向量称为零向量,记作 a → 0 \overrightarrow{a}^0 a0 。大小相等且方向相同的向量相等。
2.向量的坐标 —— 设 i → , j → , k → \overrightarrow{i},\overrightarrow{j},\overrightarrow{k} i,j,k 分别表示 x , y , z x,y,z x,y,z 轴正向的单位向量,设向量 a → \overrightarrow{a} a 在三个坐标轴上的投影分别为 a , b , c a,b,c a,b,c ,由向量的分解得 a → = a i → + b j → + c k → = { a , b , c } \overrightarrow{a}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}=\{a,b,c\} a=ai+bj+ck={a,b,c} ,称 { a , b , c } \{a,b,c\} {a,b,c} 为向量 a → \overrightarrow{a} a 的坐标。
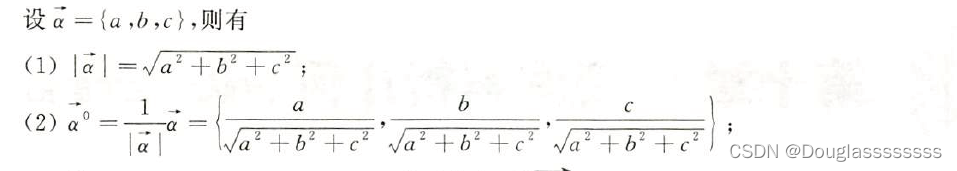
3.向量的方向角和方向余弦 —— 设 a → = { a , b , c } \overrightarrow{a}=\{a,b,c\} a={a,b,c} 为非零向量,则 a → \overrightarrow{a} a 与 x , y , z x,y,z x,y,z 轴正向的夹角,称为此向量的方向角,分别记为 α , β , γ \alpha,\beta,\gamma α,β,γ ,称 cos α , cos β , cos γ \cos\alpha,\cos\beta,\cos\gamma cosα,cosβ,cosγ 为 a → \overrightarrow{a} a 的方向余弦。则 cos α = a a 2 + b 2 + c 2 , cos β = b a 2 + b 2 + c 2 , cos α = c a 2 + b 2 + c 2 \cos\alpha=\frac{a}{\sqrt{a^2+b^2+c^2}},\cos\beta=\frac{b}{\sqrt{a^2+b^2+c^2}},\cos\alpha=\frac{c}{\sqrt{a^2+b^2+c^2}} cosα=a2+b2+c2a,cosβ=a2+b2+c2b,cosα=a2+b2+c2c 显然,有 a → 0 = { cos α , cos β , cos γ } \overrightarrow{a}^0=\{\cos\alpha,\cos\beta,\cos\gamma\} a0={cosα,cosβ,cosγ} , cos α 2 + cos β 2 + cos γ 2 = 1 \cos\alpha^2+\cos\beta^2+\cos\gamma^2=1 cosα2+cosβ2+cosγ2=1 。
4.向量在一个轴(向量)上的投影 —— 设 u u u 为一个数轴, a → \overrightarrow{a} a 为一个向量,过向量的起点 A 和终点 B 作 u u u 轴的垂直面交 u u u 轴于点 A 1 , B 1 A_1,B_1 A1,B1 ,其在 u u u 轴上的坐标分别为 x 1 , x 2 x_1,x_2 x1,x2 ,称 x 2 − x 1 x_2-x_1 x2−x1 为向量 a → \overrightarrow{a} a 在 u u u 轴上的投影,记为 P r j u a → = x 2 − x 1 Prj_u\overrightarrow{a}=x_2-x_1 Prjua=x2−x1 ,且 P r j u a → = ∣ a → ∣ cos ( u , a → ) Prj_u\overrightarrow{a}=|\overrightarrow{a}|\cos(u,\overrightarrow{a}) Prjua=∣a∣cos(u,a) 。
1.2 向量的运算
(一)几何描述
加减法,遵循三角形法则。



(二)代数描述
主要说一下叉乘(向量积)的代数形式:

下面是一些运算的性质:

写在最后
有关向量的基本概念和性质基本就这些,下一篇我们就来看看向量有哪些应用。
相关文章:

【考研数学】高等数学第六模块 —— 空间解析几何(1,向量基本概念与运算)
文章目录 引言一、空间解析几何的理论1.1 基本概念1.2 向量的运算 写在最后 引言 我自认空间想象能力较差,所以当初学这个很吃力。希望现在再接触,能好点。 一、空间解析几何的理论 1.1 基本概念 1.向量 —— 既有大小,又有方向的量称为向…...

巨人互动|Facebook海外户Facebook客户反馈分数
Facebook客户反馈分数是一项用于衡量用户对Facebook产品和服务满意度的指标。该指标被广泛应用于各种调研和评估活动,帮助Facebook了解用户对其平台和功能的意见和建议,并从中识别出改进的机会。 巨人互动|Facebook海外户&Facebook新闻提要的算法&am…...
Tomcat多实例部署和动静分离
一、多实例部署: 多实例:多实例就是在一台服务器上同时开启多个不同的服务端口,同时运行多个服务进程,这些服务进程通过不同的socket监听不同的服务端口来提供服务。 1.前期准备: 1.关闭防火墙:systemctl …...

关于 C/C++ 中在指针前加 const 关键字的作用说明
1. 作用说明: 在指针前加 const 的用途为:不可改变指针指向的内存的值,即将该指向指向的内存中的变量置为只读(read-only) 变量。 但是,可以给 const 的指针赋值,即将具有 const 属性的指针指向别的内存地…...
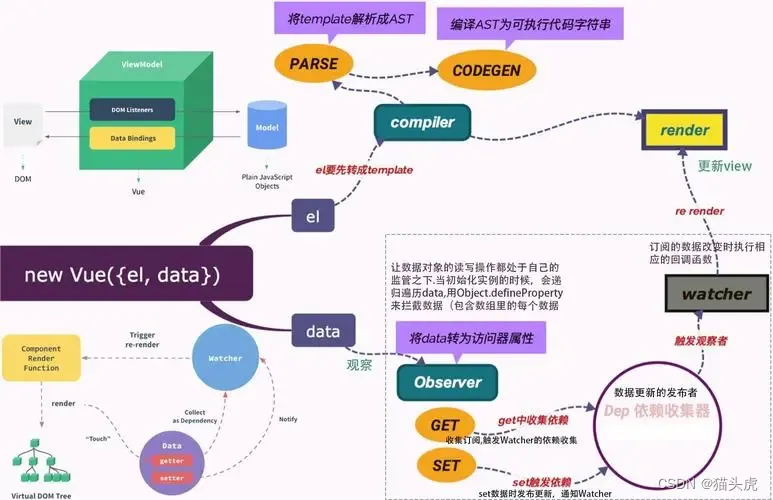
Vue.js新手指南:从零开始建立你的第一个应用
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【案例】--EasyExcel导入导出文件案例
目录 一、前言二、EasyExcel解析(导入)文件2.1、EasyExcel选型2.2、如何存储excel解析的文件2.3、解析格式规则的excel文件2.4、解析未知格式规则的excel文件三、EasyExcel解析(导出)文件3.1、导出基本代码实现一、前言 最近项目中,需要对excel、csv等文件进行解析,并做相关…...

深入探索图像处理:从基础到高级应用
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 图像处理是计算机视觉领…...
Jetpack Compose基础组件 - Image
Image的源码参数预览 Composable fun Image(painter: Painter,contentDescription: String?,modifier: Modifier Modifier,alignment: Alignment Alignment.Center,contentScale: ContentScale ContentScale.Fit,alpha: Float DefaultAlpha,colorFilter: ColorFilter? …...

UINavigationController内的页面跳转实现 UIViewController 的 present和dismiss动画
UINavigationController内部页面跳转默认为左右切换,但是当我们想向上弹出进入界面,或者向下离开界面时,需要实现UINavigationControllerDelegate 协议自行控制页面的动画(否则直接在navVc上叠加动画会导致动画结束后的那个页面,自…...
PMP对项目管理工作有什么用?
首先,项目管理岗位基本是不限行业的,所以,只要是项目管理相关的岗位,pmp证书都是能起到效果的,不用担心局限性太大,而且,pmp证书是国际证书,无论国企还是外企,都是认可这…...

Python 将‘20230919182550‘ 转换为 ‘%Y年%m月%d日 %H:%M‘
为了将给定的时间字符串 cur_time 转换为指定的格式,可以使用 Python 的 datetime 模块。以下是完成此操作的步骤: 使用 strptime 方法将 cur_time 转换为一个 datetime 对象。使用 strftime 方法将这个 datetime 对象转换为所需的格式。 这是具体的代…...

vue2.0检测无用的代码并删除
(1)、使用 useless-files-webpack-plugin 来查找无用文件 npm i useless-files-webpack-plugin -S (2)、vue.config.js中配置 const UselessFile require(useless-files-webpack-plugin)chainWebpack: config > {config.plu…...
小米华为,化干戈为玉帛!
近日来,手机圈又掀起了各大厂家推出新品的高潮。首先是华为Mate60的推出,其自研的麒麟9000S芯片瞬间点燃了国内手机市场,得到了国内甚至国外业界人士的认可和好评。 而近日网上盛传的小米创始人雷军的“愿意加入华为技术生态圈”的邀请&…...

【文末赠书】SRE求职必会 —— 可观测性平台可观测性工程(Observability Engineering)
文章目录 〇、导读一、实现可观测性平台的技术要点是什么?二、兼容全域信号量三、所谓全域信号量有哪些?四、统一采集和上传工具五、统一的存储后台六、自由探索和综合使用数据七、总结★推荐阅读《可观测性工程》直播预告直播主题直播时间预约直播 视频…...

content生成自定义图标的方式是什么?
animate.css是一个跨浏览器的CSS3动画库,它内置了很多经典的CSS3动画。使用起来很方便。下面我们通过例子讲解如何使用自定义类名和animate.css库实现动画效果。 (1)从animate.css官方网站获取animate.css文件,保存到chapter04目录中。 (2)创建C:\vue\…...

无涯教程-JavaScript - SECH函数
描述 SECH函数返回某个Angular的双曲正割。双曲正割是双曲余弦的倒数。因此,双曲正割的值由等式给出- $$\sinh\left(x\right)\frac {1} {\cosh\left(x\right)} \frac {2} {e ^ x e ^ {-x}} $$ 语法 SECH (number)争论 Argument描述Required/OptionalNumberNumber is the …...
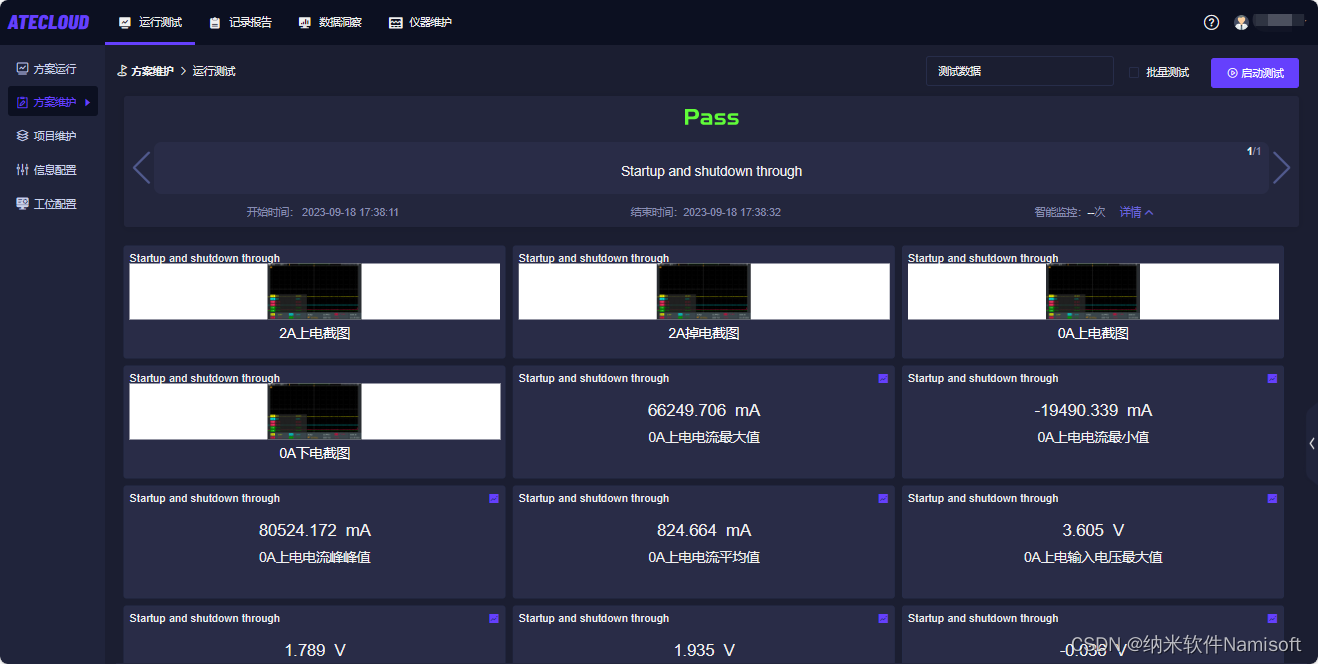
天宇微纳芯片ic测试软件如何测试芯片上下电功能?
芯片的上电与下电功能测试是集成电路生产和研发过程中的关键环节,可以帮助企业确保产品的可靠性、整合性和兼容性,同时提高生产效率和产品质量。 因此在芯片的研发设计中,企业会对芯片的上下电有严格的要求,包括上下电的时序&…...

1万多爱背句子英语口语ACCESS\EXCEL数据库
今天这个数据库包含3个表,一个是分类表,一个是分类章节有,一个是具体句子表,表与表之间可以根据相关ID进行关联,是一个学习英语的好数据,具体请查收截图或样本: 数据有ACCESS数据库文件…...

C++:new 和 delete
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》 文章目录 前言一、C内存管理1.内置类型2.自定义类型3.delete 与 new不匹配使用问题(VS平台下) 二、operator new 与 operator delete函数三、 new 和delete的实现原理内置类型自定义类型 四…...

mysql5.7版本的数据导入到mysql8.0版本需要怎么做
将 MySQL 5.7 版本的数据导入到 MySQL 8.0 版本,由于版本之间可能存在一些差异,需要采取一些步骤来确保数据导入的顺利进行。以下是一般的导入步骤: 备份数据: 在进行任何操作之前,务必备份 MySQL 5.7 数据库。可以使用…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
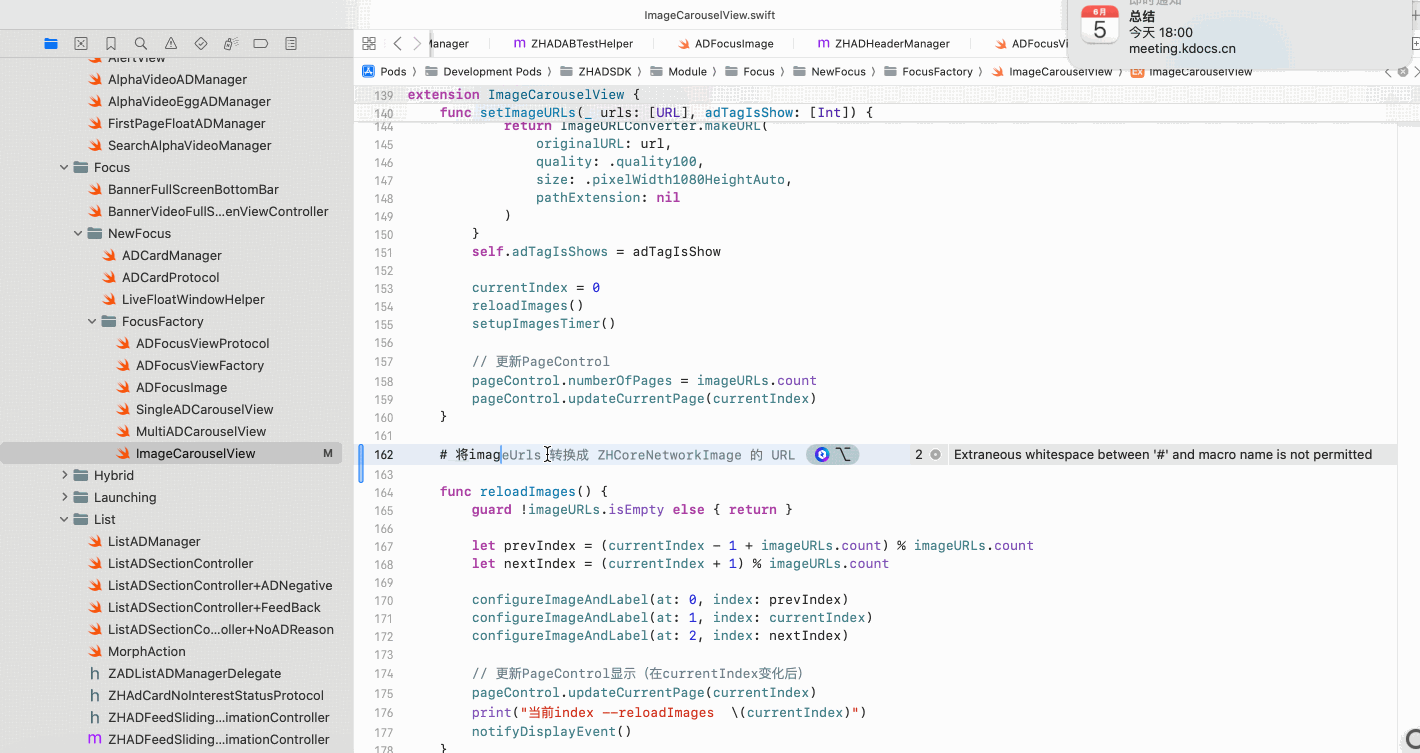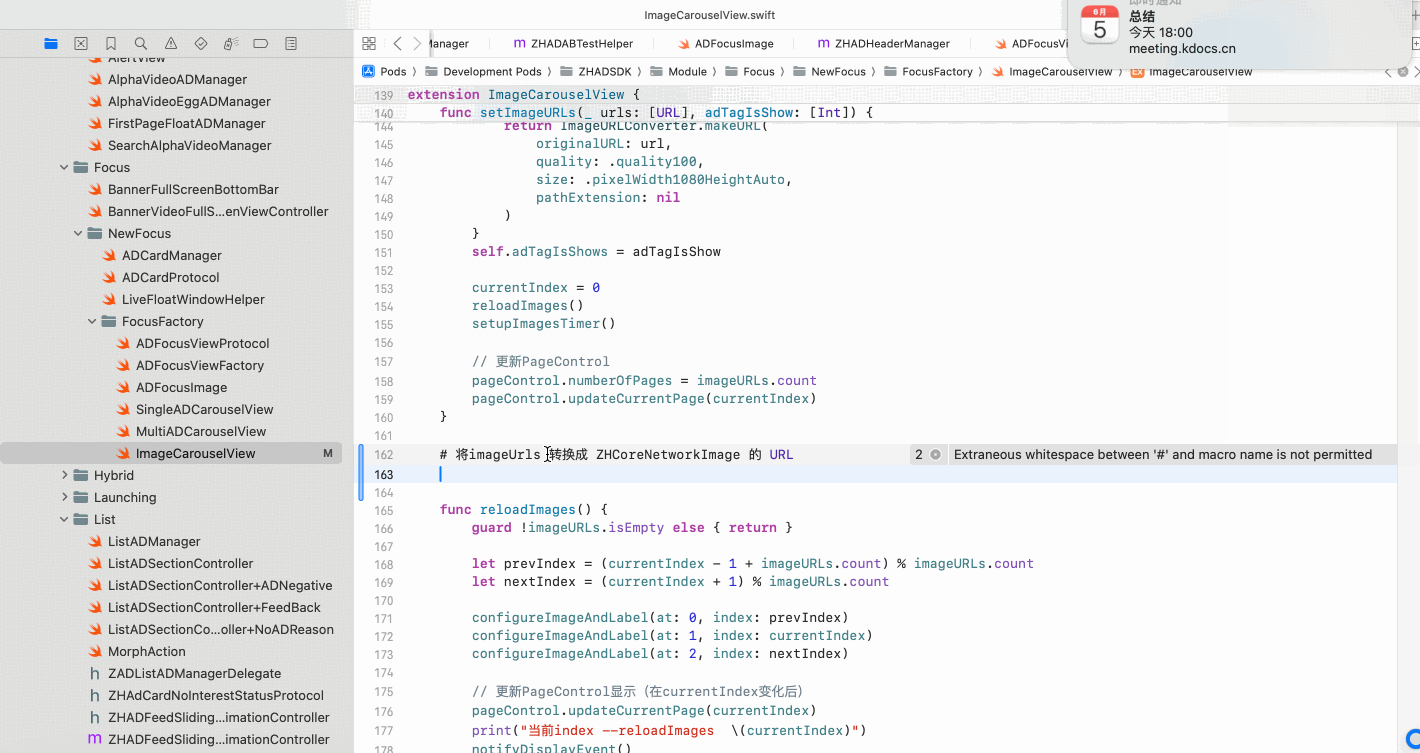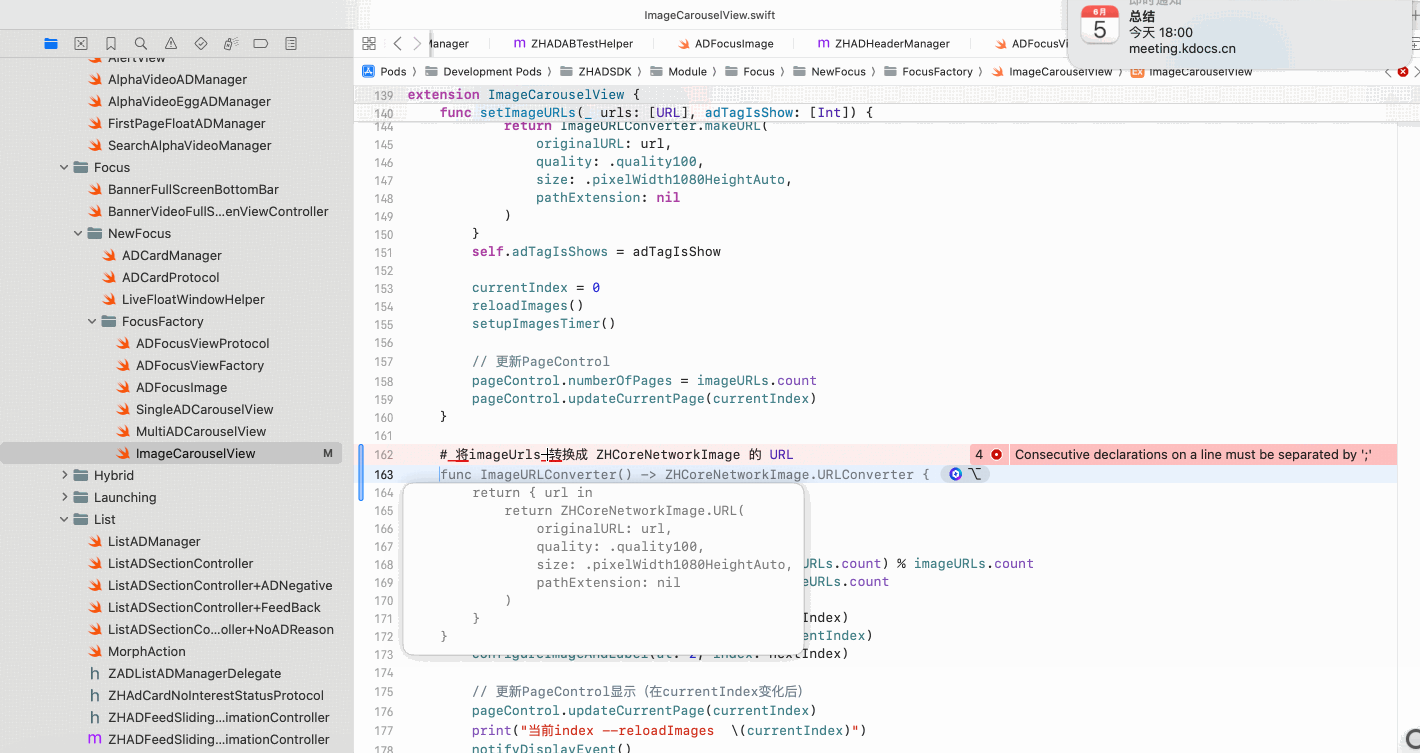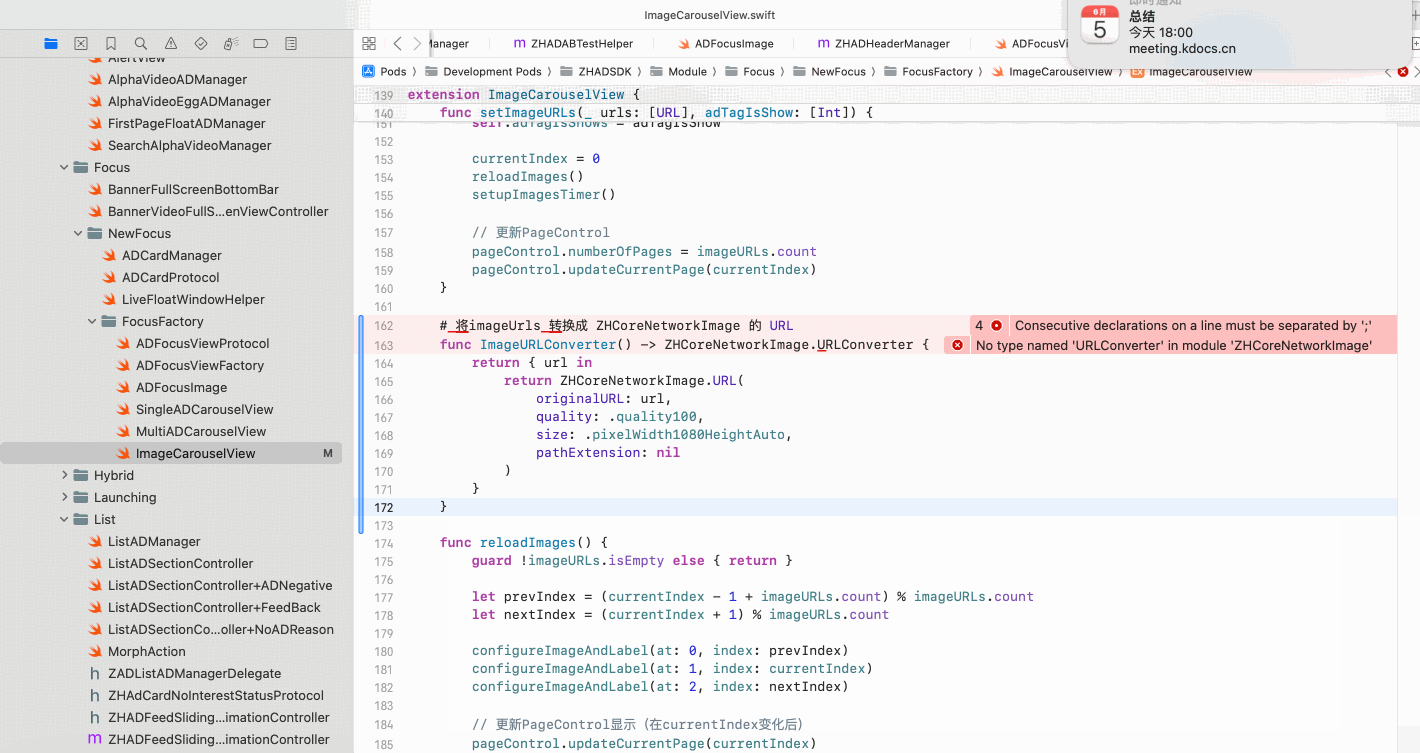
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
