深入理解算法的时间复杂度
文章目录
- 时间复杂度的定义
- 时间复杂度的分类
- 时间复杂度分析
- 常见数据结构和算法的时间复杂度
- 常见数据结构
- 常见算法
- 常见排序算法说明
- 冒泡排序(Bubble Sort)
- 快速排序(Quick Sort)
- 归并排序(Merge Sort)
- 堆排序(Heap Sort)
时间复杂度的定义
时间复杂度就是一种用来描述算法在输入规模增长时所需执行时间的度量,即描述算法运行时间随问题规模增加而增长的速度,它是对算法执行时间的上界估计,通常通过O符号表示。时间复杂度描述了算法的效率和执行速度,可以用来对比不同算法的性能。
备注:
1.时间复杂度描述的是算法在最坏情况下的运行时间。这是因为最坏情况下的时间复杂度是对算法性能的上界估计,能够保证算法在任何情况下都能在该时间范围内完成。
2.在实际的算法分析中,通常还考虑最好情况和平均情况下的时间复杂度。最好情况是指在最理想的输入情况下的时间复杂度,平均情况是对所有可能输入情况下的平均时间复杂度的估计。
时间复杂度的分类
时间复杂度粗略的分为两类: 多项式量级和非多项式量级
非多项式量级只有两个
O ( 2 n ) 和 O ( n ! ) O(2^n) 和 O(n!) O(2n)和O(n!)
非多项式量级算法的执行时间会随着输入规模的增加急剧增长,是非常低效的算法。
多项式量级的复杂度常见的并不多,从低阶到高阶有(越高阶的时间复杂度,执行效率越低):
O ( 1 ) < O ( l o g n ) < O ( n ) < O ( n l o g n ) < O ( n 2 ) O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) O(1)<O(logn)<O(n)<O(nlogn)<O(n2)
对应的曲线图如下图所示:

时间复杂度分析
1.我们在分析一个算法、一段代码的时间复杂度的时候,只需关注循环执行次数最多的那一段代码就可以了,它就代表着这个算法的时间复杂度。
2.加法法则:多个算法顺序追加使用的时候,总复杂度等于量级最大的那段代码的复杂度
3.乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
常见数据结构和算法的时间复杂度
常见数据结构
1.数组(Array)
- 索引访问: O(1)
- 查找: O(n)
- 插入/删除(末尾): O(1)
- 插入/删除(中间或开头): O(n)
2.链表(Linked List)
- 访问: O(n)
- 查找: O(n)
- 插入/删除(在头部进行): O(1)
- 插入/删除(在中间或末尾进行): O(1)(如果已知位置),O(n)(如果需要搜索位置)
3.栈(Stack)
- 插入/删除(在顶部): O(1)
- 访问,查找: O(n)
4.队列(Queue)
- 插入/删除(在头部或尾部进行): O(1)
- 访问: O(n)
5.哈希表(Hash Table):
- 插入/删除/访问(平均情况): O(1)
- 最坏情况下可能是O(n),取决于哈希冲突的数量
常见算法
1.线性搜索
- 时间复杂度:O(n)
2.二分查找
- 时间复杂度:O(logn)
3.冒泡排序
- 平均情况和最坏情况: O(n^2)
4.快速排序(Quick Sort)
- 平均情况: O(nlogn)
- 最坏情况: O(n^2)
5.归并排序(Merge Sort)
- 最好情况、平均情况和最坏情况: O(nlogn)
6.堆排序(Heap Sort)
- 平均情况和最坏情况: O(nlogn)
常见排序算法说明
注: 排序算法的稳定性是指在排序过程中,具有相等键值的元素在排序后的结果中,相对顺序保持不变的性质。稳定性是排序算法中一个重要的性质,因为在某些应用场景中,我们希望保持相等元素的相对顺序不变。稳定性的好处是可以确保排序算法在特定情况下的正确性,特别是在应对某些有依赖顺序的问题时。但是,并不是所有的排序算法都是稳定的,一些排序算法可能会改变具有相等键值的元素的相对顺序。因此,在选择排序算法时,需要根据具体的应用场景考虑排序算法的稳定性需求。
冒泡排序(Bubble Sort)
原理: 冒泡排序通过多次遍历数组,比较相邻元素的大小并交换位置,直到排序完毕。每一次遍历都会将最大的元素"冒泡"到末尾。
特点: 冒泡排序是一种比较简单的排序算法,实现起来容易理解,但效率较低。它的时间复杂度为O(n^2),适用于小规模的数据排序。
适合解决的问题:冒泡排序适合用于排序较小规模的数据,而不适合处理大规模的数据。
快速排序(Quick Sort)
原理: 快速排序是基于分治法的思想。它首先选择一个基准元素(通常是数组中的某个元素),然后将数组分割成两个子序列,其中一个子序列的元素都小于等于基准元素,另一个子序列的元素都大于等于基准元素。然后递归地对这两个子序列进行快速排序。
特点: 快速排序是一种基于比较的排序算法,它的平均时间复杂度为O(nlogn)。它具有原地排序和不稳定性的特点。
适合解决的问题:快速排序适用于大规模数据的排序,速度较快。它在实践中广泛应用于各种排序场景。
归并排序(Merge Sort)
原理: 归并排序也是基于分治法的思想。它将数组不断地分割成较小的子数组,然后将这些子数组逐个合并,直到排序完成。
特点: 归并排序的时间复杂度为O(nlogn),具有稳定性和可靠性的特点。它需要额外的空间来存储临时的中间结果数组。
适合解决的问题:归并排序适用于大规模数据的排序,稳定性和可靠性使其适用于需要保持相同元素顺序的场景。
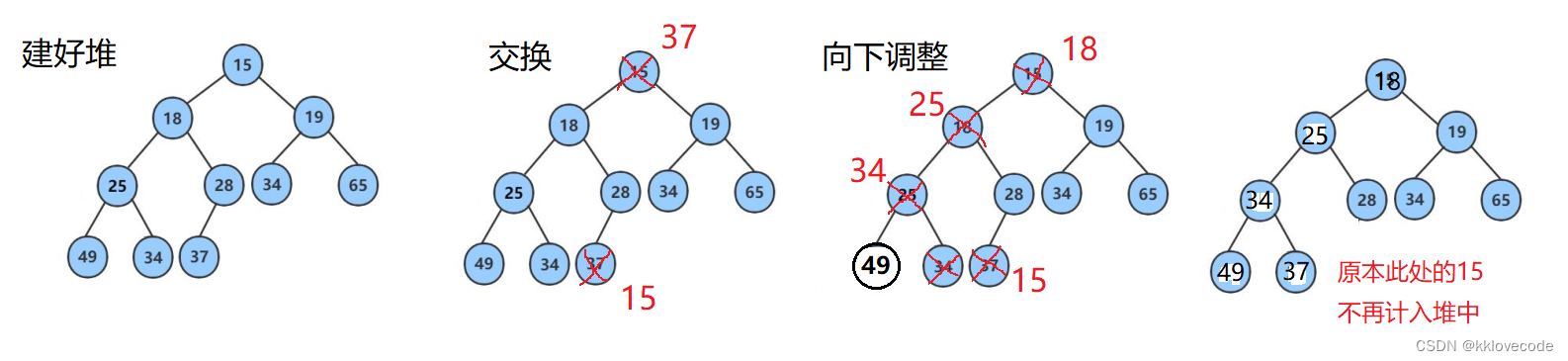
堆排序(Heap Sort)
原理: 堆排序基于完全二叉堆结构。它将待排序的数组构建成一个最大堆(或最小堆),然后不断地从最大堆中取出堆顶元素并调整堆,直到所有元素有序。
特点: 堆排序的时间复杂度为O(nlogn),它是一种原地排序算法,不需要额外的空间。但堆排序不是稳定的排序算法。
适合解决的问题: 堆排序适用于大规模数据的排序,特别适用于需要只保留部分最大(或最小)元素的场景。它在优先队列和求TopK问题中有广泛应用。
这些排序算法在实际应用中都有各自的应用场景和限制,选择正确的排序算法取决于数据规模、稳定性要求、空间复杂度要求和性能需求等因素。
冒泡排序由于性能很差,在实际工程中应用较少。
在对速度和空间复杂度有要求但对稳定性没要求的时候排序算法选用快速排序;
对稳定性有要求,但是对空间复杂度没有要求的时候排序算法选用归并排序;
在只需要保留最大/最小元素的应用场景下选用堆排序。
相关文章:

深入理解算法的时间复杂度
文章目录 时间复杂度的定义时间复杂度的分类时间复杂度分析常见数据结构和算法的时间复杂度常见数据结构常见算法 常见排序算法说明冒泡排序(Bubble Sort)快速排序(Quick Sort)归并排序(Merge Sort)堆排序(Heap Sort) 时间复杂度的定义 时间复杂度就是一种用来描述算法在输入规…...
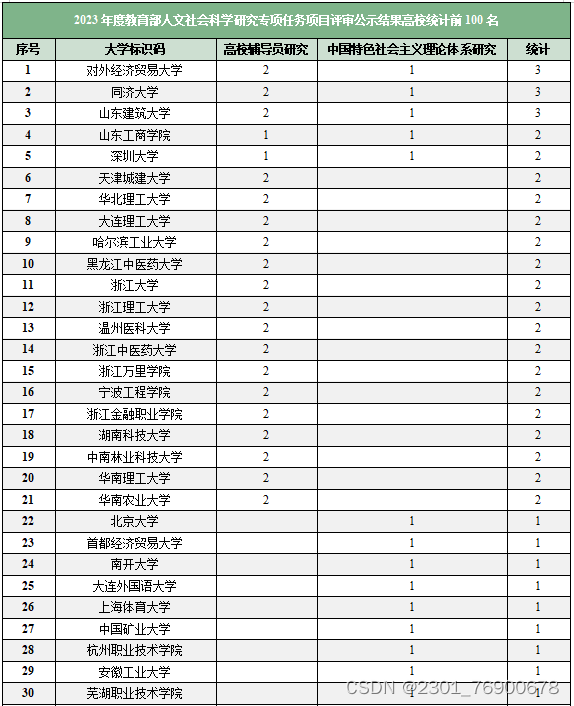
2023年度教育部人文社会科学研究一般项目评审结果,已公布!
【SciencePub学术】 9月15日,教育部社科司公示了2023年度教育部人文社会科学研究一般项目评审结果,共3482项。 其中,规划基金、青年基金、自筹经费项目共3029项通过专家评审;西部和边疆地区项目200项,新疆项目20项&a…...
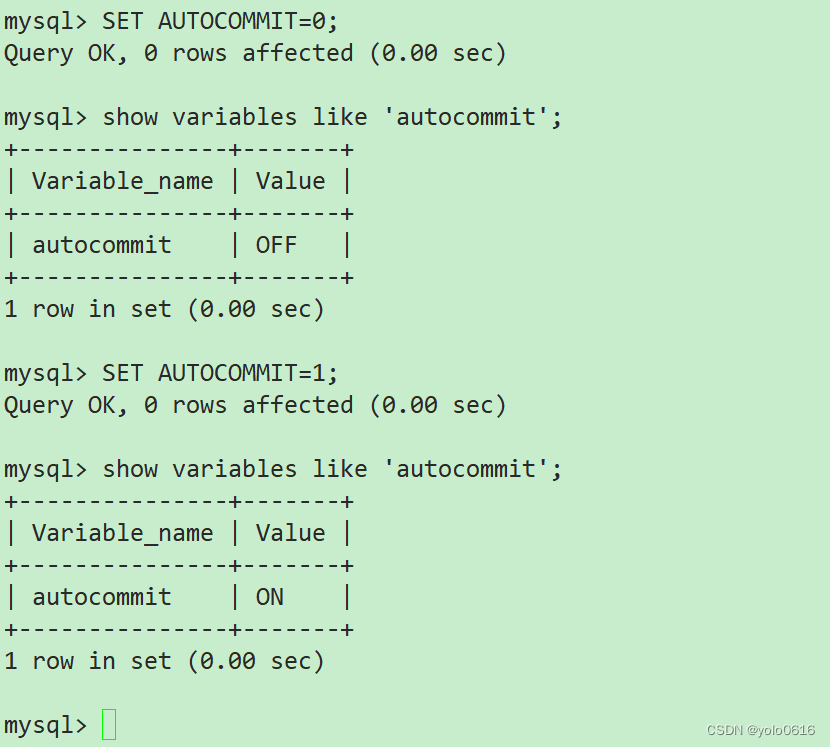
十一、MySql的事务(上)
文章目录 一、引入(一)CURD不加控制,会有什么问题?(二)CURD满足什么属性,能解决上述问题? 二、什么是事务?三、事务的特性(一)原子性:…...

时间序列分析1--生成和导出时间序列数据
时间序列数据的生成 直接录入 1.行录入 ts.(price,startc(2015,1),frequency 12) # price为时间序列变量,start为起始读入时间 frequncy指定每年读入的数据的频率,frequncy4为季度数据、frequncy52为星期数据 2.列录入 scan() 1:101 ....6:7 7:…...
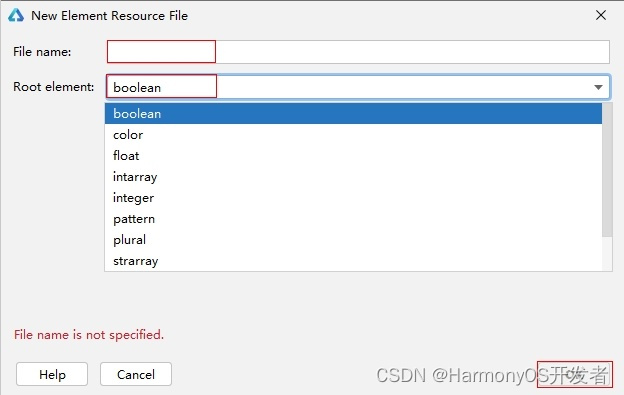
HarmonyOS应用开发—资源分类与访问
应用开发过程中,经常需要用到颜色、字体、间距、图片等资源,在不同的设备或配置中,这些资源的值可能不同。 应用资源:借助资源文件能力,开发者在应用中自定义资源,自行管理这些资源在不同的设备或配置中的表…...

C++中的转换构造函数
在 C/C++ 中,不同的数据类型之间可以相互转换。无需用户指明如何转换的称为自动类型转换(隐式类型转换),需要用户显式地指明如何转换的称为强制类型转换。 自动类型转换示例: int a = 6;a = 7.5 + a; 编译器对 7.5 是作为 double 类型处理的,在求解表达式时,先将 a 转换…...
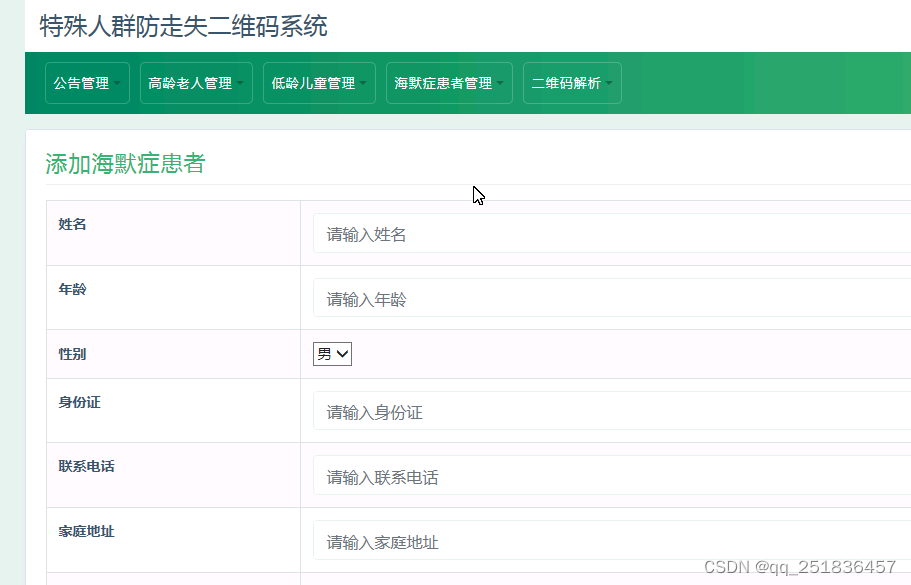
JSP ssm 特殊人群防走失系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 JSP ssm 特殊人群防走失系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源 代码和数据库,系统主要…...
怎么实现一个登录时需要输入验证码的功能
今天给项目换了一个登录页面,而这个登录页面设计了验证码,于是想着把这个验证码功能实现一下吧。 这篇文章就如何实现登录时的验证码的验证功能结合代码进行详细地介绍,以及介绍功能实现的思路。 目录 页面效果 实现思路 生成验证码的控制…...

在android工程中新建Android模块报错
复制了复制正常的build.gradle文件,然后把theme里面的东西改成了下面这个样就好了 <resources xmlns:tools"http://schemas.android.com/tools"><!-- Base application theme. --><style name"Theme.JiQuan" parent"Theme…...
电脑桌面的复选框如何取消
电脑桌面图标的复选框如何取消 1. 概述2. 去掉图标的复选框方法结束语 1. 概述 当你拿到新的电脑开机后,发现桌面上软件应用的图标左上角有个小框,每次点击图标都会显示,并且点击图标时,小框还会打上√; 这个小框的…...

【Unity每日一记】资源加载相关和检测相关
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...
【数据结构】长篇详解堆,堆的向上/向下调整算法,堆排序及TopK问题
文章目录 堆的概念性质图解 向上调整算法算法分析代码整体实现 向下调整算法算法分析整体代码实现 堆的接口实现初始化堆销毁堆插入元素删除元素打印元素判断是否为空取首元素实现堆 堆排序创建堆调整堆整合步骤 TopK问题 堆的概念 堆就是将一组数据所有元素按完全二叉树的顺序…...

DAQ高频量化平台:引领Ai高频量化交易模式变革
近年来,数字货币投资市场掀起了一股热潮,以(BTC)为代表的区块链技术带来了巨大的商业变革。数字资产的特点,如无国界、无阶级、无门槛、高流动性和高透明度,吸引了越来越多的人们的关注和认可,创…...

vue3 element plus获取el-cascader级联选择器选中的当前结点的label值 附vue2获取当前label
各位大佬,有时我们在处理级联选择组件数据时,不仅需要拿到id,还需要拿到label名称,但是通常组件直接绑定的是id,所以就需要我们用别的方法去拿到label,此处官方是有这个方法的,具体根据不同的element 版本进行分别处理。 VUE3 e…...
Spring Boot常见面试题
Spring Boot简介 Spring Boot 是由 Pivotal 团队提供,用来简化 Spring 应用创建、开发、部署的框架。它提供了丰富的Spring模块化支持,可以帮助开发者更轻松快捷地构建出企业级应用。Spring Boot通过自动配置功能,降低了复杂性,同…...

分块矩阵求逆
另可参考Block matrix on Wikipedia2018.4.3 补充补充两个参考文献,都是对工科很实用的矩阵手册:D. S. Bernstein, Matrix mathematics: Theory, facts, and formulas with application to linear systems theory. Princeton, NJ: Princeton University …...
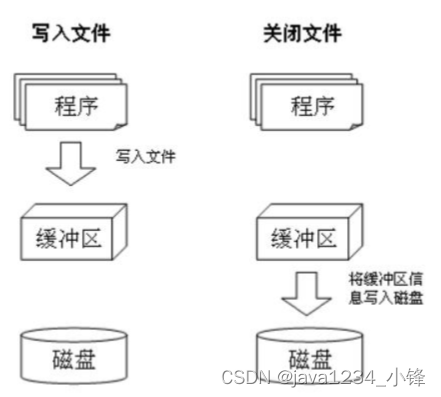
Python 文件写入操作
视频版教程 Python3零基础7天入门实战视频教程 w模式是写入,通过write方法写入内容。 # 打开文件 模式w写入,文件不存在,则自动创建 f open("D:/测试3.txt", "w", encoding"UTF-8")# write写入操作 内容写入…...

【Spring Boot系列】- Spring Boot侦听器Listener
【Spring Boot系列】- Spring Boot侦听器Listener 文章目录 【Spring Boot系列】- Spring Boot侦听器Listener一、概述二、监听器Listener分类2.1 监听ServletContext的事件监听器2.2 监听HttpSeesion的事件监听器2.3 监听ServletRequest的事件监听器 三、SpringMVC中的监听器3…...
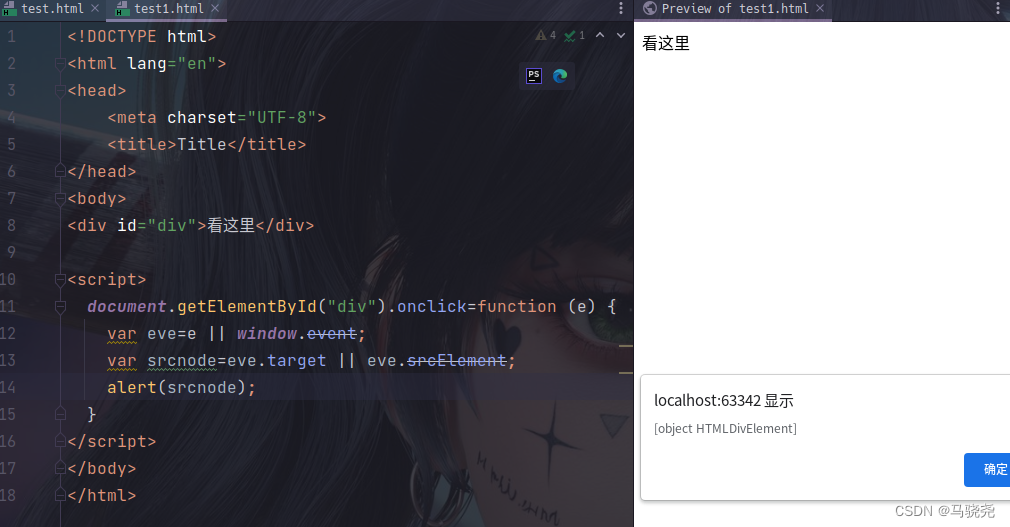
JavaScript速成课—事件处理
目录 一.事件类型 1.窗口事件 2.表单元素事件 3.图像事件 4.键盘事件 5.鼠标事件 二.JavaScript事件处理的基本机制 三.绑定事件的方法 1.DOM元素绑定 2.JavaScript代码绑定事件 3.监听事件函数绑定 四.JavaScript事件的event对象 1.获取event对象 2.鼠标坐标获取…...
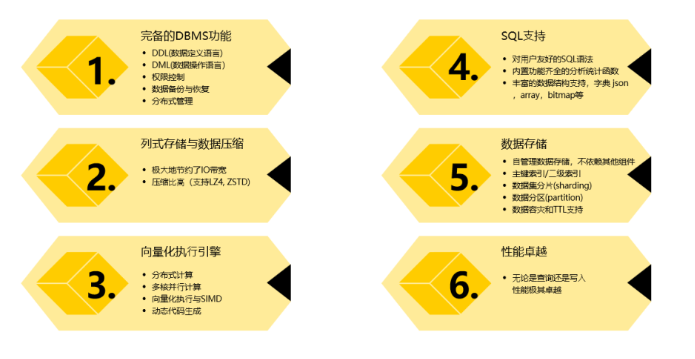
【入门篇】ClickHouse最优秀的开源列式存储数据库
文章目录 一、什么是ClickHouse?OLAP场景的关键特征列式数据库更适合OLAP场景的原因输入/输出CPU 1.1 ClickHouse的定义与发展历程1.2 ClickHouse的版本介绍 二、ClickHouse的主要特性2.1 高性能的列式存储2.2 实时的分析查询2.3 高度可扩展性2.4 数据压缩2.5 SQL支…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
