道路空间功率谱密度与时间功率谱密度(笔记)
0.随机路面
仿真时间200秒
车速15m/s
采样间隔0.25秒(4Hz)
A级路面平均振幅:0.0044米
B级路面平均振幅:0.0087米
C级路面平均振幅:0.0173米
D级路面平均振幅:0.0346米
1.先上代码其中之一
clc
clear
close all
%%
SimTime=200;
dt=0.01;%仿真步长
time=0:dt:SimTime;
sim_step = length(time);
Nt=length(time); % 采样点(可能要修改)
u=10; % m/s
df=1/(Nt*dt); % 采样频率间隔
f=0:df:1/(2*dt); % 采用频率一半(可修改)
nf=length(f); % 采样点的个数
n=f/u; % 采样空间频率,F是浮动的,随车速的改变而改变
%获得标准空间路面谱,A级
Pa=LMP(16,nf,n);
pa=Pa/u; % 转化为频谱
%获得标准空间路面谱,B级
Pb=LMP(64,nf,n);
pb=Pb/u; % 转化为频谱
%获得标准空间路面谱,C级
Pc=LMP(256,nf,n);
pc=Pc/u; % 转化为频谱
%获得标准空间路面谱,D级
Pd=LMP(1024,nf,n);
pd=Pd/u; % 转化为频谱
%%
%1输出标准路面空间频率谱G(n),结果与车速、SimTime、dt无关
figure(1)
loglog(n,Pa); %1输出标准路面空间频率谱G(n)
hold on
loglog(n,Pb);
hold on
loglog(n,Pc);
hold on
loglog(n,Pd);
xlabel('空间频率n[1/m]')
ylabel('路面不平度位移功率谱密度Gq(n)[m^3]')
legend('A','B','C','D')%2输出时间频率谱G(f),结果与车速有关
% figure(2)
% loglog(f,pa)
% hold on
% loglog(f,pb)
% hold on
% loglog(f,pc)
% hold on
% loglog(f,pd)
% xlabel('时间频率[Hz]')
% ylabel('G(f)[m^2/Hz]') % 2输出时间频率谱G(f)
% legend('A','B','C','D')2.参考链接
链接1
链接2
链接3
3.笔记
Sine_RoadRoughnessGradeClassCal_230713.m中:
3.1. 降SimTime可以降等级,升omiga会使改线条等级范围变大,降车速可降等级
但是在时间-输入关系不变的情况下,低车速对应高空间频率路面,高车速对应低空间频率路面
代码一:SimTime=20/4;dt=0.01;omiga=2pi1.5;A=0.05;V=18;
%%
%1.正弦路面
SimTime=20/4;
dt=0.01;%仿真步长
time=0:dt:SimTime;
sim_step = length(time);
omiga=2*pi*1.5;
A=0.05;%振幅
Z1=A*sin(time*omiga);%路面高程值
Z_p1 =A*cos(time*omiga)*omiga;%路面高程值导数
x=Z1;Nt=length(x); % 采样点(可能要修改)
V=18; % km/h
结果C级路面

注意此图中的标准等级路面PSD-(1/n)函数线条与汽车理论208页图6-5一致
代码一点五:SimTime=20;dt=0.01;omiga=2*pi;A=0.05;V=18;
%%
%1.正弦路面
SimTime=20;
dt=0.01;%仿真步长
time=0:dt:SimTime;
sim_step = length(time);
omiga=2*pi;
A=0.05;%振幅
Z1=A*sin(time*omiga);%路面高程值
Z_p1 =A*cos(time*omiga)*omiga;%路面高程值导数
x=Z1;Nt=length(x); % 采样点(可能要修改)
V=18; % km/h
结果B级路面

代码二:SimTime=20/2;dt=0.01;omiga=2pi2;A=0.019;V=18;
SimTime=20/2;
dt=0.01;%仿真步长
time=0:dt:SimTime;
sim_step = length(time);
omiga=2*pi*2;
A=0.019;
Z1=A*sin(time*omiga);%路面高程值
Z_p1 =A*cos(time*omiga)*omiga;%路面高程值导数
x=Z1;
dt=0.01;
Nt=length(x); % 采样点(可能要修改)
V=18; % km/h
结果A级路面

代码二点五:SimTime=20/4;dt=0.01;omiga=2*pi;A=0.019;V=9;
SimTime=20/4;
dt=0.01;%仿真步长
time=0:dt:SimTime;
sim_step = length(time);
omiga=2*pi;
A=0.019;
Z1=A*sin(time*omiga);%路面高程值
Z_p1 =A*cos(time*omiga)*omiga;%路面高程值导数
x=Z1;
dt=0.01;
Nt=length(x); % 采样点(可能要修改)
V=9; % km/h
结果B级路面

相关文章:

道路空间功率谱密度与时间功率谱密度(笔记)
0.随机路面 仿真时间200秒 车速15m/s 采样间隔0.25秒(4Hz) A级路面平均振幅:0.0044米 B级路面平均振幅:0.0087米 C级路面平均振幅:0.0173米 D级路面平均振幅:0.0346米 1.先上代码其中之一 clc clear clo…...

JMeter接口测试之文件上传
最近用JMeter做接口测试,频繁遇到了文件上传的接口,与其他一般接口的处理方式不一样,想着分享下,希望能给测试同学一点启发。 文章将围绕三个部分进行展开: 一、用户场景 二、接口请求参数 三、JMeter脚本编写步骤…...
自动化测试需知的4项测试工具!
一般来说学自动化会建议大家先学selenium,因为最早的时候,自动化就代表selenium,进入测试行业就开始做接口测试,而且现在基本每个公司都需要接口测试。今天就和大家聊一下接口测试的工具。 一、Robot Framework 机器人框架。之所…...
【深度学习】clip-interrogator clip docker 容器启动过程
文章目录 dockerfile备忘ENTRYPOINT ["bash", "/app/startProject.sh"]常用docker指令web服务脚本访问接口文件 给一张图片,输出图片描述。 dockerfile备忘 只有从dockerfile制作的镜像才有分层结构,加速传输,故第一步…...

Linux设备驱动之gpio-keys
Linux设备驱动之gpio-keys 前两个章节介绍了Linux字符设备和platform设备的注册,他们都是比较基础的,让大家理解Linux内核的设备驱动是如何注册、使用的。但在工作中,个人认为完全手写一个字符设备驱动的机会比较少,更多的都是基…...
【vue3页面展示代码】展示代码codemirror插件
技术版本: vue 3.2.40、codemirror 6.0.1、less 4.1.3、vue-codemirror 6.1.1、 codemirror/lang-vue 0.1.2、codemirror/theme-one-dark 6.1.2 效果图: 1.安装插件 yarn add codemirror vue-codemirror codemirror/lang-vue codemirror/theme-one-dar…...
【面试必刷TOP101】链表相加 单链表的排序
目录 题目:链表相加(二)_牛客题霸_牛客网 (nowcoder.com) 题目的接口: 解题思路: 代码: 过啦!!! 题目:单链表的排序_牛客题霸_牛客网 (nowcoder.com) 题目的接口:…...
Visual Studio复制、拷贝C++项目与第三方库配置信息到新的项目中
本文介绍在Visual Studio软件中,复制一个已有的、配置过多种第三方库的C项目,将其拷贝为一个新的项目,同时使得新项目可以直接使用原有项目中配置好的各类**C**配置、第三方库等的方法。 在撰写C 代码时,如果需要用到他人撰写的第…...

rust迭代器
迭代器用来遍历容器。 迭代器就是把容器中的所有元素按照顺序一个接一个的传递给处理逻辑。 Rust中的迭代器 标准库中定义了Iterator特性 trait Iterator {type Item;fn next(&mut self) -> Option<Self::Item>; }实现了Iterator特性的结构体就是迭代器。 很多类…...
软件定制开发的优势与步骤|APP搭建|小程序
软件定制开发的优势与步骤|APP搭建|小程序 定制开发的优势: 1. 满足特定需求:定制开发可以根据客户的实际需求进行设计和开发,使得软件系统能够更好地满足客户的业务目标。 2. 优化用户体验:通过深入了解客户的需求,定…...
ERR_CONNECTION_REFUSED等非标准的HTTP错误状态码原因分析和解决办法
文章目录 一、DNS Resolution Failed1,DNS服务器故障2,DNS配置错误3,DNS劫持4,域名过期-5,其他网络问题 二、ERR_CONNECTION_REFUSED-"ERR_CONNECTION_REFUSED" 错误可能有多种原因 三、ERR_SSL_PROTOCOL_ER…...

瀑布流 - Vue3基于Grid布局简单实现一个瀑布流组件
瀑布流 - Vue3基于Grid布局简单实现一个瀑布流组件 前言 在学习Grid布局之时,我发现其是CSS中的一种强大的布局方案,它将网页划分成一个个网格,可以任意组合不同的网格,做出各种各样的布局,在刷某书和某宝首页时&…...

ES6面试题总结
1. 谈谈你对 ES6 的理解,为什么要学习es6? ES6是新一代的JS语言标准,对分JS语言核心内容做了升级优化,规范了JS使用标准,新增了JS原生方法,使得JS使用更加规范,更加优雅,更适合大型应用的开发。学习ES6是成…...

mybatisplus,jdbc 批量插入
1.测试用例 项目中遇到在做导入号码的时候我们会用到批量导入,提高入库的速度。接下来我们以10000条为测试用例。 1.1 批量执行sql语句 当需要成批插入或者更新记录时,可以采用Java的批量更新机制,这一机制允许多条语句一次性提交给数据库…...
如何使用IP归属地查询API来追踪网络活动
引言 在当今数字化世界中,了解网络活动的源头和位置对于网络安全、市场研究和用户体验至关重要。IP归属地查询API是一种强大的工具,可以帮助您追踪网络活动并获取有关IP地址的重要信息。本文将探讨如何使用IP归属地查询API来追踪网络活动,以…...

【SQL】S0 系列博文大纲
系列博文大纲 SQL 学习环境建议系列博文相关书籍系列博文大纲阶段进展 SQL 学习环境建议 对于 SQL 语言的学习,博主本地使用:MySQL DataGrip; MySQL 提供本地数据库服务; DataGrip IDE,承担编程运行测试任务…...
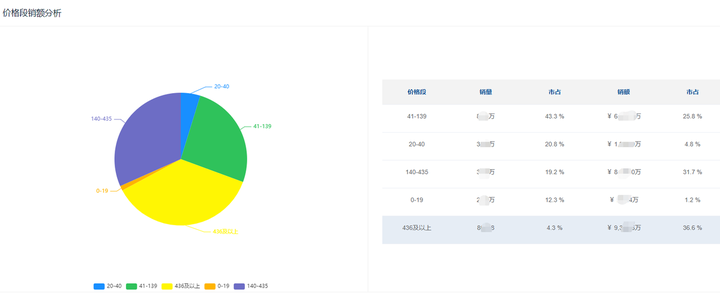
2023年8月体育用品行业数据分析(京东数据产品)
当前,亚运会临近,这也带动了国民对体育消费的热情,体育产品内销逐渐旺盛,“亚运经济”红利开始显现。鲸参谋数据显示,今年8月份,京东平台上体育用品行业的销量为185万,同比增长2%;销…...

国内高校镜像网站
国内各大高校开源镜像站 排名不分前后 清华大学:https://mirrors.tuna.tsinghua.edu.cn/ 北京大学:https://mirrors.pku.edu.cn/ 北京外国语大学:http:// https://mirrors.bfsu.edu.cn/ 北京理工大学:https://mirrors.bit.e…...
Linux安装kafka-manager
相关链接https://github.com/yahoo/kafka-manager/releases kafka-manager-2.0.0.2下载地址 百度云链接:https://pan.baidu.com/s/1XinGcwpXU9YBF46qkrKS_A 提取码:tzvg 一、安装部署 1.把kafka-manager-2.0.0.2.zip拷贝到目录 /opt/app/elk 2.解压…...

MYSQL索引——B+树讲解
B-/B树看 MySQL索引结构 B-树 B-树,这里的 B 表示 balance( 平衡的意思),B-树是一种多路自平衡的搜索树.它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。下图是 B-树的简化图. B-树有如下特点: 所有键值分布在整颗树中; 任何一…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
