剑指 Offer 42. 连续子数组的最大和
剑指 Offer 42. 连续子数组的最大和
难度:easy\color{Green}{easy}easy
题目描述
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
提示:
- 1<=arr.length<=1051 <= arr.length <= 10^51<=arr.length<=105
- −100<=arr[i]<=100-100 <= arr[i] <= 100−100<=arr[i]<=100
注意:本题与主站 53 题相同:https://leetcode-cn.com/problems/maximum-subarray/
算法
| 常见解法 | 时间复杂度 |
|---|---|
| 暴力搜索 | O(n2)O(n^2)O(n2) |
| 分治思想 | O(nlogn)O(nlogn)O(nlogn) |
| 动态规划 | O(n)O(n)O(n) |
(动态规划)
- 状态定义: 设动态规划列表 dpdpdp ,dp[i]dp[i]dp[i] 代表以元素 nums[i]nums[i]nums[i] 为结尾的连续子数组最大和。
为何定义最大和
dp[i]中必须包含元素nums[i]:保证dp[i]递推到dp[i+1]的正确性;如果不包含nums[i],递推时则不满足题目的 连续子数组 要求。
-
转移方程: 若 dp[i−1]≤0dp[i−1]≤0dp[i−1]≤0 ,说明 dp[i−1]dp[i−1]dp[i−1] 对 dp[i]dp[i]dp[i] 产生负贡献,即 dp[i−1]+nums[i]dp[i−1]+nums[i]dp[i−1]+nums[i] 还不如 nums[i]nums[i]nums[i] 本身大。
- 当 dp[i−1]>0dp[i−1]>0dp[i−1]>0 时:执行 dp[i]=dp[i−1]+nums[i]dp[i]=dp[i−1]+nums[i]dp[i]=dp[i−1]+nums[i] ;
- 当 dp[i−1]≤0dp[i−1]≤0dp[i−1]≤0 时:执行 dp[i]=nums[i]dp[i]=nums[i]dp[i]=nums[i] ;
-
初始状态: dp[0]=nums[0]dp[0]=nums[0]dp[0]=nums[0],即以 nums[0]nums[0]nums[0] 结尾的连续子数组最大和为 nums[0]nums[0]nums[0] 。
-
返回值: 返回 dpdpdp 列表中的最大值,代表全局最大值。
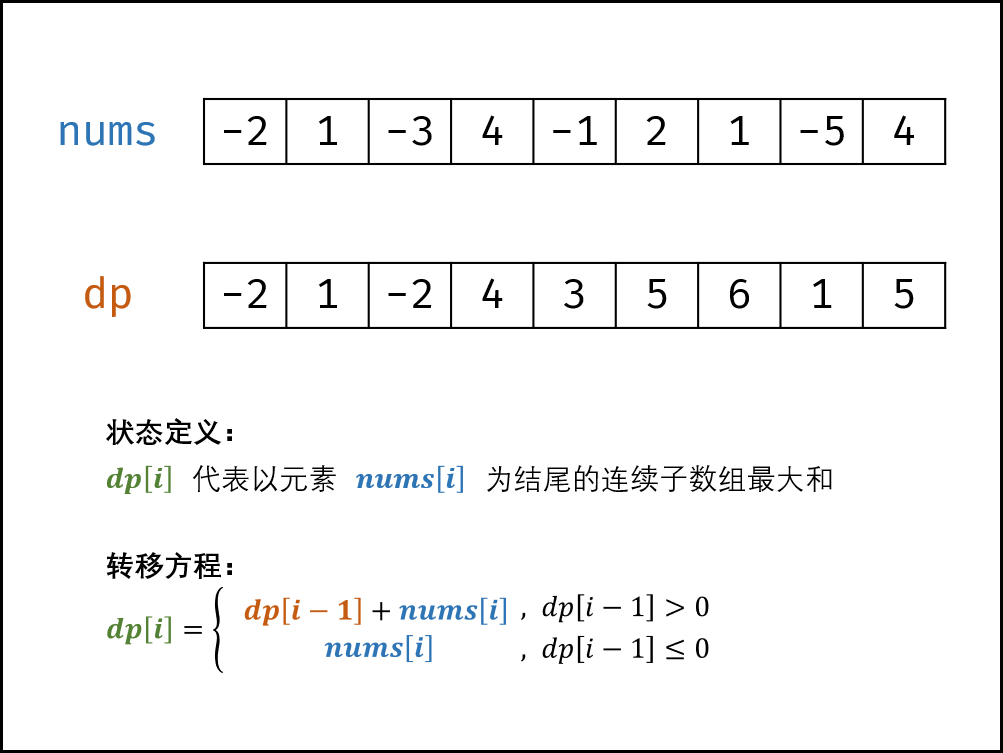
复杂度分析
-
时间复杂度:O(n)O(n)O(n)。
-
空间复杂度 : O(1)O(1)O(1)
C++ 代码
使用 res 代表最终的答案,s 表示前 i - 1 项的值, 如果前 i - 1 项的值小于 0,s 等于当前的数 num,如果大于 0, 说明可以加上当前的数字 num,继续往后运算。
class Solution {
public:int maxSubArray(vector<int>& nums) {int res = INT_MIN, s = 0;for (auto x : nums) {if (s < 0) s = 0;s += x;res = max(res, s);}return res;}
};
参考链接
相关文章:
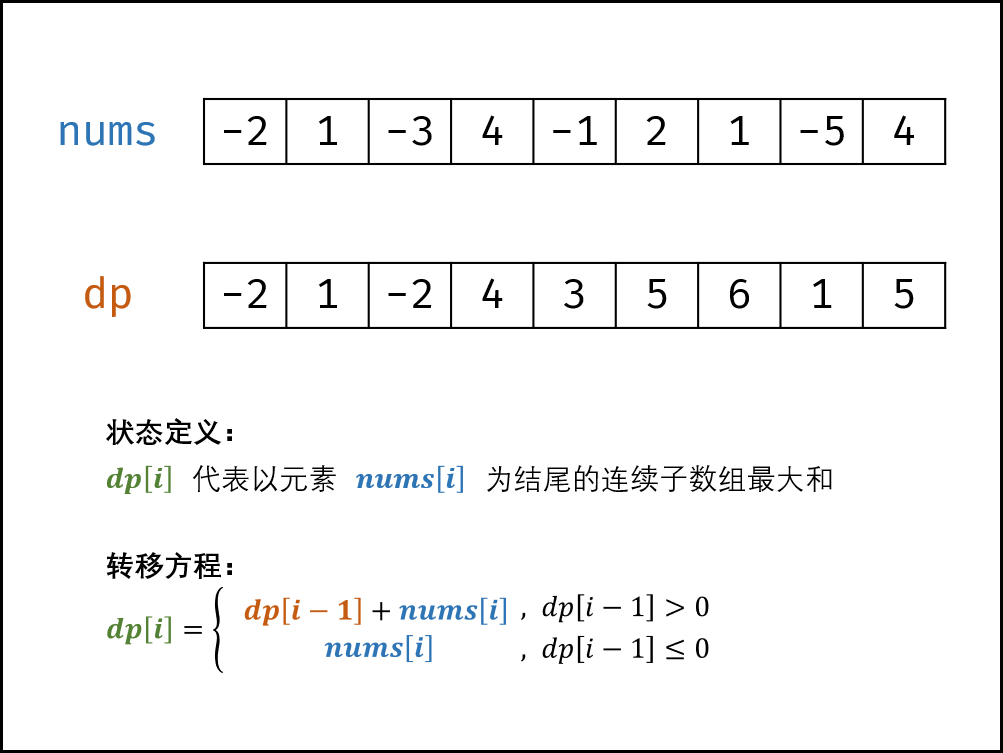
剑指 Offer 42. 连续子数组的最大和
剑指 Offer 42. 连续子数组的最大和 难度:easy\color{Green}{easy}easy 题目描述 输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。 要求时间复杂度为O(n)。 示例1: 输入: nums [-2,1,-3,4,-1,2,1,-5,4] 输…...

双指针 (C/C++)
1. 双指针 双指针算法的核心思想:将暴力解法的时间复杂度,通常是O(N*N),通过某种特殊的性质优化到O(N)。 做题思路:先想想暴力解法的思路,然后分析这道题的特殊性质,一般是单调性。然后得出双指针算法的思路…...
CVE-2023-23752 Joomla未授权访问漏洞分析
漏洞概要 Joomla 在海外使用较多,是一套使用 PHP 和 MySQL 开发的开源、跨平台的内容管理系统(CMS)。 Joomla 4.0.0 至 4.2.7 版本中的 ApiRouter.php#parseApiRoute 在处理用户的 Get 请求时未对请求参数有效过滤,导致攻击者可向 Joomla 服务端点发送包…...
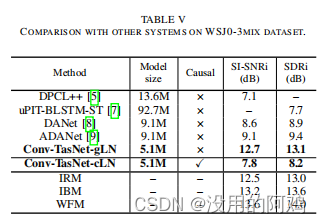
单通道说话人语音分离——Conv-TasNet(Convolutional Time-domain audio separation Network)
单通道说话人语音分离——Conv-TasNet模型(Convolutional Time-domain audio separation Network) 参考文献:《Conv-TasNet: Surpassing Ideal Time-FrequencyMagnitude Masking for Speech Separation》 1.背景 在真实的声学环境中,鲁棒的语音处理通常…...
)
华为OD机试真题Python实现【环中最长子串】真题+解题思路+代码(20222023)
环中最长子串 题目 给你一个字符串s,首尾相连成一个环形, 请你在环中找出o字符出现了偶数次最长子字符串的长度. 备注: 1 <= s.lenth <= 5x10^5 s只包含小写英文字母 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 输入是…...

Netcat安装与使用(nc)
Netcat安装与使用1.Netcat简介1.1.Netcat安装1.1.1.安装整体流程1.1.1.1.安装依赖1.1.1.2.安装Netcat1.1.1.3.配置环境变量1.1.1.4.测试1.2.Netcat基本功能1.3.Netcat常用参数2.Netcat用法2.1.前期准备2.2.banner相关信息抓取2.3.端口扫描2.3.1.扫描指定端口2.3.2.扫描指定端口…...
蓝桥杯:聪明的猴子
题目链接:聪明的猴子https://www.lanqiao.cn/problems/862/learning/ 目录 题目描述 输入描述 输出描述 输入输出样例 运行限制 解题思路: 最小生成树 AC代码(Java): 课后练习: 题目描述 在一个热带雨林中生存…...

Spring Boot应用如何快速接入Prometheus监控
1. Micrometer简介Micrometer为Java平台上的性能数据收集提供了一个通用的API,它提供了多种度量指标类型(Timers、Guauges、Counters等),同时支持接入不同的监控系统,例如Influxdb、Graphite、Prometheus等。可以通过M…...
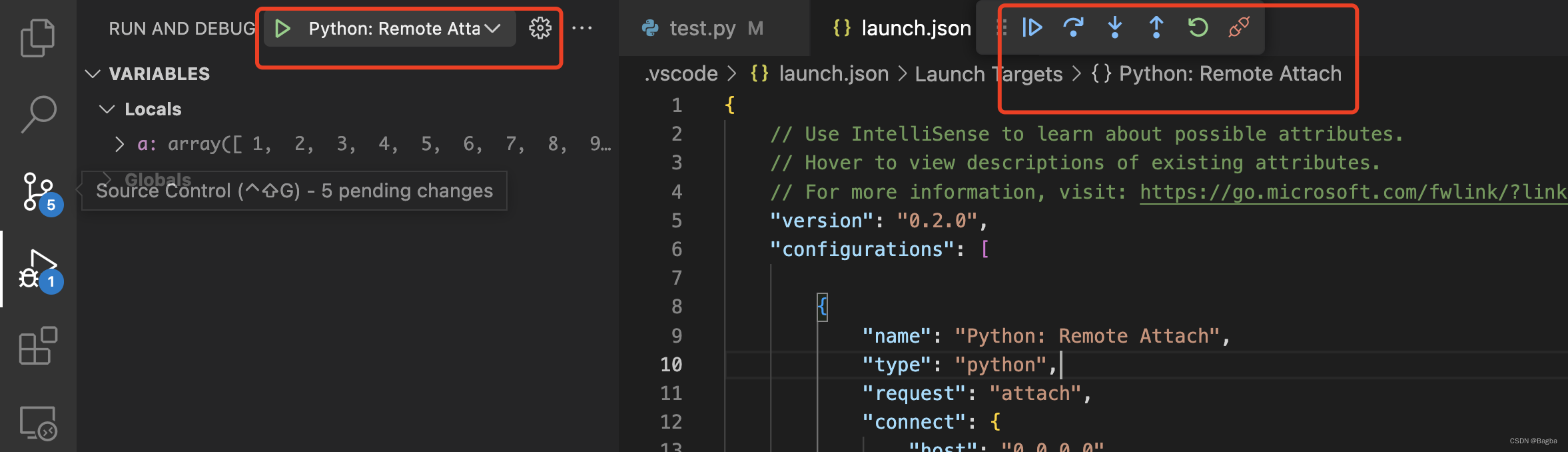
vscode远程调试python
目的 注意:这里我们想要实现的是:用vscode 使用remote ssh打开project,然后直接在project里面进行debug,而不需要 在本地vscode目录打开一样的project。 假设大家已经会使用remote ssh打开远程服务器的代码了,那么只…...
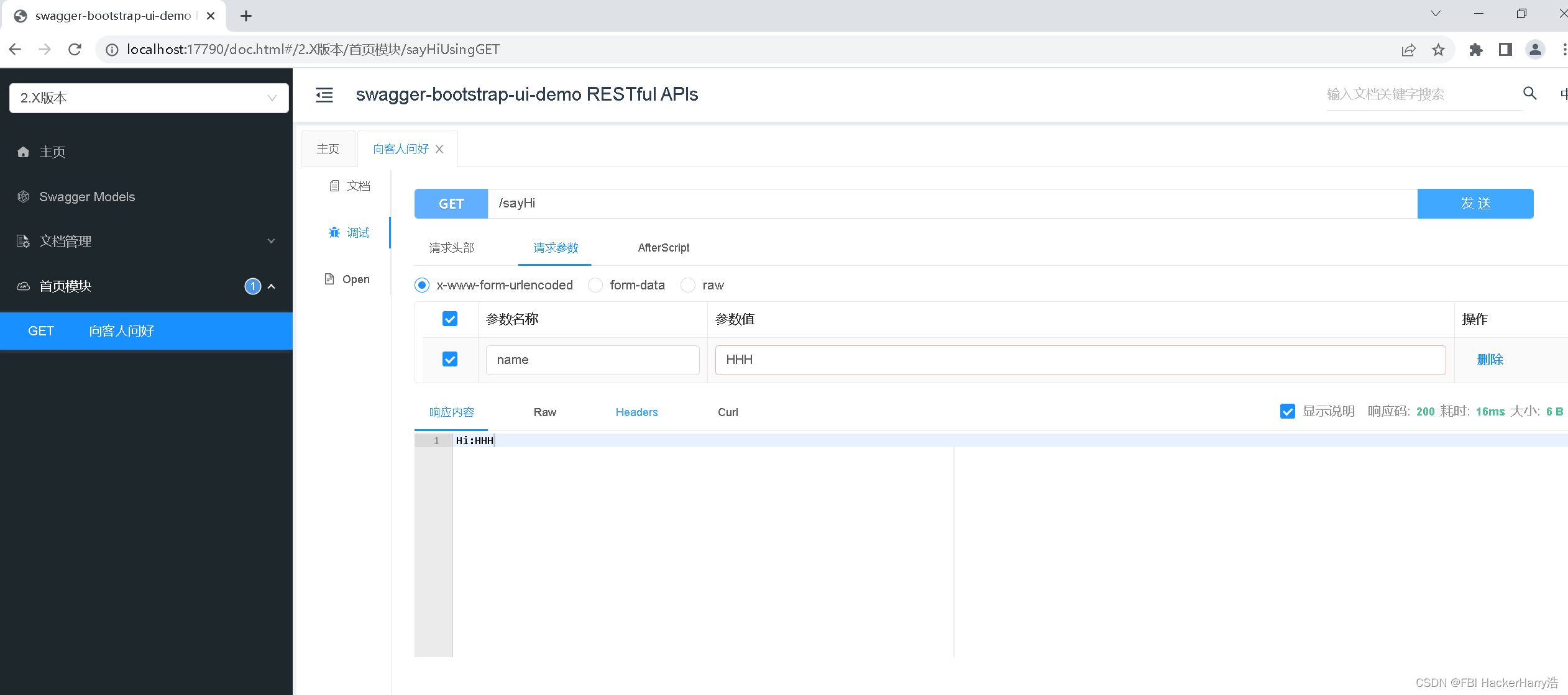
Spring Boot 框架 集成 Knife4j(内含源代码)
Spring Boot 框架 集成 Knife4j(内含源代码) 源代码下载链接地址:https://download.csdn.net/download/weixin_46411355/87480176 目录Spring Boot 框架 集成 Knife4j(内含源代码)源代码下载链接地址:[htt…...

什么蓝牙耳机适合打游戏?打游戏不延迟的蓝牙耳机
为了提升游戏体验,除了配置强悍的主机外,与之搭配蓝牙耳机等外设产品也尤为重要,今天就带大家来了解一下以下几款适合玩游戏,低延迟操作的蓝牙耳机。 第一款:南卡小音舱蓝牙耳机 参考价格:239元 推荐理由…...
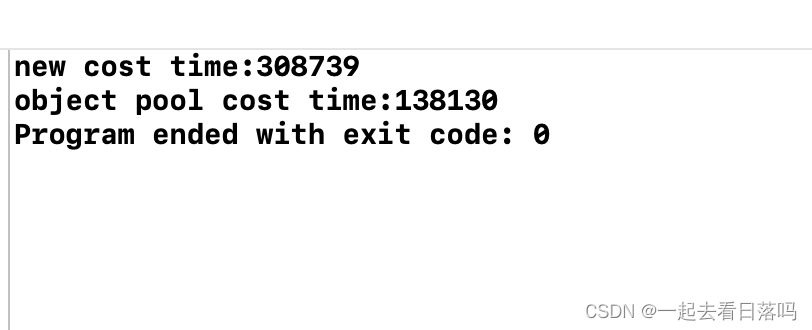
【项目设计】高并发内存池(一)[项目介绍|内存池介绍|定长内存池的实现]
🎇C学习历程:入门 博客主页:一起去看日落吗持续分享博主的C学习历程博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话: 也许你现在做的事情,暂时看不到成果,但不要忘记&…...
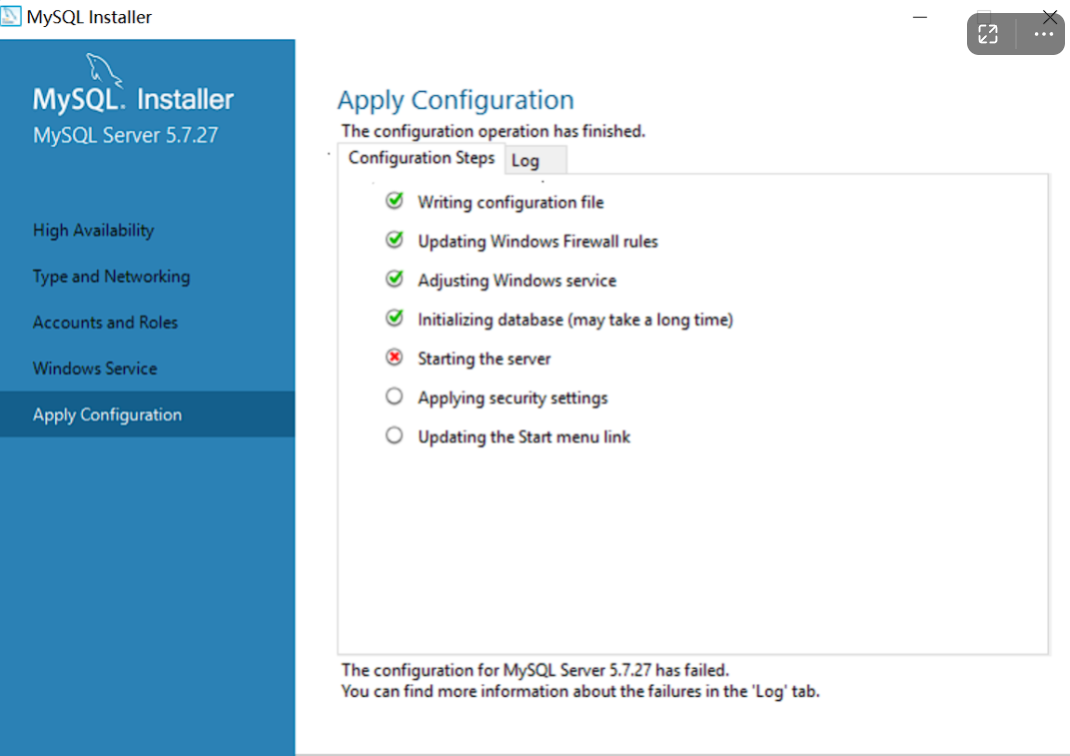
初识MySQL下载与安装【快速掌握知识点】
目录 前言 MySQL版本 MySQL类型 MySQL官网有.zip和.msi两种安装形式; MySQL 下载 1、MySQL 属于 Oracle 旗下产品,进入Oracle官网下载 2、点击产品,找到MySQL 3、进入MySQL页面 4、点击Download(下载)&#x…...
如何终止一个线程
如何终止一个线程 是使用 thread.stop() 吗? public class ThreadDemo extends Thread{Overridepublic void run() {try {Thread.sleep(10000);} catch (InterruptedException e) {e.printStackTrace();}System.out.println("this is demo thread :"Thre…...

上岸!选择你的隐私计算导师!
开放隐私计算 开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区”。183篇原创内容公众号…...
go gin学习记录5
有了前面几节的学习,如果做个简单的web服务端已经可以完成了。 这节来做一下优化。 我们实验了3种SQL写入的方法,但是发现每一种都需要在方法中去做数据库链接的操作,有些重复了。 所以,我们把这部分提取出来,数据库链…...
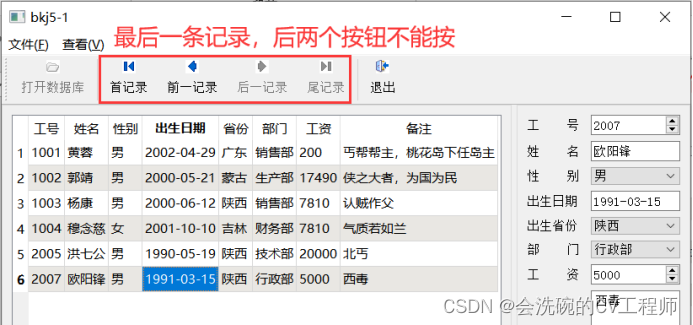
PyQt5数据库开发2 5.1 QSqlQueryModel
目录 一、Qt窗体设计 1. 新建Qt项目 2. 拷贝4-3的部分组件过来 3. 添加资源文件 4. 创建Action 5. 添加工具栏 6. 创建菜单项 7. 关闭Action的实现 8. 调整布局 8.1 调整两个groupbox的布局 8.3 为窗体设置全局布局 二、代码拷贝和删除 1. 新建项目目录 2. 编译…...

MySQL-redo log和undo log
什么是事务 事务是由数据库中一系列的访问和更新组成的逻辑执行单元 事务的逻辑单元中可以是一条SQL语句,也可以是一段SQL逻辑,这段逻辑要么全部执行成功,要么全部执行失败 举个最常见的例子,你早上出去买早餐,支付…...
阿里云ECS TOP性能提升超20%!KeenTune助力倚天+Alinux3达成开机即用的全栈性能调优 | 龙蜥技术
文/KeenTune SIG01阿里云 ECS 上售卖页新增“应用加速”功能2023年1月12日 阿里云 ECS 的售卖页有了一些新的变化,在用户选择倚天 Alinux3 新建实例时,多了一个新的选项“应用加速”。这个功能是 阿里云 ECS 基于 KeenTune 提供典型云场景的开机即用的全…...
)
华为OD机试真题Python实现【快递业务站】真题+解题思路+代码(20222023)
快递业务站 题目 快递业务范围有 N 个站点,A 站点与 B 站点可以中转快递,则认为 A-B 站可达, 如果 A-B 可达,B-C 可达,则 A-C 可达。 现在给 N 个站点编号 0、1、…n-1,用 s[i][j]表示 i-j 是否可达, s[i][j] = 1表示 i-j可达,s[i][j] = 0表示 i-j 不可达。 现用二维…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
