【算法】二分答案
文章目录
- 相关链接
- 什么时候使用二分答案?
- 题目列表
- 最大化最小化相关题目列表📕
- 2439. 最小化数组中的最大值
- 解法1——二分答案
- 解法2——分类讨论O(n)
- 2513. 最小化两个数组中的最大值(二分答案+lcm+容斥原理)🐂好题!
- 相似题目(容斥原理+二分查找)
- 878. 第 N 个神奇数字
- 1201. 丑数 III
- 2517. 礼盒的最大甜蜜度(二分答案)
相关链接
【力扣周赛】第 362 场周赛(⭐差分&匹配&状态压缩DP&矩阵快速幂优化DP&KMP)里面有一些二分答案的题目。
【力扣周赛】第 363 场周赛(完全平方数和质因数分解) T3是二分答案。
什么时候使用二分答案?
看到「最大化最小值」或者「最小化最大值」就要想到二分答案,这是一个固定的套路。
或者
答案不好直接求,但是可以判断某个数字是否可以满足题目要求且单调时。
具体看下面例题体会一下即可。
题目列表
最大化最小化相关题目列表📕
题目列表来源:https://leetcode.cn/problems/maximize-the-minimum-powered-city/solutions/2050272/er-fen-da-an-qian-zhui-he-chai-fen-shu-z-jnyv/

2439. 最小化数组中的最大值
https://leetcode.cn/problems/minimize-maximum-of-array/
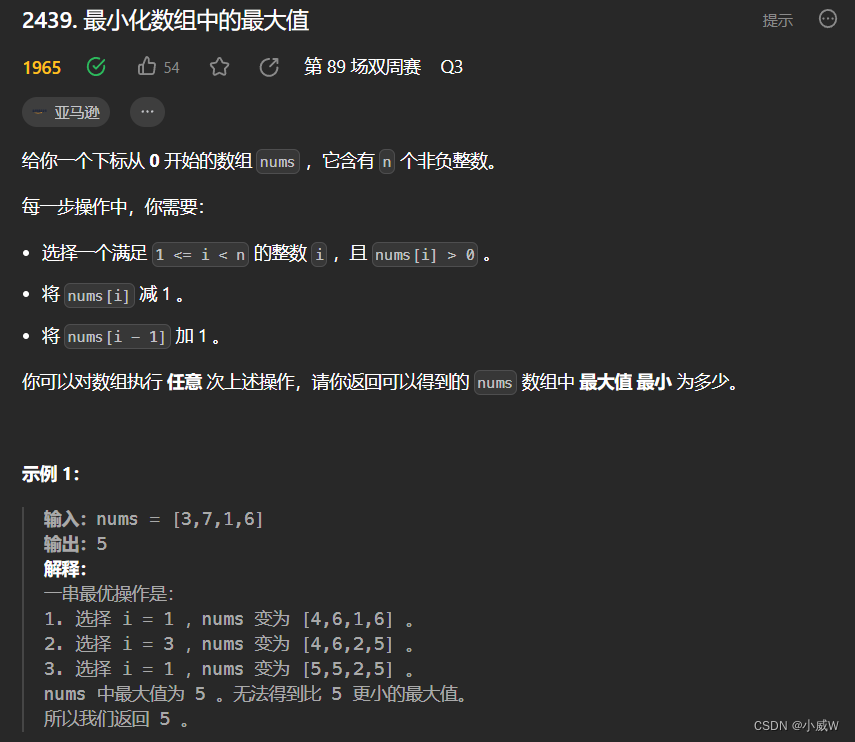
提示:
n == nums.length
2 <= n <= 10^5
0 <= nums[i] <= 10^9
解法1——二分答案
class Solution {public int minimizeArrayValue(int[] nums) {int l = Integer.MAX_VALUE, r = Integer.MIN_VALUE;for (int x: nums) {l = Math.min(l, x);r = Math.max(r, x);}while (l < r) {int mid = l + r >> 1;if (check(mid, nums)) r = mid;else l = mid + 1;}return l;}public boolean check(int k, int[] nums) {if (nums[0] > k) return false;long d = k - nums[0]; // 使用long防止溢出for (int i = 1; i < nums.length; ++i) {if (nums[i] <= k) d += k - nums[i];else {d -= nums[i] - k;if (d < 0) return false;}}return true;}
}
解法2——分类讨论O(n)
首先最大值的最小值是 nums[0]。
对于 nums[1],当其 < nums[0] 时,答案还是 nums[0];当其 > nums[0] 时,则答案是两者的平均向上取整。
class Solution {public int minimizeArrayValue(int[] nums) {long mx = 0, sum = 0;for (int i = 0; i < nums.length; ++i) {sum += nums[i];// (sum + i) / (i + 1) 是因为要向上取整mx = Math.max(mx, (sum + i) / (i + 1)); }return (int)mx;}
}
2513. 最小化两个数组中的最大值(二分答案+lcm+容斥原理)🐂好题!
https://leetcode.cn/problems/minimize-the-maximum-of-two-arrays/
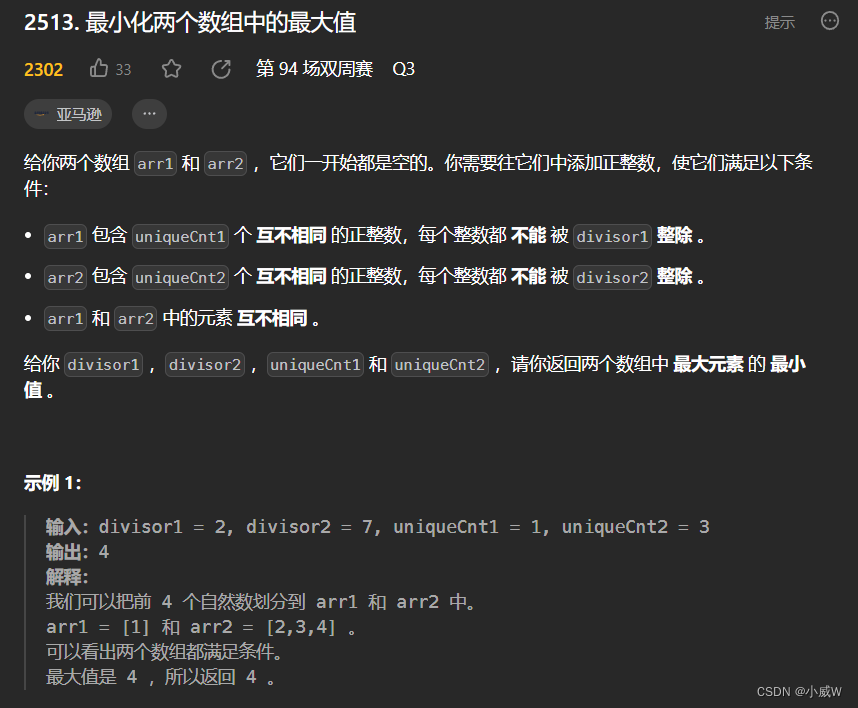
提示:
2 <= divisor1, divisor2 <= 10^5
1 <= uniqueCnt1, uniqueCnt2 < 10^9
2 <= uniqueCnt1 + uniqueCnt2 <= 10^9
二分答案。
class Solution {public int minimizeSet(int divisor1, int divisor2, int uniqueCnt1, int uniqueCnt2) {long l = 0, r = (long)Integer.MAX_VALUE;while (l < r) {long mid = l + r >> 1;// 两个数组不能选择的数字数量long x = mid / divisor1, y = mid / divisor2, z = mid / lcm(divisor1, divisor2);long sum = uniqueCnt1 + uniqueCnt2 + z; // 至少需要的数字数量// arr1不能使用的,看arr2能不能使用;反之同理sum += Math.max(0, x - z - uniqueCnt2) + Math.max(0, y - z - uniqueCnt1);if (sum <= mid) r = mid;else l = mid + 1;}return (int)l;}// 最小公倍数public long lcm(long x, long y) {return x / gcd(x, y) * y;}// 最大公因数public long gcd(long x, long y) {return y == 0? x: gcd(y, x % y);}
}
相似题目(容斥原理+二分查找)
878. 第 N 个神奇数字
https://leetcode.cn/problems/nth-magical-number/
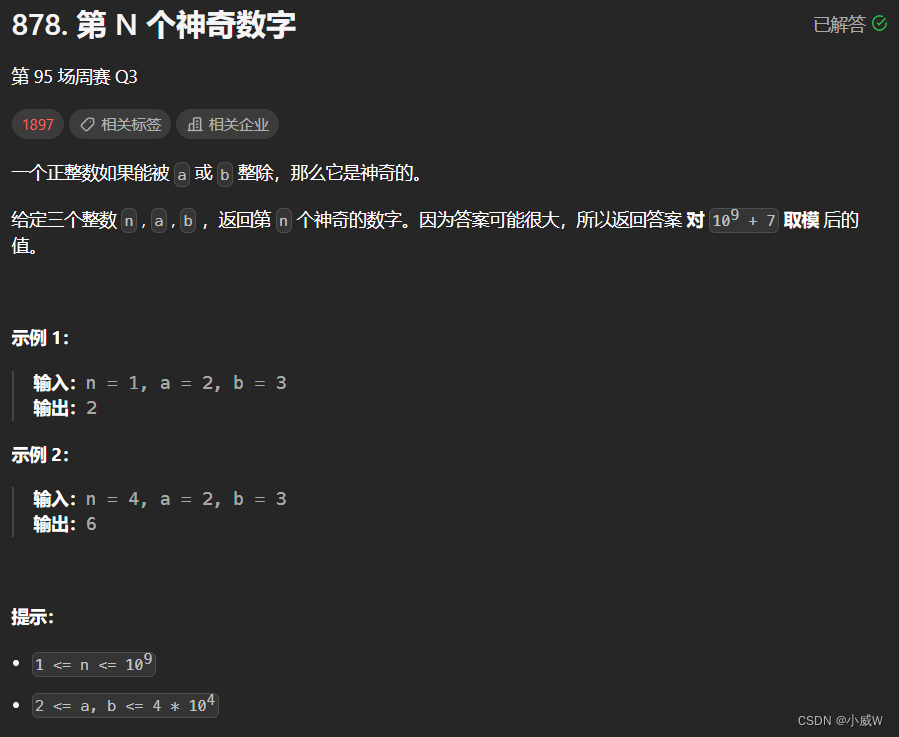
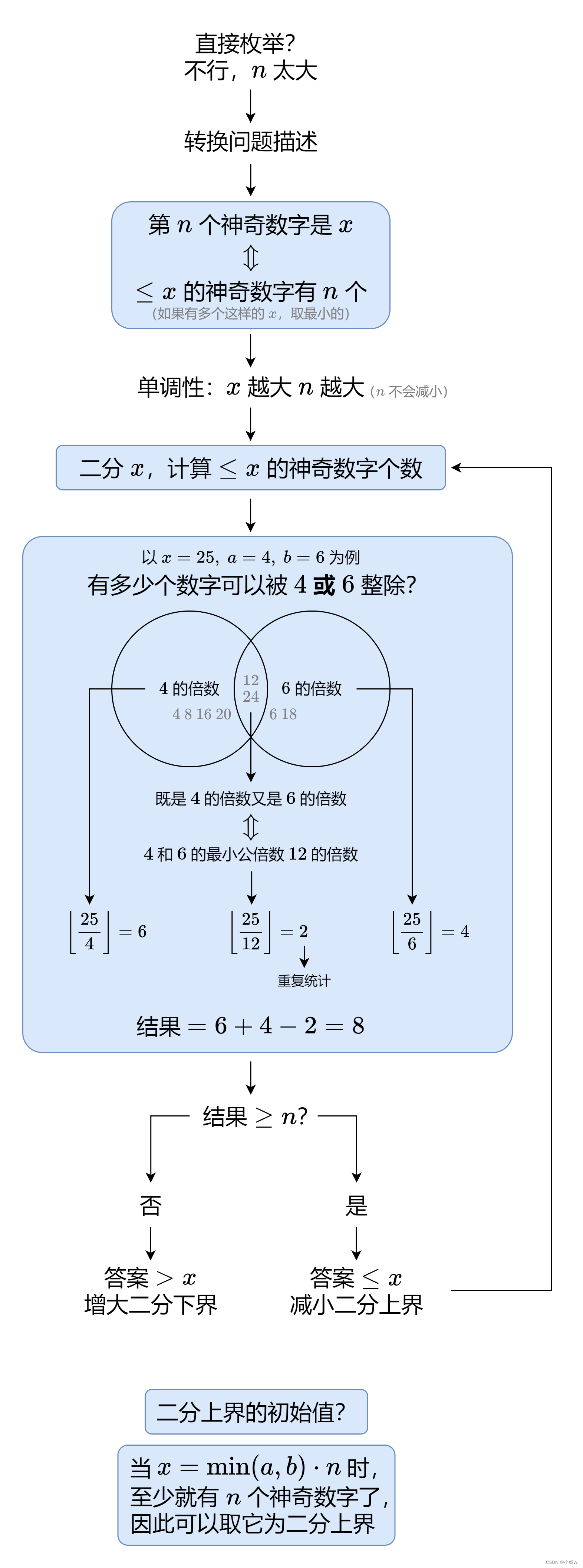
答案可能会很大,所以先将变量设置成 long 类型。
class Solution {final long MOD = (long)1e9 + 7;public int nthMagicalNumber(int n, int a, int b) {long c = lcm(a, b);long l = 2, r = Long.MAX_VALUE - 2;while (l < r) {long mid = l + r >> 1;long x = mid / a, y = mid / b, z = mid / c;long s = x + y - z; // 容斥原理if (s < n) l = mid + 1;else r = mid;}return (int)(l % MOD);}public long lcm(long a, long b) {return a * b / gcd(a, b);}public long gcd(long a, long b) {return b == 0? a: gcd(b, a % b);}
}
1201. 丑数 III
https://leetcode.cn/problems/ugly-number-iii/description/
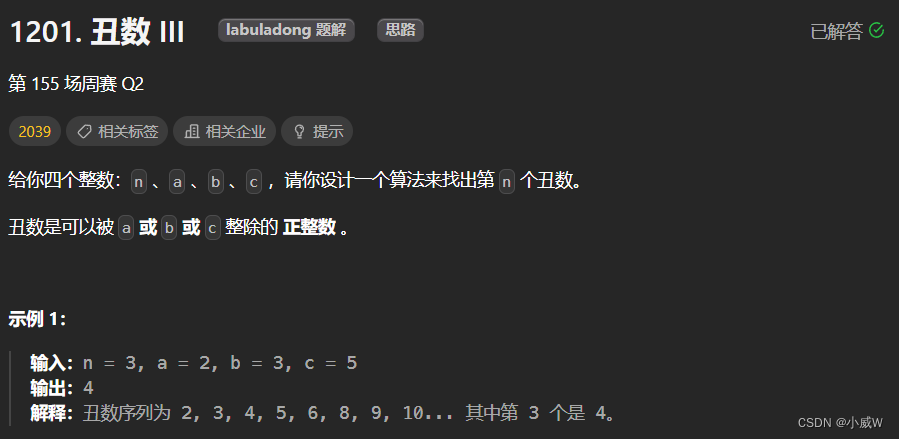
提示:
1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
本题结果在 [1, 2 * 10^9] 的范围内
注意这题也要先使用 long 数据类型。
class Solution {public int nthUglyNumber(int n, int a, int b, int c) {// 注意要转成longlong x = lcm(a, b), y = lcm(b, c), z = lcm(a, c), q = lcm(x, y);long l = 1, r = (long)2e9;while (l < r) {long mid = l + r >> 1;long aa = mid / a, bb = mid / b, cc = mid / c, xx = mid / x, yy = mid / y, zz = mid / z, qq = mid / q;// 容斥原理long s = aa + bb + cc - xx - yy - zz + qq;if (s < n) l = mid + 1;else r = mid;}return (int)l;}// 求最小公倍数public long lcm(long a, long b) {return a / gcd(a, b) * b;}// 求最大公因数public long gcd(long a, long b) {return b == 0? a: gcd(b, a % b);}
}
2517. 礼盒的最大甜蜜度(二分答案)
https://leetcode.cn/problems/maximum-tastiness-of-candy-basket/
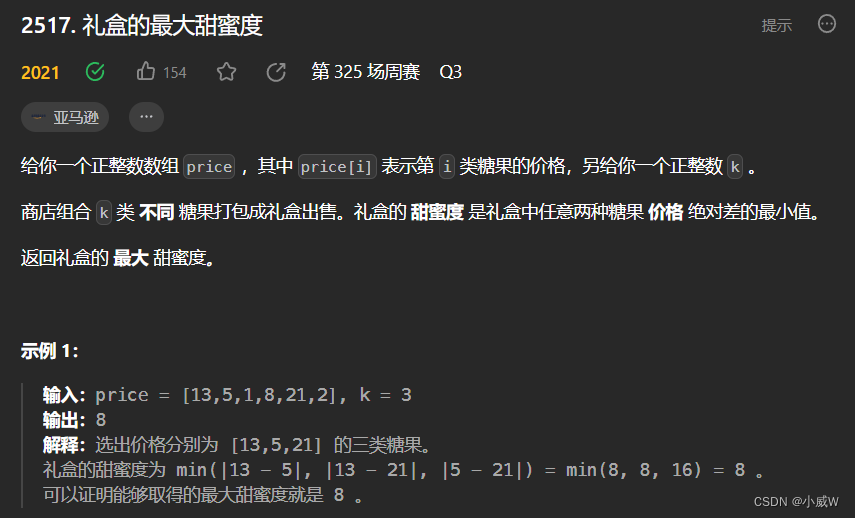
提示:
2 <= k <= price.length <= 10^5
1 <= price[i] <= 10^9
class Solution {public int maximumTastiness(int[] price, int k) {Arrays.sort(price);int n = price.length, l = 0, r = price[n - 1] - price[0];while (l < r) {int mid = l + r + 1 >> 1;int s = 1, last = price[0];for (int i = 1; i < n && s < k; ++i) {if (price[i] - last >= mid) {s++;last = price[i];}}if (s < k) r = mid - 1;else l = mid;}return l;}
}
相关文章:

【算法】二分答案
文章目录 相关链接什么时候使用二分答案?题目列表最大化最小化相关题目列表📕2439. 最小化数组中的最大值解法1——二分答案解法2——分类讨论O(n) 2513. 最小化两个数组中的最大值(二分答案lcm容斥原理)🐂好题&#x…...

阿曼市场最全开发攻略,看这一篇就够了
中东是一个充满外贸机遇的市场,已经成为很多外贸人重点开发的市场。 阿曼的海岸南方和东方临阿拉伯海,东北方则抵阿曼湾。阿曼因为扼守着世界上最重要的石油输出通道——波斯湾和阿曼湾之间的霍尔木兹海峡,所以地理位置非常重要,…...

探讨UUID和Secrets:确保唯一性与数据安全的利器
😀前言 在现代软件开发中,唯一标识符(UUID)和机密信息的处理是至关重要的。UUID是用于唯一标识数据记录和对象的128位值,确保了全球范围内的唯一性。同时,Python的secrets模块为处理机密信息提供了强大的随…...

06-Redis缓存高可用集群
上一篇:05-Redis高可用集群之水平扩展 1.集群方案比较 哨兵模式 在redis3.0以前的版本要实现集群一般是借助哨兵sentinel工具来监控master节点的状态,如果master节点异常,则会做主从切换,将某一台slave作为master,…...

LCP 18.早餐组合
题目来源: leetcode题目,网址:LCP 18. 早餐组合 - 力扣(LeetCode) 解题思路: 按序遍历饮料数组,二分查找符合要求 staple 中满足要求的最大值所在位置。最后返回所有*(最大位置…...

Tomcat调优【精简版】
Tomcat调优 优化Tomcat内存分配 调整Tomcat启动脚本contalina.sh,设置tomcat启动时分配的内存很可使用的最大内存; CATALINA_OPTS 调整Tomcat线程池 Tomcat默认使用的线程池:ThreadPoolExecutor 可以通过修改server.xml的 Connector 节点下的 maxThreads、minSpareThread…...

通过NDK编译C程序运行在iMX6q开发板上
在之前想要在Ubuntu系统中编译c语言程序为可执行文件并放在装有Android6.0.1系统的imx6q开发板上运行,采用gcc编译器进行编译的时候,虽然可以生成可执行文件但是却出现了错误,最终采用手段仍然无法在板子上运行,但是转换思路后&am…...
【学习笔记】Java 一对一培训(2.1)Java基础语法
【学习笔记】Java 一对一培训(2.1)Java基础语法 关键词:Java、Spring Boot、Idea、数据库、一对一、培训、教学本文主要内容含Java简介、Java基础语法、Java对象和类、Java基本数据类型、Java变量类型、Java修饰符计划2小时完成,…...

外贸独立站哪家好?推荐的独立站建站平台?
如何选外贸独立站搭建系统?创建贸易网站的工具有哪些? 在如今全球贸易不断蓬勃发展的背景下,外贸独立站成为许多企业拓展国际市场的首选之一。然而,要想在竞争激烈的市场中脱颖而出,选择一家合适的外贸独立站服务提供…...
六、变量与常量
变量与常量 1.变量与常量1.1标识符和关键字1.1.1.标识符1.1.2.关键字 1.2.声明变量1.3.声明常量1.4.变量的有效范围1.4.1.成员变量1.4.2.局部变量 1.5.训练11.6.训练2 —————————————————————————————————————————————————— …...

Fork() 函数:“父” 与 “子” 进程的交互(进程的创建)
阅读导航 前言一、fork函数初识1. 基本概念2. fork函数返回值 二、fork函数的写时拷贝三、总结温馨提示 前言 前面我们讲了C语言的基础知识,也了解了一些数据结构,并且讲了有关C的一些知识,也学习了一些Linux的基本操作,也了解并…...

JupyterNotebook设置Python环境的方法步骤
不多说,看链接。 https://stackoverflow.com/questions/39604271/conda-environments-not-showing-up-in-jupyter-notebook conda activate myenv pip install ipykernel python -m ipykernel install --user --name myenv --display-name "Python (myenv)&q…...
腾讯云阿里云云服务器 Linux 操作系统 BT 宝塔面板快速建站教程
宝塔面板概述 宝塔面板是一款服务器管理软件,支持Windows和Linux系统,可以通过Web端轻松管理服务器,提升运维效率。总体来说,宝塔面板具有操作简单、功能丰富、安全可靠等特点,是一款非常实用的服务器管理软件。 宝塔…...

【Linux】死锁理解
什么是死锁 因为资源调度的方式不合理或者资源的稀缺性,导致进程间的相互等待。 死锁的四个必要条件:互斥条件,请求和保持条件,环路等待条件,不可剥夺条件。 死锁的预防只要破坏死锁产生的四个必要条件。通常采用预…...

基于Java所涉及的人工智能的框架
11 References: [1] Java中人工智能的框架_永远的12的博客-CSDN博客...

【力扣】三角形最小路径和
目录 题目 例子 示例 1: 示例 2: 前言 思路 思想 代码 调用的函数 主函数 所有代码 力扣提交的代码 运行结果 小结 题目 给定一个三角形 triangle ,找出自顶向下的最小路径和。 每一步只能移动到下一行中相邻的结点上。相邻的结…...
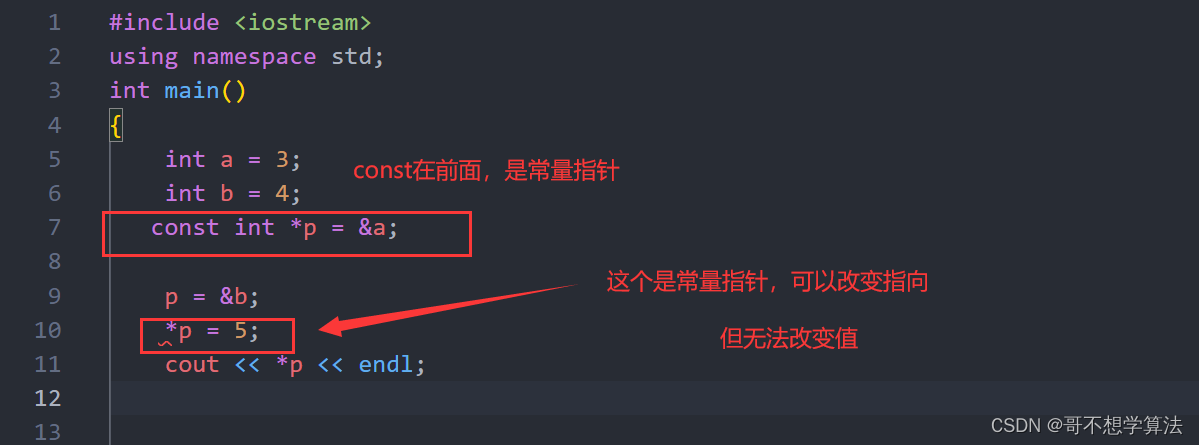
【Linux】指针常量和常量指针
这个是指针常量,不能修改指向【其实就是引用的原型】:可以理解为const是否限制了星号 这个是常量指针,可以改指向,不能改值:...

LCP 22.黑白方格画
题目来源: leetcode题目,网址:LCP 22. 黑白方格画 - 力扣(LeetCode) 解题思路: 分别计算当涂0行,1行,2行.......时能否满足要求,若能ÿ…...
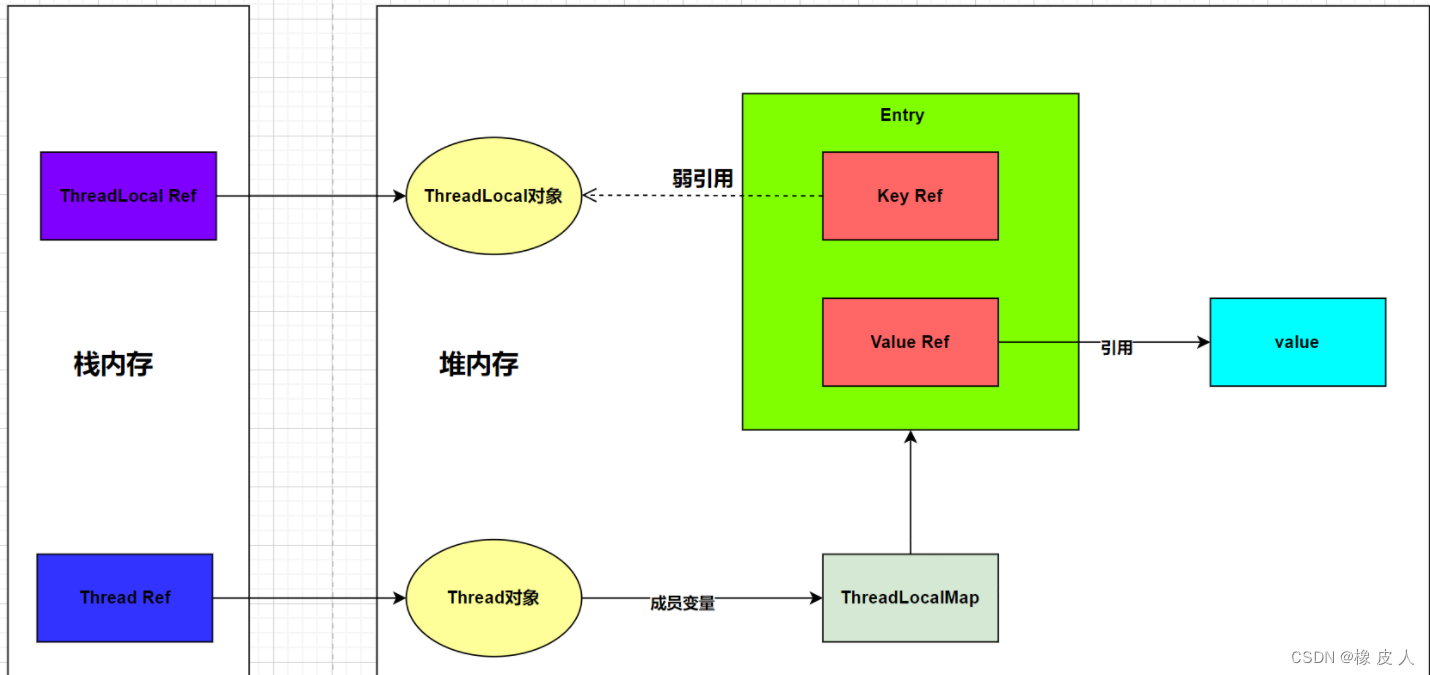
Java并发编程第8讲——ThreadLocal详解
ThreadLocal无论是在项目开发还是面试中都会经常碰到,它的重要性可见一斑,本篇文章就从ThreadLocal的使用、实现原理、核心方法的源码、内存泄漏问题等展开介绍一下。 一、什么是ThreadLocal ThreadLocal是java.lang下面的一个类,在JDK 1.2版…...
保研记录)
2023复旦大学计算机科学技术(网络空间安全)保研记录
BG:中九rank前5%、科研经历少、无竞赛 复旦大学计算机科学与技术--网络空间安全方向,参营4天(6.26-6.29),管午饭,住宿自理 6.26--报道听会,6.27--听会+实验室参观 给了…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
