当前位置： 首页 > news >正文

等差数列和等比数列 常用公式

news 2026/2/10 7:34:36

等差数列

定义

a_{n+1}-a_{n}=d

通项公式

a_{n}=a_{1}+\left ( n-1 \right )d，

a_{n}=a_{m}+(n-m)d

公差

d=\frac{a_{n}-a_{1}}{n-1}\left ( n\neq 1 \right )，

d=\frac{a_{n}-a_{m}}{n-m}(n\neq m)

前n项和公式

S_{n}=\frac{n(a_{1}+a_{n})}{2}=na_{1}+\frac{n(n-1)}{2}d

中项公式

A=\frac{a+b}{2}

下标：m+n=p+q，则

a_{m}+a_{n}=a_{p}+a_{q}

等比数列

定义

\frac{a_{n+1}}{a_{n}}=q

通项公式

a_{n}=a_{1}q^{n-1}，

a_{n}=a_{m}q^{n-m}

公比

q^{n-1}=\frac{a_{n}}{a_{1}}，

q^{n-m}=\frac{a_{n}}{a_{m}}

前n项和公式

S_{n}=\frac{a_{1}(1-q^{n})}{1-q}=\frac{a_{1}-a_{n}q}{1-q}(q\neq 1)，

S_{n}=na_{1}(q=1)

中项公式

G=\pm \sqrt{ab}(ab>0)

下标：m+n=p+q，则

a_{m}a_{n}=a_{p}a_{q}

相关文章：

等差数列和等比数列 常用公式

等差数列 定义 通项公式 ， 公差 ， 前n项和公式 中项公式 下标：mnpq，则 等比数列 定义 通项公式 ， 公比 ， 前n项和公式 ， 中项公式 下标：mnpq，则...

编程日记 2023/9/22 18:23:07

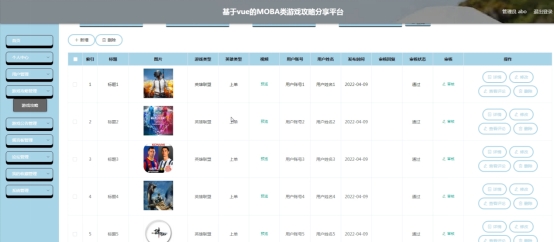
基于SpringBoot+Vue的MOBA类游戏攻略分享平台

1 简介 MOBA类游戏攻略分享平台，为用户随时随地查看游戏攻略信息提供了便捷的方法，更重要的是大大的简化了管理员管理MOBA类游戏攻略信息的方式方法，更提供了其他想要了解MOBA类游戏攻略信息及运作情况以及挑选方便快捷的可靠渠道。相比于传…...

编程日记 2023/9/22 18:20:05

基于异常上线场景的实时拦截与问题分发策略

作者 | 彭阳 导读 性能中台负责MEG端研发数据的接入、传输、管理、应用等各个环节。为了应对移动应用领域中端技术的快速迭代和线上突增问题的挑战，中台提出了实时拦截与问题的分发机制，旨在在端上线的不同阶段及时发现并拦截异常上线，最大程…...

编程日记 2023/9/22 18:19:03

MySQL常见面试题（一）

😀前言 在数据库管理系统中，存储引擎起着核心的角色，它决定了数据管理和存储的方式。MySQL作为一个领先的开源关系型数据库管理系统，提供了多种存储引擎来满足不同的需求和优化不同的应用。除了选择合适的存储引擎，数据…...

编程日记 2023/9/22 18:18:02

webpack：详解entry和output一些重要API的使用

文章目录 contextentry单个入口多个入口entry相关API例一例二例三 outputoutput.assetModuleFilenameoutput.chunkFilenameoutput.clean【5.20.0版本支持】output.filename【重要】output.globalObjectoutput.library【重要】output.library.nameoutput.library.type【重要】ou…...

编程日记 2023/9/22 18:15:00

Spring后处理器-BeanPostProcessor

Spring后处理器-BeanPostProcessor Bean被实例化后，到最终缓存到名为singletonObjects单例池之前，中间会经过bean的初始化过程（（该后处理器的执行时机）），例如：属性的填充、初始化方…...

编程日记 2023/9/22 18:10:55

每日一题~修剪二叉树

原题链接：669. 修剪二叉搜索树 - 力扣（LeetCode） 题目描述： 思路分析： 由题可知，我们要将原来的二叉搜索树调整为值在 low~high 之间的新二叉搜索树，接下来我们分析一下针对不同的节点的处理方…...

编程日记 2023/9/22 18:08:53

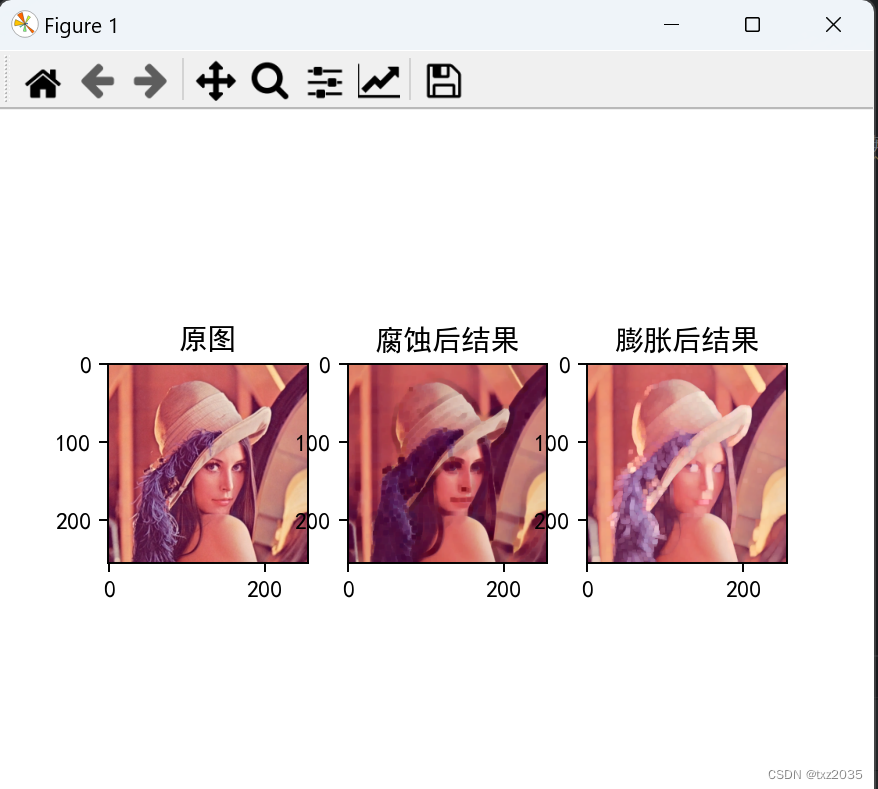
图像形态学操作（连通性、腐蚀、膨胀）

相关概念 形态学操作-腐蚀 参数： img: 要处理的图像kernal :核结构iteration ：腐蚀的次数，默认是1 形态学操作-膨胀 参数： img : 要处理的图像kernal : 核结构iteration : 膨胀的次数，默认为1 import cv2 as cv im…...

编程日记 2023/9/22 18:07:52

中国这么多 Java 开发者，应该诞生出生态级应用开发框架

1、必须要有，不然就永远不会有 应用开发框架，虽然没有芯片、操作系统、数据库、编程语言这些重要。但是最终呈现在用户面前的，总是有软件部分。而软件系统开发，一般都需要应用开发框架，它是软件系统的基础性部件之一。…...

编程日记 2023/9/22 18:06:51

仿猫扑盒子引流神器试看神马视频-红包打卡签到领金

特点1：站内发红包，抢红包 特点2：会员可上传视频 特点3：设置每天免费试看次数…..具体看演示站点，为准 支付在后台上传收款二维码即可，支持微信和支付宝。前台提交订单后台管理员审核 环境：宝…...

编程日记 2023/9/22 18:05:51

WhatsApp自动营销软件是真实的吗？对做外贸有帮助吗？

出海营销少不了的就是依靠海外平台，WhatsApp作为许多海外国家和地区最受欢迎的聊天应用程序，活跃用户占到了全球人口的四分之一，有些地区比如欧洲、美洲，用户渗透率超过了80%，对海外营销的企业来说是不可缺少的销售工具…...

编程日记 2023/9/22 18:00:46

抖音短视频矩阵系统搭建

企业在进行短视频矩阵运营时，搭建一个矩阵号是非常必要的。矩阵号可以绑定多个不同平台的账号，批量制作和定时发布短视频，提高企业的曝光量和粉丝互动。但是，如何搭建一个有效的短视频矩阵号呢？以下是几个关键步骤。 一…...

编程日记 2023/9/22 17:58:44

Chinese-LLaMA-AIpaca

文章目录 关于 Chinese-LLaMA-Alpaca一、LLaMA模型 --> HF格式二、合并LoRA权重，生成全量模型权重方式1：单LoRA权重合并方式2：多LoRA权重合并（适用于Chinese-Alpaca-Plus ）三、使用 Transformers 进行推理四、使用 webui 搭建界面1、克隆text-generation-webui并安装必…...

编程日记 2023/9/22 17:57:43

IP归属地应用的几个主要特点

作为一款优秀的IP地址定位工具，主题IP归属地的应用无疑是最好的选择之一。该应用可以将您需要查询的IP地址快速定位到所在的具体物理位置，并提供详细的地址和地图信息。接下来，让我们一起来看一看IP归属地应用的几个主要特点： 1. …...

编程日记 2023/9/22 17:56:41

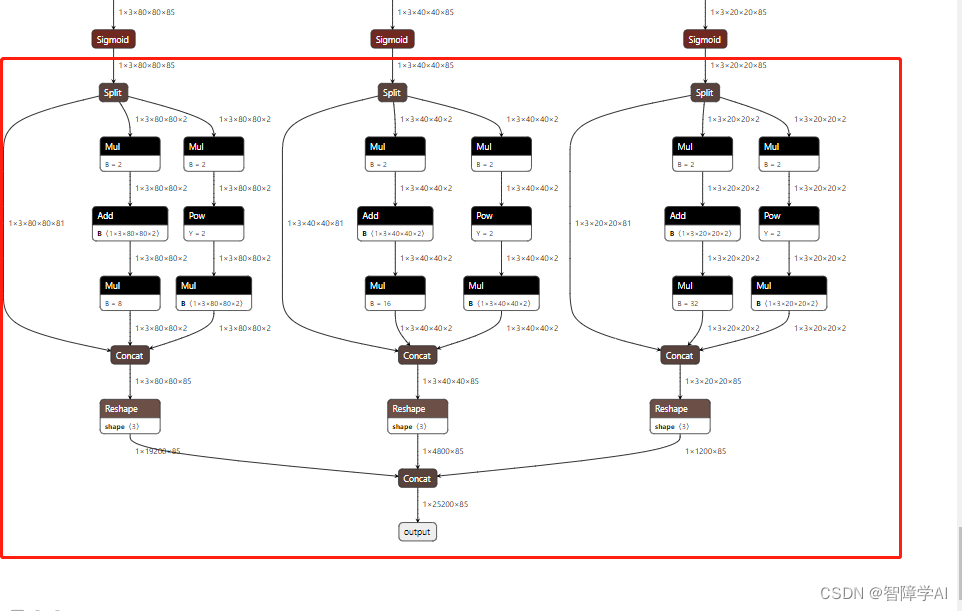
通过解读yolov5_gpu_optimization学习如何使用onnx_surgon

onnx实战一: 解析yolov5 gpu的onnx优化案例: 这是一个英伟达的仓库, 这个仓库的做法就是通过用gs对onnx进行修改减少算子然后最后使用TensorRT插件实现算子， 左边是优化过的, 右边是原版的。 通过这个案例理解原版的onnx的导出流程然后我们看英伟达是怎么拿gs来优化…...

编程日记 2023/9/22 17:55:41

图像复原与重建，解决噪声的几种空间域复原方法（数字图像处理概念 P4）

文章目录 图像复原模型噪声模型只存在噪声的空间域复原 图像复原模型 噪声模型 只存在噪声的空间域复原...

编程日记 2023/9/22 17:54:40

Android 启动优化案例：WebView非预期初始化排查

去年年底做启动优化时，有个比较好玩的 case 给大家分享下，希望大家能从我的分享里 get 到我在做一些问题排查修复时是怎么看上去又low又土又高效的。 1. 现象 在我们使用 Perfetto 进行app 启动过程性能观测时，在 UI 线程发现了一段 几十毫…...

编程日记 2023/9/22 17:53:39

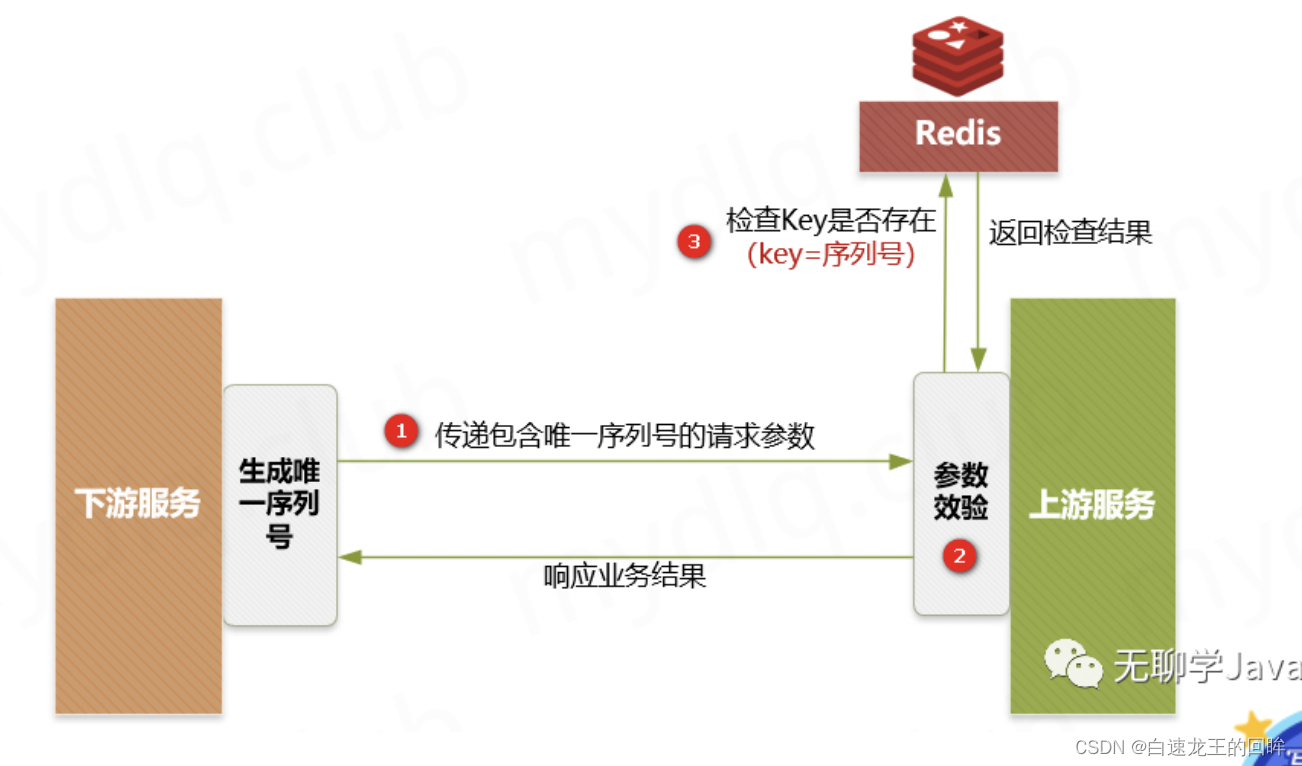
20230919后台面经整理

1.你认为什么是操作系统，操作系统有哪些功能 os是：管理资源、向用户提供服务、硬件机器的扩展 1.进程线程管理：状态、控制、通信等 2.存储管理：分配回收、地址转换 3.文件管理：目录、操作、磁盘、存取 4.设备管理&…...

编程日记 2023/9/22 17:52:38

画一个时钟（html+css+js）

这是一个很简约的时钟。。。。。。。 效果&#xff1a; 代码&#xff1a; <template><div class"demo-box"><div class"clock"><ul class"mark"><liv-for"(rotate, index) in rotatedAngles":key"i…...

编程日记 2023/9/22 17:49:35

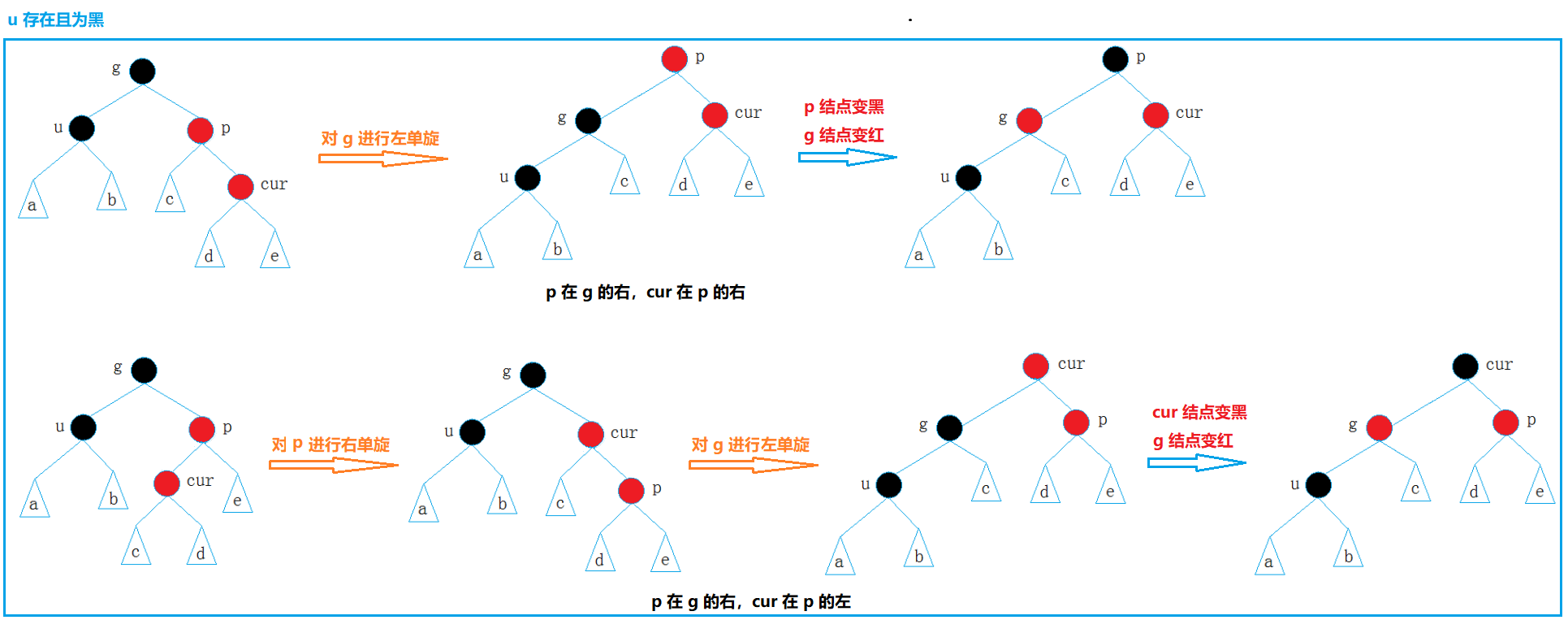
红 黑 树

文章目录 一、红黑树的概念二、红黑树的实现1. 红黑树的存储结构2. 红黑树的插入 一、红黑树的概念 在 AVL 树中删除一个结点&#xff0c;旋转可能要持续到根结点&#xff0c;此时效率较低 红黑树也是一种二叉搜索树&#xff0c;通过在每个结点中增加一个位置来存储红色或黑色…...

编程日记 2023/9/22 17:46:32

深度学习在微纳光子学中的应用

深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向&#xff1a; 逆向设计 通过神经网络快速预测微纳结构的光学响应&#xff0c;替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

编程新知 2026/2/10 7:11:42

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例

文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...

编程新知 2026/2/9 1:38:05

对WWDC 2025 Keynote 内容的预测

借助我们以往对苹果公司发展路径的深入研究经验&#xff0c;以及大语言模型的分析能力&#xff0c;我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际&#xff0c;我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测&#xff0c;聊作存档。等到明…...

编程新知 2026/2/6 23:56:39

相机从app启动流程

一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下： 重点代码分析： 启动相机前，先要通过getCameraIdList获取camera的个数以及id，然后可以通过getCameraCharacteristics获取对应id camera的capabilities（静态信息）进行一些openCamera前的…...

编程新知 2026/1/31 5:09:19

Linux云原生安全：零信任架构与机密计算

Linux云原生安全&#xff1a;零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言&#xff1a;云原生安全的范式革命 随着云原生技术的普及&#xff0c;安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测&#xff0c;到2025年&#xff0c;零信任架构将成为超…...

编程新知 2025/8/17 17:11:47

相机Camera日志分析之三十一：高通Camx HAL十种流程基础分析关键字汇总（后续持续更新中）

【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了：有对最普通的场景进行各个日志注释讲解，但相机场景太多，日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志，通过下列分类关键字搜索，即可清晰的分析不同场景的相机运行流程差异…...

编程新知 2025/11/20 7:13:43

深入解析C++中的extern关键字：跨文件共享变量与函数的终极指南

&#x1f680; C extern 关键字深度解析&#xff1a;跨文件编程的终极指南 &#x1f4c5; 更新时间&#xff1a;2025年6月5日 &#x1f3f7;️ 标签&#xff1a;C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言&#x1f525;一、extern 是什么&#xff1f;&…...

编程新知 2026/2/1 6:50:07

学习STC51单片机32（芯片为STC89C52RCRC）OLED显示屏2

每日一言 今天的每一份坚持&#xff0c;都是在为未来积攒底气。 案例&#xff1a;OLED显示一个A 这边观察到一个点&#xff0c;怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 &#xff1a; 如果代码里信号切换太快&#xff08;比如 SDA 刚变&#xff0c;SCL 立刻变&#…...

编程新知 2026/2/6 0:50:24

企业如何增强终端安全？

在数字化转型加速的今天&#xff0c;企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机&#xff0c;到工厂里的物联网设备、智能传感器&#xff0c;这些终端构成了企业与外部世界连接的 “神经末梢”。然而&#xff0c;随着远程办公的常态化和设备接入的爆炸式…...

编程新知 2026/1/29 9:14:58

基于matlab策略迭代和值迭代法的动态规划

经典的基于策略迭代和值迭代法的动态规划matlab代码&#xff0c;实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

编程新知 2025/12/7 23:28:25