DSU ON TREE
DSU ON TREE
DSU:并查集
DSU ON TREE:树上启发式合并
我也不知道为啥树上并查集就是树上启发式合并
启发式合并的思想是每次把小的往大的合并,也就是最大化利用已有的答案(大的数组不用清空,在原基础上加上小的即可)。转移到树上,“大”显然就是树的重心。
能解决什么样的问题?需要统计子树信息,但是子树的信息不好合并。比如权值是否出现(桶)。所以肯定要留下最大的,也就是树链剖分的重儿子。
考虑两种合并方式(以对子树做桶排序为例,保留重儿子数组):
- 遍历子树的桶,对应相加,即类似num[x][val]+=num[v][val],复杂度O(值域)
- 遍历子树,直接num[x][val[v]]++,复杂度O(子树大小)
显然第一种太大了。
同时,显然不能对每个节点开一个桶表示“以x为根的子树的桶”,空间无法接受,所以桶只能留到一维,这就涉及到清空,因为在dfs另一个儿子时前一个子树的影响要清空。所以要尽可能少的减少清空,在dfs时如果最后访问重儿子,那就可以不清空最大的一部分。
void dfs2(int x,int fa,int save)
{for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa || v==mxson[x]) continue;dfs2(v,x,0);}if (mxson[x]) dfs2(mxson[x],x,1);if (!show[dis[x]]) show[dis[x]]=deep[x];else show[dis[x]]=min(show[dis[x]],deep[x]);int need=k+2*dis[x]-dis[x];if (show.count(need)){int mndep=show[need];int nowans=mndep+deep[x]-2*deep[x]; ans=min(ans,nowans);}for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa || v==mxson[x]) continue;calc_ans(v,x,x),add(v,x);}//if (!save) del(x,fa);if (!save) show.clear();
}
大致这个样子,save表示是否要清空桶。先跑轻儿子,清空桶。再跑重儿子,不清空桶,那么这个桶里的东西再回溯到父亲节点时依然保留。同时注意为什么先calc_ans再add,是为了避免有两个点在同一棵子树内的情况,即 u → l c a → x → l c a → v u\rightarrow lca\rightarrow x\rightarrow lca\rightarrow v u→lca→x→lca→v的情况。在题目里往往这种情况不合法。
例题
洛谷P4149 [IOI2011] Race
题目链接
题目大意:给一棵树,每条边有权。求一条简单路径,权值和等于k,且边的数量最小。
思路:问题转化为选择点对 ( u , v ) (u,v) (u,v),满足 d i s u + d i s v − d i s l c a ( u , v ) = k dis_u+dis_v-dis_{lca(u,v)}=k disu+disv−dislca(u,v)=k,最小化 d e e p u + d e e p v − d e e p l c a ( u , v ) deep_u+deep_v-deep_{lca(u,v)} deepu+deepv−deeplca(u,v),考虑处理以 x x x为根的子树的答案,不妨设 l c a ( u , v ) = x lca(u,v)=x lca(u,v)=x,在dfs到点u时,只需要查找 k + 2 ∗ d i s x − d i s u k+2*dis_x-dis_u k+2∗disx−disu的点,都可以作为点 v v v(移项可得),此时考虑需要最小化的值, d e e p u deep_u deepu和 d e e p x deep_x deepx都是已知值,所以只需要开一个桶(map)维护 m a p [ d ] map[d] map[d]表示 d i s = d dis=d dis=d的点的 d e e p deep deep最小值。
解决了思路,剩下的就是实现DSU ON TREE。注意先遍历子树求解,再将该子树加入桶。
#include<bits/stdc++.h>
#define pa pair<int,int>
#define INF 0x3f3f3f3f
#define inf 0x3f
#define fi first
#define se second
#define mp make_pair
#define ll long long
#define ull unsigned long long
#define pb push_backusing namespace std;inline ll read()
{ll f=1,sum=0;char c=getchar();while (!isdigit(c)) {if (c=='-') f=-1;c=getchar();}while (isdigit(c)) {sum=sum*10+c-'0';c=getchar();}return sum*f;
}
const int MAXN=200010;
struct edge{int next,to,val;
}e[MAXN*2];
int head[MAXN],cnt;
void addedge(int u,int v,int w)
{e[++cnt].next=head[u];e[cnt].to=v;e[cnt].val=w;head[u]=cnt;
}
int sz[MAXN],mxson[MAXN],mxsz[MAXN];
int deep[MAXN],ans,k;
ll dis[MAXN];
void dfs1(int x,int fa)
{sz[x]=1;for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa) continue;dis[v]=dis[x]+e[i].val;deep[v]=deep[x]+1;dfs1(v,x);sz[x]+=sz[v];if (sz[v]>mxsz[x]) mxson[x]=v,mxsz[x]=sz[v];}
}
map <ll,int> show;
void del(int x,int fa)
{show[dis[x]]=0;for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa) continue;del(v,x);}
}
void add(int x,int fa)
{if (!show.count(dis[x])) show[dis[x]]=deep[x];else show[dis[x]]=min(show[dis[x]],deep[x]);for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa) continue;add(v,x);}
}
void calc_ans(int x,int fa,int rt)
{int need=k+2*dis[rt]-dis[x];if (show.count(need)){int mndep=show[need];int nowans=mndep+deep[x]-2*deep[rt];ans=min(ans,nowans);}for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa) continue;calc_ans(v,x,rt);}
}
void dfs2(int x,int fa,int save)
{for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa || v==mxson[x]) continue;dfs2(v,x,0);}if (mxson[x]) dfs2(mxson[x],x,1);if (!show[dis[x]]) show[dis[x]]=deep[x];else show[dis[x]]=min(show[dis[x]],deep[x]);int need=k+2*dis[x]-dis[x];if (show.count(need)){int mndep=show[need];int nowans=mndep+deep[x]-2*deep[x]; ans=min(ans,nowans);}for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa || v==mxson[x]) continue;calc_ans(v,x,x),add(v,x);}//if (!save) del(x,fa);if (!save) show.clear();
}
int main()
{int n=read(); k=read();for (int i=1;i<n;i++){int u=read()+1,v=read()+1,w=read();addedge(u,v,w);addedge(v,u,w);}deep[1]=1;dfs1(1,0);//for (int i=1;i<=n;i++) cout<<deep[i]<<' '<<dis[i]<<' '<<mxson[i]<<endl;ans=INF;dfs2(1,0,0);if (ans==INF) cout<<-1<<endl;else cout<<ans<<endl;return 0;
}
有一个小细节是要单独计算一下根的答案,因为在后面的过程中并没有再次进入重儿子,所以会漏掉重儿子到子树树根的这种答案。其他情况都已经在后面的不断加入中包含。
例题
CF 600E Lomsat gelral
题目链接
题目大意:一棵树每个点有个颜色,求以每个点为根的子树出现最多的颜色的编号之和。
思路:朴素的DSU ON TREE,开个桶记录就行,众数用set维护,当出现更大的,清空set,出现相等的,插入set即可。
#include<bits/stdc++.h>
#define pa pair<int,int>
#define INF 0x3f3f3f3f
#define inf 0x3f
#define fi first
#define se second
#define mp make_pair
#define ll long long
#define ull unsigned long long
#define pb push_backusing namespace std;inline ll read()
{ll f=1,sum=0;char c=getchar();while (!isdigit(c)) {if (c=='-') f=-1;c=getchar();}while (isdigit(c)) {sum=sum*10+c-'0';c=getchar();}return sum*f;
}
const int MAXN=100010;
struct edge{int next,to;
}e[MAXN*2];
int head[MAXN],cnt;
void addedge(int u,int v)
{e[++cnt].next=head[u];e[cnt].to=v;head[u]=cnt;
}
int sz[MAXN],mxson[MAXN],mxsz[MAXN];
void pre_dfs(int x,int fa)
{for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa) continue;pre_dfs(v,x);sz[x]+=sz[v];if (sz[v]>mxsz[x]) mxson[x]=v,mxsz[x]=sz[v];}sz[x]++;
}
set <int> s;
int num[MAXN],nowmax,col[MAXN];
ll nowsum;
void del(int x,int fa)
{num[col[x]]--;for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa) continue;del(v,x);}
}
void add(int x,int fa)
{num[col[x]]++;if (num[col[x]]>nowmax){nowmax++;s.clear();s.insert(col[x]);nowsum=col[x];}else if (num[col[x]]==nowmax){nowsum+=col[x];s.insert(col[x]);}for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa) continue;add(v,x);}
}
ll ans[MAXN];
void dfs(int x,int fa,int save)
{for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa || v==mxson[x]) continue;dfs(v,x,0);}if (mxson[x]) dfs(mxson[x],x,1);num[col[x]]++;if (num[col[x]]>nowmax){nowmax++;s.clear();s.insert(col[x]);nowsum=col[x];}else if (num[col[x]]==nowmax){nowsum+=col[x];s.insert(col[x]);}for (int i=head[x];i;i=e[i].next){int v=e[i].to;if (v==fa || v==mxson[x]) continue;add(v,x);}ans[x]=nowsum;if (!save) del(x,fa),nowsum=0,s.clear(),nowmax=0;
}
int main()
{int n=read();for (int i=1;i<=n;i++) col[i]=read();for (int i=1;i<n;i++){int u=read(),v=read();addedge(u,v),addedge(v,u);}pre_dfs(1,0);dfs(1,0,0);for (int i=1;i<=n;i++) cout<<ans[i]<<' ';cout<<endl;return 0;
}
相关文章:

DSU ON TREE
DSU ON TREE DSU:并查集 DSU ON TREE:树上启发式合并 我也不知道为啥树上并查集就是树上启发式合并 启发式合并的思想是每次把小的往大的合并,也就是最大化利用已有的答案(大的数组不用清空,在原基础上加上小的即可&…...

Java“对象”
Java:PO、VO、BO、DO、DAO、DTO、POJO PO持久化对象(Persistent Object) PO是持久化对象,用于表示数据库中的实体或表的映射通常与数据库表的结构和字段对应PO的属性对应数据库表的字段,可以进行持久化操作࿰…...

vuepress+gitee免费搭建个人在线博客(无保留版)
文章目录 最终效果,一睹为快!一、工具选型二、什么是VuePress三、准备工作3.1 node 安装3.2 Git安装3.3 Gitee账号注册 四、搭建步骤4.1 初始化VuePress4.2 安装VuePress4.3 初始化目录4.4 编写文章 五、部署到Gitee5.1 创建仓库5.2 个人空间地址设置4.3…...

Android 12.0 系统限制上网系列之iptables用IOemNetd实现app上网白名单的功能实现
1.前言 在12.0的系统rom定制化开发中,对于系统限制网络的使用,在system中netd网络这块的产品需要中,会要求设置app上网白名单的功能, liunx中iptables命令也是比较重要的,接下来就来在IOemNetd这块实现app上网白名单的的相关功能,就是在 系统中只能允许某个app上网,就是…...

Idea和DataGrip自定义常用代码模板,熟练使用快捷模板可促进开发效率
场景: 在实际工作中,我们不可能一个一个字母的去敲代码,为了提升开发效率,可以使用常用的快捷代码模板。idea和datagrip自带的有,我们也可以自定义快捷模板 一、Idea自定义代码模板、有些是基于 hutool 常用包 1、-&g…...

Vue.js :实现嵌套对话框的查看按钮
Vue.js :实现嵌套对话框的查看按钮 Vue.js 是一款流行的 JavaScript 框架,用于构建交互性强、响应式的前端应用程序。本博客将介绍如何使用 Vue.js 和 Element UI 库创建一个前端应用,其中包括了嵌套对话框的查看按钮,以及如何在…...

9.2.4 【MySQL】段的结构
段不对应表空间中某一个连续的物理区域,而是一个逻辑上的概念,由若干个零散的页面以及一些完整的区组成。像每个区都有对应的XDES Entry来记录这个区中的属性一样,定义了一个INODE Entry结构来记录段中的属性。 它的各个部分释义如下…...
怎么快速提取图片中的文字信息?怎么使用OCR图片文字提取一键提取文字
图片里的文字如何提取?一些图片中的文字信息是我们需要的,但是一个个输入太麻烦了,怎么将图片上的文字提取出来?Initiator是一款易于使用的小型 macOS OCR(光学字符识别)应用程序,可提取和识别 Mac 计算机屏幕上的任…...

Selenium隐藏浏览器特征
Selenium隐藏浏览器特征 Selenium特征1. CDP2. stealth.min.js3. undetected_chromedriver4. 操作已开启的浏览器4. 常见的隐藏Selenium特征的方法4.1 修改navigator.webdriver标志4.2 改变user-agent4.3 排除或关闭一些Selenium相关的开关4.4 代码展示4.5 总结 Selenium特征 …...

Linux下的buff/cache
目录 一、buff/cache二、buff/cache与内存管理三、buff/cache对系统性能的影响四、优化buff/cache1、调整vm.dirty_ratio和vm.dirty_background_ratio2、配置vm.swappiness3、配置vm.vfs_cache_pressure 五、释放buff/cache 一、buff/cache 按照Linux内核文档所说的࿰…...
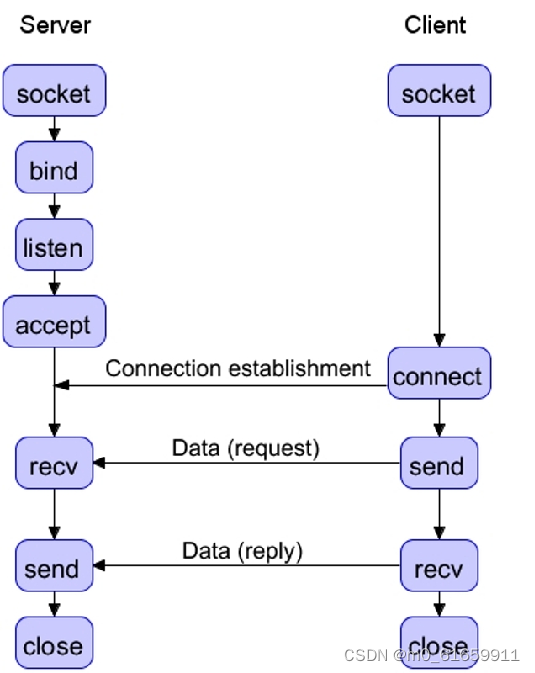
3.wifi开发,网络编程
网络协议栈LwIP WiFi UDP Clinet编程 WiFi UDP Server编程 WiFi TCP Client编程 WiFi TCP Server编程 一。LWIP原理介绍,API介绍,文件结构 1.Lwip支持的协议 2.API 3.文件结构 1.api目录:应用程序接口文件。 2.arch目录:与硬件和…...

Android框架mqtt库无法兼容高版本android13的问题
最近使用mqtt库,测试的时候发现在Android12及以下正常,但在13上闪退,闪退日志如下 java.lang.IllegalArgumentException: com.yummo.xcar: Targeting S (version 31 and above) requires that one of FLAG_IMMUTABLE or FLAG_MUTABLE be spe…...
一招解除csdn复制限制
先看这个代码 python读取英文pdf翻译成中文pdf文件导出代码 想要复制代码,csdn有限制怎么办(csdn流氓,无耻) 解除方法 ctrlu 看效果...

安全基础 --- nodejs沙箱逃逸
nodejs沙箱逃逸 沙箱绕过原理:沙箱内部找到一个沙箱外部的对象,借助这个对象内的属性即可获得沙箱外的函数,进而绕过沙箱 前提:使用vm模块,实现沙箱逃逸环境。(vm模式是nodejs中内置的模块,是no…...

Redis集群架构搭建——主从、哨兵、集群
上一篇文章Ubuntu上通过源码方式安装Redis已经介绍了如何安装redis,在这篇文章中,将会教大家搭建Redis的几种高可用的架构:主从架构、哨兵集群、Cluster集群。 本篇文章使用的redis版本为6.2.13,不同版本的配置可能有略微的区别&a…...
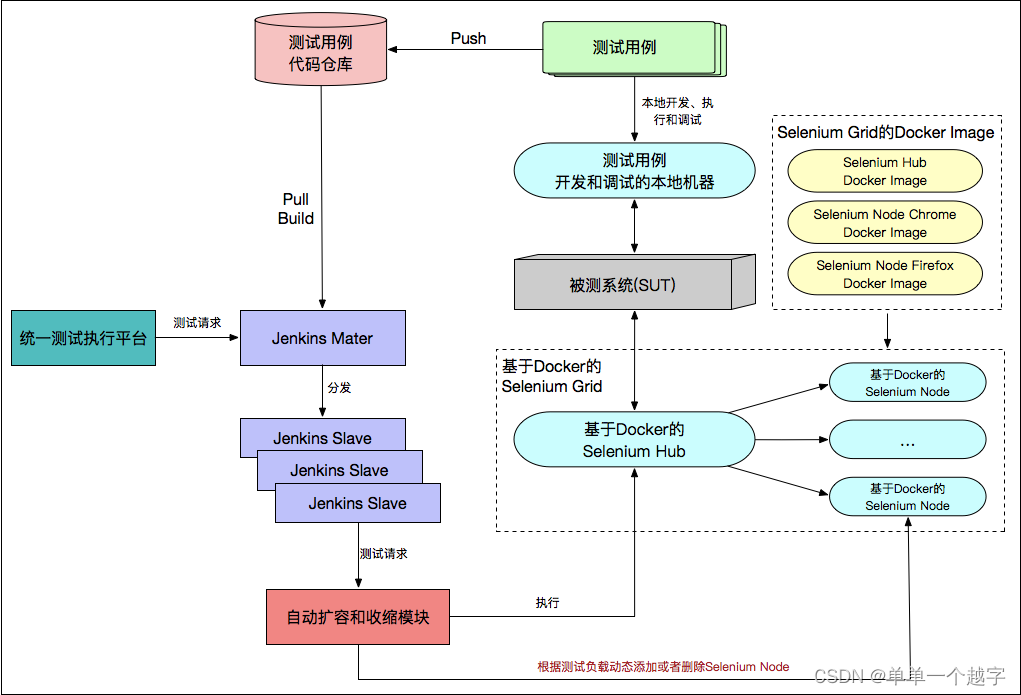
39 | selenium基础架构,UI测试架构
什么是测试基础架构? 测试基础架构指的是,执行测试的过程中用到的所有基础硬件设施以及相关的软件设施。因此,我们也把测试基础架构称之为广义的测试执行环境。通常来讲,测试基础架构主要包括以下内容: 执行测试的机器…...

2023研究生数学建模E题保姆级思路 出血性脑卒中临床智能诊疗
本次E题是一道J机器学习题目,难度也比较高,该题一般是有正确结果的,容易踩坑,不太建议小白选择,小白可以选择D题,D题思路也可以看另一篇文章,总的难度都不算低,这三道的难度接近&…...
画电路板通用知识
快捷键 快捷键 功能 shift+鼠标滚轮左右移动Ctrl+鼠标滚轮放大缩小 (Alt+) 鼠标滚轮上下移动滚轮按下鼠标滚轮可任意方向拖动图纸(可以一直保持按下状态或者按一下松开) CTRL+鼠标左键拖动复制该元件CTRL+E编辑选中元件的属性CTRL+鼠标左键 元叠选izoom in,聚焦光标所…...
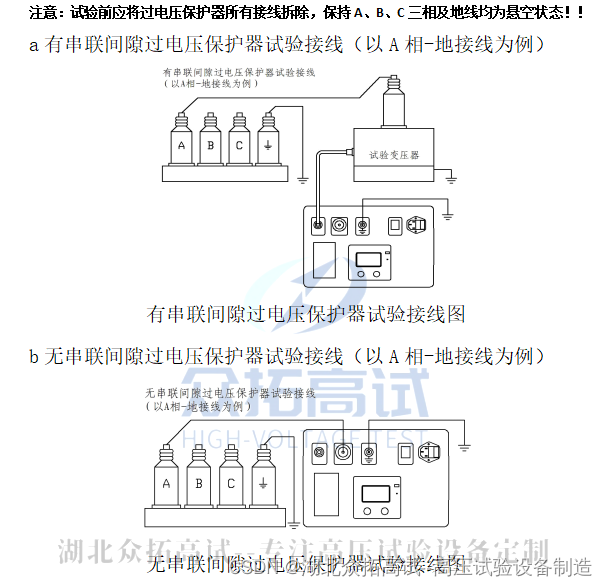
三相组合式过电压保护器试验
三相组合式过电压保护器试验 试验目的 三相组合式过电压保护器主要分为有带串联间隙过压保护器和无间隙过压保护器两大类,其试验项目内容要求分别使用高压工频交流和高压直流电源。 三相组合式过电压保护器试验,主要是为了及早发现设备内部绝缘受潮及…...

C++提高编程:01 模板
这里写目录标题 1 模板的概念2 函数模板2.1 函数模板语法2.2 函数模板注意事项2.3 函数模板案例2.4 普通函数与函数模板的区别2.5 普通函数与函数模板的调用规则2.6 模板的局限性 3 类模板3.1 类模板语法3.2 类模板与函数模板区别3.3 类模板中成员函数创建时机3.4 类模板对象做…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
