剑指 Offer 55 - I. 二叉树的深度
摘要
剑指 Offer 55 - I. 二叉树的深度
一、深度优先搜索
如果我们知道了左子树和右子树的最大深度l和r,那么该二叉树的最大深度即为:max(l,r)+1。
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言,在计算当前二叉树的最大深度时,可以先递归计算出其左子树和右子树的最大深度,然后在 O(1)O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;} else {int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return Math.max(leftHeight, rightHeight) + 1;}}
}复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 为二叉树节点的个数。每个节点在递归中只被遍历一次。
- 空间复杂度:O(height)O(height),其中 heightheight 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
二、广度优先搜索
我们也可以用广度优先搜索的方法来解决这道题目,但我们需要对其进行一些修改,此时我们广度优先搜索的队列里存放的是当前层的所有节点。每次拓展下一层的时候,不同于广度优先搜索的每次只从队列里拿出一个节点,我们需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即我们是一层一层地进行拓展,最后我们用一个变量 ans来维护拓展的次数,该二叉树的最大深度即为 ans。
public int maxDepth2(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<TreeNode>();// 加入root节点queue.offer(root);int ans = 0;while (!queue.isEmpty()) {int size = queue.size();while (size > 0) {TreeNode node = queue.poll();if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}size--;}// 将每一层的队列的值都弹出即为深度数ans++;}return ans;}复杂度分析
- 时间复杂度:O(n),其中n为二叉树的节点个数。与方法一同样的分析,每个节点只会被访问一次。
- 空间复杂度:此方法空间的消耗取决于队列存储的元素数量,其在最坏情况下会达到O(n)。
三、平衡二叉树
判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
有了计算节点高度的函数,即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历,即对于当前遍历到的节点,首先计算左右子树的高度,如果左右子树的高度差是否不超过1,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。
package Tree;/*** @Classname JZ55平衡二叉树* @Description TODO* @Date 2023/2/23 16:51* @Created by xjl*/
public class JZ55平衡二叉树 {public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}}public boolean isBalanced(TreeNode root) {if (root == null) {return true;} else {// 要求这个左子树的和右子树都要小于这个,同时要求这个树本身的高度差不能超过1return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);}}public int height(TreeNode root) {if (root == null) {return 0;} else {// 返回的是这个树的高度return Math.max(height(root.left), height(root.right)) + 1;}}
}
复杂度分析
- 时间复杂度:O(n^2),其中n是二叉树中的节点个数。最坏情况下,二叉树是满二叉树,需要遍历二叉树中的所有节点,时间复杂度是 O(n)。对于节点p,如果它的高度是d,则height(p)最多会被调用d次(即遍历到它的每一个祖先节点时)。对于平均的情况,一棵树的高度h 满足O(h)=O(logn),因为 d≤h,所以总时间复杂度为 O(nlogn)。对于最坏的情况,二叉树形成链式结构,高度为 O(n),此时总时间复杂度为 O(n^2)
- 空间复杂度:O(n),其中 n是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数,递归调用的层数不会超过n。
博文参考
《leetcode》
相关文章:

剑指 Offer 55 - I. 二叉树的深度
摘要 剑指 Offer 55 - I. 二叉树的深度 一、深度优先搜索 如果我们知道了左子树和右子树的最大深度l和r,那么该二叉树的最大深度即为:max(l,r)1。 而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计…...
Bean的生命周期和作用域
Bean的生命周期Bean的执行流程:Bean 执行流程:启动Spring 容器 -> 实例化 Bean(分配内存空间,从无到有)-> Bean 注册到 Spring 中(存操作) -> 将 Bean 装配到需要的类中(取…...
TestNG和Junit的区别,测试框架该如何选择?
要想知道两个框架的区别,首先分别介绍一下两个框架。 TestNG是一个java中的开源自动化测试框架,其灵感来自JUnit和NUnit,TestNG还涵盖了JUnit4整个核心的功能,但引入了一些新的功能,使其功能更强大,使用更…...

MySQL安全登录策略
MySQL密码复杂度策略设置 MySQL 系统自带有 validate_password 插件,此插件可以验证密码强度,未达到规定强度的密码则不允许被设置。MySQL 5.7 及 8.0 版本默认情况下貌似都不启用该插件,这也使得我们可以随意设置密码,比如设置为…...

优化模型验证23:带无人机停靠站的卡车无人机协同配送车辆路径问题、模型、gurobipy验证及结果可视化
带中转hub的卡车无人机车辆路径问题 模型来源为:Wang Z , Sheu J B . Vehicle routing problem with drones[J]. Transportation Research Part B: Methodological, 2019, 122(APR.):350-364. 问题描述: 这篇问题研究了一个带停靠站的卡车无人机路径问题,无人机仅能从起点…...

mongoTemplate Aggregation 多表联查 排序失效问题解决
目录说明说明 接着上一个文章的例子来说:mongoTemplate支持多表联查 排序 条件筛选 分页 去重分组 在按照上一个demo的代码执行后,可能会发生排序失效的问题,为什么说可能呢?每个人负责业务不同,不可能是最简单的dem…...

什么是智慧实验室?
智慧实验室是利用现代信息技术和先进设备将实验室实现智能化和智慧化的概念。通过将各种数据、信息和资源整合在一起,实现实验室设备的互联互通,数据的实时采集、传输、处理和分析,从而提高实验室的效率、精度和可靠性。一、智慧实验室包含多…...

Python abs() 函数
Python abs() 函数Python 数字描述abs() 函数返回数字的绝对值。语法以下是 abs() 方法的语法:abs( x )参数x -- 数值表达式。返回值函数返回x(数字)的绝对值。实例以下展示了使用 abs() 方法的实例:#!/usr/bin/python print "abs(-45) …...
裸辞了,面试了几十家软件测试公司,终于找到想要的工作
上半年裁员,下半年裸辞,有不少人高呼裸辞后躺平真的好快乐!但也有很多人,裸辞后的生活五味杂陈。 面试了几十家终于找到心仪工作 因为工作压力大、领导PUA等各种原因,今年2月下旬我从一家互联网小厂裸辞,没…...
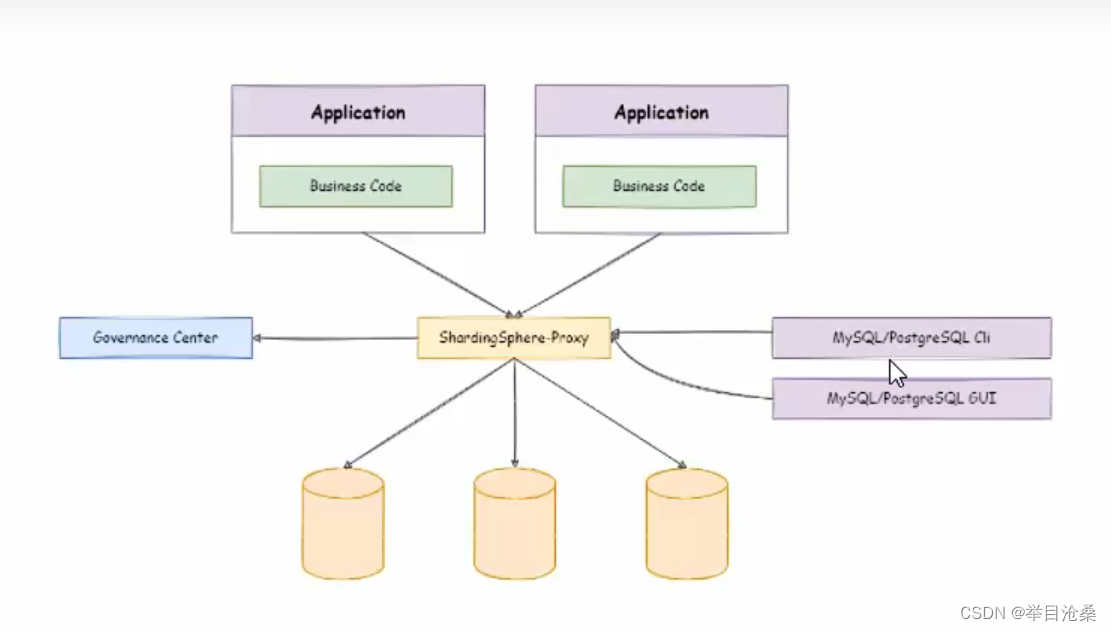
ShardingSphere
1.简介 1.开源的分布式数据生态项目 ShardingSphere-JDBC:轻量级Java框架ShardingSphere-Proxy:数据库代理ShardingSphere-Sidecar(规划中):Kubernetes的云原生数据库代理 2.使用版本:ShardingSphere5.1.1 1.数据库集群架构 1.出现…...
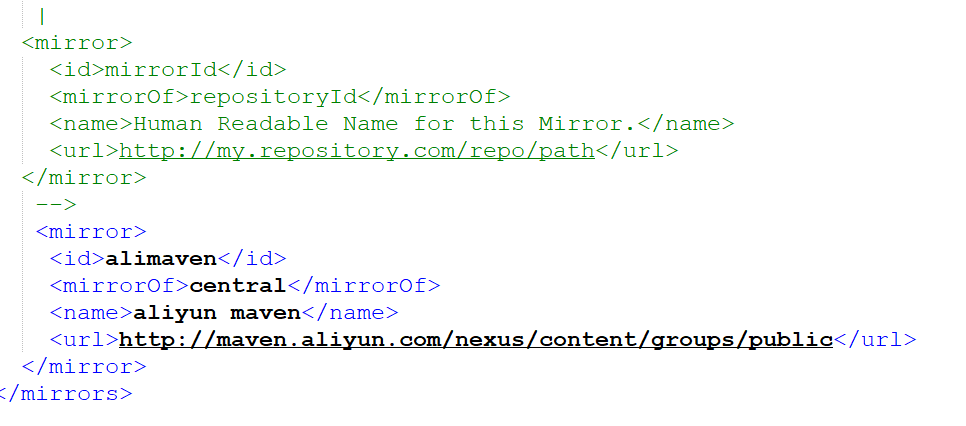
配置Maven
对于刚开始认识的Maven的初学者超级有用的哦!项目统一共享使用一套jar包,由maven统一管理。节省了jar空间,统一jar包版本首先将maven安装完毕测试有没有配置完成,在命令框里面打 mvn -version进行测试maven安装完,第一…...

赛宁网安“网络安全卓越中心”:立足科技创新 推动网安产业高质量发展
2月22日上午,网络安全卓越中心CPCOE——圆桌论坛活动在南京召开。本次论坛由南京未来科技城主办,南京赛宁信息技术有限公司承办。论坛上,江苏省科协副主席、南京理工大学教授李千目,江苏省互联网协会副理事长兼秘书长刘湘生&a…...
)
操作系统题目收录(十四)
1、 有些操作系统中将文件描述信息从目录项中分离出来,这样做的好处是()。 A:减少读文件时的I/O信息量B:减少写文件时的I/O信息量C:减少查找文件时的I/O信息量D:减少复制文件时的I/O信息量 解…...

Qt 第1课、Qt 的窗口组件和窗口类型
GUI 程序的开发原理: GUI 程序在运行的时候,操作系统会为它创造一个消息队列,消息队列用于存储操作系统发过来的系统消息。 用户使用操作系统的过程中,操作系统内核检测到用户的操作(鼠标,键盘)…...
【Jmeter】ForEach控制器
一、什么是ForEach控制器 ForEach控制器是遍历某个数组读取不同的变量值,来控制其下的采样器或控制器执行一次或多次。而这个数组可以是用户自定义变量,也可以是从前面接口请求中提取到需要的数据,然后进行遍历循环。 二、ForEach控制器相关…...

Julia 数据类型
在编程语言中,都有基本的数学运算和科学计算,它们常用的数据类型为整数和浮点数。 另外还有一个"字面量"的术语,字面量(literal)用于表达源代码中一个固定值的表示法(notation)&…...
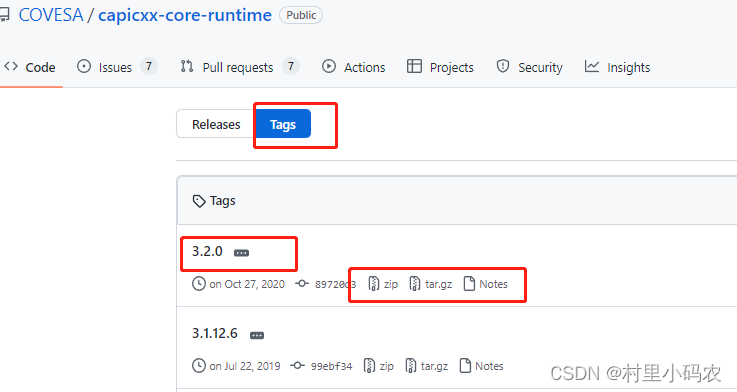
01-基于SOA架构someip 开发-Linux开发环境搭建
前言:SOME/IP 是一个汽车的中间件解决方案,可用于控制消息。从一开始,它的设计就是为了完美地适应不同尺寸和不同操作系统的设备。这包括小型设备,如相机、AUTOSAR设备,以及头部单元或远程信息处理设备。同时还确保了S…...

历时半年!从外包到现在阿里网易25K,分享一下自己的涨薪经验
前言 首先自我介绍一下,本人普通一本毕业,年初被老东家裁员干掉了,之后一直住在朋友那混吃等死,转折是今年年后,二月初的时候和大佬吃了个饭,觉得自己不能这样下去了,拿着某大佬给我的面试资料…...

支付系统中的设计模式04:改进的策略与外观模式
随着业务越做越大,交易量大了,老板觉得可以用一些变相的方法增加一些收入了,同时也有利于用户,做到双赢。这很好理解,“往地上戳一棍子都能冒出油来”,谁能扛得住这种诱惑呢? 于是,老板就提了这样的需求: 支付系统需要根据不同的结算模式,返利给账户: 1、选择T+1结算…...
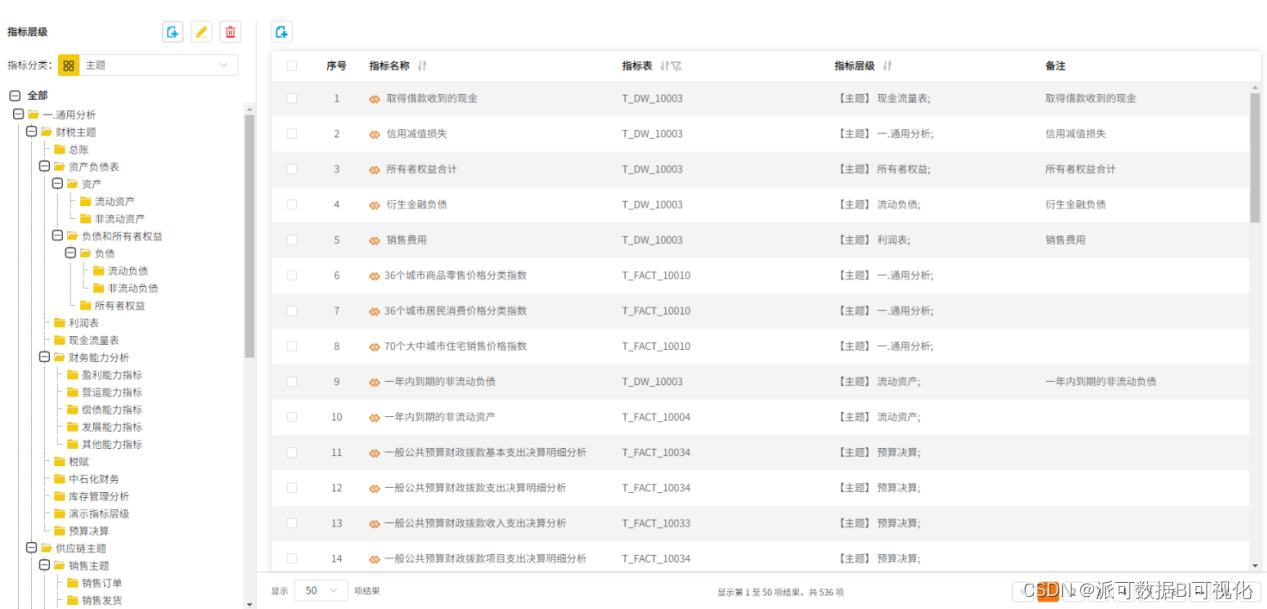
关于数据分析和数据指标,企业还需要做什么?
数据虽然已经成为了各行各业对未来的共识,也切实成为了各领域企业的重要资产。但真正谈到发挥数据的价值,就必须从规模庞大的数据中找出需求的数据,然后进行利用。这个过程光是想想就知道很麻烦,更别提很多数据都是经常会用到的&a…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...
