Gram矩阵
Gram矩阵如何计算
Gram 矩阵是由一组向量的内积构成的矩阵。如果你有一组向量 v 1 , v 2 , … , v n v_1, v_2, \ldots, v_n v1,v2,…,vn,Gram 矩阵 G G G 的元素 G i j G_{ij} Gij 就是向量 v i v_i vi 和向量 v j v_j vj 的内积。数学上,Gram 矩阵的计算方式如下:
假设有 n n n 个向量 v 1 , v 2 , … , v n v_1, v_2, \ldots, v_n v1,v2,…,vn,每个向量的维度为 m m m(这意味着每个向量都有 m m m 个元素),则 Gram 矩阵 G G G 的元素 G i j G_{ij} Gij 计算如下:
G i j = v i ⋅ v j = ∑ k = 1 m v i [ k ] ⋅ v j [ k ] G_{ij} = v_i \cdot v_j = \sum_{k=1}^{m} v_i[k] \cdot v_j[k] Gij=vi⋅vj=k=1∑mvi[k]⋅vj[k]
其中, v i [ k ] v_i[k] vi[k] 表示向量 v i v_i vi 的第 k k k 个元素, v j [ k ] v_j[k] vj[k] 表示向量 v j v_j vj 的第 k k k 个元素。
Gram 矩阵通常是一个对称矩阵,因为 G i j = G j i G_{ij} = G_{ji} Gij=Gji,这是因为内积的交换性质。Gram 矩阵在机器学习和线性代数中有广泛的应用,例如在特征提取、核方法等领域。它可以用来表示向量之间的相似性和关联。
举例
让我们通过一个具体的示例来计算一个Gram矩阵。假设有三个二维向量:
v 1 = [ 1 , 2 ] v 2 = [ 3 , 4 ] v 3 = [ 5 , 6 ] v_1 = [1, 2] v_2 = [3, 4] v_3 = [5, 6] v1=[1,2]v2=[3,4]v3=[5,6]
我们想要计算这些向量的Gram矩阵 G G G,根据前面的定义,我们计算每一对向量的内积来填充矩阵 G G G的元素。
首先,计算 G 11 G_{11} G11,即向量 v 1 v_1 v1与自己的内积:
G 11 = v 1 ⋅ v 1 = ( 1 ⋅ 1 ) + ( 2 ⋅ 2 ) = 1 + 4 = 5 G_{11} = v_1 \cdot v_1 = (1 \cdot 1) + (2 \cdot 2) = 1 + 4 = 5 G11=v1⋅v1=(1⋅1)+(2⋅2)=1+4=5
接下来,计算 G 12 G_{12} G12,即向量 v 1 v_1 v1与向量 v 2 v_2 v2的内积:
G 12 = v 1 ⋅ v 2 = ( 1 ⋅ 3 ) + ( 2 ⋅ 4 ) = 3 + 8 = 11 G_{12} = v_1 \cdot v_2 = (1 \cdot 3) + (2 \cdot 4) = 3 + 8 = 11 G12=v1⋅v2=(1⋅3)+(2⋅4)=3+8=11
继续计算 G 13 G_{13} G13, G 21 G_{21} G21, G 22 G_{22} G22, G 23 G_{23} G23, G 31 G_{31} G31, G 32 G_{32} G32,和 G 33 G_{33} G33,按照同样的方式计算每一对向量的内积。
最终,我们得到Gram矩阵 G G G如下:
G = [ 5 11 17 11 25 39 17 39 61 ] G = \begin{bmatrix} 5 & 11 & 17 \\ 11 & 25 & 39 \\ 17 & 39 & 61 \\ \end{bmatrix} G= 51117112539173961
这就是这三个向量的Gram矩阵。每个元素 G i j G_{ij} Gij表示了向量 v i v_i vi和 v j v_j vj之间的内积。这个矩阵在机器学习中可以用于许多任务,包括核方法和特征提取。
相关文章:

Gram矩阵
Gram矩阵如何计算 Gram 矩阵是由一组向量的内积构成的矩阵。如果你有一组向量 v 1 , v 2 , … , v n v_1, v_2, \ldots, v_n v1,v2,…,vn,Gram 矩阵 G G G 的元素 G i j G_{ij} Gij 就是向量 v i v_i vi 和向量 v j v_j vj 的内积。数学上&#x…...
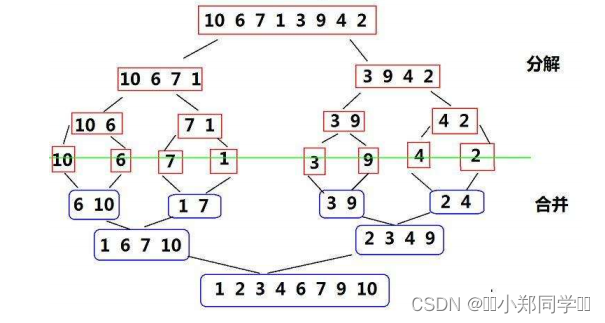
【数据结构】七大排序算法详解
目录 ♫什么是排序 ♪排序的概念 ♪排序的稳定性 ♪排序的分类 ♪常见的排序算法 ♫直接插入排序 ♪基本思想 ♪算法实现 ♪算法稳定性 ♪时间复杂度 ♪空间复杂度 ♫希尔排序 ♪基本思想 ♪算法实现 ♪算法稳定性 ♪时间复杂度 ♪空间复杂度 ♫直接选择排序 ♪基本思想 ♪算法…...

OpenCV之VideoCapture
VideoCaptrue类对视频进行读取操作以及调用摄像头。 头文件: #include <opencv2/video.hpp> 主要函数如下: 构造函数 C: VideoCapture::VideoCapture(); C: VideoCapture::VideoCapture(const string& filename); C: VideoCapture::Video…...

ESP32微控制器与open62541库: 详细指南实现OPC UA通信协议_C语言实例
1. 引言 在现代工业自动化和物联网应用中,通信协议起着至关重要的作用。OPC UA(开放平台通信统一架构)是一个开放的、跨平台的通信协议,被广泛应用于工业4.0和物联网项目中。本文将详细介绍如何在ESP32微控制器上使用C语言和open…...
怎样快速打开github.com
访问这个网站很慢是因为有DNS污染,被一些别有用心的人搞了鬼了, 可以使用火狐浏览器开启火狐浏览器的远程dns解析就可以了.我试了一下好像单独这个办法不一定有用,要结合修改hosts文件方法,双重保障 好像就可以了...

【C#】.Net基础语法二
目录 一、字符串(String) 【1.1】字符串创建和使用 【1.2】字符串其他方法 【1.3】字符串格式化的扩展方法 【1.4】字符串空值和空对象比较 【1.5】字符串中的转移字符 【1.6】大写的String和小写的string 【1.7】StringBuilder类的重要性 二、数组(Array) 【2.1】声…...

C++之this指针总结(二百二十)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

C++——如何正确的使用STL中的vector?
什么是vector? 在STL(标准模板库)中,vector是一种动态数组容器,可根据需要自动增长或缩小。它可以存储任意类型的元素,并且支持快速的随机访问。 vector是表示可变大小数组的序列容器vector采用的是连续的…...

【C语言】模拟实现内存函数
本篇文章目录 相关文章1. 模拟 memcpy 内存拷贝2. 模拟 memmove 内存移动 相关文章 【C语言】数据在内存中是以什么顺序存储的?【C语言】整数在内存中如何存储?又是如何进行计算使用的?【C语言】利用void*进行泛型编程【C语言】4.指针类型部…...

Jenkins学习笔记3
gitgithubjenkins: 架构图: 说明:jenkins知道github有更新了,就pull进行构建build,编译、自动化测试。然后部署到应用服务器。 maven java的项目构建工具。 在开发者电脑上创建空密码密钥对。 [rootgit-developer ~…...

基于单片机火灾报警器仿真设计
一、系统方案 1、本设计采用51单片机作为主控器。 2、DS18B20采集温度值送到液晶1602显示。 3、MQ2采集烟雾值,送到液晶1602显示。 4、按键设置温度报警值,大于报警值,声光报警。 二、硬件设计 原理图如下: 三、单片机软件设计…...

阿里测开面试大全(一)附答案完整版
万字长文,建议收藏 1 什么是POM,为什么要使用它? POM是Page Object Model的简称,它是一种设计思想,而不是框架。大概的意思是,把一个一个页面,当做一个对象,页面的元素和元素之间操…...

STL-常用容器
string容器 string构造函数 string本质:类 string和char*区别: char* 是一个指针 string是一个类,类内部封装了char*,管理这个字符串,是一个char*型的容器。 特点: string类内部封装了很多成员方法 …...

【owt】关闭microk8s 等无关服务
打算部署下owt,发现之前跑了microk8s ,一直运行:操作指令 // 1. 启动 microk8s.start// 2. 关闭 microk8s.stop// 3. kubectl 操作 // --- 查看 cluster microk8s.kubectl cluster-info// --- 查看 nodes microk8s.kubectl get nodes// --- 查看 pods microk8s.kubectl get …...
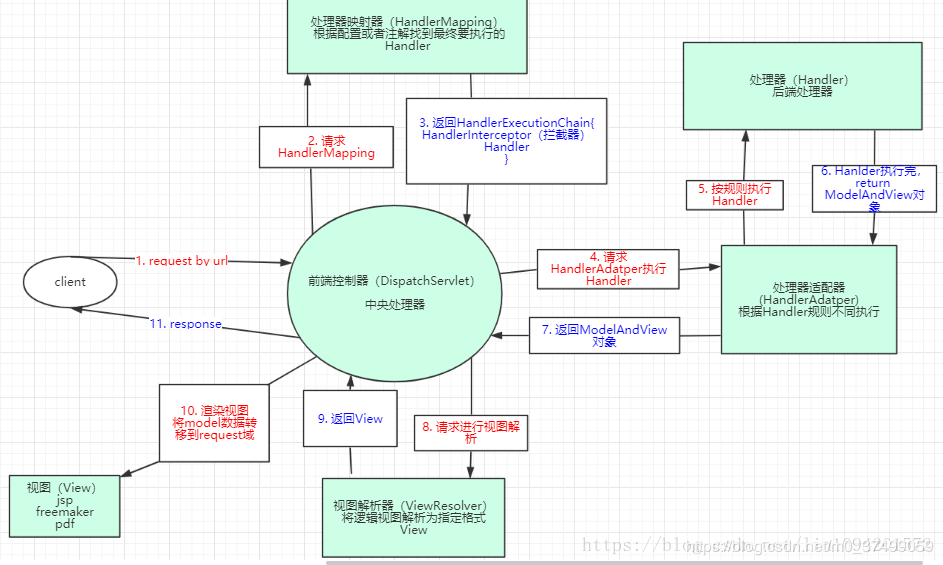
【面试题】——Spring
1.Spring是什么? Spring是一个开源的Java应用框架,它提供了广泛的基础设施支持,用于构建Java应用程序。极大提高了开发效率。它提供了一种轻量级的编程模型,通过依赖注入(Dependency Injection)和面向切面…...

【算法思想-排序】根据另一个数组次序排序 - 力扣 1122 题
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...
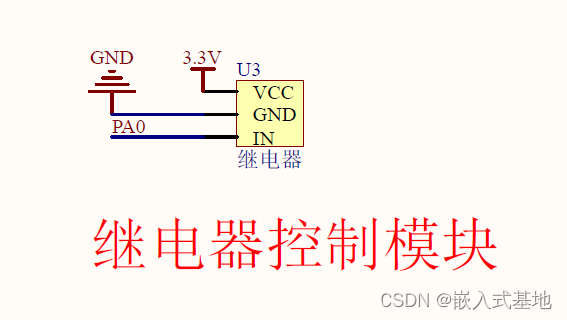
毕业设计|基于stm32单片机的app视频遥控抽水灭火小车设计
基于stm32单片机的app视频遥控抽水灭火水泵小车设计 1、项目简介1.1 系统构成1.2 系统功能 2、部分电路设计2.1 L298N电机驱动电路设计2.2 继电器控制电路设计 3、部分代码展示3.1 小车控制代码3.1 水泵控制代码 4 演示视频及代码资料获取 1、项目简介 视频简介中包含资料http…...

编译原生安卓aosp源码,实现硬改以及定位
系列文章目录 第一章 安卓aosp源码编译环境搭建 第二章 手机硬件参数介绍和校验算法 第三章 修改安卓aosp代码更改硬件参数 第四章 编译定制rom并刷机实现硬改(一) 第五章 编译定制rom并刷机实现硬改(二) 第六章 不root不magisk不xposed lsposed frida原生修改定位 第七章 安卓…...

找单身狗。一个数组中只有两个数字出现一次,其他数字出现了两次,编写一个函数找出这两个只出现一次的数字
例:在{1 2 3 4 5 6 1 2 3 4}找出5和6 方法二: 设计思想: 1.分组原理 (1)将所有数字进行异或,相同数字异或为零,所以只会剩5^6,即为异或的结果xor_result (…...

Java数据结构技巧
Java数据结构技巧 1、循环 for-each循环如果不是"[]"的数组类型,则需要提前判断数据结构是否为空,否则有可能会有空指针异常。 2、对于List对象的i到j位进行排序 for(List<String> now_result:result){List<String> sublist …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
