搜索二叉树【C++】
文章目录
- 二叉搜索树
- 二叉搜索树的模拟实现
- 构造函数
- 拷贝构造函数
- 赋值运算符重载函数
- 析构函数
- Insert
- 循环
- 递归
- Erase
- 循环
- 递归
- Find
- 循环
- 递归
- 二叉搜索树的应用
- K模型
- KV模型
- 完整代码
- 普通版本
- 递归版本
二叉搜索树
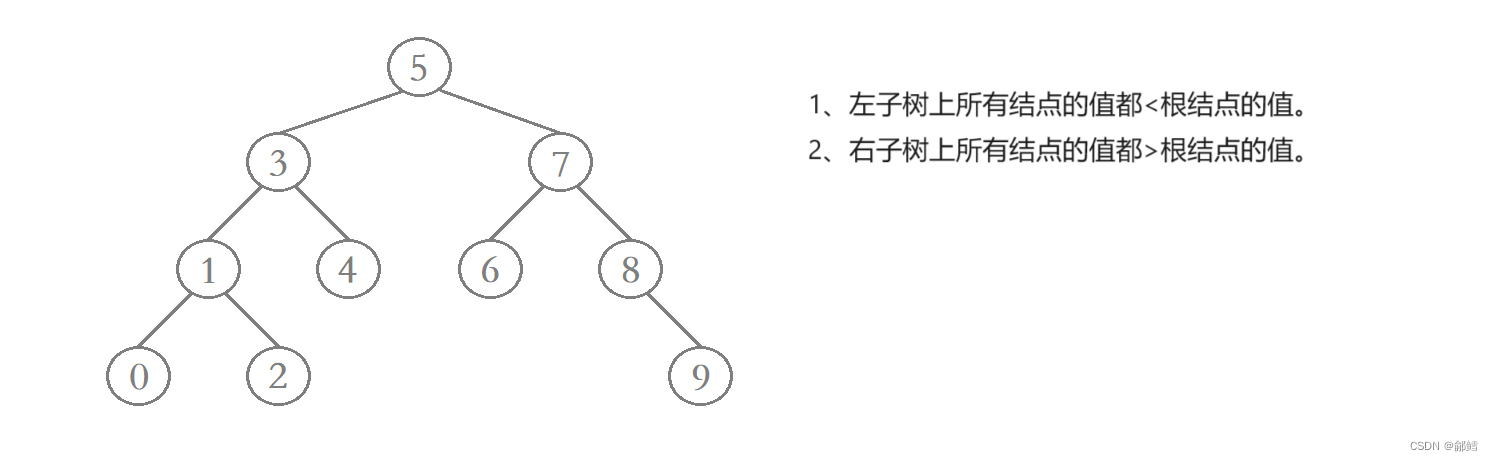
二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,
则左子树上所有结点的值都小于根结点的值。
若它的右子树不为空,
则右子树上所有结点的值都大于根结点的值。
它的左右子树也分别是二叉搜索树。
二叉搜索树的模拟实现
构造函数
BSTree():_root(nullptr){}
拷贝构造函数
BSTree(const BSTree<K>& t)//BSTree( BSTree<K> *this , const BSTree<K> & t)//t1 =t {_root = Copy(t._root);}private:Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* copyNode = new Node(root->_key);//递归 copyNode->_left = Copy(root->_left);copyNode->_right = Copy(root->_right);return copyNode;}
赋值运算符重载函数
//赋值重载 BSTree<K>& operator= (BSTree<K>& t)//t1 = t//深拷贝{swap(_root, t._root);return *this;}
析构函数
~BSTree(){Destroy(_root);}private:void Destroy(Node*& root) //引用的目的:将每个节点释放后同时置空{//后序遍历 if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}
Insert
核心思路:
如果是空树,则直接将插入结点作为二叉搜索树的根结点。
如果不是空树,则按照二叉搜索树的性质进行结点的插入。
如果待插入结点的值<根结点的值,则需要将结点插入到左子树当中。
如果待插入结点的值>根结点的值,则需要将结点插入到右子树当中。
如果待插入结点的值等于根结点的值,则插入失败。
循环
bool Insert(const K & key ){//空树if (_root == nullptr){_root = new Node(key);return true;}//不是空树Node* parent = nullptr;//找到父节点Node* cur = _root;while (cur){//比较if (cur->_key < key){//往右子树走parent = cur;cur = cur->_right;}else if (cur->_key > key){//往左子树走parent = cur;cur = cur->_left;}else{return false;}}//插入节点cur = new Node(key);//不知道parent在那一边,需要进一步判断if (parent->_key > key){//parent在左边parent->_left = cur;}else if (parent->_key < key){//parent在右边parent->_right = cur;}else{return false;}return true;}
递归
bool InsertR(const K& key)//递归版本{return _InsertR(_root, key);}private:bool _InsertR(Node*& root, const K& key) //引用的目的:不用找父节点,不需要用父节点比较大小{//结束条件if (root == nullptr){root = new Node(key);return true;}//往左子树走if (root->_key > key){return _InsertR(root->_left, key);}//往右子树走else if (root->_key < key){return _InsertR(root->_right, key);}else{return false;}}
Erase
先找到需要删除的节点
需要删除的节点可能会有三种情况:
1、待删除结点的左子树为空(待删除结点的左右子树均为空包含在内)
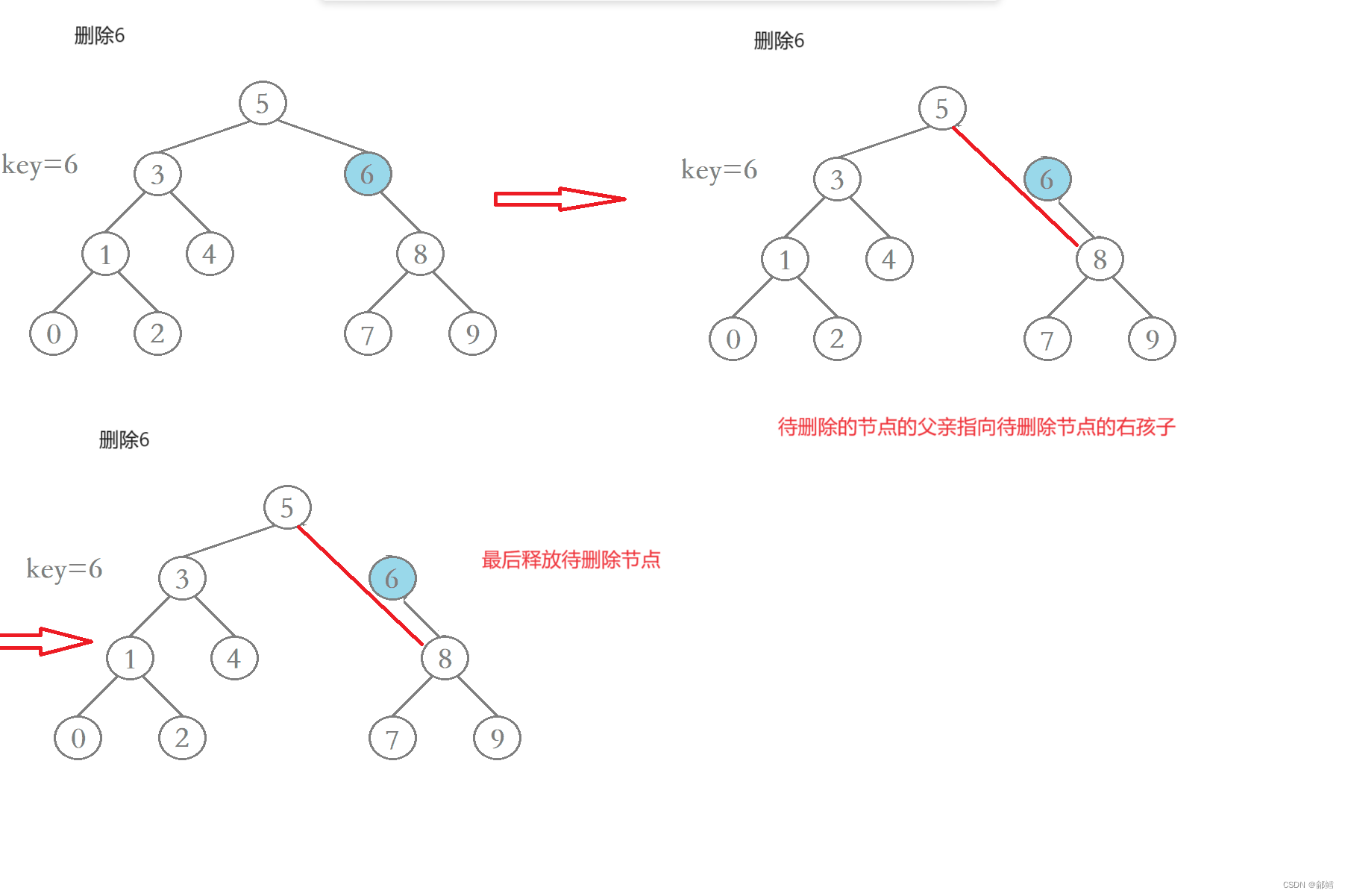
2、待删除结点的右子树为空。
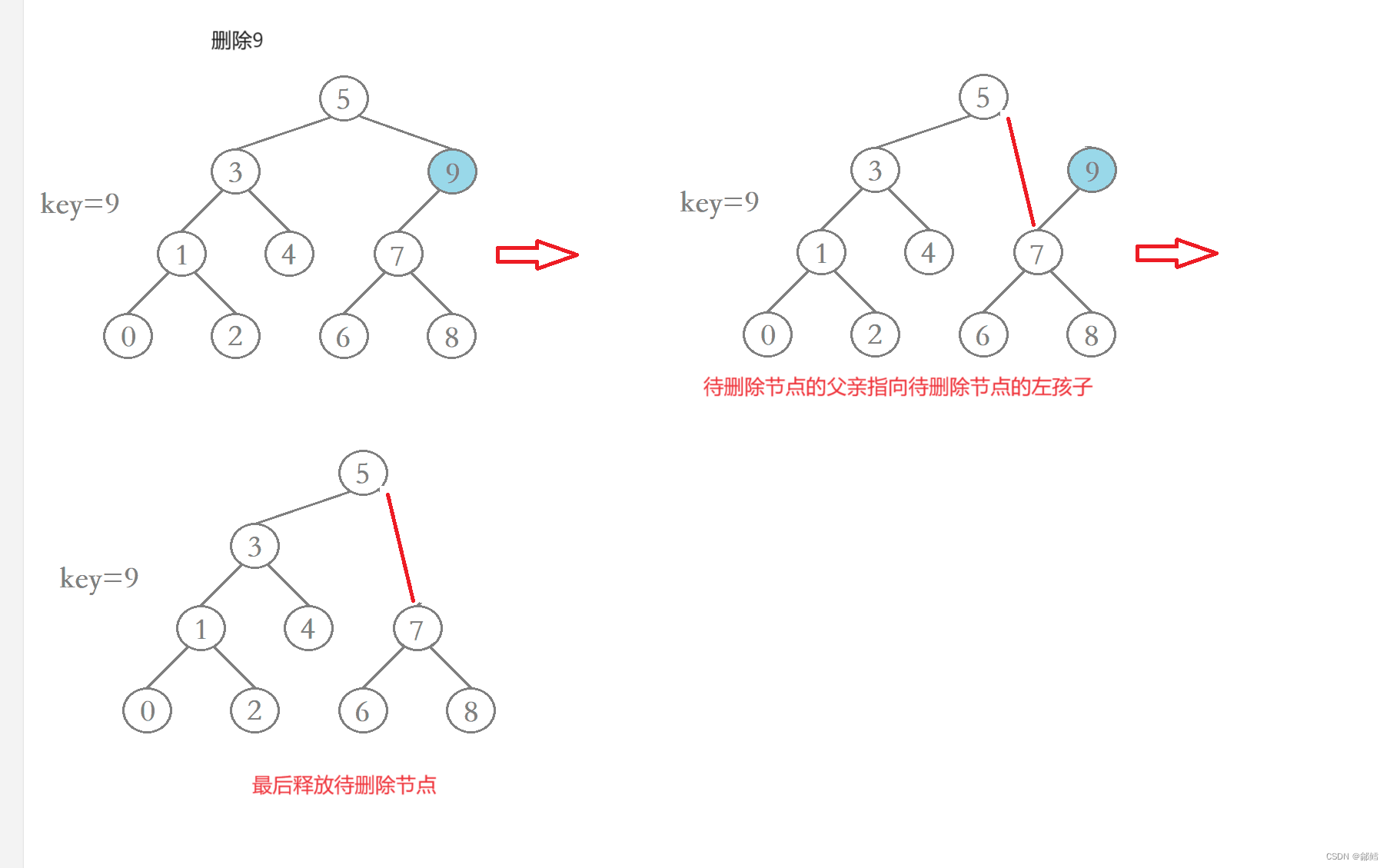
1、2 两种情况,被删除的节点都只有一个孩子
3、待删除结点的左右子树均不为空,即被删除节点有两个孩子
使用替换法处理第3中情况:
1、找替换节点:替换节点一般是左子树的最大节点(最右节点),或者是右子树的最小节点(最左节点)
2、将替换的节点删除
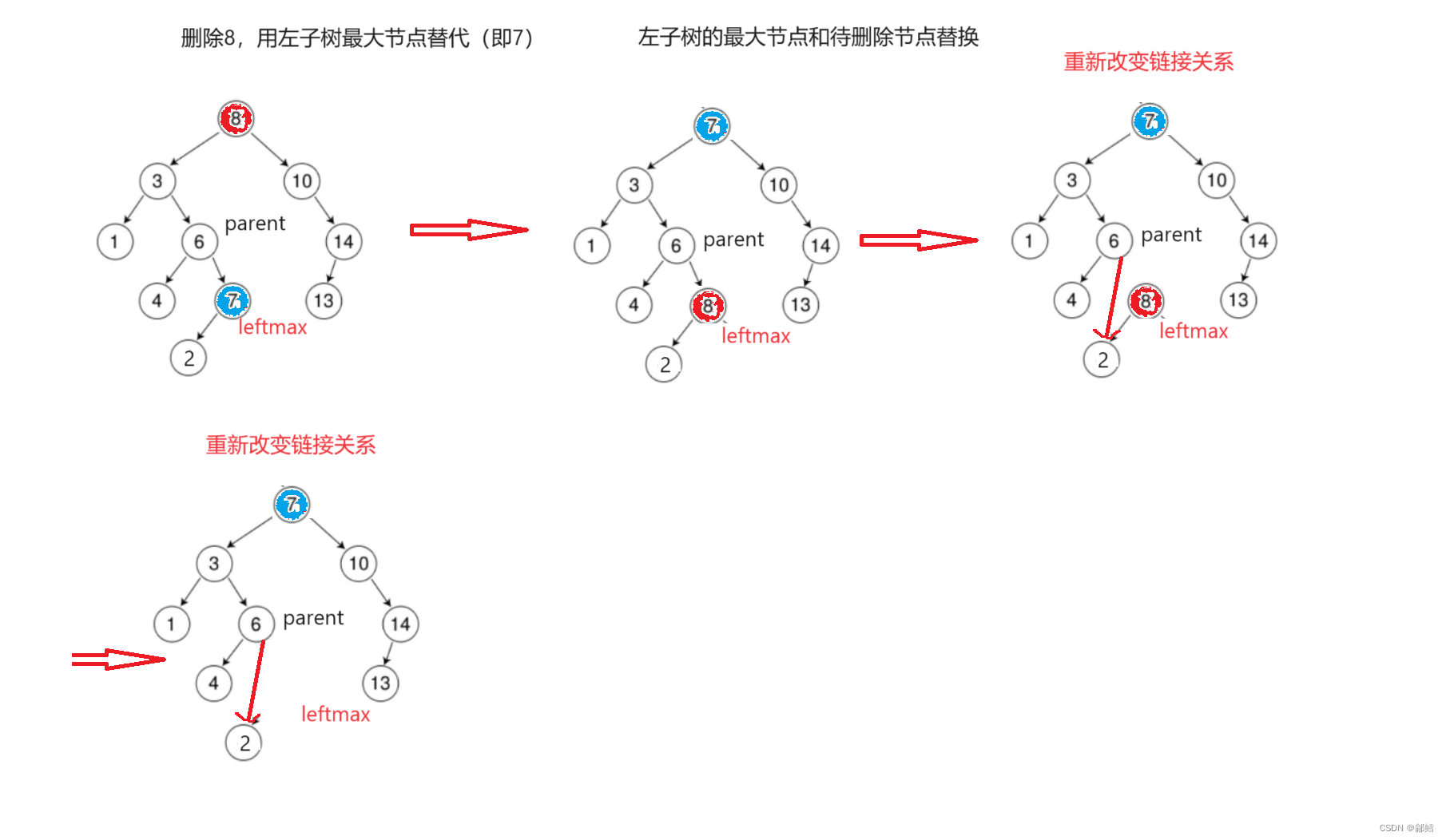
特殊情况:
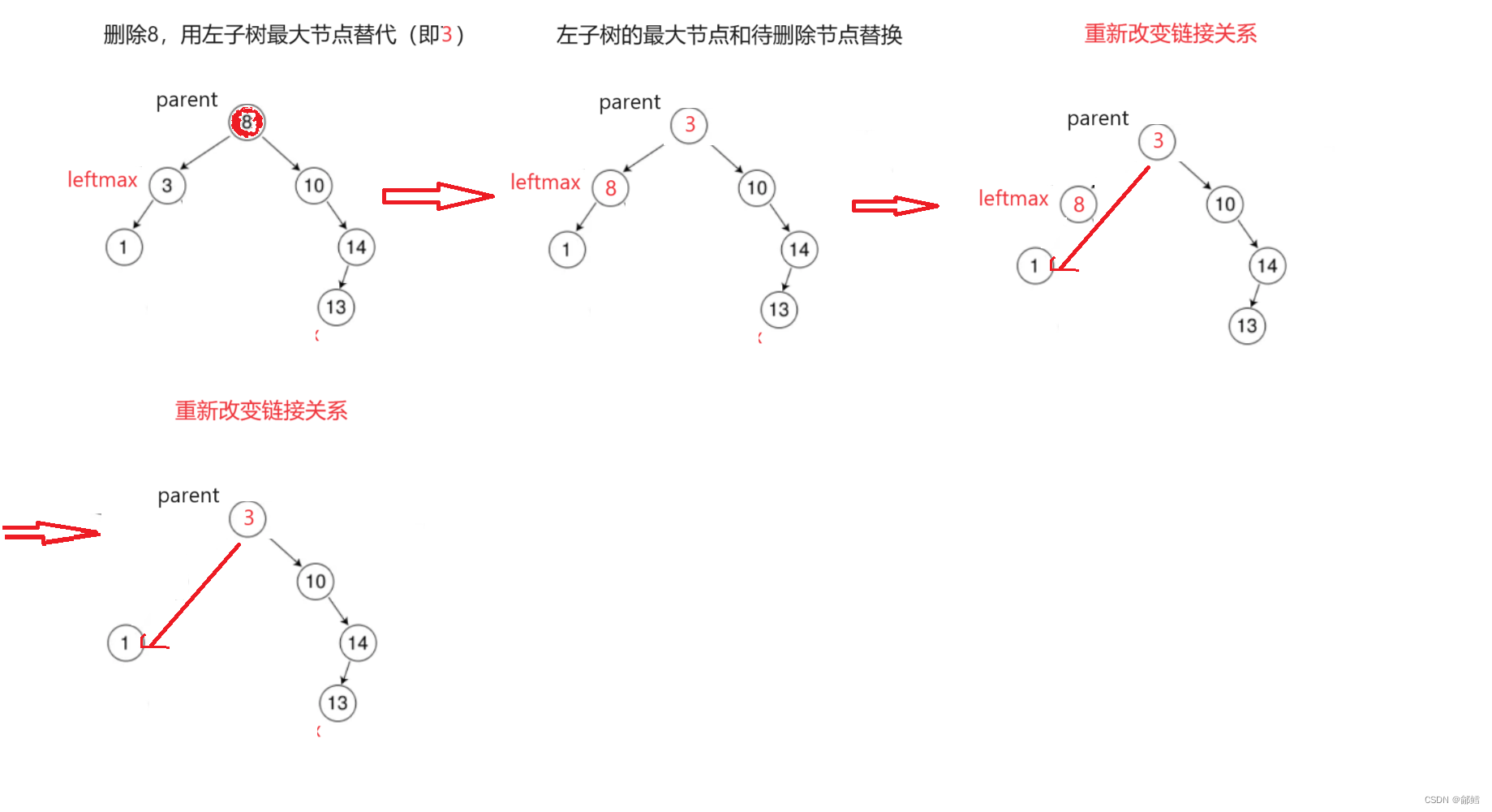
循环
bool Erase(const K& key){Node* parent = nullptr;//待删除节点的父节点Node* cur = _root;//待删除的节点//不是空树while (cur){//往左边走if (cur->_key > key){parent = cur;cur = cur->_left;}//往右边走else if (cur->_key < key){parent = cur;cur = cur->_right;}//找到待删除的节点else{//待删除节点的左子树为空 ,即一个孩子的情况if (cur->_left == nullptr){//待删除节点是根节点if (cur == _root){//将根节点改为待删除节点的右孩子_root = cur->_right;}//待删除节点不是根节点,并且此时parent不为nullptrelse{if (parent->_right == cur){parent->_right = cur->_right;}else//parent->_left ==cur{parent->_left = cur->_right;}}}//待删除节点的右子树为空 ,即一个孩子的情况else if (cur->_right == nullptr){//待删除节点是根节点if (cur == _root){//将根节点改为待删除节点的左孩子_root = cur->_left;}//待删除节点不是根节点,并且此时parent不为nullptrelse{if (parent->_right == cur){parent->_right = cur->_left;}else//parent->_left==cur{parent->_left = cur->_left;}}} else //待删除的节点的左右孩子都不为空 (替换法:左子树的最大节点即最右节点,或者右子树的最小节点即最左节点,并且将替换的节点删除){//替换法//找替代节点Node* parent = cur;//找左子树的最大节点,左子树的最大节点一定没有右孩子Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax; //记录leftMax的父节点,防止删除leftMax时找不到该节点位置 //一直往右子树找leftMax = leftMax->_right;}//左子树的最大节点和待删除节点替换swap(cur->_key, leftMax->_key);//重新改变链接关系//特殊情况 if (parent->_left == leftMax){parent->_left = leftMax->_left;}else//普通情况 parent->_right== leftMax{parent->_right = leftMax->_left;}cur = leftMax;}//删除左子树的最大节点delete cur;return true;}}return false;}
递归
bool EraseR(Node* _root, const K& key)//递归版本{return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key)//引用的目的:不用找父节点,不需要用父节点比较大小{//结束条件if (root == nullptr){return false;}//往左树找if (root->_key > key){return _EraseR(root->_left, key);}//往右树找else if (root->_key < key){return _EraseR(root->_right, key);}else//找到,开始删除{Node* del = root;//待删除节点的左子树为空 ,即一个孩子的情况if (root->_left == nullptr){root = root->_right;}//待删除节点的右子树为空 ,即一个孩子的情况else if (root->_right == nullptr){root = root->_left;}//待删除的节点的左右孩子都不为空 (替换法:左子树的最大节点即最右节点,或者右子树的最小节点即最左节点,并且将替换的节点删除)else{//找左子树最大节点Node* leftMax = root->_left;//一直往左边找,直到找到左子树最大节点while (root->_left){root = root->_left;}//将左子树最大节点与被删除节点替换swap(leftMax->_key, root->_key);return _EraseR(root, key);}delete del;//?return true;}}
Find
循环
bool Find(const K & key){Node* cur = _root;while (cur){if (cur->_left > key){cur = cur->_left;}else if (cur->_left < key){cur = cur->_right;}else{return false;}return true;}}
递归
bool FindR(Node* _root, const K& key)//递归版本{return _FindR(_root, key);}private:bool _FindR(Node* root, const K& key){//结束条件if (root == nullptr){return false;}if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return true;}}
二叉搜索树的应用
K模型
K模型,即只有key作为关键码,结构中只需存储key即可,关键码即为需要搜索到的值。
比如:给定一个单词,判断该单词是否拼写正确。具体方式如下:
void TestBSTree1(){BSTree<string, string > dict;dict.InsertR("insert", "插入");dict.InsertR("sort", "排序");dict.InsertR("right", "右边");dict.InsertR("date", "日期");string str;while (cin>>str){auto * ret = dict.FindR(str);//auto ret = dict.FindR(str);if (ret){cout << ret->_value << endl;}else{cout << "无此单词" << endl;}}}
KV模型
KV模型,对于每一个关键码key,都有与之对应的值value,即<key, value>的键值对。
英汉词典就是英文与中文的对应关系,即<word, Chinese>就构成一种键值对。具体方式如下
1、以<单词, 中文含义>为键值对,构建一棵二叉搜索树。注意:二叉搜索树需要进行比较,键值对比较时只比较key。
2、查询英文单词时,只需给出英文单词就可以快速找到与其对应的中文含义。
完整代码
普通版本
#pragma once template <class K>struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K & key):_left(nullptr),_right(nullptr),_key(key){}
};template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree():_root(nullptr){}bool Insert(const K & key ){//空树if (_root == nullptr){_root = new Node(key);return true;}//不是空树Node* parent = nullptr;//找到父节点Node* cur = _root;while (cur){//比较if (cur->_key < key){//往右子树走parent = cur;cur = cur->_right;}else if (cur->_key > key){//往左子树走parent = cur;cur = cur->_left;}else{return false;}}//插入节点cur = new Node(key);//不知道parent在那一边,需要进一步判断if (parent->_key > key){//parent在左边parent->_left = cur;}else if (parent->_key < key){//parent在右边parent->_right = cur;}else{return false;}return true;}bool Find(const K & key){Node* cur = _root;while (cur){if (cur->_left > key){cur = cur->_left;}else if (cur->_left < key){cur = cur->_right;}else{return false;}return true;}}bool Erase(const K& key){Node* parent = nullptr;//待删除节点的父节点Node* cur = _root;//待删除的节点//不是空树while (cur){//往左边走if (cur->_key > key){parent = cur;cur = cur->_left;}//往右边走else if (cur->_key < key){parent = cur;cur = cur->_right;}//找到待删除的节点else{//待删除节点的左子树为空 ,即一个孩子的情况if (cur->_left == nullptr){//待删除节点是根节点if (cur == _root){//将根节点改为待删除节点的右孩子_root = cur->_right;}//待删除节点不是根节点,并且此时parent不为nullptrelse{if (parent->_right == cur){parent->_right = cur->_right;}else//parent->_left ==cur{parent->_left = cur->_right;}}}//待删除节点的右子树为空 ,即一个孩子的情况else if (cur->_right == nullptr){//待删除节点是根节点if (cur == _root){//将根节点改为待删除节点的左孩子_root = cur->_left;}//待删除节点不是根节点,并且此时parent不为nullptrelse{if (parent->_right == cur){parent->_right = cur->_left;}else//parent->_left==cur{parent->_left = cur->_left;}}} else //待删除的节点的左右孩子都不为空 (替换法:左子树的最大节点即最右节点,或者右子树的最小节点即最左节点,并且将替换的节点删除){//替换法//找替代节点Node* parent = cur;//找左子树的最大节点Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax; //记录leftMax的父节点,防止删除leftMax时找不到该节点位置 //一直往右子树找leftMax = leftMax->_right;}//左子树的最大节点和待删除节点替换swap(cur->_key, leftMax->_key);//重新改变链接关系//特殊情况 if (parent->_left == leftMax){parent->_left = leftMax->_left;}else//普通情况 {parent->_right = leftMax->_left;//parent->_right =nullptr;}cur = leftMax;}//删除左子树的最大节点delete cur;return true;}}return false;}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node *root ){if (root == nullptr){return; }_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root;
};void TestBSTree1()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> t;for (auto e : a){t.Insert(e);}t.InOrder();t.Erase(4);t.InOrder();t.Erase(6);t.InOrder();t.Erase(7);t.InOrder();t.Erase(3);t.InOrder();for (auto e : a){t.Erase(e);}t.InOrder();}
递归版本
#pragma once
#include<string>
using namespace std;
namespace key
{template <class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template <class K>class BSTree{public:typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}~BSTree(){Destroy(_root);}//拷贝构造BSTree(const BSTree<K>& t)//BSTree( BSTree<K> *this , const BSTree<K> & t)//t1 =t {_root = Copy(t._root);}//赋值重载 BSTree<K>& operator= (BSTree<K>& t)//t1 = t{swap(_root, t._root);return *this;}bool EraseR(Node* _root, const K& key)//递归版本{return _EraseR(_root, key);}bool InsertR(const K& key)//递归版本{return _InsertR(_root, key);}bool FindR(Node* _root, const K& key)//递归版本{return _FindR(_root, key);}private:Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* copyNode = new Node(root->_key);//递归 copyNode->_left = Copy(root->_left);copyNode->_right = Copy(root->_right);return copyNode;}void Destroy(Node*& root) //引用的目的:将每个节点释放后同时置空{//后序遍历 if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _InsertR(Node*& root, const K& key) //引用的目的:不用找父节点,不需要用父节点比较大小{//结束条件if (root == nullptr){root = new Node(key);return true;}//往左子树走if (root->_key > key){return _InsertR(root->_left, key);}//往右子树走else if (root->_key < key){return _InsertR(root->_right, key);}else{return false;}}bool _EraseR(Node*& root, const K& key)//引用的目的:不用找父节点,不需要用父节点比较大小{//结束条件if (root == nullptr){return false;}//往左树找if (root->_key > key){return _EraseR(root->_left, key);}//往右树找else if (root->_key < key){return _EraseR(root->_right, key);}else//找到,开始删除{Node* del = root;//待删除节点的左子树为空 ,即一个孩子的情况if (root->_left == nullptr){root = root->_right;}//待删除节点的右子树为空 ,即一个孩子的情况else if (root->_right == nullptr){root = root->_left;}//待删除的节点的左右孩子都不为空 (替换法:左子树的最大节点即最右节点,或者右子树的最小节点即最左节点,并且将替换的节点删除)else{//找左子树最大节点Node* leftMax = root->_left;//一直往左边找,直到找到左子树最大节点while (root->_left){root = root->_left;}//将左子树最大节点与被删除节点替换swap(leftMax->_key, root->_key);return _EraseR(root, key);}delete del;//?return true;}}bool _FindR(Node* root, const K& key){//结束条件if (root == nullptr){return false;}if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return true;}}public://中序遍历void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}public:Node* _root;};void TestBSTree1(){int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> t;for (auto e : a){t.InsertR(e);}t.InOrder();//没有引用,释放了,只是指针没有置空,尤其是根节点_root,我们还能通过他找到/*t.Destroy(t._root);*/t.EraseR(t._root, 4);t.InOrder();t.EraseR(t._root, 6);t.InOrder();t.EraseR(t._root, 7);t.InOrder();t.EraseR(t._root, 3);t.InOrder();for (auto e : a){t.EraseR(t._root, e);}t.InOrder();}void TestBSTree2(){int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> t;for (auto e : a){t.InsertR(e);}t.InOrder();BSTree<int> t1(t);t.InOrder();t1.InOrder();}
}namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{public:typedef BSTreeNode<K, V> Node;public:BSTree():_root(nullptr){}void InOrder(){_InOrder(_root);cout << endl;}Node* FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key, const V& value){return _InsertR(_root, key, value);}bool EraseR(const K& key){return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;// 1、左为空// 2、右为空// 3、左右都不为空if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key, const V& value){if (root == nullptr){root = new Node(key, value);return true;}if (root->_key < key){return _InsertR(root->_right, key, value);}else if (root->_key > key){return _InsertR(root->_left, key, value);}else{return false;}}Node* _FindR(Node* root, const K& key){if (root == nullptr)return nullptr;if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return root;}}void _InOrder(Node* root){if (root == NULL){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root;};void TestBSTree1(){BSTree<string, string > dict;dict.InsertR("insert", "插入");dict.InsertR("sort", "排序");dict.InsertR("right", "右边");dict.InsertR("date", "日期");string str;while (cin>>str){auto * ret = dict.FindR(str);//auto ret = dict.FindR(str);if (ret){cout << ret->_value << endl;}else{cout << "无此单词" << endl;}}}void TestBSTree2(){string arr[] = {"西瓜", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int > countTree;for (auto &str : arr){auto ret = countTree.FindR(str);if (ret == nullptr){countTree.InsertR(str,1);}else{ret->_value++;}}countTree.InOrder();}}如果你觉得这篇文章对你有帮助,不妨动动手指给点赞收藏加转发,给鄃鳕一个大大的关注你们的每一次支持都将转化为我前进的动力!!!
相关文章:

搜索二叉树【C++】
文章目录 二叉搜索树二叉搜索树的模拟实现构造函数拷贝构造函数赋值运算符重载函数析构函数Insert循环递归 Erase循环递归 Find循环递归 二叉搜索树的应用K模型KV模型 完整代码普通版本递归版本 二叉搜索树 二叉搜索树又称为二叉排序树,它或者是一棵空树࿰…...
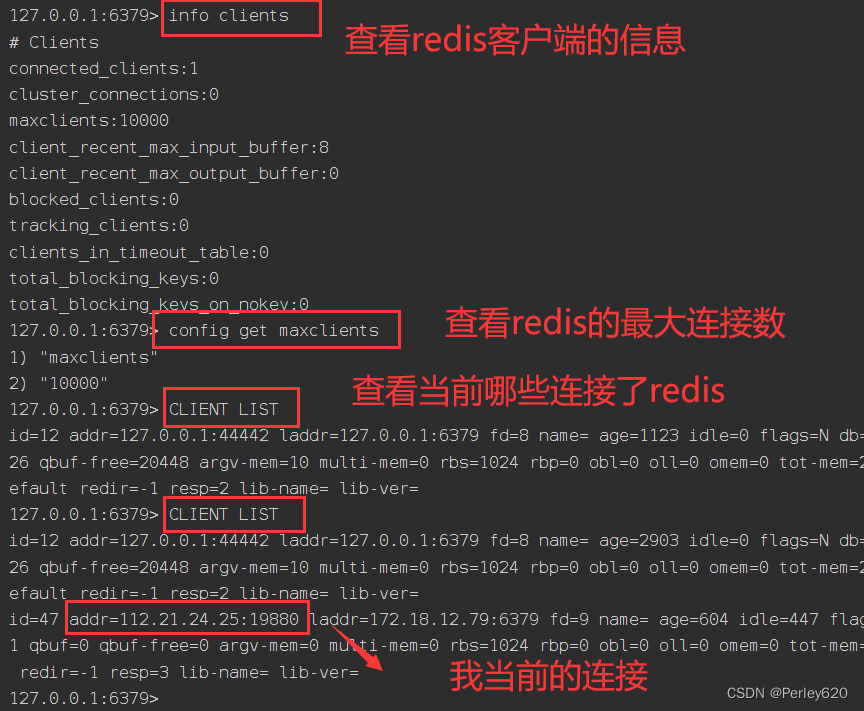
华为云云耀云服务器L实例评测|认识redis未授权访问漏洞 漏洞的部分复现 设置连接密码 redis其他命令学习
前言 最近华为云云耀云服务器L实例上新,也搞了一台来玩,期间遇到过MySQL数据库被攻击的情况,数据丢失,还好我有几份备份,没有造成太大的损失。昨天收到华为云的邮箱提醒,我的redis数据库没有设置密码&…...

快速安装NGINX
快速安装NGINX #安装依赖包 yum -y install gcc pcre pcre-devel zlib zlib-devel openssl openssl-devel#下载NGINX curl -O https://nginx.org/download/nginx-1.21.6.tar.gz#解压NGINX tar -zxvf nginx-1.21.6.tar.gz cd nginx-1.21.6.tar.gz#配置 ./configure --prefix/…...
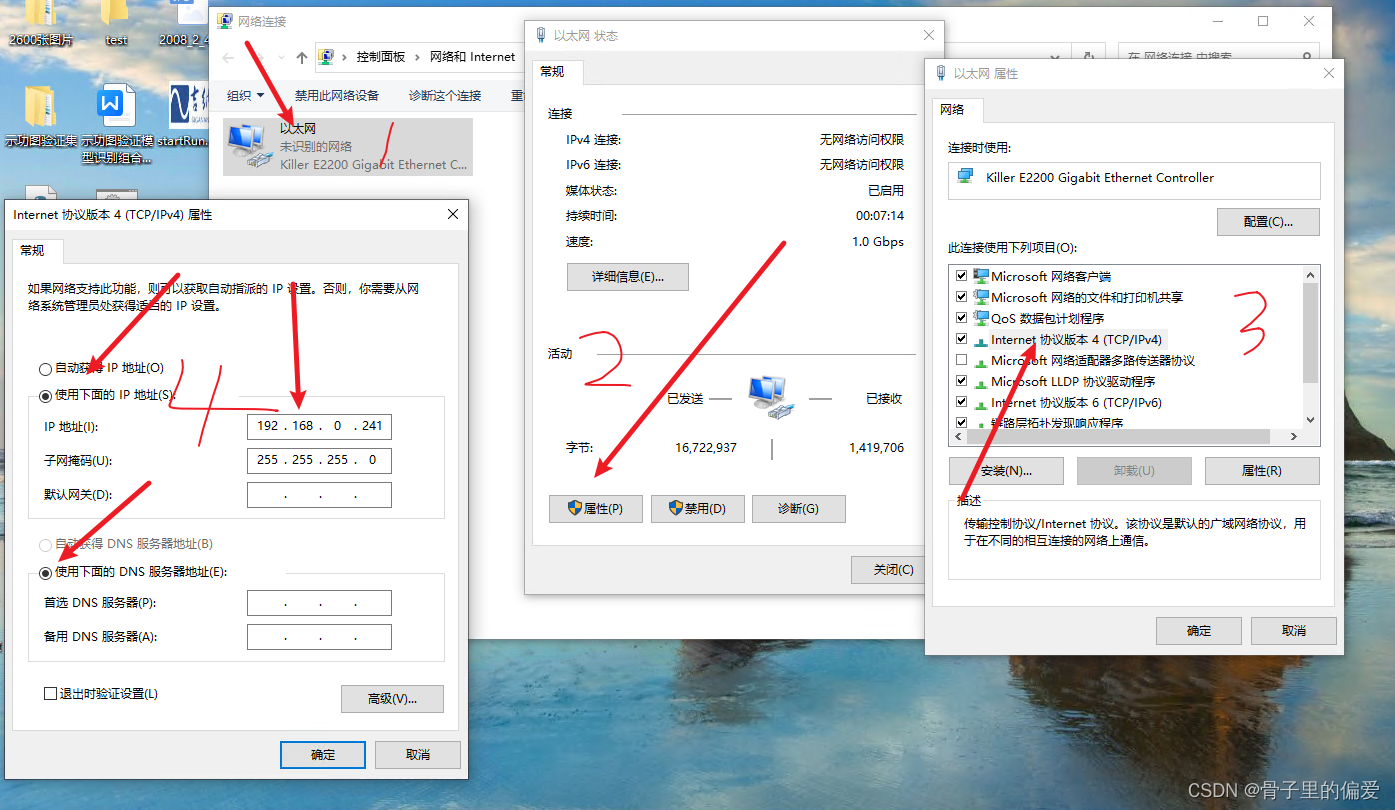
一台电脑远程内网的另外一台电脑,禁止远程的电脑连接外网,只允许内网连接
一台电脑远程内网的另外一台电脑,禁止远程的电脑连接外网,只允许内网连接 1.找到右下角网卡图标,右键图标选择“打开网络和共享中心”。 3、点击“更改适配器设置”。 4、右键正在使用的网卡“本地连接”打开属性 5、找到“internet协…...

山西电力市场日前价格预测【2023-09-24】
日前价格预测 预测说明: 如上图所示,预测明日(2023-09-24)山西电力市场全天平均日前电价为496.09元/MWh。其中,最高日前电价为705.54元/MWh,预计出现在14: 30。最低日前电价为333.70元/MWh,预计…...

MQ---第二篇
系列文章目录 文章目录 系列文章目录一、RabbitMQ事务消息二、RabbitMQ死信队列、延时队列一、RabbitMQ事务消息 通过对信道的设置实现 channel.txSelect();通知服务器开启事务模式;服务端会返回Tx.Select-Okchannel.basicPublish;发送消息,可以是多条,可以是消费消息提交…...

C++ 创建文件并写入内容
文章目录 1.问题2.filesystem3.示例参考文献 1.问题 C 如何向指定路径的文件写入内容呢? 这里有几点要求: 如果目录不存在需要自动创建。如果文件不存在需要自动创建。以覆盖的方式写入内容。 2.filesystem C17 带来了一个新的库:filesy…...

微信小程序rich-text里面写多行溢出显示省略号在ios中不显示的问题
问题:微信小程序rich-text里面写多行溢出显示省略号在ios中不显示的问题 解决方法:需要给一个默认的div标签,在div写行内样式 overflow : hidden; text-overflow: ellipsis; display: -webkit-box; -webkit-line-clamp: 3; -webkit-box-o…...
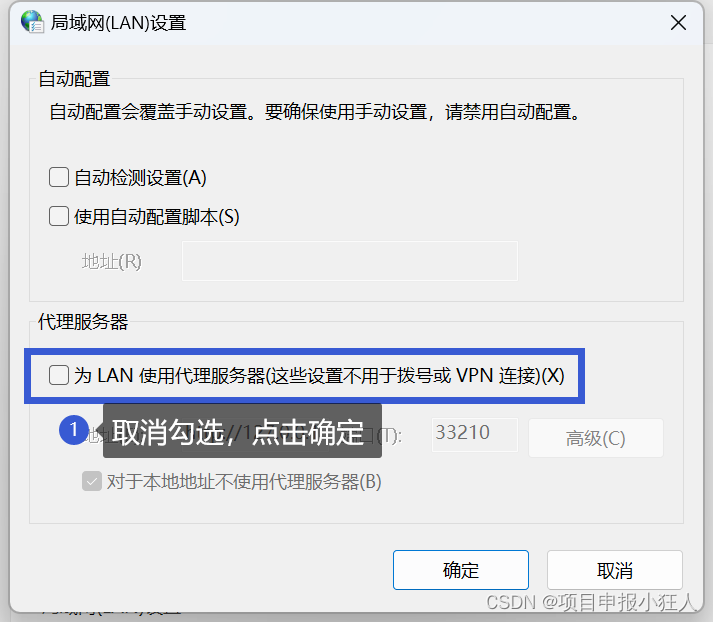
解决Win11/10中Edge浏览器页面加载不出来、打不开问题|有网但是打不开,加载不了
问题症状 edge浏览器打不开,有网络能正常上网,但是edge浏览器无法浏览。网络质量很高,但是页面就是加载不出来,详情如下: (我是在科学上网后造成这样子的原因,现在将我的方法分享一下ÿ…...

【DRAM存储器五】DRAM存储器的架构演进-part2
👉个人主页:highman110 👉作者简介:一名硬件工程师,持续学习,不断记录,保持思考,输出干货内容 参考书籍:《Memory Systems - Cache, DRAM, Disk》 目录 以提升吞吐…...
分享一个基于uniapp+springboot技术开发的校园失物招领小程序(源码、lw、调试)
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
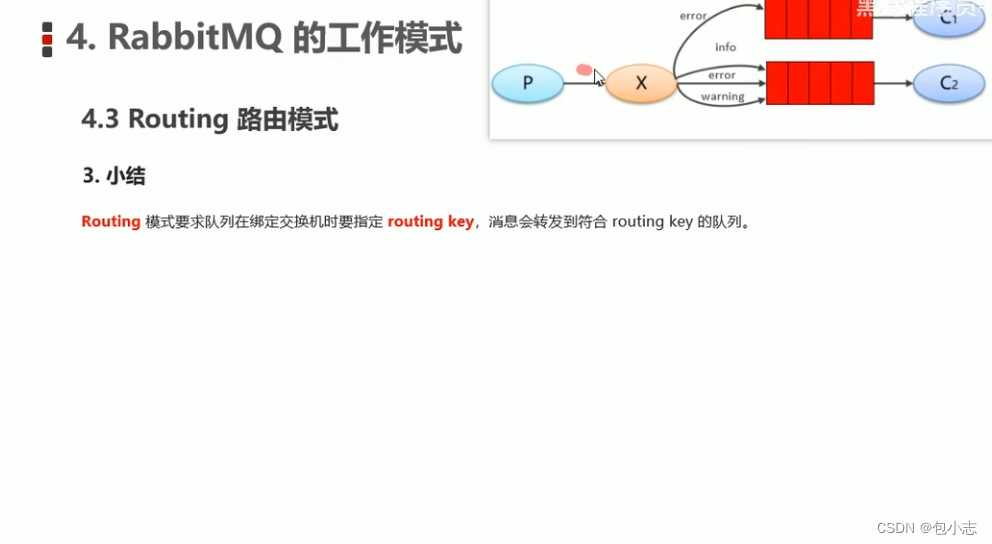
RabbitMQ工作模式——Routing路由模式
1.Routing路由模式 Routing生产者代码 public class Producer_Routing {public static void main(String[] args) throws IOException, TimeoutException {//1.创建连接工厂ConnectionFactory factory new ConnectionFactory();//2.设置参数factory.setHost("172.16.98.…...

Python字典的增删改查以及嵌套
嗨喽,大家好呀~这里是爱看美女的茜茜呐 👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~ python源码、视频教程、插件安装教程、资料我都准备好了,直接在文末名片自取就可 字典 基础数…...

【淘宝开店】新手入门开网店教程
一、上架产品流程顺序 1. 上架10个产品2. 早中晚各上架1件产品3. 连续上架4天 二、产品培训 动销率要求: 店铺产品数必须>10公式: 店铺最近30天有销量产品数 / 店铺上架总产品数 * 100%1. 从动销率可以得出, 店铺产品不宜过多2. 小卖家前期最佳建议产品数10个 三、上架产品…...
(五)(TCP拥塞控制))
计网第五章(运输层)(五)(TCP拥塞控制)
目录 一、基本概念 二、拥塞控制算法 慢开始: 拥塞避免: 快重传: 快恢复: 一、基本概念 若对网络中某一资源的需求超过了该资源所能提供的可用部分(供不应求),网络性能就会变坏。 在计算…...
windows/ubuntu怎么修改hosts文件
windows系统修改方法: 第一步:用管理员权限打开记事本,或者visual studio。 第二步:用记事本或者vs打开地址C:\Windows\System32\drivers\etc\hosts文件,这个时候就可以直接修改了 Ubuntu22 LTS系统修改方法…...
大数据基础知识点1-关系型数据库)
(日积月累版)大数据基础知识点1-关系型数据库
好久不见,甚是想念。 笔者最近有时间整理关于大数据的一些基础知识点,整理的目不在于能提升多少技能,关键在于巩固一些很基础的知识点,毕竟互联网就是基础略稳固的人比较有优势,在遇到或发现一些技术问题时,…...

【开心消消乐】python实现-附ChatGPT解析
1.题目 开心消消乐 知识点编程基础:深搜、广搜 时间限制: 1s 空间限制: 256MB 限定语言:不限 题目描述: 给定一个N行M列的二维矩阵,矩阵中每个位置的数宁取值为0或1。矩阵示例如: 1 1 0 0 0 0 0 1 0 0 1 1 1 1 1 1 现需要将矩阵中所有的1进行反转为0,规则如下: 1)、当点击一…...

springBoot源码汇总
SpringFactoriesLoader 示例位置 SpringApplication#getSpringFactoriesInstances 加载spring.factroies下的初始化类 ClassLoader classLoader this.getClassLoader();Set<String> names new LinkedHashSet(SpringFactoriesLoader.loadFactoryNames(type, classLoade…...

代码随想录二刷day39
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣62. 不同路径二、力扣63. 不同路径 II 前言 一、力扣62. 不同路径 class Solution {public int uniquePaths(int m, int n) {int[][] dp new int[m][…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
