数据结构-----堆(完全二叉树)
目录
前言
一.堆
1.堆的概念
2.堆的存储方式
二.堆的操作方法
1.堆的结构体表示
2.数字交换接口函数
3.向上调整(难点)
4.向下调整(难点)
5.创建堆
6.堆的插入
7.判断空
8.堆的删除
9.获取堆的根(顶)元素
10.堆的遍历
11.销毁堆
完整代码
三.堆的应用(堆排序)
1.算法介绍
2.基本思想
3.代码实现
4.算法分析
前言
今天我们开始学习一种二叉树,没错,那就是完全二叉树,完全二叉树又叫做堆,在此之前我们简单介绍过了完全二叉树的概念(链接:数据结构-----树和二叉树的定义与性质_灰勒塔德的博客-CSDN博客),这种类型的二叉树又有什么特点呢?代码怎么去实现呢?应用有那些呢?下面就一起来看看吧!
一.堆
1.堆的概念
堆(heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象,物理层面上是一个数组,逻辑上是一个完全二叉树。堆总是满足下列性质:
堆中某个结点的值总是不大于或不小于其父结点的值;
堆总是一棵完全二叉树。

满足任意父节点都大于子节点的称作为大堆
满足任意子节点都大于父节点的称作为小堆
tip:(下文会以大堆的创建为示例)
如图所示:
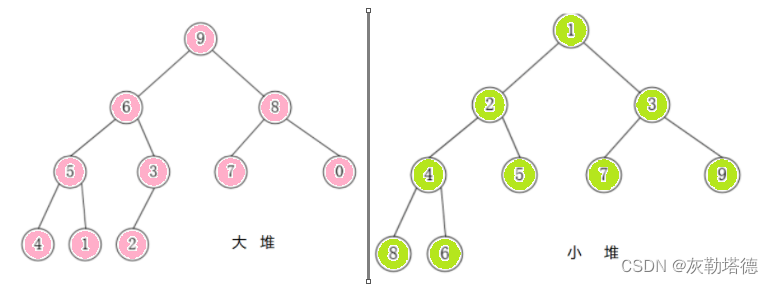
2.堆的存储方式
堆的储存原则是从上到下,从左到右,也就是说先有上面的父节点才会有子节点,先有左子节点,才会有右子节点 ,所以堆可以去通过一个数组完整的表示出来,如下图所示:

二.堆的操作方法
以下是一个堆要实现的基本功能,下面我会一一去详细解释说明
void swap(DataType* a, DataType* b);//交换数据void Adjust_Up(DataType* data, int child, int n);//向上调整void Adjust_Down(DataType* data, int parent, int n);//向下调整void Heap_Create(Heap* hp, DataType* data, int n);//创建堆bool isEmpty(Heap* hp);//判断空void Heap_Insert(Heap* hp, DataType x);//堆的插入void Heap_Del(Heap* hp);//堆的删除操作DataType Heap_Root(Heap* hp);//获取根元素void Heap_show(Heap* hp);//堆的遍历void Heap_Destory(Heap* hp);//堆的销毁1.堆的结构体表示
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define Maxsize 50//顺序结构
//堆(完全二叉树)
typedef int DataType; //定义数据的类型
typedef struct Heap
{int size; //当前节点数量int capacity; //最大容量DataType* data; //数据储存地址
}Heap;
2.数字交换接口函数
//数据交换接口
void swap(DataType* a, DataType* b) {DataType temp = *a;*a = *b;*b = temp;
}3.向上调整(难点)
创建大堆时,向上调整的目的是,在有子节点位置的情况下,进行与父节点的大小比较,如果子节点大于父节点,那么就进行交换,然后新的子节点就是上一个的父节点,依次这样比较下去,最后到根节点为止,如图所示:
 代码实现:
代码实现:
//向上调整
void Adjust_Up(DataType* data, int child, int n) {int parent = (child - 1) / 2;while (child > 0) {//如果子节点大于父节点就进行数值交换,然后此时的子节点就是前一个父节点,再找到//新的父节点,继续进行同样的操作,直到根节点为止if (data[child] > data[parent]){swap(&data[child], &data[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}4.向下调整(难点)
同样的还有向下调整,如果有了当前的父节点位置,那么就要跟子节点进行比较,但是子节点有左和右子节点,所以左右子节点也要去比较,取到其中比较大的子节点与父节点比较,如果这个字节点大于父节点的话,那就进行数字交换,然后新的父节点就是上一个的子节点,依次往下遍历进行同样的操作。

代码实现:
//向下调整
void Adjust_Down(DataType* data, int parent, int n) {int child = parent * 2 + 1;while (child <n ) {if (child+1 < n && data[child] < data[child+1]){//如果右子节点大于左子节点,那就child+1,选中到右子节点child++;}if (data[child] > data[parent]) {//同样的,有了当前父节点,然后找到子节点,进行向下遍历调整操作swap(&data[child], &data[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}5.创建堆
已有一个数组{ 5,1,2,3,6,4,8 },怎么把这个数组放入堆里面呢?同样的,空间申请去申请到一块连续的空间,然后依次把数据存入到这个数组里面去,最后进行向下调整,以达到堆的形式。
放入堆之后如下图所示:

代码实现:
//创建堆
void Heap_Create(Heap* hp, DataType* data, int n) {assert(hp);hp->data = (DataType*)malloc(sizeof(DataType) * n);if (!hp->data) {printf("ERROR\n");exit(-1);}for (int i = 0; i < n; i++) {hp->data[i] = data[i];//赋值}hp->size = n;hp->capacity = Maxsize;for (int j = (n - 1) / 2; j >= 0; j--) {//创建完成了之后,就要进行向下调整Adjust_Down(hp->data, j ,hp->size);}
}6.堆的插入
堆的插入,就是在堆的最后面去添加一个元素,添加完成之后,就要去进行向上调整操作,如下图所示:

代码实现:
//堆的插入
void Heap_Insert(Heap* hp, DataType x) {assert(hp);//如果此时的堆空间满了,那么就要去扩容空间if (hp->size == hp->capacity) {DataType* temp = (DataType*)realloc(hp->data,sizeof(DataType) * (hp->capacity+1));//追加1个空间if (!temp) {printf("ERROR\n");exit(-1);}hp->data = temp;hp->data[hp->size] = x;hp->size++;hp->capacity++;}else{hp->data[hp->size] = x;hp->size++;}Adjust_Up(hp->data, hp->size - 1, hp->size);//插入后进行向上调整
}7.判断空
//判断空
bool isEmpty(Heap* hp) {assert(hp);return hp->size == 0;
}8.堆的删除
堆的删除操作是删除掉根节点,过程是,先把最后一个节点与根节点进行交换,然后重新进行向下调整。(堆的删除操作,删除掉的是根节点!)

代码实现:
//堆的删除,删除根节点
void Heap_Del(Heap* hp) {assert(hp);if (!isEmpty(hp)) {swap(&hp->data[hp->size - 1], &hp->data[0]);//根节点和尾节点进行交换hp->size--;Adjust_Down(hp->data, 0, hp->size);//向下调整}
}9.获取堆的根(顶)元素
//获取堆顶元素
DataType Heap_Root(Heap* hp) {assert(hp);if (!isEmpty(hp))return hp->data[0];elseexit(0);
}10.堆的遍历
堆的遍历就直接按照数组的顺序去遍历就行了,完全二叉树的逻辑上是从上到下,从左到右去遍历的,代码如下:
//输出堆元素(按照顺序)
void Heap_show(Heap* hp) {assert(hp);if (isEmpty(hp)) {printf("The Heap is etmpy\n");return;}for (int i = 0; i < hp->size; i++)printf("%d ", hp->data[i]);
}11.销毁堆
//堆的销毁
void Heap_Destory(Heap* hp) {assert(hp);hp->size = hp->capacity = 0;free(hp);//释放空间
}完整代码
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define Maxsize 50//顺序结构
//堆(完全二叉树)
typedef int DataType; //定义数据的类型
typedef struct Heap
{int size; //当前节点数量int capacity; //最大容量DataType* data; //数据储存地址
}Heap;//数据交换接口
void swap(DataType* a, DataType* b) {DataType temp = *a;*a = *b;*b = temp;
}//向上调整
void Adjust_Up(DataType* data, int child, int n) {int parent = (child - 1) / 2;while (child > 0) {//如果子节点大于父节点就进行数值交换,然后此时的子节点就是前一个父节点,再找到//新的父节点,继续进行同样的操作,直到根节点为止if (data[child] > data[parent]){swap(&data[child], &data[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下调整
void Adjust_Down(DataType* data, int parent, int n) {int child = parent * 2 + 1;while (child <n ) {if (child+1 < n && data[child] < data[child+1]){//如果右子节点大于左子节点,那就child+1,选中到右子节点child++;}if (data[child] > data[parent]) {//同样的,有了当前父节点,然后找到子节点,进行向下遍历调整操作swap(&data[child], &data[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//创建堆
void Heap_Create(Heap* hp, DataType* data, int n) {assert(hp);hp->data = (DataType*)malloc(sizeof(DataType) * n);if (!hp->data) {printf("ERROR\n");exit(-1);}for (int i = 0; i < n; i++) {hp->data[i] = data[i];//赋值}hp->size = n;hp->capacity = Maxsize;for (int j = (n - 1) / 2; j >= 0; j--) {//创建完成了之后,就要进行向下调整Adjust_Down(hp->data, j ,hp->size);}
}//判断空
bool isEmpty(Heap* hp) {assert(hp);return hp->size == 0;
}//堆的插入
void Heap_Insert(Heap* hp, DataType x) {assert(hp);//如果此时的堆空间满了,那么就要去扩容空间if (hp->size == hp->capacity) {DataType* temp = (DataType*)realloc(hp->data,sizeof(DataType) * (hp->capacity+1));//追加1个空间if (!temp) {printf("ERROR\n");exit(-1);}hp->data = temp;hp->data[hp->size] = x;hp->size++;hp->capacity++;}else{hp->data[hp->size] = x;hp->size++;}Adjust_Up(hp->data, hp->size - 1, hp->size);//插入后进行向上调整
}//堆的删除,取出根节点
void Heap_Del(Heap* hp) {assert(hp);if (!isEmpty(hp)) {swap(&hp->data[hp->size - 1], &hp->data[0]);//根节点和尾节点进行交换hp->size--;Adjust_Down(hp->data, 0, hp->size);//向下调整}
}//获取堆顶元素
DataType Heap_Root(Heap* hp) {assert(hp);if (!isEmpty(hp))return hp->data[0];elseexit(0);
}//输出堆元素(按照顺序)
void Heap_show(Heap* hp) {assert(hp);if (isEmpty(hp)) {printf("The Heap is etmpy\n");return;}for (int i = 0; i < hp->size; i++)printf("%d ", hp->data[i]);
}//堆的销毁
void Heap_Destory(Heap* hp) {assert(hp);hp->size = hp->capacity = 0;free(hp);//释放空间
}三.堆的应用(堆排序)
1.算法介绍
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
2.基本思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
① 将待排序的序列构造成一个最大堆,此时序列的最大值为根节点
② 依次将根节点与待排序序列的最后一个元素交换
③ 再维护从根节点到该元素的前一个节点为最大堆,如此往复,最终得到一个递增序列
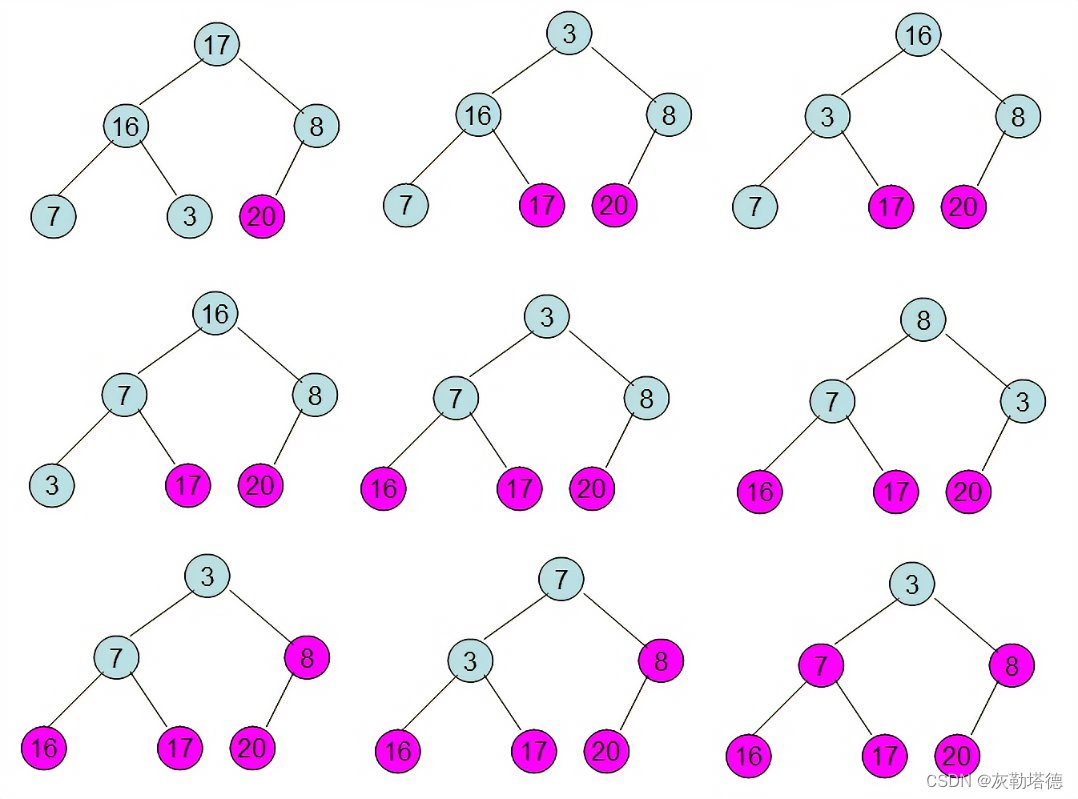
3.代码实现
#include<stdio.h>
#include<assert.h>
//数据交换接口
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}//向下调整
void Adjust_Down(int* data, int parent, int n) {int child = parent * 2 + 1;while (child < n) {if (child + 1 < n && data[child] < data[child + 1]){//如果右子节点大于左子节点,那就child+1,选中到右子节点child++;}if (data[child] > data[parent]) {//同样的,有了当前父节点,然后找到子节点,进行向下遍历调整操作swap(&data[child], &data[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//堆排序算法
void Heap_sort(int* arr, int n) {assert(arr);for (int i = (n - 2) / 2; i >= 0; i--) {Adjust_Down(arr, i, n);}//先形成最大堆int end = n - 1;//从小到大排序while (end > 0) {swap(&arr[0], &arr[end]);Adjust_Down(arr, 0, end);end--; //此时最后一个也就是当前的最大值已经排序好了}
}int main() {int a[9] = { 5,1,2,3,6,4,8,2,10 };Heap_sort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++) {printf("%d ", a[i]);}
}
//输出
//1 2 2 3 4 5 6 8 104.算法分析
- 平均时间复杂度:O(nlogn)
- 最佳时间复杂度:O(nlogn)
- 最差时间复杂度:O(nlogn)
- 稳定性:不稳定
以上就是本期的内容,我们下次见!
分享一张壁纸:
相关文章:

数据结构-----堆(完全二叉树)
目录 前言 一.堆 1.堆的概念 2.堆的存储方式 二.堆的操作方法 1.堆的结构体表示 2.数字交换接口函数 3.向上调整(难点) 4.向下调整(难点) 5.创建堆 6.堆的插入 7.判断空 8.堆的删除 9.获取堆的根(顶)元素 10.堆的遍历…...

set/multiset容器、map容器
目录 set/multiset容器 set基本概念 set大小和交换 set插入和删除 查找和统计 set和multiset的区别 改变set排序规则 set存放内置数据类型 set存放自定义数据类型 pair队组 map容器 map容器的基本概念 map构造和赋值 map大小和交换 map插入和删除 map查找和统计…...
)
Linux系统编程——总结初识Linux(常用命令、特点、常见操作系统)
文章目录 UNIX操作系统(了解)Linux操作系统主要特征Linux和unix的区别和联系什么是操作系统常见的操作系统Ubuntu操作系统Ubuntu安装linux下的目录的类型(掌握)shell指令shell指令的格式文件操作相关指令系统相关命令网络相关命令其他命令软件安装相关的…...

Js使用ffmpeg进行视频剪辑和画面截取
ffmpeg 使用场景是需要在web端进行视频的裁剪,包括使用 在线视频url 或 本地视频文件 的裁剪,以及对视频内容的截取等功能。 前端进行视频操作可能会导致性能下降,最好通过后端使用java,c进行处理,本文的案例是备选方…...

Linux基本命令,基础知识
进到当前用户目录:cd ~ 回到上级目录:cd .. 查看当前目录层级:pwd 创建目录:mkdir mkdir ruanjian4/linux/zqm41 -p级联创建文件夹(同时创建多个文件夹需要加-p) 查看详细信息:ls -l (即 ll) 查看所有详细信息:ls -al 隐藏文件是以.开头的 查看:l…...
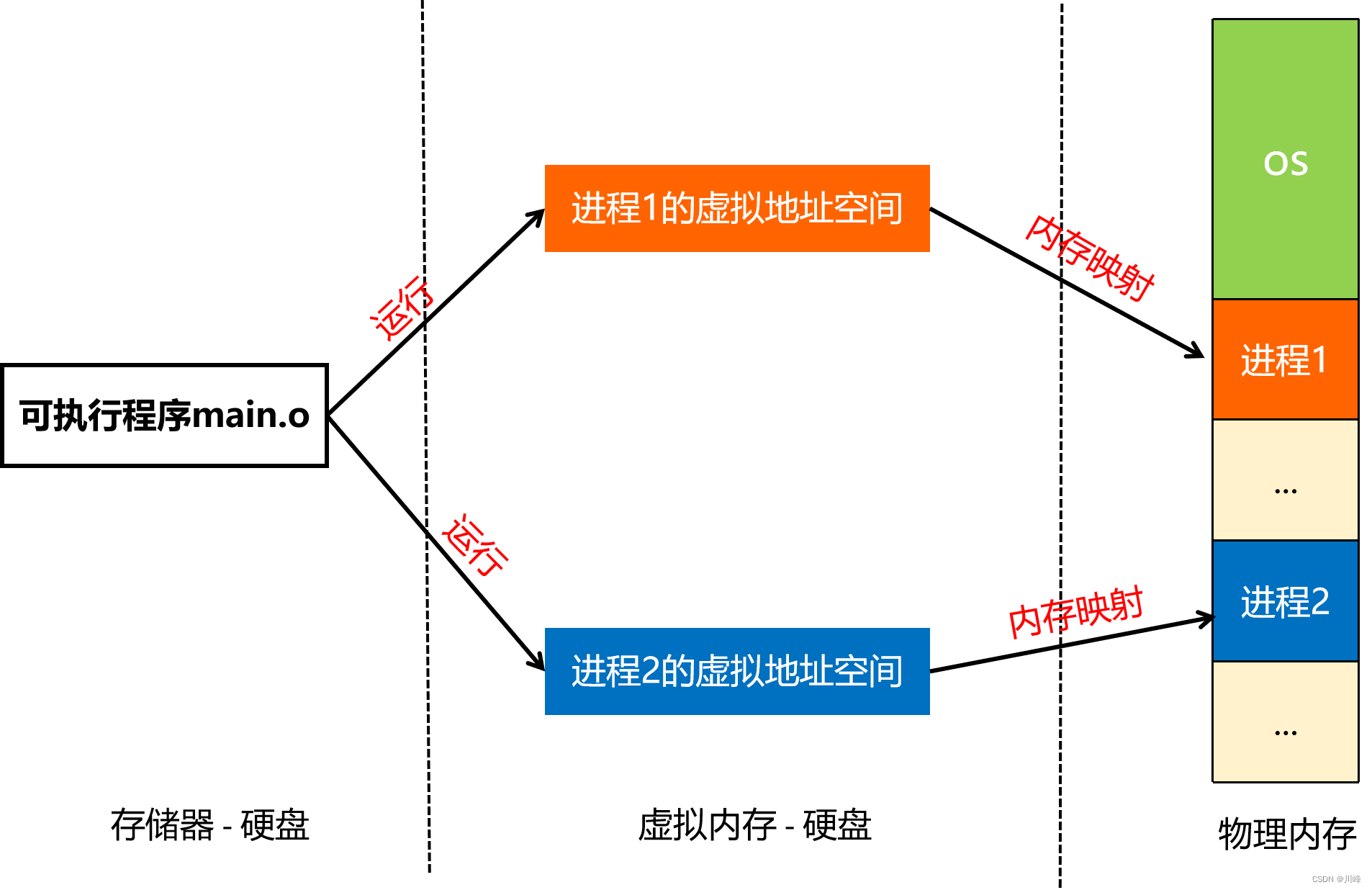
【Android知识笔记】进程通信(三)
在上一篇探索Binder通信原理时,提到了内存映射的概念,其核心是通过mmap函数,将一块 Linux 内核缓存区映射到一块物理内存(匿名文件),这块物理内存其实是作为Binder开辟的数据接收缓存区。这里有两个概念,需要理解清楚,那就是操作系统中的虚拟内存和物理内存,理解了这两…...

云上亚运:所使用的高新技术,你知道吗?
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 公众号:网络豆云计算学堂 座右铭:低头赶路,敬事如仪 个人主页: 网络豆的主页 目录 前言 一.什么是云上亚运会 二.为什么要使用云…...

数据结构简述,时间、空间复杂度,学习网站推荐
目录 IT 学习路线 相关坚韧大厚书 相关有趣/耐看书或视频 数据结构与算法学习网站推荐 刷题 时间、空间复杂度 数据结构简述 基本概念 数据结构与算法简述和CS综述整理。本文非基础的教程,本文会列出大量学习和参考网站。老惯例,一个文章是一个集…...
在线安装qt5.15之后任意版本
下载qt现在安装包: window安装包链接 进入cmd,用命令行打开安装包,并指定组件下载地址(这个是关键,之前用的是腾讯镜像,出现了版本灰色无法选中问题) .\qt-unified-windows-x64-4.6.1-online…...
【kafka实战】01 3分钟在Linux上安装kafka
本节采用docker安装Kafka。采用的是bitnami的镜像。Bitnami是一个提供各种流行应用的Docker镜像和软件包的公司。采用docker的方式3分钟就可以把我们想安装的程序运行起来,不得不说真的很方便啊,好了,开搞。使用前提:Linux虚拟机&…...

yum安装mysql8
记录一下安装过程用于后面项目参考 目录 说明安装步骤yum安装默认目录修改默认的数据目录必要的my.cnf属性修改卸载Mysql 说明 一般情况下都是docker安装,部分特殊情况下,例如老外的项目部分禁用docker,那一般二进制安装或者yum直接安装。 …...
Stable Diffusion使用教程:另一个线稿出3D例子)
十五)Stable Diffusion使用教程:另一个线稿出3D例子
案例:黄金首饰出图 1)线稿,可以进行色阶加深,不易丢失细节; 2)文生图,精确材质、光泽、工艺(抛光、拉丝等)、形状(包括深度等,比如镂空)和渲染方式(3D、素描、线稿等)提示词,负面提示词; 3)seed调-1,让ai随机出图; 4)开启controlnet,上传线稿图,选择cann…...
)
2023icpc网络预选赛I. Pa?sWorD(dp)
题目给定字符串长度n以及字符串s 其中出现小写字母可以代表小写字母和大写字母 比如a可以代表a和A 出现?可以代表26个小写字母和26个大写字母和10个数字 出现大写字母和数字就是原本的数 同时要求大写字母,小写字母,数字一定都存在替换完的字符串中…...

maven本地安装jar包
在实际开发中,有些jar包不能通过公共库下载,只能本地安装。可以按照以下步骤操作: 1、安装命令 mvn install:install-file -DgroupIdcom.chinacreator.sm -DartifactIdfbm-sm-common -Dversion0.0.1 -Dpackagingjar -Dfile../newJar/fbm-sm…...

QT中的inherits
目录 简介: 实例: 简介: 在Qt中,可以使用inherits函数来判断一个对象是否属于某个类或其派生类。inherits函数是QObject类的成员函数,因此只能用于继承自QObject的类的对象。 以下是inherits函数的一般用法…...
全国职业技能大赛云计算--高职组赛题卷①(容器云)
全国职业技能大赛云计算--高职组赛题卷①(容器云) 第二场次题目:容器云平台部署与运维任务1 Docker CE及私有仓库安装任务(5分)任务2 基于容器的web应用系统部署任务(15分)任务3 基于容器的持续…...
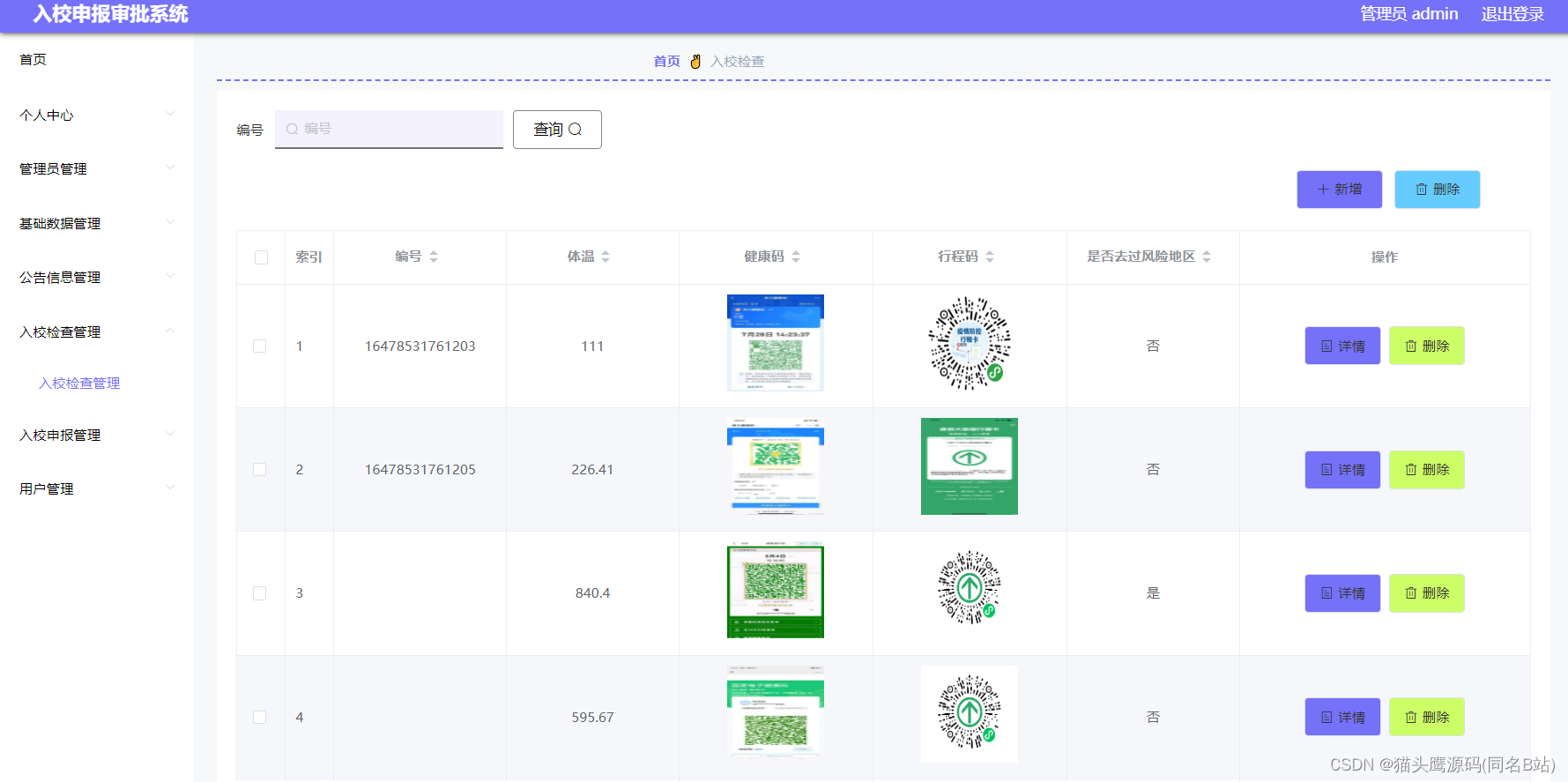
基于springboot+vue的入校申报审批系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

安卓逆向 - EdXposed LSPosed VirtualXposed
一、引言 接上篇:安卓逆向 - Xposed入门教程_小馒头yy的博客-CSDN博客 我们介绍了Xposed入门安装使用,但是只支持到Android 8,并且安装模块需要重启。今天我们来看看Xposed的其他版本。 二、各种Xposed框架对比 1、Xposed 只支持到安卓8&…...

Linux三大搜索指令的区别
find:可以在指定的路径下进行文件的搜索 —— 真的在磁盘文件中查找 例如find /usr/bin/ -name ls which 可以在指令路径下,/usr/bin,搜索指令文件 例如:which ls whereis:在系统特定的路径下查找,既可以找到可执行程序ÿ…...
C++ -- 特殊类设计
目录 设计一个类,不能被拷贝 C98的做法 C11的做法 设计一个类,只能在堆上创建对象 实现方式1 实现方式2 设计一个类,只能在栈上创建对象 实现方式1 方式1的优化 实现方式2 设计一个类,不能被继承 设计模式 什么是设计…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
