树哈希与换根dp:CF763D
采用的树哈希函数是:
d p x = w x × ∑ y ∈ x d p y 2 + w x 2 \Large dp_x=w_x\times \sum_{y\in x}dp_y^2+w_x^2 dpx=wx×y∈x∑dpy2+wx2
发现从 x x x 到 y y y 时只有 x x x 与 y y y 的哈希值会变化,分别维护即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 100010
//#define M
#define mo (int)(1e9+123)
int n, m, i, j, k, T;
int pos, mx, cnt, h[N], w[N], dp[N], f[N], u, v;
map<int, int>mp;
vector<int>G[N]; int Mod(int a) {return (a%mo+mo)%mo;
}void add(int x, int k) {mp[x]+=k; if(mp[x]==1 && k==1) ++cnt; if(mp[x]==0 && k==-1) --cnt;
// printf("# %lld (%lld): %lld\n", x, mp[x], cnt);
}void dfs1(int x, int fa) {
// int s1, s2=0; w[x]=1; for(int y : G[x]) {if(y==fa) continue; dfs1(y, x); w[x]+=w[y]; f[x]=Mod(f[x]+dp[y]*dp[y]); }dp[x]=Mod(w[x]*f[x]%mo+w[x]*w[x]%mo); add(dp[x], 1);
// printf("%lld : %lld\n", x, dp[x]);
}void dfs2(int x, int fa) {int xw, xf, xdp, yw, yf, ydp; for(int y : G[x]) {if(y==fa) continue;
// printf("del [%lld] : %lld\n", x, dp[x]); add(dp[x], -1); xdp=dp[x]; xw=w[x]; xf=f[x]; w[x]=w[x]-w[y]; f[x]=Mod(f[x]-dp[y]*dp[y]); dp[x]=(w[x]*f[x]%mo+w[x]*w[x]%mo);
// printf("ins [%lld] %lld : %lld\n", x, w[x], dp[x]); add(dp[x], 1); // printf("del [%lld] : %lld\n", y, dp[y]); add(dp[y], -1); ydp=dp[y]; yw=w[y]; yf=f[y]; w[y]=n; f[y]=Mod(f[y]+dp[x]*dp[x])%mo; dp[y]=(w[y]*f[y]%mo+w[y]*w[y]%mo); // printf("ins [%lld] : %lld\n", y, dp[y]); add(dp[y], 1); // printf("%lld : %lld\n", y, cnt);
// for(auto t=mp.begin(); t!=mp.end(); ++t) printf("%lld ", t); if(cnt>mx) mx=cnt, pos=y; dfs2(y, x); add(dp[x], -1); add(dp[y], -1); dp[x]=xdp; w[x]=xw; f[x]=xf; add(dp[x], 1); dp[y]=ydp; w[y]=yw; f[y]=yf; add(dp[y], 1); }
}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// T=read();
// while(T--) {
//
// }n=read(); for(i=1, k=1; i<n; ++i) {u=read(); v=read(); G[u].pb(v); G[v].pb(u); } dfs1(1, 0); mx=cnt; pos=1; dfs2(1, 0); printf("%lld", pos); return 0;
}相关文章:

树哈希与换根dp:CF763D
采用的树哈希函数是: d p x w x ∑ y ∈ x d p y 2 w x 2 \Large dp_xw_x\times \sum_{y\in x}dp_y^2w_x^2 dpxwxy∈x∑dpy2wx2 发现从 x x x 到 y y y 时只有 x x x 与 y y y 的哈希值会变化,分别维护即可 #include<bits/stdc.h&…...
npm、yarn、pnpm如何清除缓存?
前端工程化创建项目会经常使用各种安装包管理工具,安装各种前端依赖包。例如,npm、yarn、pnpm等。时间一长,各种安装包管理工具的在安装依赖时,留下的缓存文件就会变得很大,以至于影响系统的运行,因此必要时…...

12款最火的AI画图软件,助你探索创新设计
ChatGPT火爆出圈,AI画图软件也如雨后春笋般流行起来。各类AI画图的软件工具横空出世,设计师与其焦虑工作会不会被人工智能取代,不如践行“工欲善其事必先利其器”,开拓思路,打开格局,好好地探索下如何利用好…...
cookie信息无法获取问题研究
背景 在oneapi这个前后端都有的开源项目中,我想接入chatnextweb到oneapi的后端。 由于需要二开chatnextweb,添加登录注册功能,考虑到java后端的性能问题和内存占用,决定不重启写个服务,而是将登录注册接入到oneapi的…...
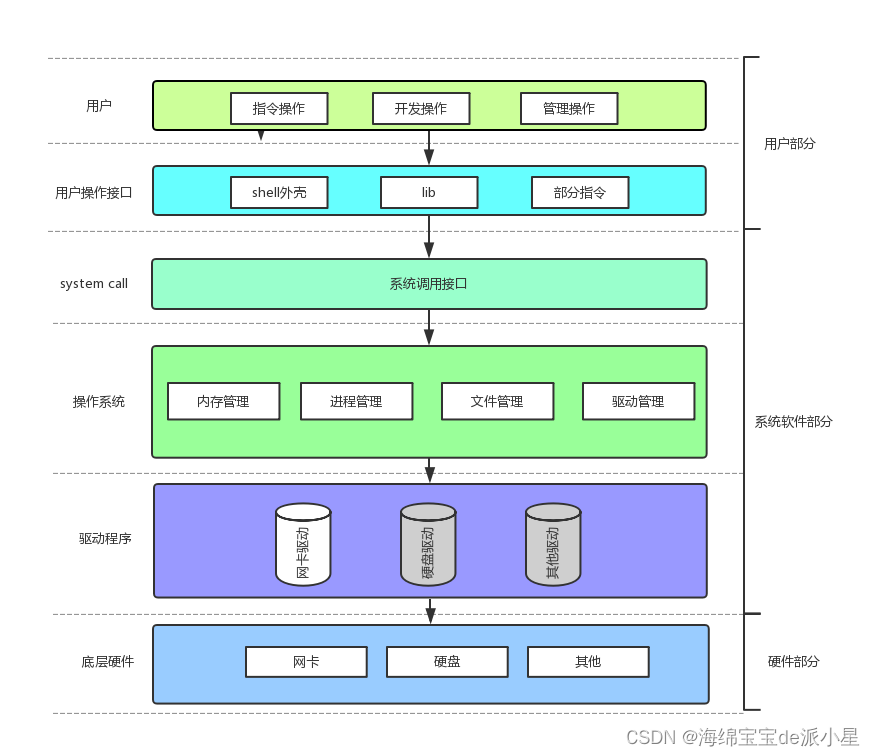
Linux:冯诺依曼系统和操作系统的概念
文章目录 冯诺依曼体系结构冯诺依曼体系的理解 操作系统操作系统的基本定位操作系统的理解1 操作系统的理解2总结 本篇主要总结的是操作系统的基本认知和一些概念 冯诺依曼体系结构 那么上图表示的就是冯诺依曼体系结构,那这个体系结构是什么?为什么要先…...
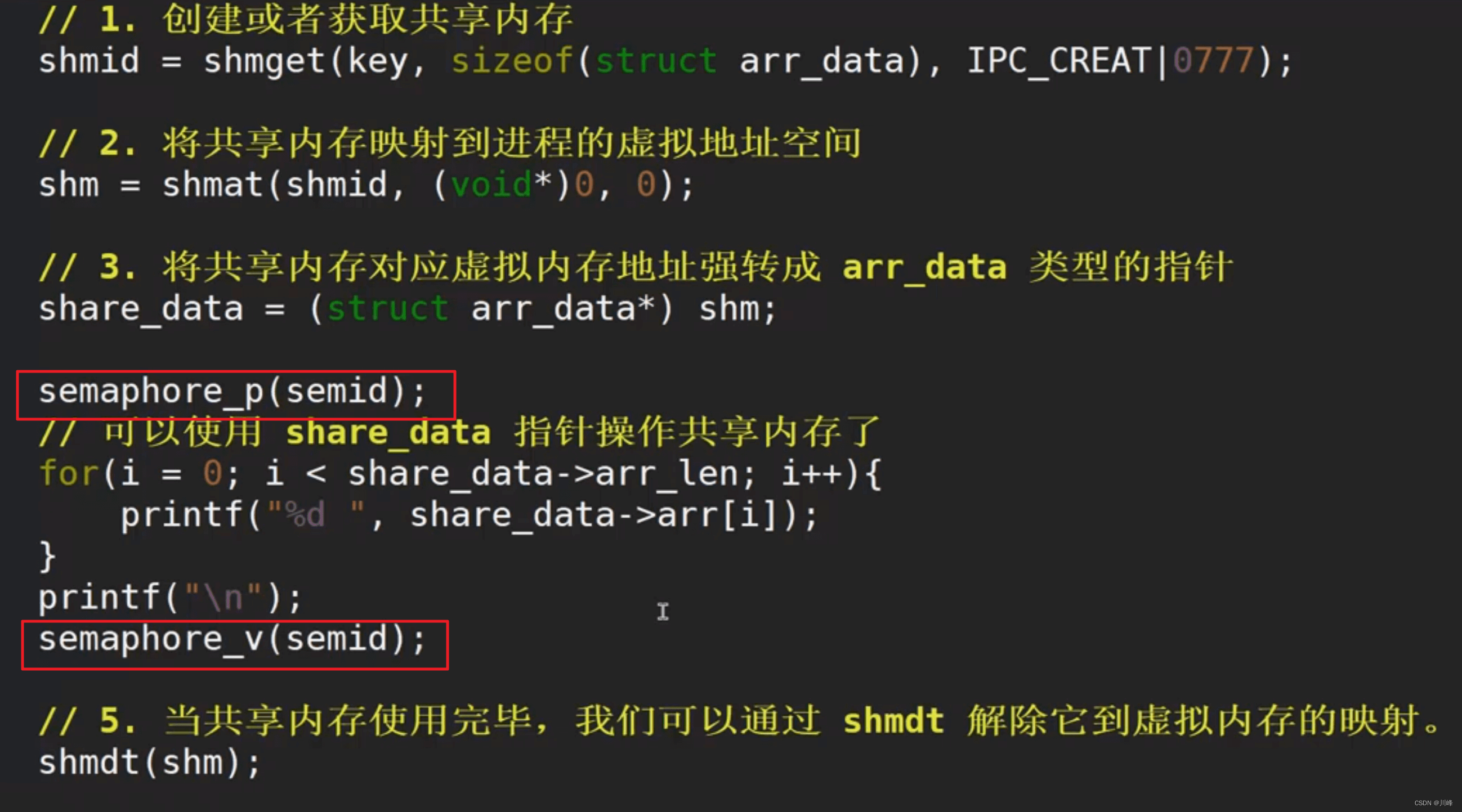
【操作系统笔记十一】进程间通信
Linux文件系统 inode 节点 (index node):给每个文件赋予一个称为 i 节点的数据结构。 inode 一开始是存储在硬盘中的,只有当文件被打开的时候,其对应的 i 节点才加载到内存中。 总结: Linux 中,…...

【操作系统】聊聊Linux软中断
什么是中断 中断是系统用来响应硬件设备请求的一种机制,会打断进程的正常调度和执行,转而去执行内核中的中断处理程序。 比如你正在看书,你女朋友叫你出去逛街。你就需要先放下手里的事情,然后逛街。回来之后,在接着看…...
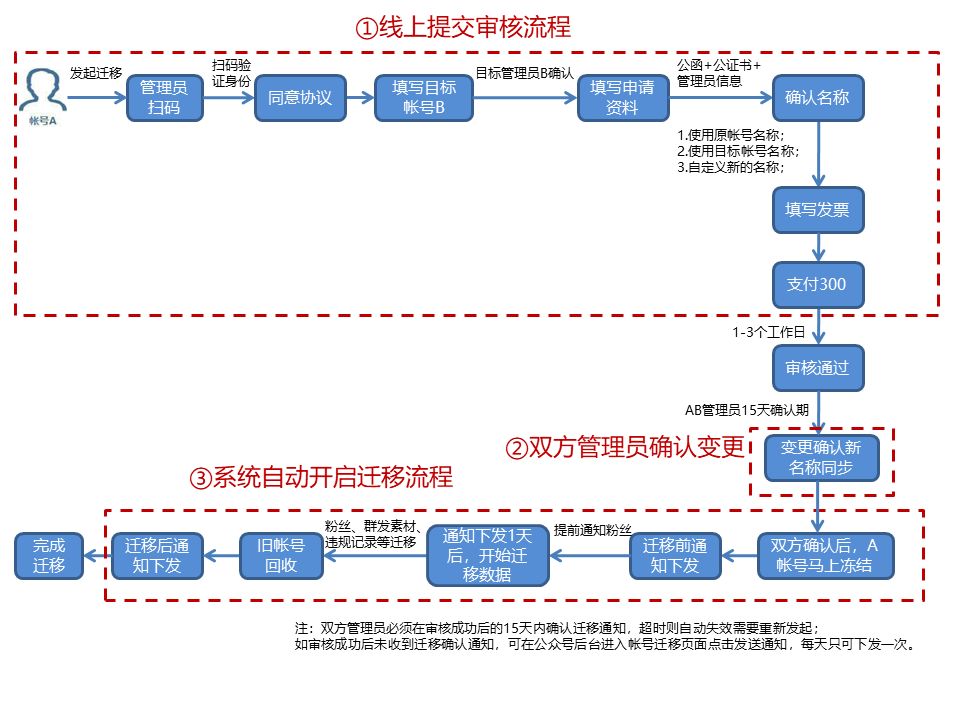
公众号迁移个人可以迁移吗?
公众号账号迁移的作用是什么?只能变更主体吗?很多小伙伴想做公众号迁移,但是不知道公众号迁移有什么作用,今天跟大家具体讲解一下。首先公众号迁移最主要的就是修改公众号的主体了,比如我们公众号原来是A公司的&#x…...
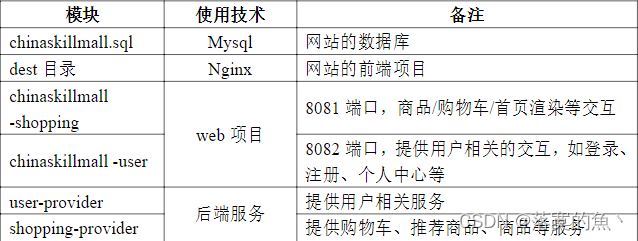
全国职业技能大赛云计算--高职组赛题卷⑤(容器云)
全国职业技能大赛云计算--高职组赛题卷⑤(容器云) 第二场次题目:容器云平台部署与运维任务2 基于容器的web应用系统部署任务(15分)任务3 基于容器的持续集成部署任务(15分)任务4 Kubernetes容器…...

支撑位和阻力位在Renko和烛台图如何使用?FPmarkets澳福3秒回答
很多投资者都知道,Renko图表和普通日本烛台都会采用相同的交易信号,即支撑位和阻力位。那么支撑位和阻力位在Renko和烛台图如何使用?FPmarkets澳福3秒回答。 这些信号在任何时间框架上都会出现,且在蜡烛图交易中颇受欢迎。对于Renko图表而言…...

如何在32位MCU用printf()函数打印64位数据
1. 在32位MCU上定义64位变量: unsigned long long time_base; unsigned long long temp_time;2. 调用打印函数: printf("RFID:time_base:%d\r\n",time_base); printf("RFID:temp_time:%d\r\n",temp_time); printf("RFID:Ru…...

Python爬虫程序设置代理常见错误代码及解决方法
Python爬虫程序设置代理是爬虫程序中常用的技巧,可以有效地绕过IP限制,提高爬虫程序的稳定性和效率。然而,在设置代理时,常会出现各种错误代码,这些错误代码可能会影响程序的正常运行,甚至导致程序崩溃。本…...

3D点云目标检测:Centerformer训练waymo数据集
一、环境准备 项目地址:centerformer 1.0、基础环境 python 3.8.0 torch 1.9.1cu111 waymo-open-dataset-tf-2-6-0 1.4.9 spconv 1.2.1 其余按照requirement.txt里安装就行 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple -r requirements.txt由于我本人是在…...
火山引擎DataLeap推出两款大模型应用: 对话式检索与开发 打破代码语言屏障
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 自上世50年代,以“计算机”作为代表性象征的信息革命开始,社会对于先进生产力的认知便开始逐步更迭——从信息化(通常认为是把企…...
windows上配置vscode C/C++代码跳转
windows上配置vscode C/C代码跳转 安装插件 C/C 官方的 C/C 插件,必备的插件,是代码跳转、自动补全、代码大纲显示等功能的基础。 Gtags C/C GNU Global GNU Global除了安装该插件之外,还需要在本地下载安装GNU Global工具。多看下插件…...
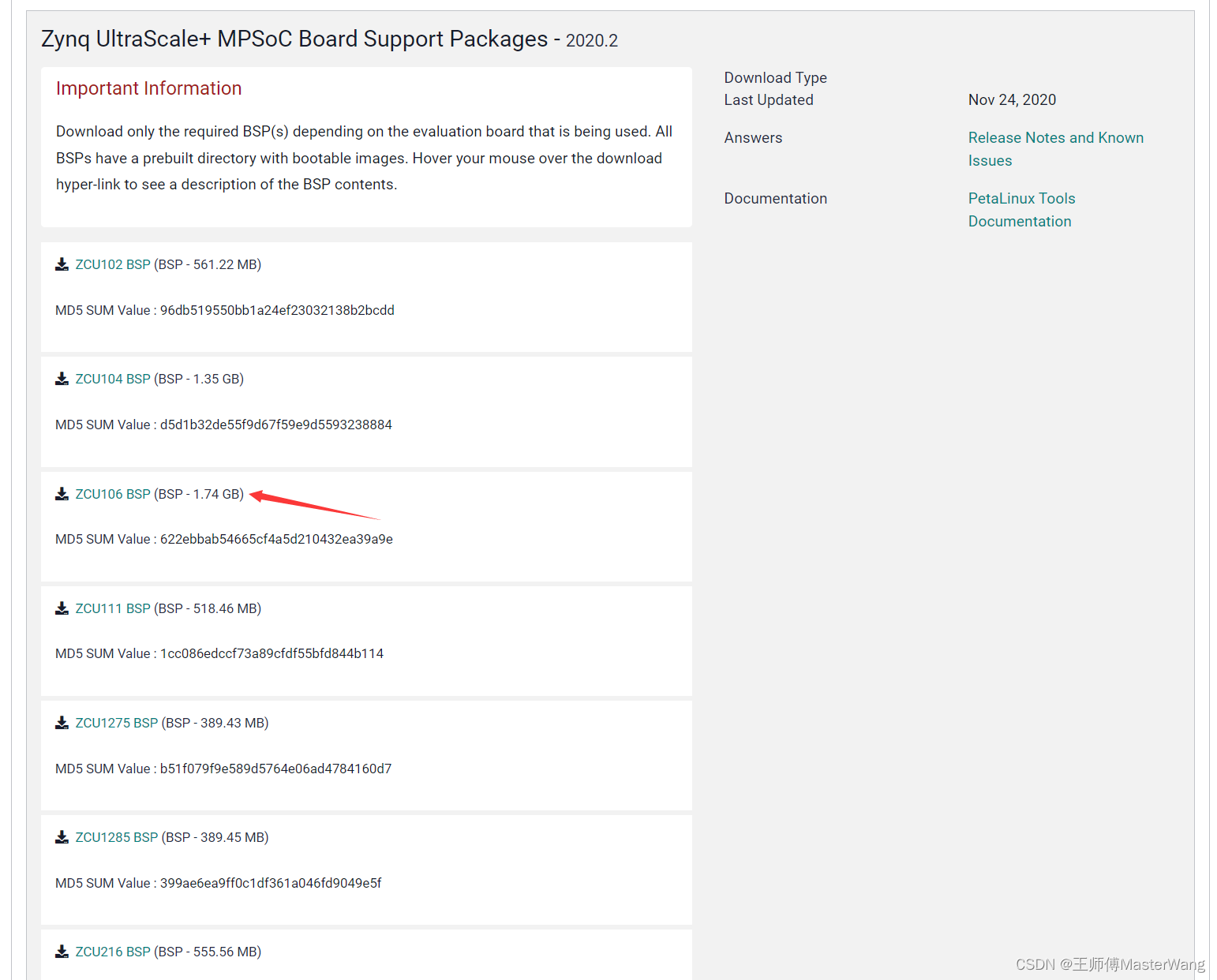
【Xilinx】基于MPSoC的OpenAMP实现(一)
【Xilinx】基于MPSoC的OpenAMP实现(一) 一、开发环境1、开发思路2、下载官方bsp包 二、编译Linux1、配置petalinux环境变量2、创建工程3、进入目录4、设置缓存目录(重点:可离线编译,加快编译速度)5、配置u-…...
代码随想录算法训练营总结篇|完结撒花
完结撒花,真不敢相信60天坚持下来了。 算法一直是我的超级超级弱项,属于小白中的小白。一开始是想自己刷的,打开leetcode第一题,吼哟好家伙,梦开始的地方直接破碎。之前刷B站的时候就有学习up推荐算法可以看看代码随想…...
uniapp、vue实现滑动拼图验证码
uniapp、vue实现滑动拼图验证码 实际开发工作中,在登陆的时候需要短信验证码,但容易引起爬虫行为,需要用到反爬虫验证码,今天介绍一下拼图验证码,解决验证码反爬虫中的滑动验证码反爬虫。滑动拼图验证码是在滑块验证码…...

【ArcGIS】土地利用变化分析详解(矢量篇)
土地利用变化分析详解-矢量篇 土地利用类型分类1 统计不同土地利用类型的面积/占比1.1 操作步骤Step1:Step2:计算面积Step3:计算占比 2 统计不同区域各类土地利用类型的面积2.1 操作步骤 3 土地利用变化转移矩阵3.1 研究思路3.2 操作步骤 4 分…...
VS2022创建控制台应用程序后没有Main了,如何显示Main?
文章目录 问题描述原因解决方案简单的顶级语句试用计算器 其他文章 问题描述 用VS2022创建一个控制台应用后,没有名称空间和Main函数了,只有一个WriteLine,如下所示。 // See https://aka.ms/new-console-template for more information Co…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
