怒刷LeetCode的第12天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:贪心
第二题
题目来源
题目内容
解决方法
方法一:双指针
方法二:KMP算法
方法三:indexOf方法
方法四:Boyer-Moore算法
方法五:Rabin-Karp算法
第三题
题目来源
题目内容
解决方法
方法一:递减法
方法二:位运算和循环
方法三:二分查找
第一题
题目来源
2591. 将钱分给最多的儿童 - 力扣(LeetCode)
题目内容

解决方法
方法一:贪心
class Solution {public int distMoney(int money, int children) {// 如果可分配的钱小于儿童的个数,则无法均分,返回-1if (money < children) {return -1;}// 减去每个儿童至少分配的1美元后剩余的钱money -= children;// 计算剩下的钱最多可以再均分给多少个儿童,即money / 7与儿童个数中的较小值int cnt = Math.min(money / 7, children);// 已经分配了cnt个儿童money -= cnt * 7;children -= cnt;// 如果剩余的儿童个数为0且剩余的钱大于0,或者剩余的儿童个数为1且剩余的钱为3// 表示不满足要求,需要减少已分配的儿童个数if ((children == 0 && money > 0) || (children == 1 && money == 3)) {cnt--;}// 返回已分配的儿童个数return cnt;}
}
这段代码是使用贪心思路实现的,计算分配钱币给儿童的最多个数。
- 如果总钱数小于儿童个数,无法进行分配,返回-1。
- 将每个儿童至少获得1美元后,将剩余的钱数money减去儿童个数。
- 计算可以获得7美元的儿童个数,最多为儿童个数和money/7的较小值。
- 将7美元的儿童个数乘以7减去money,得到剩余要分配的钱数。
- 剩余的儿童个数等于总儿童个数减去7美元的儿童个数。
- 如果剩余的儿童个数为0且还有剩余的钱,则将7美元的儿童个数减1。
- 返回最终的儿童个数。
复杂度分析:
- 时间复杂度为O(1),因为无论输入的数值大小如何,都只需要执行固定数量的操作。具体而言,算法中只有一些简单的数学运算和比较,没有使用循环或递归等可变的迭代结构。
- 空间复杂度也为O(1),因为算法中没有使用额外的数据结构来存储数据,只是使用了几个变量来保存中间结果。
LeetCode运行结果:
第二题
题目来源
28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
题目内容

解决方法
方法一:双指针
- 首先判断 needle 是否为空字符串,如果是则直接返回 0。然后判断 haystack 的长度是否小于 needle 的长度,如果是则不可能匹配,返回 -1。
- 接着使用两个指针 i 和 j 分别指向 haystack 和 needle 的起始位置,通过一个循环遍历 haystack 字符串。在循环中,使用 j 来遍历 needle 字符串,如果匹配失败,则退出当前循环,将 i 后移一个位置。
- 如果在遍历 j 结束时,j 的值等于 needle 的长度 n,说明找到了匹配项,返回 i 的值即可。
- 如果循环结束后仍然没有找到匹配项,则返回 -1。
class Solution {public int strStr(String haystack, String needle) {int m = haystack.length();int n = needle.length();// 如果 needle 为空字符串,则返回 0if (n == 0) {return 0;}// 如果 haystack 长度小于 needle 长度,则不可能匹配,返回 -1if (m < n) {return -1;}for (int i = 0; i <= m - n; i++) {int j;// 在 haystack 中从当前位置开始与 needle 进行匹配for (j = 0; j < n; j++) {if (haystack.charAt(i + j) != needle.charAt(j)) {break;}}// 如果 j 的值等于 needle 的长度,则说明找到了匹配项,返回匹配项的下标if (j == n) {return i;}}// 没有找到匹配项,返回 -1return -1;}
}
复杂度分析:
- 时间复杂度:在最坏情况下,需要遍历 haystack 的每个字符,并且在每个位置进行 needle 的匹配。因此,时间复杂度为 O((m-n+1) * n),其中 m 是 haystack 的长度,n 是 needle 的长度。注意,这里的 (m-n+1) 是遍历的次数,每次遍历都需要比较 n 个字符。
- 空间复杂度:代码中只使用了常数个变量,因此空间复杂度为 O(1)。
需要注意的是,虽然上述代码的时间复杂度与 needle 的长度 n 相关,但由于 n 的取值范围很小(1 <= n <= 104),因此该算法在实际情况中通常会表现良好。
LeetCode运行结果:
方法二:KMP算法
当使用KMP算法来实现字符串匹配时,需要先构建Next数组,然后利用Next数组进行匹配。
class Solution {
public int strStr(String haystack, String needle) {if (needle.isEmpty()) {return 0;}int[] next = getNext(needle);int i = 0, j = 0, m = haystack.length(), n = needle.length();while (i < m) {if (haystack.charAt(i) == needle.charAt(j)) {i++;j++;if (j == n) {return i - j;}} else if (j > 0) {j = next[j - 1];} else {i++;}}return -1;}private static int[] getNext(String pattern) {int[] next = new int[pattern.length()];int i = 1, j = 0, n = pattern.length();while (i < n) {if (pattern.charAt(i) == pattern.charAt(j)) {j++;next[i] = j;i++;} else if (j > 0) {j = next[j - 1];} else {next[i] = 0;i++;}}return next;}
}以上代码中,strStr方法用于进行字符串匹配,返回第一个匹配位置的索引(若不存在匹配则返回-1)。getNext方法用于构建模式串(即 needle)的Next数组。
复杂度分析:
KMP算法的时间复杂度为O(m+n),其中m为原串的长度,n为模式串的长度。
- getNext方法的时间复杂度是O(n),因为需要依次计算Next数组中每一个元素的值。
- strStr方法的时间复杂度是O(m),因为需要依次遍历原串中的每一个字符。在最坏情况下(即当原串中不存在匹配子串时),strStr方法的时间复杂度为O(m-n+1),即O(m)。
综上所述,KMP算法的时间复杂度为O(m+n)。空间复杂度为O(n),即Next数组的长度。
需要注意的是,KMP算法虽然能够提高字符串匹配的效率,但也有一定的局限性。当模式串过长时,构建Next数组的时间可能会变得很慢,从而影响整个算法的性能。
LeetCode运行结果:
方法三:indexOf方法
可以使用Java中的indexOf方法来实现。indexOf方法用于查找子字符串在父字符串中第一次出现的位置。
class Solution {public int strStr(String haystack, String needle) {return haystack.indexOf(needle);}
}
在上述代码中,strStr方法接受两个参数haystack和needle,并调用indexOf方法在haystack字符串中查找needle字符串的第一次出现位置。如果找到了匹配项,则返回对应的下标;否则,返回-1。
复杂度分析:
- 时间复杂度:该算法使用Java中的indexOf方法,其时间复杂度为O((n-m+1)m),其中n为haystack字符串的长度,m为needle字符串的长度。具体来说,在最坏情况下,需要遍历haystack的每个字符,并检查是否与needle相等,因此时间复杂度为O((n-m+1)m)。
- 空间复杂度:该算法的空间复杂度为O(1),因为只使用了常数级别的额外空间。
需要注意的是,尽管indexOf方法的时间复杂度为O((n-m+1)m),但在实际应用中,它通常比手动实现的算法更高效。这是因为indexOf方法在底层经过了优化,使用了一些技巧来加速字符串匹配。因此,在大多数情况下,使用现有的API是更好的选择。当然,如果需要特定的定制功能或特别高效的性能,可能需要考虑实现自己的匹配算法。
LeetCode运行结果:
方法四:Boyer-Moore算法
Boyer-Moore算法利用了两个启发式规则来跳过尽可能多的字符,以达到快速匹配的目的。这两个规则是坏字符规则(Bad Character Rule)和好后缀规则(Good Suffix Rule)。
class Solution {
public int strStr(String haystack, String needle) {int n = haystack.length();int m = needle.length();if (m == 0) {return 0;}int[] badChar = new int[256];Arrays.fill(badChar, -1);for (int i = 0; i < m; i++) {badChar[needle.charAt(i)] = i;}int s = 0;while (s <= n - m) {int j = m - 1;while (j >= 0 && needle.charAt(j) == haystack.charAt(s + j)) {j--;}if (j < 0) {return s;} else {s += Math.max(1, j - badChar[haystack.charAt(s + j)]);}}return -1;
}}
在该代码中,我们首先对needle字符串进行预处理,得到坏字符表badChar,其中badChar[c]表示字符c在needle中最靠右出现的位置,如果字符c不在needle中,则为-1。
然后,我们从0开始枚举haystack中长度为m的子串s,并比较s与needle是否相等。如果相等,则返回当前起始位置;否则,我们利用坏字符表来计算s需要移动的距离。
具体来说,我们将字串s中最靠右的坏字符与s中的对应字符对齐,然后向右移动j - badChar[haystack.charAt(s + j)]个字符,其中j - badChar[haystack.charAt(s + j)]表示坏字符在needle中最靠右出现的位置与它在s中出现的位置之差。如果坏字符不在子串s中,则我们可以将s直接向右移动一个位置。
复杂度分析:
- Boyer-Moore算法的时间复杂度为O(n+m),其中n是haystack字符串的长度,m是needle字符串的长度。在主循环中,我们通过比较needle和子串s的最后一个字符来判断是否匹配。如果不匹配,我们利用坏字符表badChar来计算需要移动的距离。在最坏情况下,每次比较都有一个字符不匹配,那么主循环的迭代次数为O(n/m)。而在每次比较中,通过坏字符表找到需要移动的距离的时间复杂度为O(m)。所以总体的时间复杂度为O(n/m * m) = O(n)。
- 空间复杂度方面,除了输入字符串之外,我们只使用了一个大小为256的数组badChar来存储坏字符表,因此空间复杂度为O(1)。
值得注意的是,Boyer-Moore算法的性能在处理大文本时更加明显,因为它利用了预处理表格来跳过尽可能多的字符,减少了比较的次数。
总结起来,Boyer-Moore算法是一种高效的字符串匹配算法,适用于处理大文本的情况,时间复杂度为O(n+m),空间复杂度为O(1)。
LeetCode运行结果:
方法五:Rabin-Karp算法
Rabin-Karp算法的基本思想是通过计算字符串的hash值来进行快速匹配。具体步骤如下:
1、首先,判断特殊情况,如果needle为空字符串,则返回0;如果haystack的长度小于needle的长度,则返回-1。
2、接下来,计算needle和haystack的初始hash值。这里使用了一个质数31作为base,并将每个字符映射为对应的整数值。
- 初始化needleHash和currHash为0,用于存储hash值。
- 初始化power为1,用于在滑动窗口时快速计算hash值。
3、然后,使用一个循环遍历needle的每个字符,计算needleHash和currHash,并更新power的值。
4、然后,在一个循环中,通过滑动窗口的方式在haystack上逐个移动子串,并比较hash值是否相等和子串是否与needle相同。
- 如果当前hash值相等并且子串与needle相同,则返回子串在haystack中的起始位置。
- 如果当前hash值不相等,通过重新计算hash值的方式继续滑动窗口。
5、如果循环结束后仍未找到匹配,返回-1表示未找到。
class Solution {
public int strStr(String haystack, String needle) {int n = haystack.length();int m = needle.length();if (m == 0) {return 0;}if (n < m) {return -1;}int prime = 31;long needleHash = 0;long currHash = 0;long power = 1;for (int i = 0; i < m; i++) {needleHash = needleHash * prime + (needle.charAt(i) - 'a');currHash = currHash * prime + (haystack.charAt(i) - 'a');power *= prime;}for (int i = 0; i <= n - m; i++) {if (currHash == needleHash && haystack.substring(i, i + m).equals(needle)) {return i;}if (i < n - m) {currHash = currHash * prime - (haystack.charAt(i) - 'a') * power + (haystack.charAt(i + m) - 'a');}}return -1;
}}复杂度分析:
- 哈希值计算:计算模式串和文本串中第一个子串的哈希值,需要遍历模式串和子串的字符。因此,哈希值计算的时间复杂度为O(m),其中m为模式串的长度。
- 哈希值比较:在每次哈希值匹配的情况下,需要比较模式串和当前子串是否相等。最坏情况下,需要比较所有字符,时间复杂度为O(m)。
- 滑动窗口:滑动窗口的操作需要在文本串上移动,移动n - m + 1次,其中n是文本串的长度,m是模式串的长度。每次滑动窗口需要进行哈希值计算和哈希值比较操作,时间复杂度为O(1)。
综上所述,Rabin-Karp算法的总体时间复杂度为O((n-m+1) * m),其中n是文本串的长度,m是模式串的长度。在最坏情况下,即当哈希值匹配每次都发生冲突时,时间复杂度可能达到O(nm)。
需要注意的是,选择合适的哈希函数和哈希值比较算法对算法的性能有影响。另外,Rabin-Karp算法需要额外的空间来存储哈希值,空间复杂度为O(m)。
LeetCode运行结果:
第三题
题目来源
29. 两数相除 - 力扣(LeetCode)
题目内容

解决方法
方法一:递减法
- 首先,处理特殊情况。如果被除数为0,则返回0;如果除数为1,则返回被除数本身。
- 接下来,处理除数为-1的情况。如果被除数大于Integer.MIN_VALUE,说明除法结果不会溢出,直接返回被除数的相反数;否则,返回Integer.MAX_VALUE,避免溢出。
- 处理正负号。通过判断被除数和除数的符号,确定最终结果的符号。
- 将被除数和除数都转为正数进行计算。
- 使用循环逐步减去除数,每次循环都将除数翻倍,同时记录除数的倍数,即为商。
- 循环结束后,根据步骤3中记录的符号,返回正确的商。
- 最后,检查商是否溢出。如果超过了Integer.MAX_VALUE,则返回Integer.MAX_VALUE。
class Solution {
public int divide(int dividend, int divisor) {// 处理边界条件if (dividend == 0) { // 被除数为0return 0;}if (divisor == 1) { // 除数为1return dividend;}if (divisor == -1) { // 除数为-1if (dividend > Integer.MIN_VALUE) { // 检查是否溢出return -dividend;} else {return Integer.MAX_VALUE;}}// 处理正负号boolean isNegative = (dividend < 0 && divisor > 0) || (dividend > 0 && divisor < 0);// 将被除数和除数都转为正数进行计算long dividendAbs = Math.abs((long) dividend);long divisorAbs = Math.abs((long) divisor);int quotient = 0;while (dividendAbs >= divisorAbs) {long temp = divisorAbs;int multiple = 1; // 除数的倍数while (dividendAbs >= (temp << 1)) {temp <<= 1;multiple <<= 1;}dividendAbs -= temp;quotient += multiple;}if (isNegative) {quotient = -quotient;}// 检查是否溢出if (quotient > Integer.MAX_VALUE) {return Integer.MAX_VALUE;} else {return quotient;}
}}复杂度分析:
- 处理边界条件的操作是O(1),它们只需要执行一次。
- 处理正负号的操作是O(1),它只需要进行一次比较和赋值操作。
- 将被除数和除数转为正数的操作是O(1),它只需要调用Math.abs()方法一次。
- 主要的计算过程是通过一个while循环实现的。在每次循环中,除数会翻倍,因此总共进行的迭代次数不会超过log(N),其中N是被除数与除数的差值的大小。
- 在每次循环中,判断被除数与除数的大小关系、减去除数、更新商等操作都是O(1)的。
综上所述,代码的时间复杂度主要由循环的迭代次数决定,即O(logN)。其中N是被除数与除数的差值的大小。空间复杂度方面,代码只使用了有限的变量存储中间结果,所以是O(1)的。
需要注意的是,由于代码使用了long类型来处理可能的溢出情况,因此在某些情况下,时间复杂度可能会略微增加,具体取决于具体的输入值。但整体上,该算法的时间复杂度仍然是O(logN)的。
LeetCode运行结果:
方法二:位运算和循环
思路是使用位运算和循环来实现整数相除的操作。
- 首先,我们先处理一些特殊情况。如果除数为0,或者被除数为最小值且除数为-1(防止溢出),那么返回Integer.MAX_VALUE作为结果。
- 然后,我们判断结果的符号。如果被除数和除数的符号不同,那么商的符号为负;否则为正。
- 接下来,我们将被除数和除数都转为正数进行计算,防止溢出。使用long类型的变量来保存转换后的值。
- 然后,我们通过循环来不断减去除数,直到被除数小于除数为止。在每次循环中,我们使用位运算将除数扩大两倍(左移一位),并记录扩大的倍数。当被除数小于等于扩大后的除数时,我们将被除数减去扩大后的除数,并将倍数累加到结果中。
- 最后,根据之前判断的符号,确定结果的正负,并返回结果。
class Solution {
public int divide(int dividend, int divisor) {// 判断特殊情况:除数为0、被除数为最小值且除数为-1(防止溢出)if (divisor == 0 || (dividend == Integer.MIN_VALUE && divisor == -1)) {return Integer.MAX_VALUE;}// 判断结果的符号boolean negative = (dividend < 0) ^ (divisor < 0);// 将被除数和除数都转为负数进行计算,防止溢出long dvd = Math.abs((long) dividend);long dvs = Math.abs((long) divisor);int result = 0;while (dvd >= dvs) {long temp = dvs;long multiple = 1;while (dvd >= (temp << 1)) {temp <<= 1;multiple <<= 1;}dvd -= temp;result += multiple;}// 根据符号确定结果的正负if (negative) {return -result;} else {return result;}
}}复杂度分析:
- 时间复杂度:主要集中在两个循环中。外层循环中,每次被除数减去扩大的除数,直到被除数小于除数为止,所需的迭代次数最多为被除数和除数的差值的二进制位数。内层循环中,通过位运算将除数不断左移,直到大于被除数的一半。因此,总体时间复杂度为O(log(max(dividend, divisor)))。
- 空间复杂度:算法只使用了常数级别的额外空间,主要是用于存储一些变量和结果。因此,空间复杂度为O(1)。
需要注意的是,在处理边界情况时,判断除数是否为0以及被除数为最小值且除数为-1等操作都是常数级别的操作,并不会改变算法的时间和空间复杂度。
综上所述,该算法的时间复杂度为O(log(max(dividend, divisor))),空间复杂度为O(1)。
LeetCode运行结果:
方法三:二分查找
使用了二分查找的思想,通过不断将搜索范围缩小来逼近商的值,直到找到最接近的商。
具体实现步骤如下:
- 对特殊情况进行处理,当被除数为 Integer.MIN_VALUE 且除数为 -1 时,由于计算过程中会出现溢出,因此要返回 Integer.MAX_VALUE。
- 将被除数和除数转换为长整型,避免计算过程中出现溢出。
- 确定搜索的上下界,左边界为 0,右边界为被除数。
- 进行二分查找,在每次查找过程中,先计算中间值 mid,然后判断 mid * dvs 是否小于等于 dvd,如果是,则将 res 更新为 mid,同时将左边界 left 更新为 mid + 1,以继续向右侧搜索;否则,说明 mid * dvs 大于 dvd,需要向左侧搜索,将右边界 right 更新为 mid - 1。
- 当左右边界相遇时,二分查找结束,返回 res 作为商的结果。根据被除数和除数的符号,可以通过异或运算来确定商的符号。
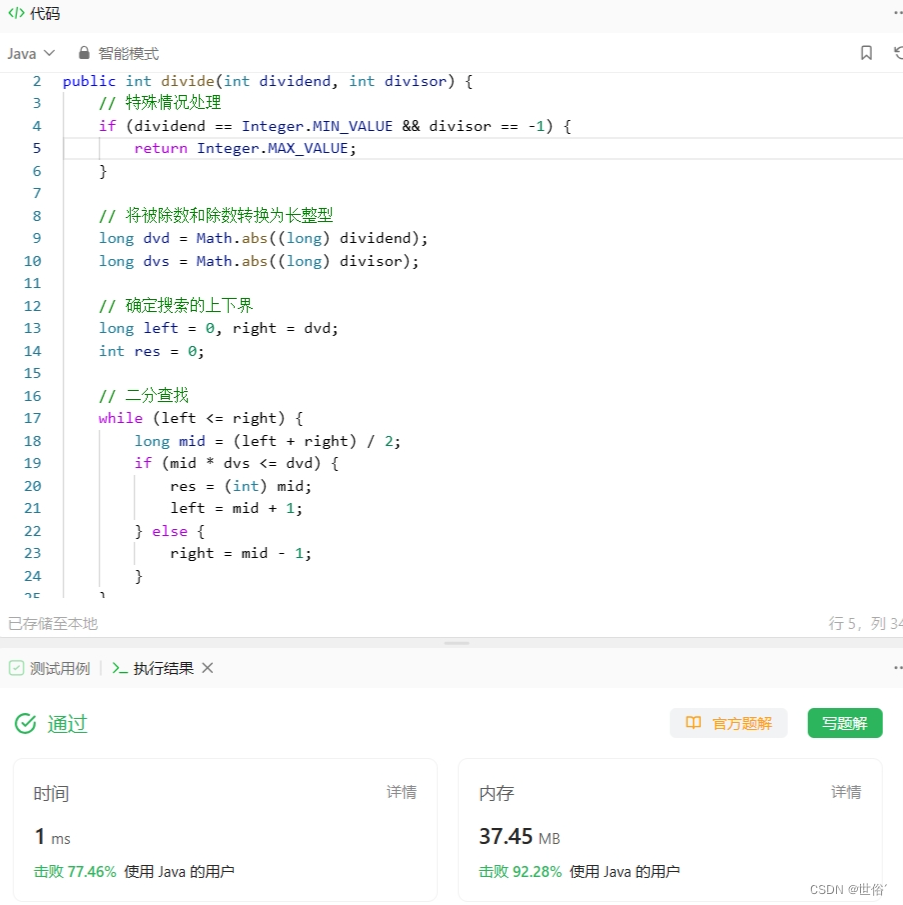
class Solution {
public int divide(int dividend, int divisor) {// 特殊情况处理if (dividend == Integer.MIN_VALUE && divisor == -1) {return Integer.MAX_VALUE;}// 将被除数和除数转换为长整型long dvd = Math.abs((long) dividend);long dvs = Math.abs((long) divisor);// 确定搜索的上下界long left = 0, right = dvd;int res = 0;// 二分查找while (left <= right) {long mid = (left + right) / 2;if (mid * dvs <= dvd) {res = (int) mid;left = mid + 1;} else {right = mid - 1;}}// 根据符号返回结果return ((dividend > 0) ^ (divisor > 0)) ? -res : res;
}}复杂度分析:
- 时间复杂度:使用二分查找的思路,每次查找可以将搜索范围缩小为原来的一半,因此时间复杂度为 O(logN),其中 N 是被除数除以除数的结果。
- 空间复杂度:该方法只定义了几个基本类型变量,所以空间复杂度是常数级别的,即 O(1)。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第12天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:贪心 第二题 题目来源 题目内容 解决方法 方法一:双指针 方法二:KMP算法 方法三:indexOf方法 方法四:Boyer-Moore算法 方法五:Rabin-Karp算法…...
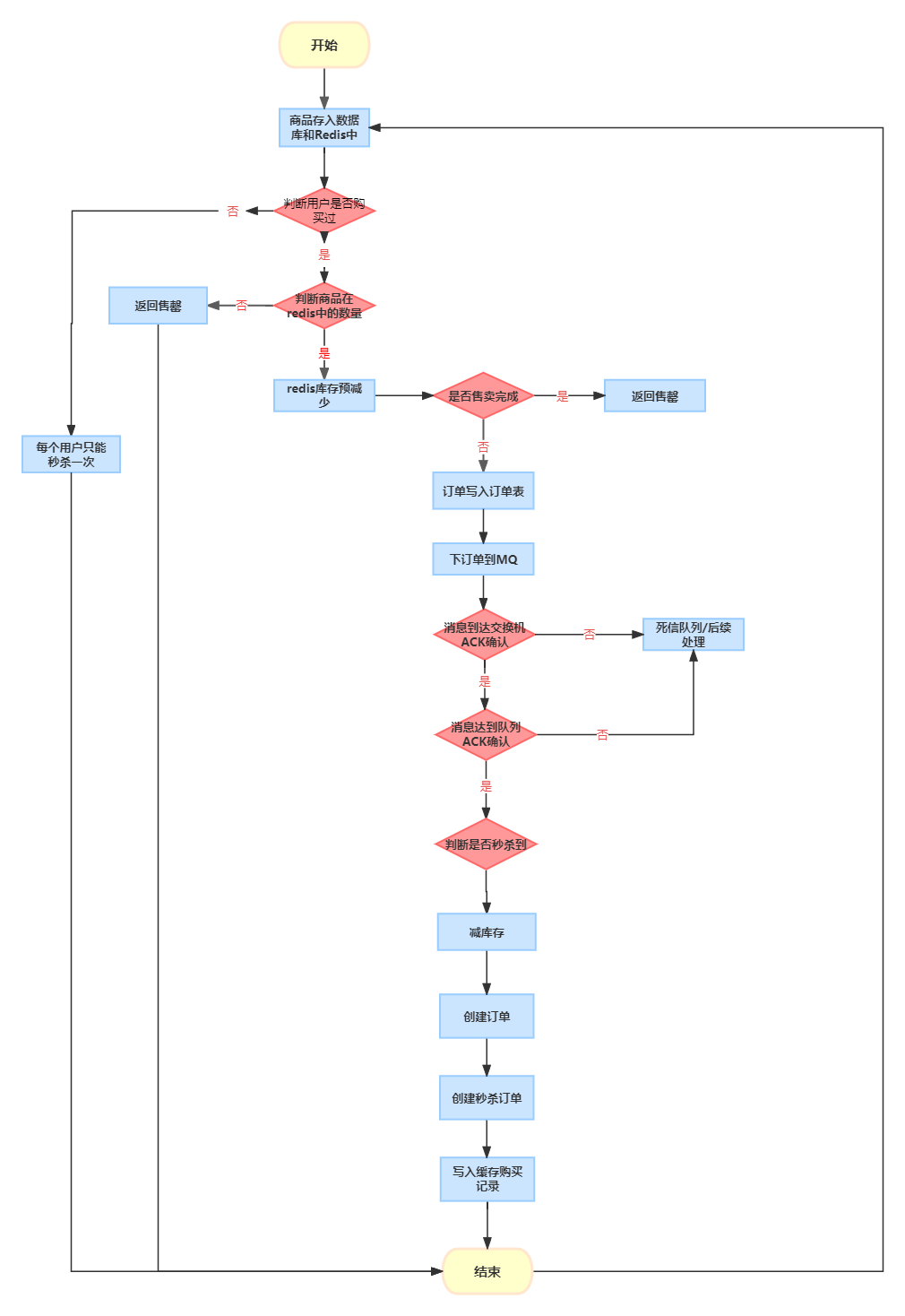
RabbitMQ实现秒杀场景示例
本文章通过MQ队列来实现秒杀场景 整体的设计如下图,整个流程中对于发送发MQ失败和发送到死信队列的数据未做后续处理 1、首先先创建MQ的配置文件 Configuration public class RabbitConfig {public static final String DEAD_LETTER_EXCHANGE "deadLetterE…...

如何提升网站排名优化(百度SEO优化,轻松提升排名)
在当今互联网时代,拥有一个优秀的网站是很重要的。而一个网站如果能够在搜索引擎上的排名很靠前,那么将会带来更多的流量、更多的用户和更多的利润。那么如何提升网站排名优化呢?蘑菇号www.mooogu.cn 百度SEO优化的5个规则 1.关键词选取要合…...

CountDownLatch 和 CyclicBarrier 用法以及区别
在使用多线程执行任务时,通常需要在主线程进行阻塞等待,直到所有线程执行完毕,主线程才能继续向下执行,主要有以下几种可选方式 1. 调用 main 线程的 sleep 方法 一般用于预估线程的执行时间,在主线程内执行线程sleep…...
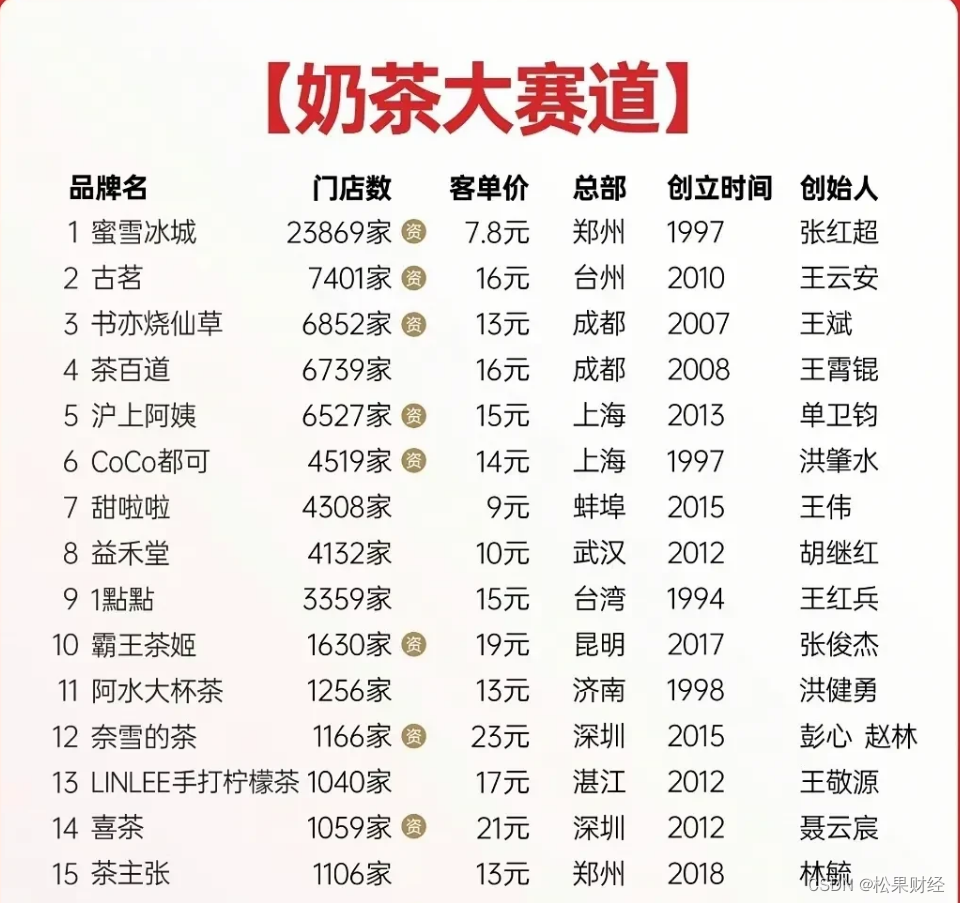
9.9喝遍“茶、奶、果、酒”,茶饮价格战是因为“无活可整”?
“家人们谁懂啊,周一瑞幸周二奈雪周三茶百道周四库迪周五古茗周六coco,9块9根本喝不完!” 紧随咖啡的9.9大战,茶饮们也在今年加速“蜜雪冰城化”,9.9变成了一种潮流。伴随着茶百道、coco、奈雪的茶等品牌把9.9玩出了更…...

echarts 学习网址
1、PPChart 网址:PPChart - 让图表更简单 2、YX-Chartlib 网址:http://chartlib.datains.cn3、isqqw 网址:echarts图表集4、makeapie 网址:makeapie echarts社区图表可视化案例5、Chart.Top 网址:chart.top - 让图…...

android源码编译
整包编译 导入环境变量 source ./build/envsetup.shlunch:选择平台编译选项make:执行编译 编译单个apk 进入到apk mk所在路径 mma...

盘点双电机驱动技术
对于电动汽车来说,双电机相对于单电机加主减速器或变速箱的方案在提高驱动效率方面的优势: 第一,单电机在低速、高速轻载等情况下,效率降低比较严重。 电动机的高效区间虽然比内燃机大得多,但是汽车的转速和转矩要求…...

ubuntu下用pycharm专业版连接AI服务器及其docker环境
一:用pycharm专业版连接AI服务器 1、首先在自己电脑上新建一个文件夹,后续用于映射服务器上自己所要用的项目文件 2、用pycharm专业版打开该文件夹,作为一个项目打开 3、然后在工具->部署->配置 4、配置中形式如下: 点击左…...

IntentFilter笔记
一、action <intent-filter>中可以有多个action,Intent只要匹配其中1个action即匹配成功<intent-filter>没有action,任何Intent无法与之匹配<intent-filter>中有action,Intent中没有action时可以与之匹配成功<intent-fi…...
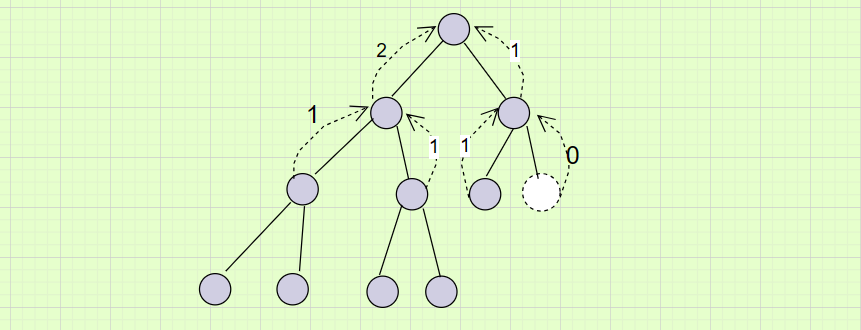
【二叉树】——链式结构(快速掌握递归与刷题技巧)
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...

项目管理—项目普遍存在的问题
软件公司有开发业务,在完成一个软件产品或实施项目时,常常会出现以下的状况: 开发人员不懂客户业务,一个高大上的规划,落地后的软件,只是机械的满足了基本功能,毫无易用性和科学性可言。 项目只…...

Ubuntu Seata开机自启动服务
1、创建service文件 在/lib/systemd/system目录下创建seata.service文件 [Unit] Descriptionalibaba seata Afternetwork.target Documentationhttps://seata.io/zh-cn/[Service] Userroot Grouproot Typeforking Environment"JAVA_HOME/usr/local/programs/jdk-8u333-li…...
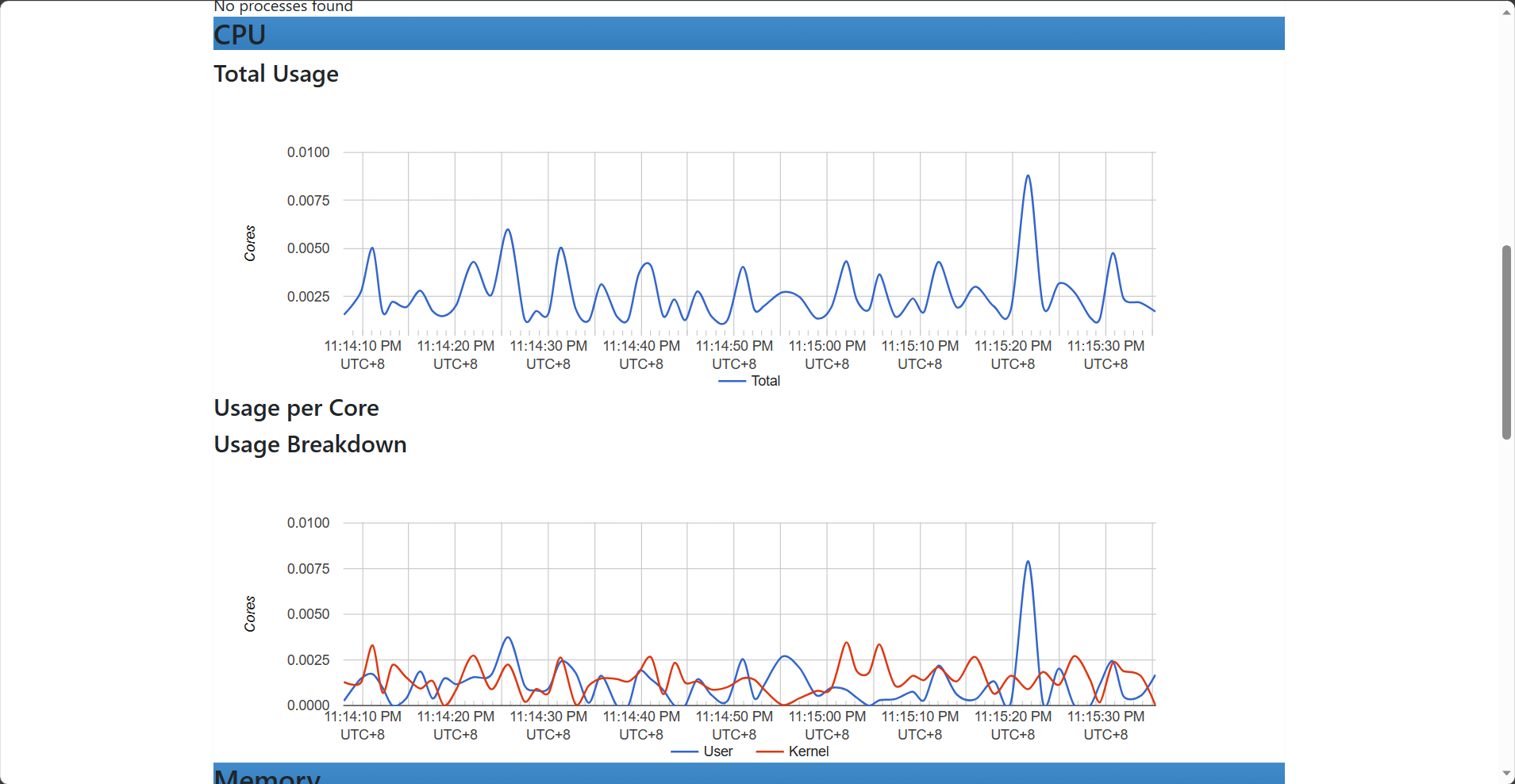
腾讯mini项目-【指标监控服务重构】2023-08-26
今日已办 Venus 的 Trace 无感化 定义 handler 函数 fiber.Handler 的主要处理逻辑返回处理中出现的 error返回处理中响应 json 的函数 // handler // Description: // Author xzx 2023-08-26 18:00:03 // Param c // Return error // Return func() error : function for …...
)
《Essential C++》之(面向过程泛型编程)
目录 🌼面向过程的编程风格 -- 第2章 🍈2.2 🍈2.4 🍈2.5 🍈2.6 🌼泛型编程风格 -- 第3章 🍍3.1 🍍3.4 前言 要求 完整代码 输入输出 🌼面向过程的编程风…...

机器学习笔记:adaBoost
1 介绍 AdaBoost(Adaptive Boosting)是一种集成学习方法,它的目标是将多个弱分类器组合成一个强分类器 通过反复修改训练数据的权重,使得之前分类错误的样本在后续的分类器中得到更多的关注每一轮中,都会增加一个新的…...
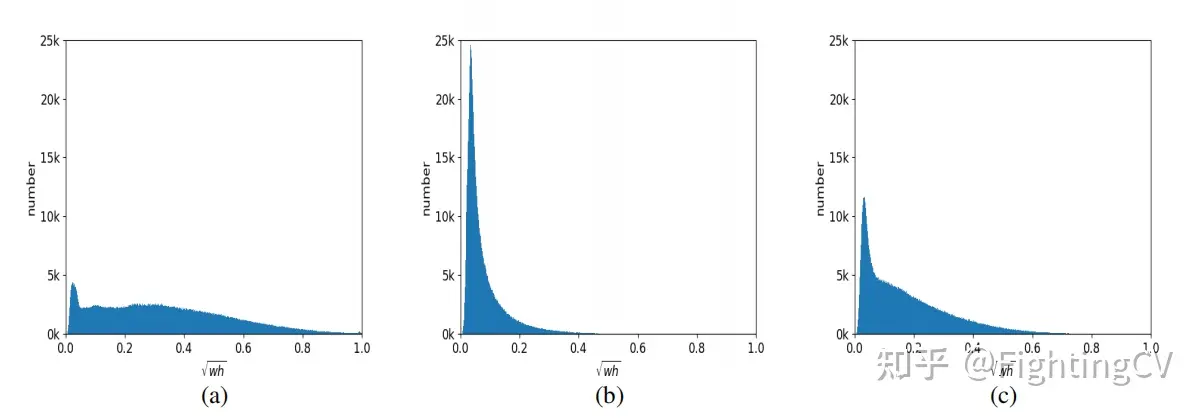
Anchor DETR
Anchor DETR(AAAI 2022) 改进: 提出了基于anchor的对象查询提出Attention变体-RCDA 在以前DETR中,目标的查询是一组可学习的embedding。然而,每个可学习的embedding都没有明确的意义 (因为是随机初始化的)ÿ…...

适合在家做的副业 整理5个,有电脑就行
今天,我们不说别的,整理5个适合个人在家单干的副业。需要电脑,如果你没电脑就不用看了,最后两个,我们也在做,你可以看到最后了解。这些副业,大家多去实践操作,前期,每月三…...

Android WebSocket
WS Android WebSocket 资源 名字资源AAR下载GitHub查看Gitee查看 Maven 1.build.grade allprojects {repositories {...maven { url https://jitpack.io }} }2./app/build.grade dependencies {implementation com.github.RelinRan:WS:2022.2023.9.23.1 }初始化 配置权…...

Android 按键流程
一、驱动层流程 主要流程涉及以下文件 kernel/msm-4.19/drivers/input/keyboard/gpio_keys.c kernel/msm-4.19/drivers/input/input.c kernel/msm-4.19/drivers/input/evdev.c kernel/msm-4.19/drivers/input/input-compat.c 有按键动作时,根据 dtsi 中配置 c…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
