Python经典练习题(四)
文章目录
- 🍀第一题
- 🍀第二题
- 🍀第三题
🍀第一题
题目:打印出如下图案(菱形):

我们首先分析一下,本题实现的步骤主要有两个,分别是前四行和后三行
- 前四行:第一行三空格+一*,第二行两空格+三*,第三行一空格+五*,第四行五空格+七*
- 后三行:第一行一空格五*,第二行两空格+三*,第三行三空格+一*
这里我们就可以找到规律了,如果以行为函数的参数,我们不妨将其设定为外循环的参数
代码如下
def f1(rowup): # 前四行for i in range(rowup):for j in range(rowup - i):print(' ',end='')for k in range(2 * i +1):print("*",end='')print()def f2(rowdown): # 后三行for i in range(rowdown):for j in range(i + 2):print(" ",end='')for k in range(5- 2 * i):print("*",end='')print()
运行结果

🍀第二题
有一分数序列:2/1,3/2,5/3,8/5, 13/8,21/13…求出这个数列的前20项之和。
def generate_fibonacci(n):fib = [0, 1] # 初始化斐波那契数列的前两项while len(fib) < n:next_fib = fib[-1] + fib[-2] # 计算下一项fib.append(next_fib) # 将下一项添加到列表中return fib# 生成斐波那契数列的前n项
n = 23 # 你可以替换成任何你想要的项数
fibonacci_sequence = generate_fibonacci(n)
sum_numbers= []for i in range(20):result = float(fibonacci_sequence[3:][i] / fibonacci_sequence[2:][i])sum_numbers.append(result)
print(sum(sum_numbers))
本题我的思路采用列表切片,看起来有点傻,但是能做出来就是好滴
运行结果如下

🍀第三题
题目:求1+2!+3!+…+20!的和。
本题采用三种方法进行求解
方法一:使用循环计算阶乘和求和
def factorial(n):result = 1for i in range(1, n + 1):result *= ireturn resultn = 20
total = sum(factorial(i) for i in range(1, n + 1))
print("方法一的结果:", total)
方法一:使用循环计算阶乘和求和
这个方法使用了一个for循环来计算每个数字的阶乘,然后将它们相加以得到最终的和。具体思路如下:
- 创建一个函数factorial(n),它接受一个整数n作为输入,并返回n的阶乘。
- 在主程序中,通过一个for循环遍历从1到20的所有数字,分别调用factorial()函数来计算它们的阶乘。
- 将每个阶乘值加到一个累加器变量中,最终得到总和。
方法二:使用递归计算阶乘和求和
def factorial(n):if n == 0:return 1else:return n * factorial(n - 1)n = 20
total = sum(factorial(i) for i in range(1, n + 1))
print("方法二的结果:", total)
方法二:使用递归计算阶乘和求和
这个方法使用了递归来计算每个数字的阶乘,然后将它们相加以得到最终的和。具体思路如下:
- 创建一个函数factorial(n),它接受一个整数n作为输入,并返回n的阶乘。
- 在factorial()函数内部,使用递归来计算阶乘。基本情况是当n为0时,阶乘为1;否则,递归调用factorial(n-1)并将结果与n相乘。
- 在主程序中,通过一个for循环遍历从1到20的所有数字,分别调用factorial()函数来计算它们的阶乘。
- 将每个阶乘值加到一个累加器变量中,最终得到总和。
方法三:使用预先计算好的阶乘值求和
def precompute_factorials(n):factorials = [1]for i in range(1, n + 1):factorials.append(factorials[-1] * i)return factorialsn = 20
factorials = precompute_factorials(n)
total = sum(factorials[i] for i in range(1, n + 1))
print("方法三的结果:", total)
方法三:使用预先计算好的阶乘值求和
这个方法首先预先计算了1到20的所有数字的阶乘值,然后直接使用这些值来求和。具体思路如下:
- 创建一个函数precompute_factorials(n),它接受一个整数n作为输入,并返回一个包含1到n的所有数字的阶乘值的列表。
- 在precompute_factorials()函数内部,使用一个for循环来计算1到n的所有数字的阶乘,并将它们存储在列表中。
- 在主程序中,调用precompute_factorials(20)来获取1到20的所有数字的阶乘值列表。
- 使用一个for循环遍历从1到20的所有数字,直接从阶乘值列表中取出对应的阶乘值,并将它们相加以得到总和。

挑战与创造都是很痛苦的,但是很充实。
相关文章:

Python经典练习题(四)
文章目录 🍀第一题🍀第二题🍀第三题 🍀第一题 题目:打印出如下图案(菱形): 我们首先分析一下,本题实现的步骤主要有两个,分别是前四行和后三行 前四行:第一…...

Mac Pro在重装系统时提示“未能与恢复服务器取得联系”
检查网络连接: 确保你的Mac Pro连接到稳定的网络。尝试更换其他网络,例如切换到不同的Wi-Fi或使用有线连接。 系统时间校正: 错误的系统时间有时会导致与恢复服务器的连接问题。在恢复模式下打开终端(在实用工具菜单中选择终端&a…...

【C/C++】指针常量、常量指针、指向常量的常指针
目录 1.概念2. const pointer3. pointer to a constant3.1 (pointer to a constant)-constant3.2 poiner-constant3.3 (pointer to a constant)-variable3.4 poiner-variable3.5 多层级关系时的兼容3.6 用处 4. a constant pointer to a constant 1.概念 首先明确这几个术语的…...
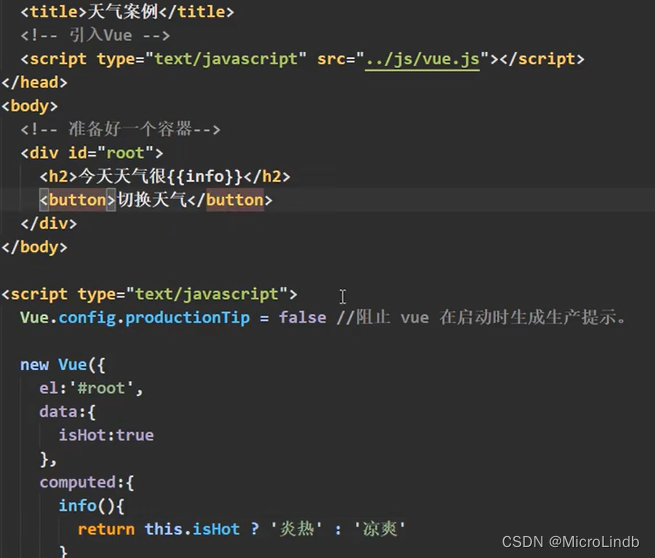
【VUE复习·4】计算属性computed:原理、完整写法(不常用)、与 methods 的区别、简写(最常用)、应用案例!
总览 1.简介计算属性 2.computed 与 methods 的区别 3.computed 的简写(不修改计算属性,只显示) 4.经典应用场景 一、计算属性 1.为什么需要计算属性? 首先,如果我们要写一个插值语法,而 {{ }} 内的内容…...

Linux 基本语句_编译C过程
Linux撰写C语言并编译的过程 1、预处理 将所有的#define删除,并且展开所有的宏定义,并且处理所有的条件预编译指令,比如#if #ifdef #elif #else #endif等。处理#include预编译指令,将被包含的文件插入到该预编译指令的位置。删除…...

MYSQL8解压版 windows 主从部署步骤及配置(包含配置文件,教程文件,免积分下载)
MYSQL8解压版 windows 主从部署步骤及配置 一.安装MSYQL 这里只讲大概,详细步骤、my.ini文件、安装包等会在页尾文件中(正常情况按首个mysql安装,只是名字有区别) 1.主库my.ini配置 [mysqld] #典型的值是5-6GB(8GB内存),8-11GB(16GB内存), 20-25GB(32GB内存)&…...

RabbitMQ的基本介绍
什么是MQ 本质是一个队列,只不过队列中存放的信息是message罢了,还是一种跨进程的通信机制,用于上下游传递信息。在互联网架构中,MQ是一种非常常见的上下游“逻辑解耦物理解耦”的消息通信服务。使用了MQ之后,信息发送…...
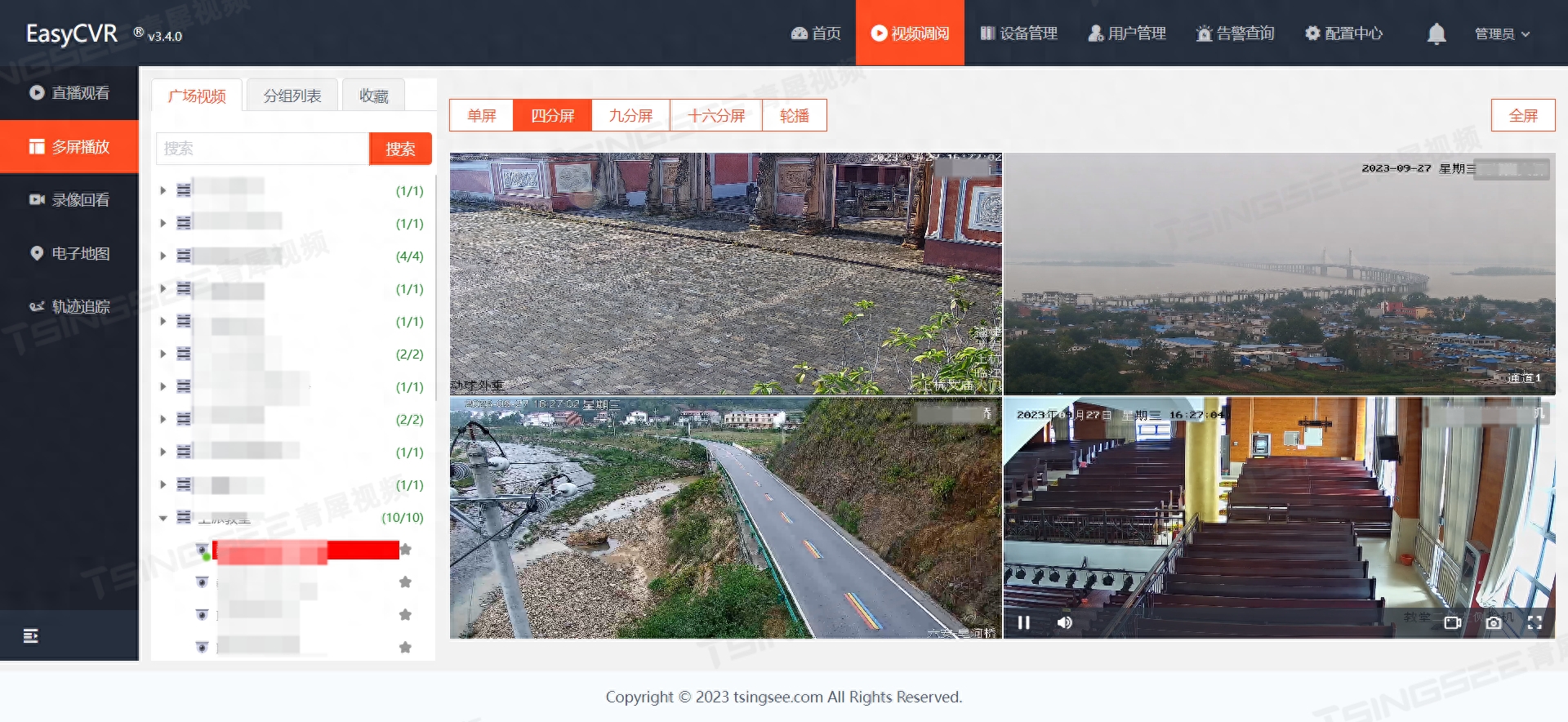
AI智能视频监控技术如何助力美好乡村建设?
随着城市化发展,很多乡村设施也在逐渐完善,智能监控也成了乡村发展必不可少的一环,智能视频监控应该在乡村建设里如何发挥作用呢? 1、有效提升安全意识 通过在乡村重要区域、公共场所、道路等设置智能视频监控设备,可…...

【网络安全】2023年堡垒机品牌大全
随着大家网络安全意识的增加,随着国家等保政策的严格执行,越来越多的企业开始采购堡垒机。这里就给大家总结了部分堡垒机品牌,让大家参考参考。 2023年堡垒机品牌大全 1、行云堡垒 2、JumpServer 3、安恒 4、骞云 5、齐治 6、阿里云 …...
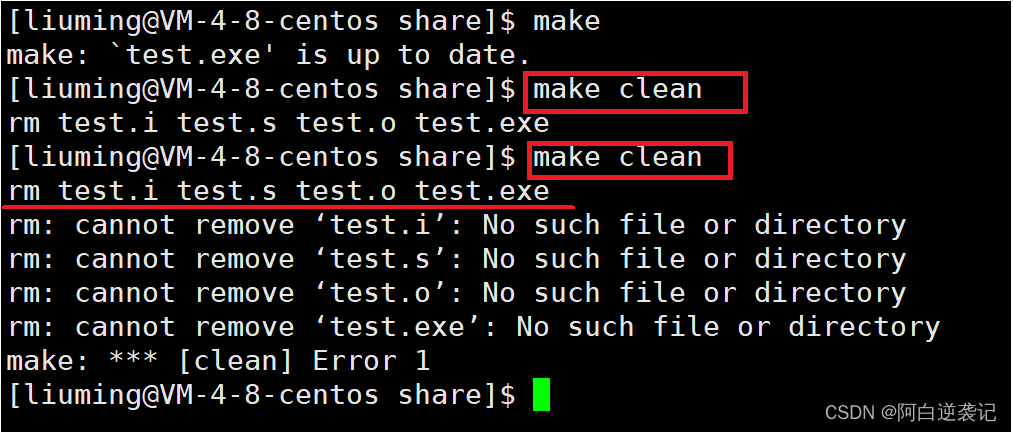
makefile相关知识的讲解
目录 makefile文件的介绍 step1:手动创建一个makefile文件 step2:在文件当中编辑指定的命令 step3:退出makefile文件并使用make执行文件当中的命令 step4:使用clean指令清除生成的文件 makefile当中的命令编写方式 目标文件和依…...
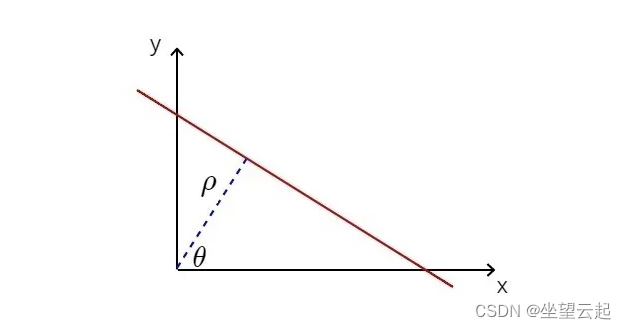
OpenCV中的HoughLines函数和HoughLinesP函数到底有什么区别?
一、简述 基于OpenCV进行直线检测可以使用HoughLines和HoughLinesP函数完成的。这两个函数之间的唯一区别在于,第一个函数使用标准霍夫变换,第二个函数使用概率霍夫变换(因此名称为 P)。概率版本之所以如此,是因为它仅分析点的子集并估计这些点都属于同一条线的概率。此实…...
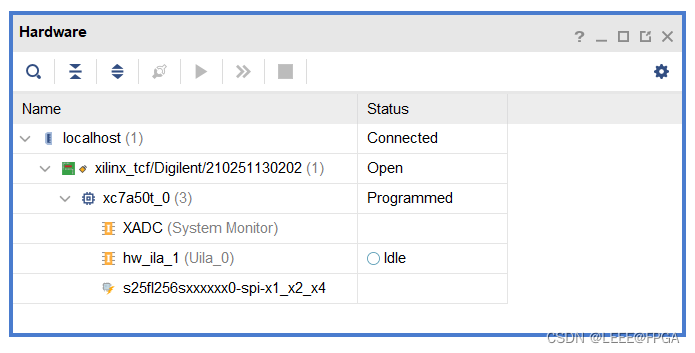
Xilinx FPGA 程序固化重新上电程序不运行的问题
问题描述 FPGA直接下载bit文件,功能正常。 FPGA擦除FLASH,烧写FLASH,正常。 电源断电,重新上电,FALSH里面的程序没有启动,FPGA程序没有跑起来。–FLASH启动不正常。 解决办法 在XDC约束文件里边增加约束: ## Configuration options, can be used for all designs se…...
c++ 使用rapidjson对数据序列化和反序列化(vs2109)
RapidJSON是腾讯开源的一个高效的C JSON解析器及生成器,它是只有头文件的C库,综合性能是最好的。 1. 安装 在NuGet中为项目安装tencent.rapidjson 2. 引用头文件 #include <rapidjson/document.h> #include <rapidjson/memorystream.h> #…...

4.迭代最近点ICP及非线性优化求解
使用非线性优化方法求解ICP 文章目录 使用非线性优化方法求解ICP前情提要ICP问题回顾对矩阵变量求导数 ICP问题的非线性解法代码示例 欢迎访问个人网络日志🌹🌹知行空间🌹🌹 前情提要 在迭代最近点算法ICP及SVD求解中介绍了ICP问…...
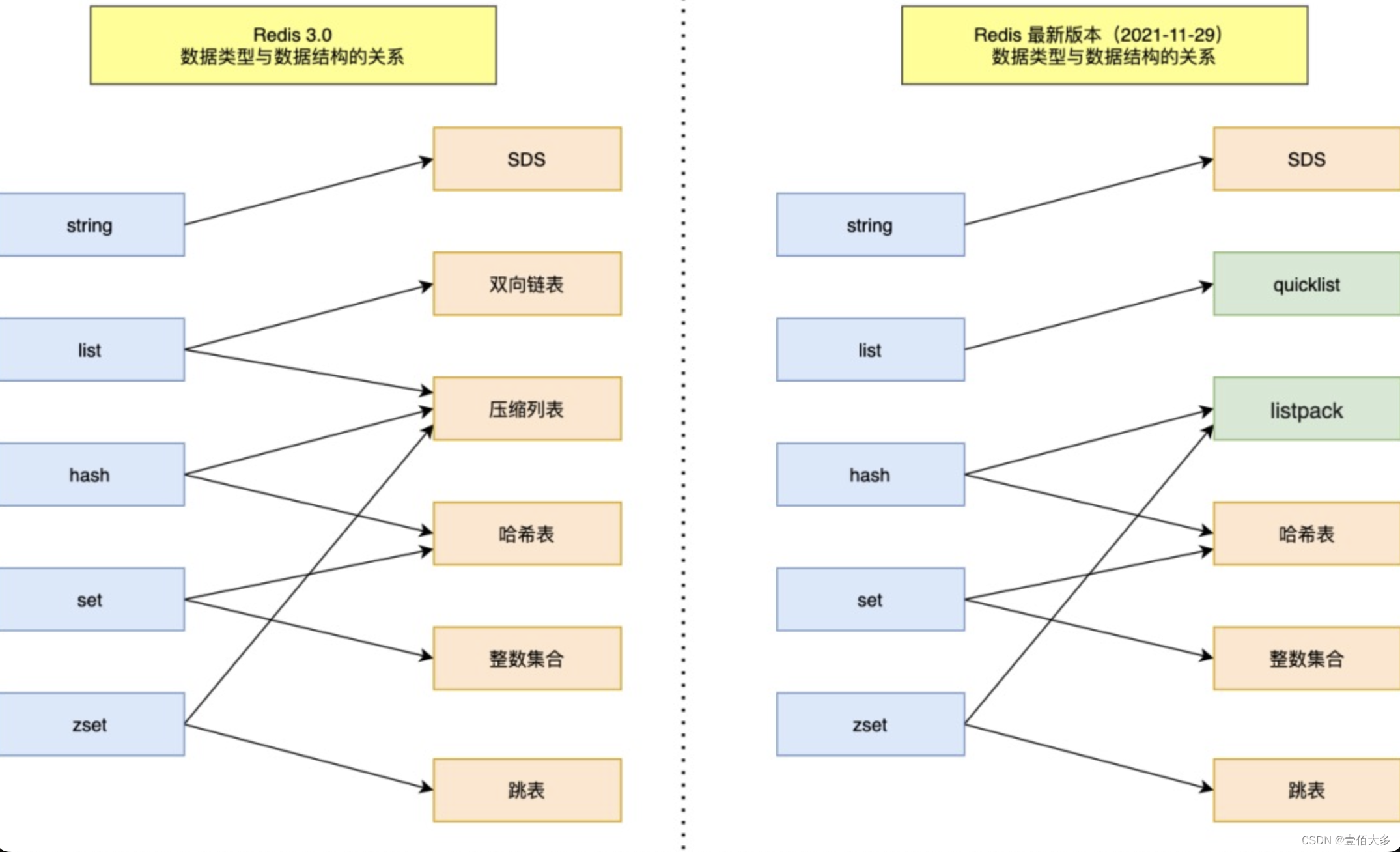
【redis总结】
文章目录 1、redis简介2、为什么要选择redis做缓存3、数据结构4、redis多线程模型redis6.0的变化 5、redis持久化AOF的实现过程RDB的实现过程 6、redis集群的搭建7、 redis过期删除和淘汰策略8、redis的内存淘汰策略 1、redis简介 Redis(Remote Dictionary Server&…...

图数据库:释放关系的力量
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 在数据管理领域,图数据库已经成为一种强大的工具,它彻底改变了我们处理和分析复杂关系的方式。与依赖表和列的传统关系数据库不同,图…...

Windows系统如何临时关闭“Windows安全中心实时保护”
前言 启动windows depender实时保护可能会使系统不太流畅,也可能会导致我们的程序无法正常运行,因为它会拦截或搜索我们的正常工作。 暂时关闭windows depender的实时保护对许多用户来说非常重要。 一、Win10系统关闭方法 打开Windows安全中心&#…...
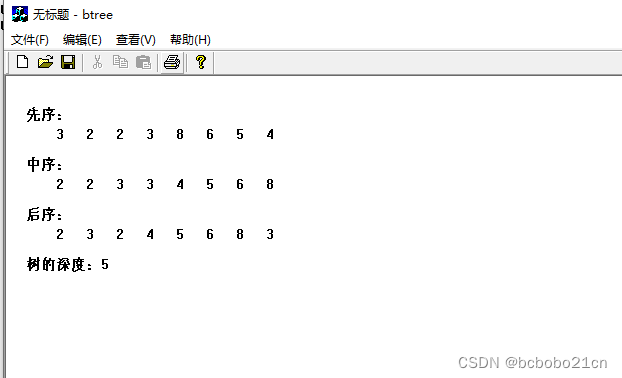
二叉树MFC实现
设有一颗二叉树如下; 这似乎是一颗经常用作示例的二叉树; 对树进行遍历的结果是, 先序为:3、2、2、3、8、6、5、4, 中序为:2、2、3、3、4、5、6、8, 后序为2、3、2、4、5、6、8、3;…...

Nginx之客户并发数限制解读
目录 基本介绍 配置指令 limit_conn_zone limit_conn 其他 limit_rate limit_rate_after limit_req_zone limit_req 基本介绍 在我们进行系统开发设计中,要考虑服务器流量异常,负载过大等问题。对于大流量恶意的攻击访问,会带来带宽…...
白捡一个存储型XSS
本文由掌控安全学院 - 杳若 投稿 起因 利用fofa搜索时发现 org"China Education and Research Network Center" && body"/register" 任意用户注册 在找到该CMS的时候发现存在任意用户注册的情况 http://xxxx.edu.cn/student/Register.ashx …...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
