【学习笔记】[ARC153F] Tri-Colored Paths
假设三种颜色的边都存在,并且不存在这样的路径
首先观察到,对于一个简单环上的边,颜色一定相同
因此,考虑建立圆方树,问题转化为圆方树上的 D P DP DP问题。限制是对于方点所连接的边,必须涂上相同的颜色,也就是不存在一条路径上有三种颜色的方点
注意到,如果有两个相邻的颜色不同的方点,那么其对应的子树内的方点一定只有一种颜色。又因为三种颜色的方点都出现过,因此将圆点删除后,剩下的连通块内方点也一定只有一种颜色。考虑到圆方树的性质:只有方点和圆点有边相连,因此枚举这个圆点并统计答案即可。
需要注意的是,当 n ≤ 4 n\le 4 n≤4时需要暴搜解决。这是因为环上会出现反例。同理,对于大小为 3 3 3的点双也要特判(环上的点颜色互不相同,出边只有一条,其他边的颜色都和环上某一条边的颜色相同)。
复杂度 O ( n + m ) O(n+m) O(n+m)。
remark \text{remark} remark 对于圆方树上的 D P DP DP问题,分析性质有时候比设计状态更重要。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define fi first
#define se second
#define db double
#define ull unsigned long long
#define inf 0x3f3f3f3f
using namespace std;
const int mod=998244353;
const int N=2e5+5;
int n,m,cnt;
int dfn[N],low[N],du[N],num;
vector<int>G[N];
stack<int>s;
ll res;
ll fpow(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
vector<int>vec[N];
void tarjan(int u){dfn[u]=low[u]=++num,s.push(u);for(auto v:G[u]){if(!dfn[v]){tarjan(v),low[u]=min(low[u],low[v]);if(low[v]>=dfn[u]){int tmp=0;du[u]++,cnt++;do{tmp=s.top(),s.pop();du[tmp]++,vec[cnt].pb(tmp);}while(tmp!=v);vec[cnt].pb(u);}}else low[u]=min(low[u],dfn[v]);}
}
void add(ll &x,ll y){x=(x+y)%mod;
}
vector<pair<int,int>>edge;
int w[10][10],p[10];
void dfs(int x){if(x==m){int ok=0;for(int i=1;i<=n;i++)p[i]=i;do{int sz=0;for(int i=2;i<=n;i++){if(~w[p[i]][p[i-1]]){sz|=1<<w[p[i]][p[i-1]]-1;if(sz==7)break;}else break;}if(sz==7){ok=1;break;}}while(next_permutation(p+1,p+1+n));res+=ok;return;}int u=edge[x].fi,v=edge[x].se;for(int i=1;i<=3;i++){w[u][v]=w[v][u]=i,dfs(x+1);}
}
signed main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m;for(int i=1;i<=m;i++){int x,y;cin>>x>>y;G[x].pb(y),G[y].pb(x),edge.pb({x,y});}if(n<=3){cout<<0;return 0;}if(n==4){memset(w,-1,sizeof w),dfs(0);cout<<res;return 0;}for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);res=(fpow(3,m)-3*fpow(2,m)+3)%mod;for(int i=1;i<=n;i++){if(du[i]>=3){add(res,-fpow(3,du[i])+3*fpow(2,du[i])-3);}}for(int i=1;i<=cnt;i++){if(vec[i].size()==3){int tot=0;for(auto e:vec[i])if(du[e]>1)tot++;if(tot<=1)add(res,-6);}}cout<<(res+mod)%mod;
}
相关文章:

【学习笔记】[ARC153F] Tri-Colored Paths
假设三种颜色的边都存在,并且不存在这样的路径 首先观察到,对于一个简单环上的边,颜色一定相同 因此,考虑建立圆方树,问题转化为圆方树上的 D P DP DP问题。限制是对于方点所连接的边,必须涂上相同的颜色…...
基于SSM的实习管理系统
基于SSM的实习管理系统、前后端分离 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 管理员界面 教师 学生 研究背景 基于SSM的实习管理系统是一个基于Spring、Spring…...
在Vue中通过ElementUI构建前端页面【登录,注册】,在IEDA构建后端实现前后端分离
一.ElementUI组件入门 1.对于ElementUI的理解 是一套基于 Vue.js 的开源UI组件库,提供了丰富的可复用组件,可以帮助开发者快速构建美观、易用的前端界面 2.Element UI 的特点和优势 多样化的组件:Element UI 提供了众多常用的基础组件&#…...

TX2 open ttyTHS2
TX2 open ttyTHS2 #冷风那个吹# 于 2019-04-01 14:10:43 发布 1749 收藏 6 分类专栏: 平时问题积累 TX2 版权 平时问题积累 同时被 2 个专栏收录 22 篇文章0 订阅 订阅专栏 TX2 30 篇文章8 订阅 订阅专栏 TX2上有5个串口,但是ttyTHS1是调试串口,ttyTHS3是蓝牙,ttyTHS…...

conan入门(二十八):解决conan 1.60.0下 arch64-linux-gnu交叉编译openssl/3.1.2报错问题
上一篇博客《conan入门(二十七):因profile [env]字段废弃导致的boost/1.81.0 在aarch64-linux-gnu下交叉编译失败》解决了conan 1.60.0交叉编译boost/1.80.1的问题后,我继续交叉编译openssl/3.1.2时又报错了 conan install openssl/3.1.2 -pr:h aarch64-linux-gnu.…...

Xcode 15 运行<iOS 14, 启动崩溃问题
如题. Xcode 15 启动 < iOS 14(没具体验证过, 我的问题设备是iOS 13.7)真机设备 出现启动崩溃 解决方案: Build Settings -> Other Linker Flags -> Add -> -ld64...
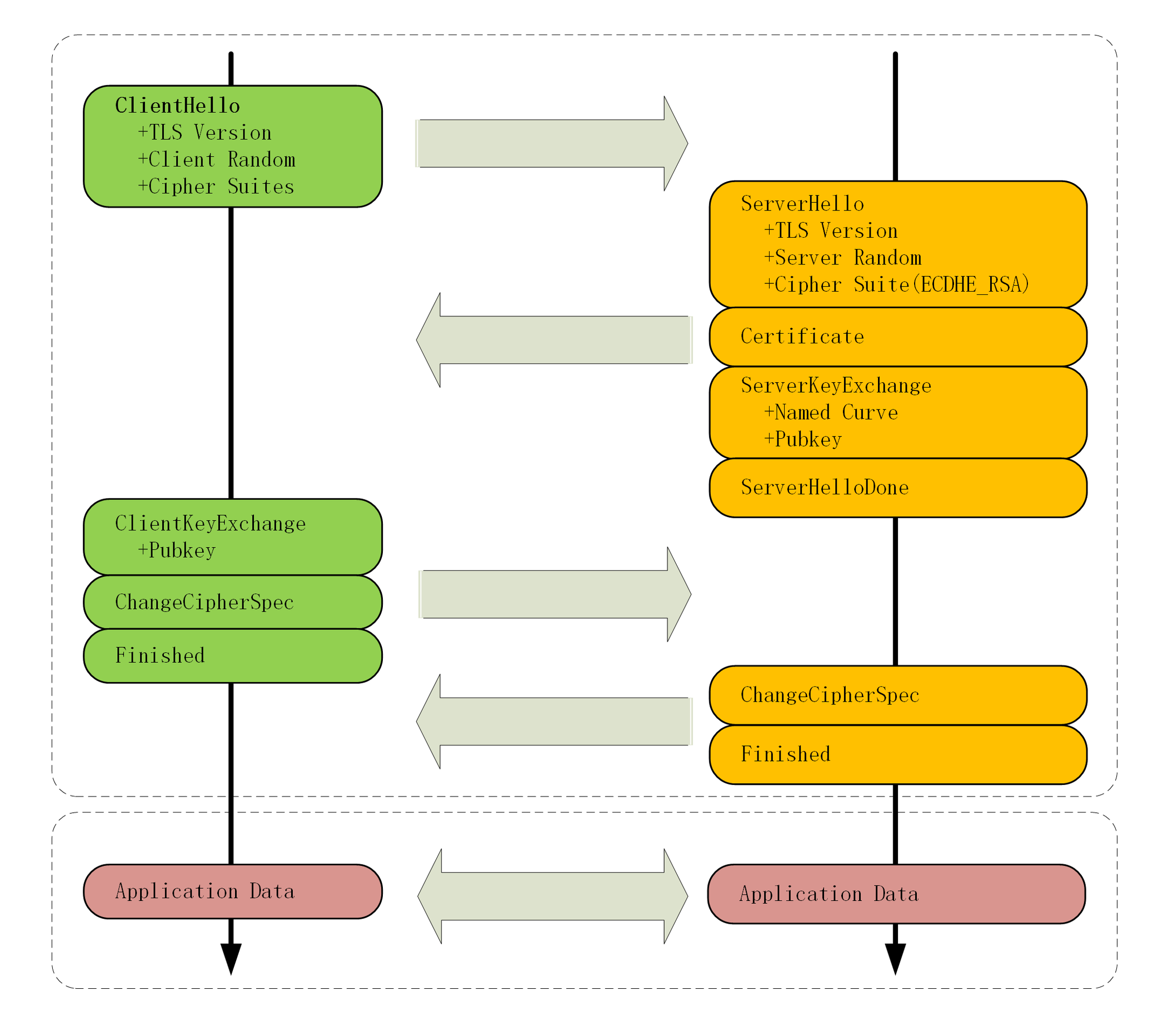
HTTPS协议概述
HTTPS(Hypertext Transfer Protocol over Secure Socket Layer,基于安全套接字层的超文本传输协议),是以安全为目标的HTTP通道,简单讲是HTTP的安全版。即HTTP下加入SSL层,HTTPS的安全基础是SSL,…...
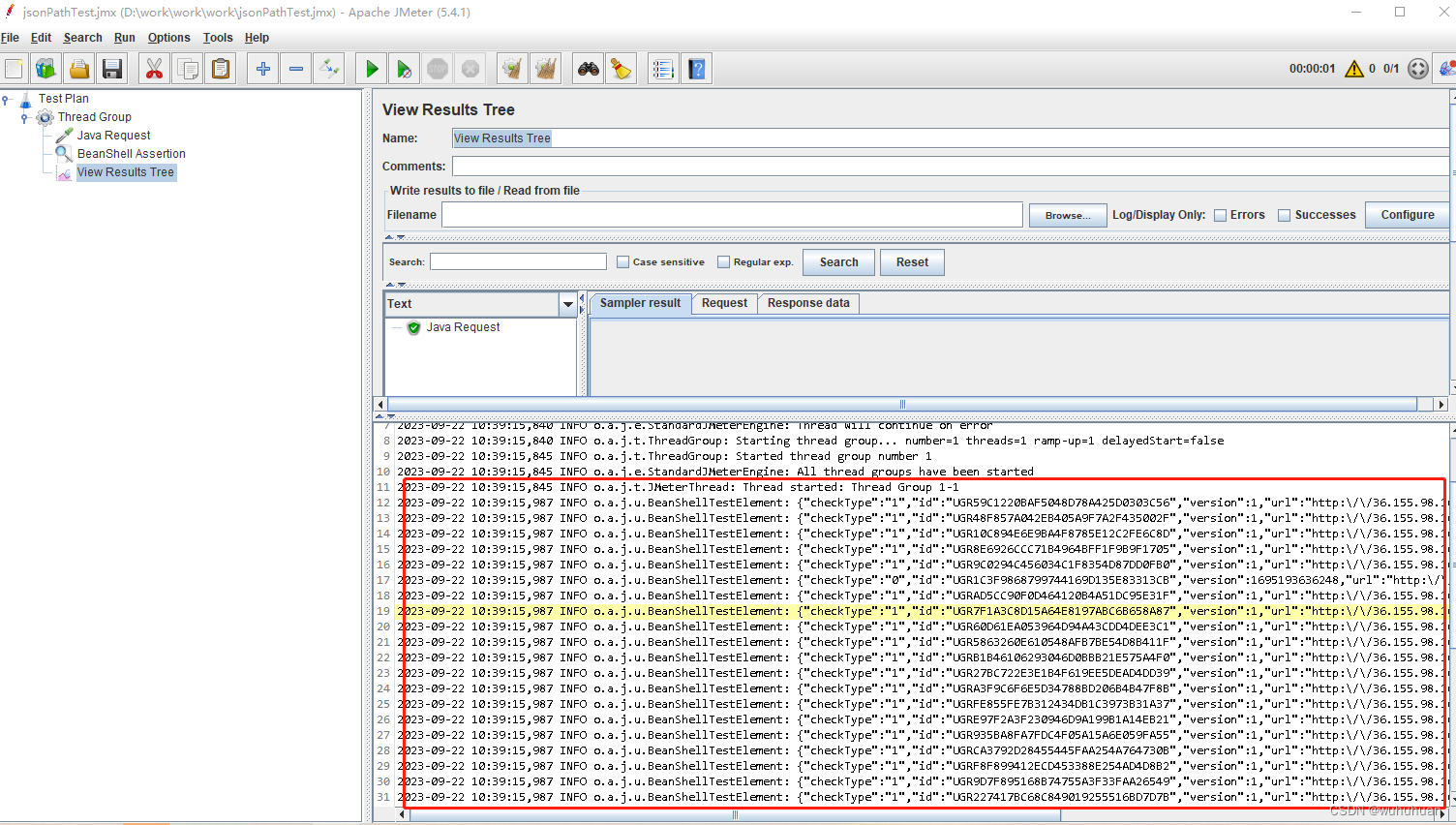
jmeterbeanshell调用jsonpath获取对应值
1.jmeter 新建线程组、Java Request、BeanShell Assertion、View Results Tree 2、在BeanShell Assertion中贴入代码: import org.apache.jmeter.extractor.json.jsonpath.JSONManager; import java.util.List; JSONManager js new JSONManager(); String jsonStr…...

C++中实现雪花算法来在秒级以及毫秒及时间内生成唯一id
1、雪花算法原理 雪花算法(Snowflake Algorithm)是一种用于生成唯一ID的算法,通常用于分布式系统中,以确保生成的ID在整个分布式系统中具有唯一性。它的名称来源于雪花的形状,因为生成的ID通常是64位的整数࿰…...
)
OPTEE Gprof(GNU profile)
安全之安全(security)博客目录导读 OPTEE调试技术汇总 目录 一、序言 二、Gprof使用 三、Gprof实现 1、Call graph information 2、PC distribution over time 一、序言 本文描述了如何使用gprof对TA进行概要分析。 配置选项CFG_TA_GPROF_SUPPORTy使OP-TEE能够从在用户模…...

MySQL 事务的操作指南(事务篇 二)
基本操作 事务的提交方式:自动提交(autocommit1)和手动提交(autocommit0) 查询和修改事务提交方式: -- 查看事务提交方式(标识表示这是个系统变量) select autocommit ;-- 修改事务提交方式为自动提交 …...

Oracle 查询 SQL 语句
目录 1. Oracle 查询 SQL 语句1.1. 性能查询常用 SQL1.1.1. 查询最慢的 SQL1.1.2. 列出使用频率最高的 5 个查询1.1.3. 消耗磁盘读取最多的 sql top51.1.4. 找出需要大量缓冲读取(逻辑读)操作的查询1.1.5. 查询每天执行慢的 SQL1.1.6. 从 V$SQLAREA 中查询最占用资源的查询1.1.…...

gin 基本使用
gin 初体验 import ("net/http""github.com/gin-gonic/gin" )func main() {r : gin.Default()r.GET("/ping", func(c *gin.Context) {c.JSON(http.StatusOK, gin.H{"message": "pong",})})r.Run() }gin 路由接受一个 type …...
8月最新修正版风车IM即时聊天通讯源码+搭建教程
8月最新修正版风车IM即时聊天通讯源码搭建教程。风车 IM没啥好说的很多人在找,IM的天花板了,知道的在找的都知道它的价值,开版好像就要29999,后端加密已解,可自己再加密,可反编译出后端项目源码,已增加启动后端需要google auth双重验证,pc端 web端 wap端 android端 ios端 都有 …...

NSDT孪生场景编辑器系统介绍
一、产品背景 数字孪生的建设流程涉及建模、美术、程序、仿真等多种人才的协同作业,人力要求高,实施成本高,建设周期长。如何让小型团队甚至一个人就可以完成数字孪生的开发,是数字孪生工具链要解决的重要问题。考虑到数字孪生复杂…...
3D WEB轻量化引擎HOOPS助力3D测量应用蓬勃发展:效率、精度显著提升
在3D开发工具领域,Tech Soft 3D打造的HOOPS SDK已经崭露头角,成为了全球领先的3D领域开发工具提供商。HOOPS SDK包括四种不同的3D软件开发工具,已成为行业的翘楚。 其中,HOOPS Exchange以其CAD数据转换的能力脱颖而出,…...

【Orange Pi】Orange Pi5 Plus 安装记录
官网:Orange Pi - Orangepi 主控芯片:Rockchip RK3588(8nm LP制程)NPU:内嵌的 NPU 支持INT4/INT8/INT16/FP16混合运算,算力高达 6Top支持的操作系统: Orangepi OS(Droid)Orangepi O…...

NLP 项目:维基百科文章爬虫和分类 - 语料库阅读器
塞巴斯蒂安 一、说明 自然语言处理是机器学习和人工智能的一个迷人领域。这篇博客文章启动了一个具体的 NLP 项目,涉及使用维基百科文章进行聚类、分类和知识提取。灵感和一般方法源自《Applied Text Analysis with Python》一书。 在接下来的文章中,我将…...
查看吾托帮88.47的docker里的tomcat日志
步骤如下 (1)ssh (2)ssh root192.168.88.47 等待输入密码:fytest (3)pwd #注释:输出/root (4)docker exec -it wetoband_deploy /bin/bash #注释࿱…...

衷心 祝愿
达之云衷心祝愿您,中秋国庆双节快乐,阖家幸福!感谢您们一直以来对达之云的关注与支持。 双节来临之际,达之云发布全新产品——达之云CDP客户数据平台(Dazdata CDP),致力于为中小企业提供互联网营…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
