机器人中的数值优化|【六】线性共轭梯度法,牛顿共轭梯度法
机器人中的数值优化|【六】线性共轭梯度法,牛顿共轭梯度法
往期回顾
机器人中的数值优化|【一】数值优化基础
机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例
机器人中的数值优化|【三】无约束优化,拟牛顿法理论与推导
机器人中的数值优化|【四】L-BFGS理论推导与延伸
机器人中的数值优化|【五】BFGS算法非凸/非光滑处理
关于牛顿-共轭梯度法,笔者认为对其最直接和最根本的认识,这篇帖子写得特别好,可以参考東雲正樹的 如何理解共轭梯度法 一文。
为什么要用Conjugate Gradient method?
从前面的系列我们知道,对于一个凸的无约束优化,我们总是希望通过梯度,基于这样那样的方法来到达最优点。在前面基本的梯度下降方法中,我们每次计算一个梯度,并根据线性搜索得到的一个较为不错的步长,向前优化一步。在Newton-CG method中我们不禁要提问了:有没有一种可以有确定的搜索次数,而且次数还比较少的方法呢?这个方法就是Newton-CG method。我们知道在向量中存在标准正交集的概念,在优化问题中,我们也存在共轭梯度的概念,关于共轭梯度的具体定义和推导可以进一步查阅相关的资料。本质上,就是把原来随机走梯度的过程,变为在凸问题空间中“正交”的梯度向量上,每个向量只走一步,且是最优的一步的过程。
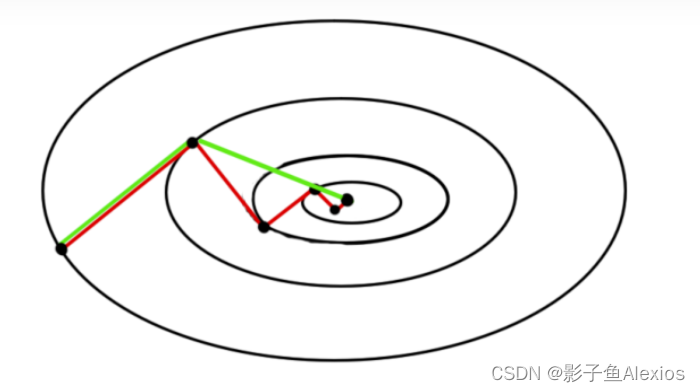
从上面的例子我们可以看到,绿色为共轭梯度法,红色为梯度下降法,我们其实要做的工作就是在椭圆的切向和法向各走“最优”的一步,一步到位即可。
Gram-Schmitd正交化/施密特正交化
理解共轭梯度法,首先我们要回顾一个东西,那就是施密特正交化。利用施密特正交化,我们可以从空间中的一组向量得到互相正交的一组向量集。如果我们有一组互不平行的向量 [ α 1 , α 2 , α 3 , α 4 , α 5 , . . . ] {[\alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5,...]} [α1,α2,α3,α4,α5,...],利用一下公式可以得到正交基:
β 1 = α 1 \beta_1 = \alpha_1 β1=α1
β 2 = α 2 − ( β 1 , α 2 ) ( β 1 , β 1 ) β 1 \beta_2 = \alpha_2 - \frac{(\beta_1, \alpha_2)}{(\beta_1, \beta_1)} \beta_1 β2=α2−(β1,β1)(β1,α2)β1
β 3 = α 3 − ( β 1 , α 3 ) ( β 1 , β 1 ) β 1 − ( β 2 , α 3 ) ( β 2 , β 2 ) β 2 \beta_3 = \alpha_3 - \frac{(\beta_1, \alpha_3)}{(\beta_1, \beta_1)} \beta_1 - \frac{(\beta_2, \alpha_3)}{(\beta_2, \beta_2)} \beta_2 β3=α3−(β1,β1)(β1,α3)β1−(β2,β2)(β2,α3)β2
β 4 = α 4 − ( β 1 , α 4 ) ( β 1 , β 1 ) β 1 − ( β 2 , α 4 ) ( β 2 , β 2 ) β 2 − ( β 3 , α 4 ) ( β 3 , β 3 ) β 3 \beta_4 = \alpha_4 - \frac{(\beta_1, \alpha_4)}{(\beta_1, \beta_1)} \beta_1 - \frac{(\beta_2, \alpha_4)}{(\beta_2, \beta_2)} \beta_2 - \frac{(\beta_3, \alpha_4)}{(\beta_3, \beta_3)} \beta_3 β4=α4−(β1,β1)(β1,α4)β1−(β2,β2)(β2,α4)β2−(β3,β3)(β3,α4)β3
. . . ... ...
线性共轭梯度法
对于如下的一个问题
a r g m i n x f ( x ) = 1 2 x T A x − b T x argmin_x f(x) = \frac{1}{2}x^TAx - b^Tx argminxf(x)=21xTAx−bTx
我们要求其无约束优化。这里我们可以引入共轭梯度的概念,其概念类似于正交向量,对于一个正交向量 u , v u,v u,v,有 u T v = 0 u^Tv =0 uTv=0。一个矩阵 A A A,如果存在向量 u , v u,v u,v,有 u T A v = 0 u^TAv=0 uTAv=0,则我们认为 u , v u,v u,v关于 A A A共轭。在下降过程中,如果我们每一步选择的下降方向都是一个独立的共轭向量,且一共有 n n n个共轭向量,则最多需要 n n n步即可下降到最优点。
回顾优化过程,最核心的公式为
x k + 1 = x k + α u k x_{k+1} = x_k + \alpha u_k xk+1=xk+αuk
其中 u k u_k uk为下降方向, α \alpha α为步长。将 x k + 1 x_{k+1} xk+1代入最优化目标公式,我们有
a r g m i n x f ( x k + 1 ) = a r g m i n x f ( x k + α u k ) argmin_x f(x_{k+1}) = argmin_x f(x_k + \alpha u_k) argminxf(xk+1)=argminxf(xk+αuk)
假设下降方向已经确定了,我们要确定最优步长
a r g m i n x f ( x k + α u k ) = a r g m i n x 1 2 ( x k + α u k ) T A ( x k + α u k ) − b T ( x k + α u k ) argmin_x f(x_k + \alpha u_k) = argmin_x \frac{1}{2}(x_k + \alpha u_k)^TA(x_k + \alpha u_k) - b^T(x_k + \alpha u_k) argminxf(xk+αuk)=argminx21(xk+αuk)TA(xk+αuk)−bT(xk+αuk)
对 α \alpha α求导,有
a r g m i n x f ′ ( x k + α u k ) = 0 argmin_x f'(x_k + \alpha u_k) = 0 argminxf′(xk+αuk)=0
解得
α = b T u k − x k T A u k u k T A u k \alpha = \frac{b^Tu_k - x_k^TAu_k}{u_k^TAu_k} α=ukTAukbTuk−xkTAuk
这里的 α \alpha α是最优步长的一个“尺度”,也就是scalar。那么问题来了,我们想要每次下降都能够是共轭方向的,怎么办呢?
设每次迭代之后的误差量为
r k = A x k − b r_k = Ax_k - b rk=Axk−b
令
u k = − r k + β k u k − 1 u_k = -r_k + \beta_k u_{k-1} uk=−rk+βkuk−1
两边乘以 u k − 1 T A u_{k-1}^TA uk−1TA有
u k − 1 T A u k = − u k − 1 T A r k + u k − 1 T A β k u k − 1 u_{k-1}^TAu_{k} = -u_{k-1}^TAr_k + u_{k-1}^TA\beta_ku_{k-1} uk−1TAuk=−uk−1TArk+uk−1TAβkuk−1
因为我们想要得到的是共轭方向,所以认为 u k − 1 T A u k = 0 u_{k-1}^TAu_{k} =0 uk−1TAuk=0
− u k − 1 T A r k + u k − 1 T A β k u k − 1 = 0 -u_{k-1}^TAr_k + u_{k-1}^TA\beta_ku_{k-1} = 0 −uk−1TArk+uk−1TAβkuk−1=0
β k = r k T A u k − 1 u k − 1 T A u k − 1 \beta_k= \frac{r_k^T A u_{k-1}}{u_{k-1}^TAu_{k-1}} βk=uk−1TAuk−1rkTAuk−1
在这里我们就可以得到一个缩放标量 β k \beta_k βk可以迭代计算共轭向量,最后得到的算法如下所示

优化线性共轭梯度法
进一步的,我们可以提出更高效的线性共轭梯度法。首先引入一些定理(这里的 p p p就是 u u u)

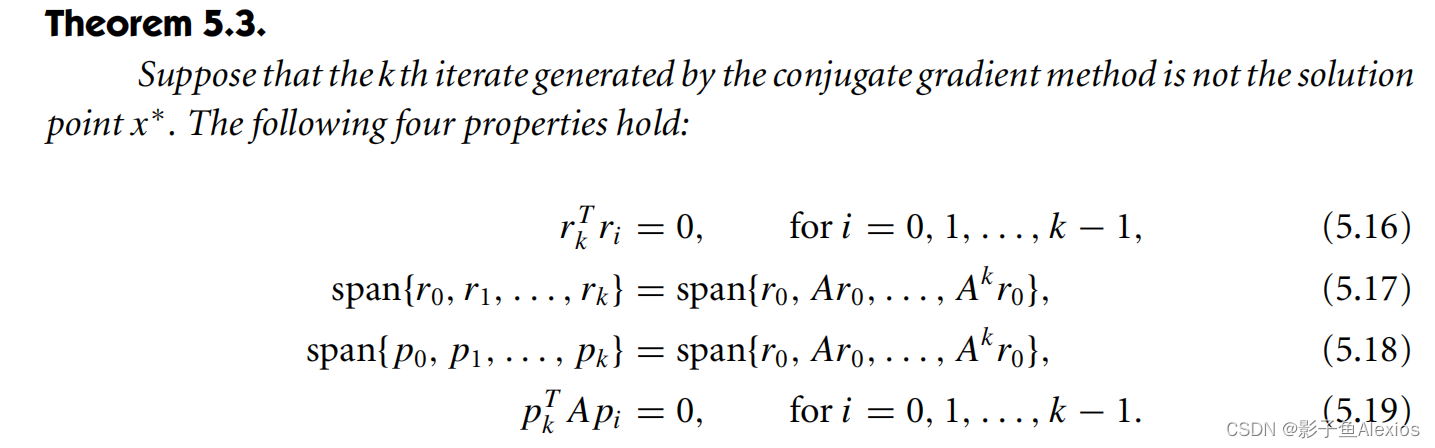
根据前面的公式,有
α = b T u k − x k T A u k u k T A u k = − r k T u k u k T A u k \alpha = \frac{b^Tu_k - x_k^TAu_k}{u_k^TAu_k} = \frac{-r_k^Tu_k}{u_k^TAu_k} α=ukTAukbTuk−xkTAuk=ukTAuk−rkTuk
由于 u k = − r k + β k u k − 1 u_k = -r_{k} + \beta_k u_{k-1} uk=−rk+βkuk−1
α = − r k T ( − r k + β u k − 1 ) u k T A u k \alpha = \frac{-r_k^T(-r_k+\beta u_{k-1})}{u_k^TA u_k} α=ukTAuk−rkT(−rk+βuk−1)
由于 r k T u k − 1 = 0 r_k^Tu_{k-1}=0 rkTuk−1=0
有
α k = r k T r k u k T A u k \alpha_k = \frac{r_k^Tr_k}{u_k^TA u_k} αk=ukTAukrkTrk
由于 α k A p k = r k + 1 − r k \alpha_kAp_k = r_{k+1}-r_k αkApk=rk+1−rk
继续代入有
β k + 1 = r k + 1 T r k + 1 r k T r k \beta_{k+1} = \frac{r_{k+1}^Tr_{k+1}}{r_{k}^Tr_{k}} βk+1=rkTrkrk+1Trk+1
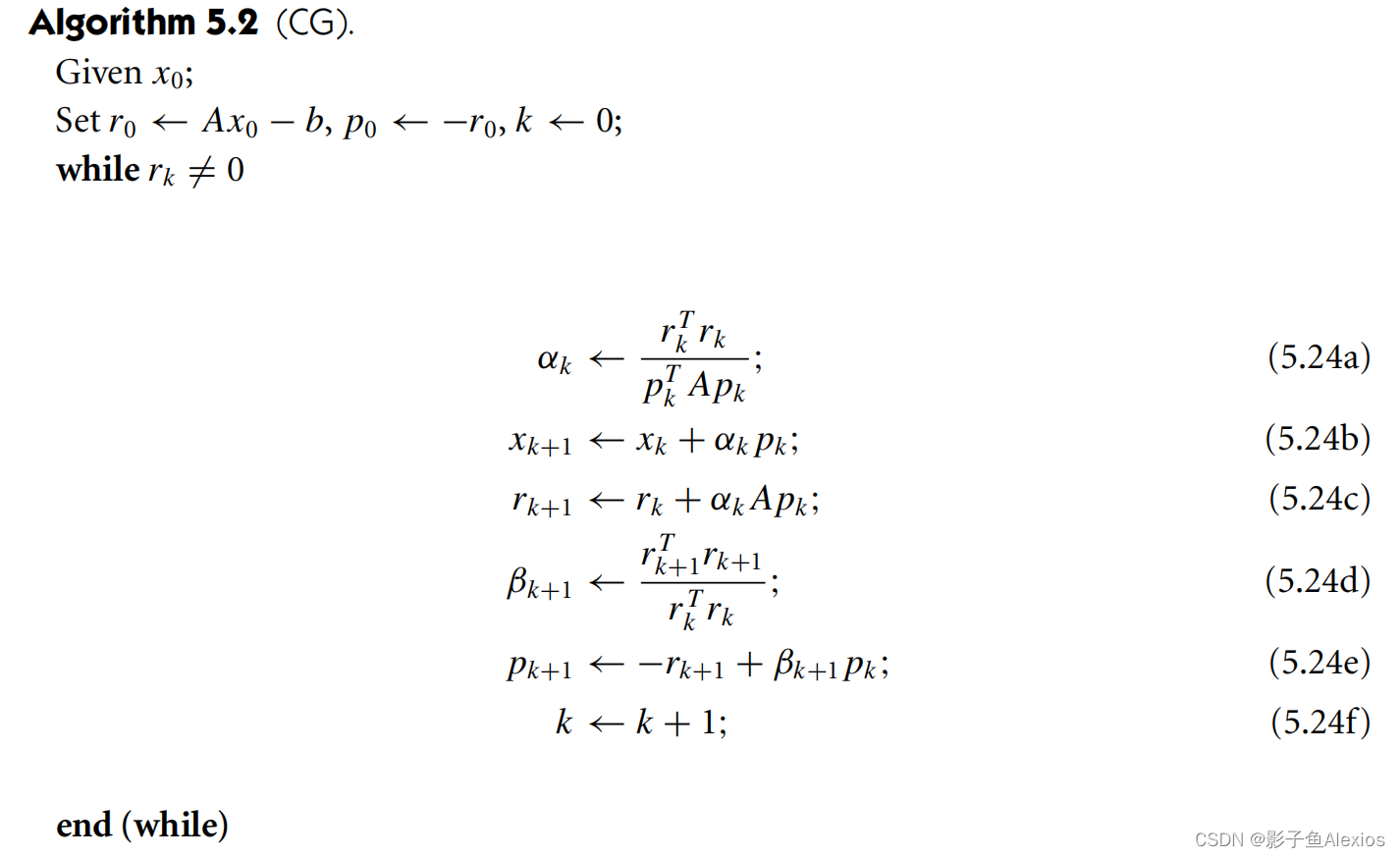
下一节中,将介绍牛顿共轭梯度法
相关文章:
机器人中的数值优化|【六】线性共轭梯度法,牛顿共轭梯度法
机器人中的数值优化|【六】线性共轭梯度法,牛顿共轭梯度法 往期回顾 机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例 机器人中的数值优化|【三】无约束优化…...
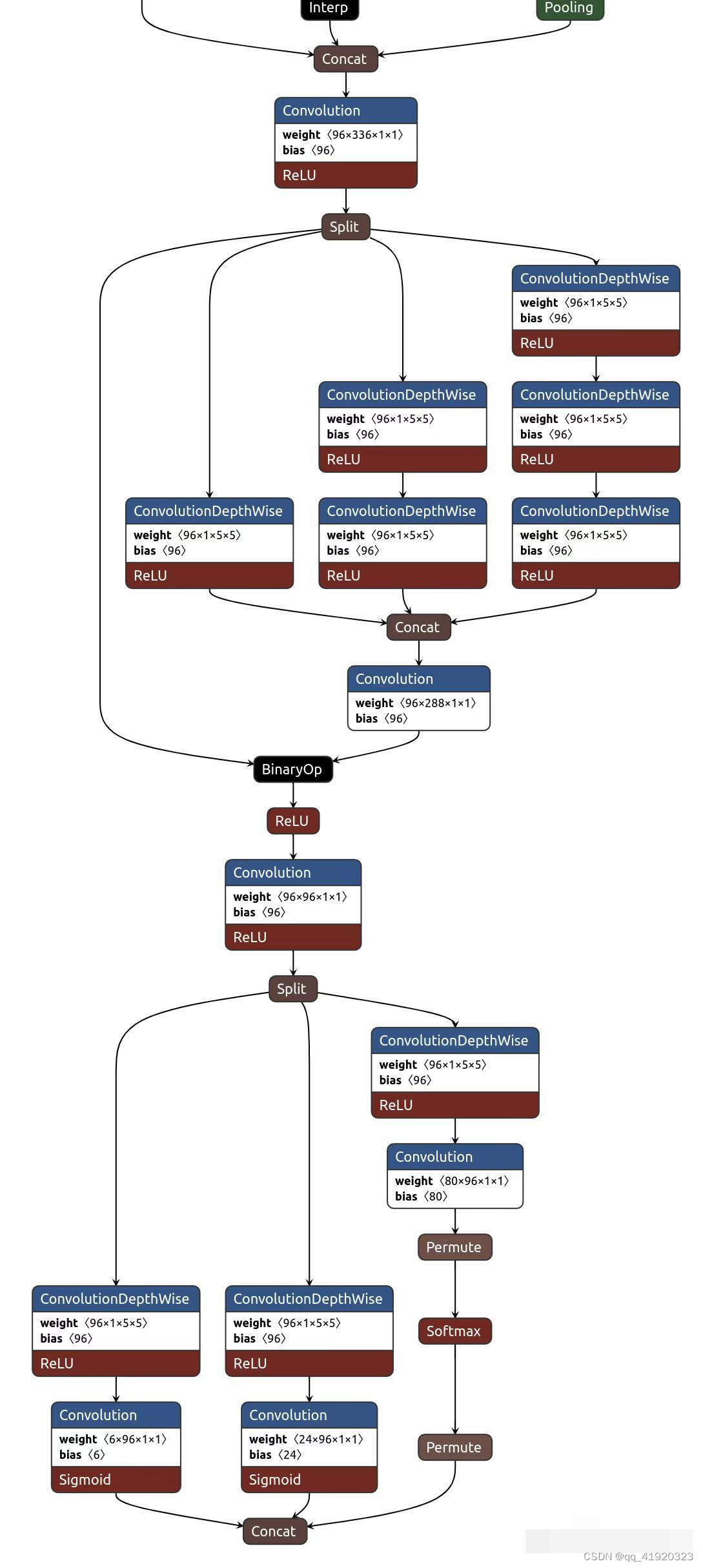
FastestDet---原理介绍
1.测试指标 2.算法定位 FastestDet是设计用来接替yolo-fastest系列算法,相比于业界已有的轻量级目标检测算法如yolov5n, yolox-nano, nanoDet, pp-yolo-tiny, FastestDet和这些算法根本不是一个量级,FastestDet无论在速度还是参数量上,都是要小好几个数量级的,但是精度自然…...
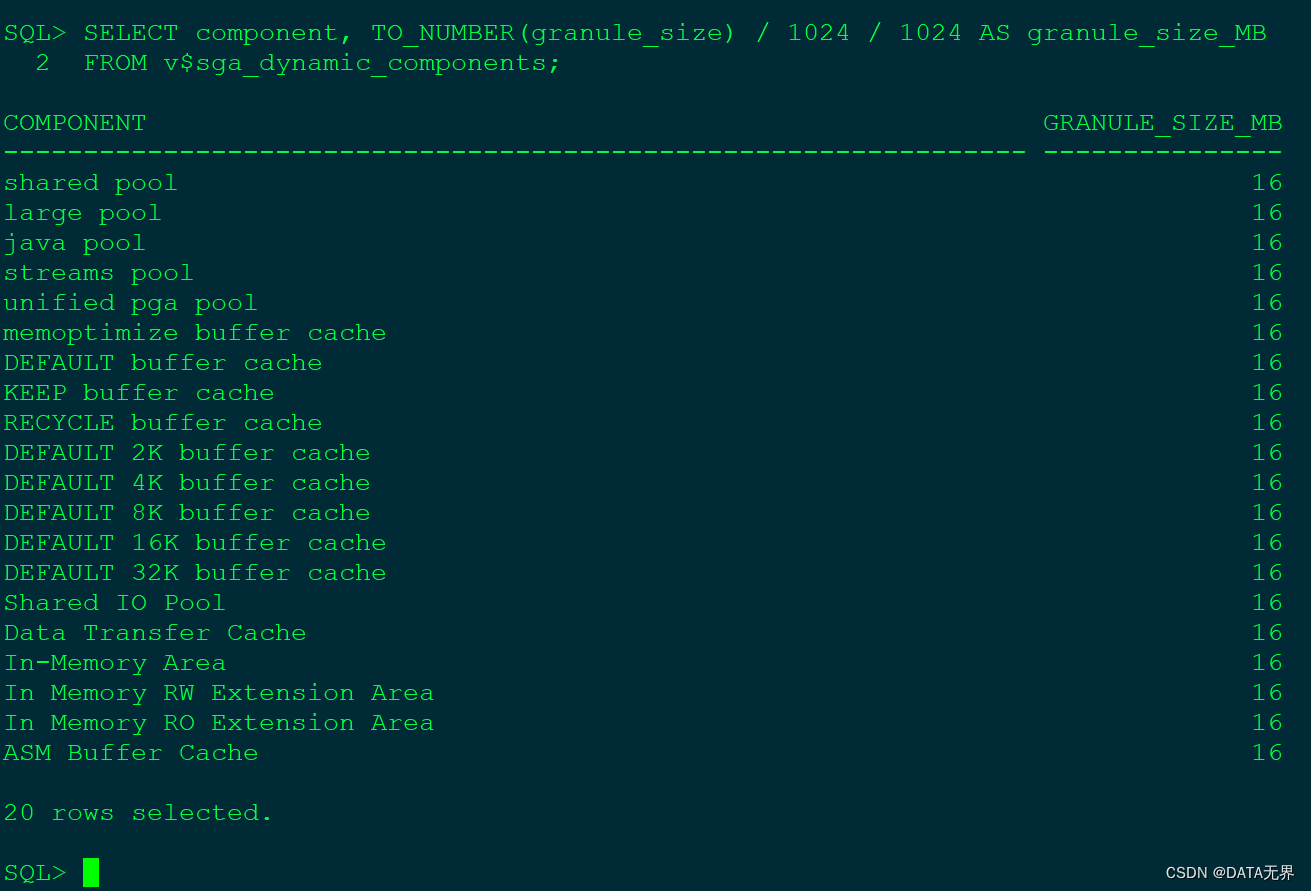
ORACLE 在内存管理机制上的演变和进化
截止目前,计算机内存仍然被认为是我们可以获得的最快速度的物理存储设备。 将频繁访问的数据尽可能地置于内存中,已成为当前各种软件和应用程序提高数据访问性能,减少访问延迟的最为有效的途径。 然而,内存作为关键的计算资源&am…...
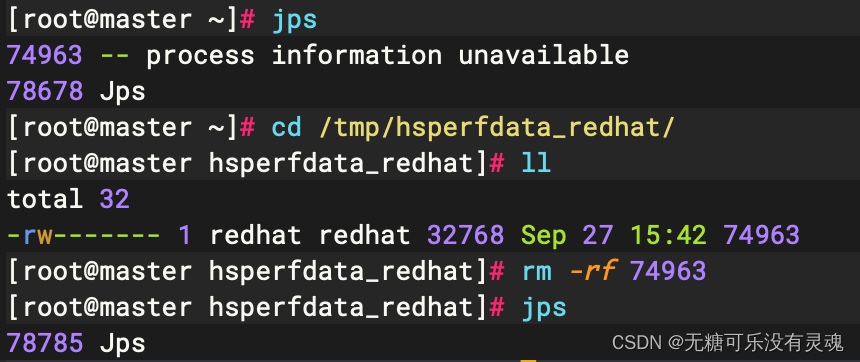
Linux ❀ 进程出现process information unavailable时的消除方法
[rootmaster ~]# jps 74963 -- process information unavailable 78678 Jps [rootmaster ~]# cd /tmp/hsperfdata_redhat/ # redhat为启动该java进程的用户ps -ef | grep $pid查找 [rootmaster hsperfdata_redhat]# ll total 32 -rw------- 1 redhat redhat 32768 Sep 27 15:…...
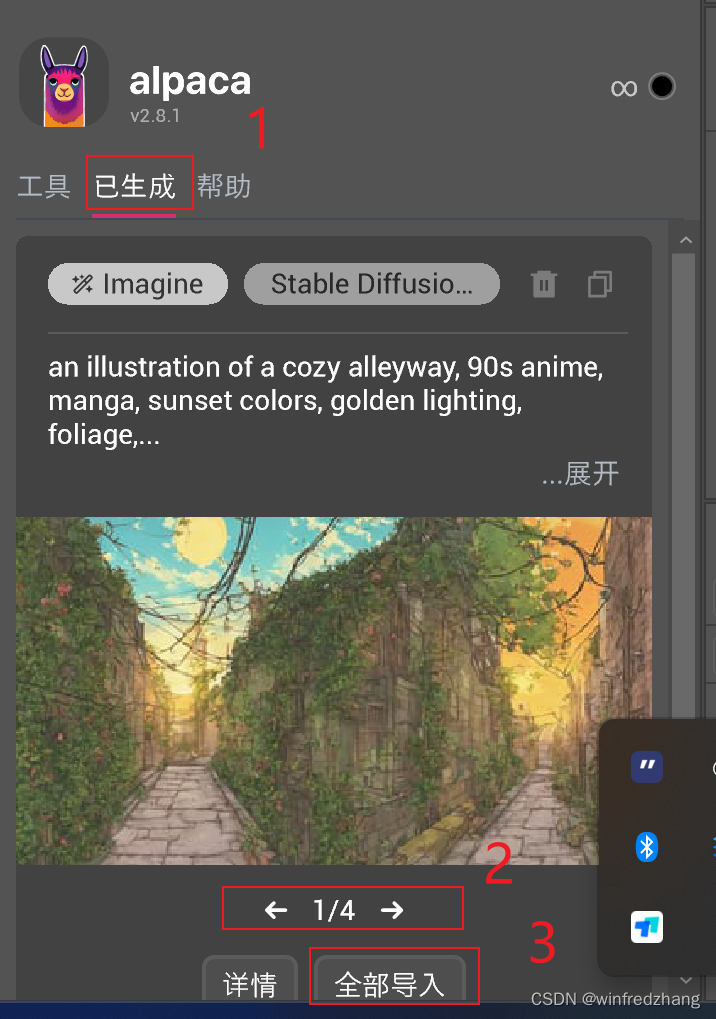
ps智能填充功能平替:alpaca的安装和使用
为了解决ps beta 智能填充无法使用的问题,需要用alpaca来平替,下面是安装教程: 安装方法: 1、下载插件。 alpaca插件汉化-夸克网盘https://pan.quark.cn/s/1168b447a44e#/list/share 2、 根据使用的PS版本,选择对应文件…...

【前端打怪升级日志之ES6篇】玩转函数
学习资料 阮一峰老师《ECMAScript 6 入门》— 函数的扩展 总结应用 1. 函数参数默认值与对象解构赋值默认值的结合使用 // 场景:方法调用时传参希望只传第二个参数 // 方案1: function foo({x1,y2}){console.log(x,y); } foo({}) //1 2 foo({x:2}) /…...
网址静态码手机制作教程,附图文详解!
网址的静态码是如何生成的呢?静态码是二维码的一种常用类型,一般常见的静态码类型主要是文本或者网址,那么在电脑制作静态码的方法相信很多小伙伴都知道怎么做,那么手机上制作的方法,大家感兴趣吗?下面来给…...
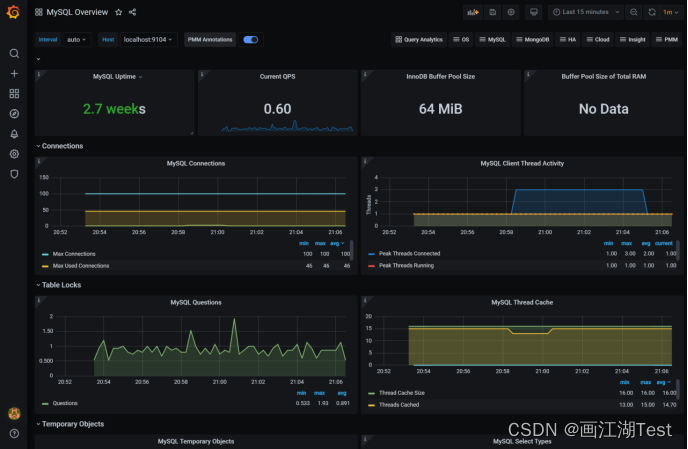
服务器性能测试监控平台export+prometheus(普罗米修斯)+grafana搭建
1. export 数据采集工具 简介: export是prometheus是的数据采集组件的总称,它可以将采集到的数据转为prometheus支持的格式 node_export: 用来监控服务器硬件资源的采集器,端口号为9100mysql_export: 用来监控mysql数据库资源的采集器&…...

【24种设计模式】责任链模式
责任链模式是一种行为设计模式,它允许你将请求沿着处理链进行传递,直到有一个处理者能够处理该请求为止。这种模式将请求的发送者和接收者解耦,使多个对象都有机会处理该请求。 责任链模式的结构 责任链模式由以下几个角色组成:…...

C#异步委托的三种实现 BeginInvoke / EndInvoke / IsCompleted
本文将介绍C#异步委托的三种实现方式,并给出相关示例代码及解析。 注意事项 用委托开启线程的前提是:创建项目时必须选择“.NET Framework",如果选择的是”.Net Core“,在调用BeginInvoke时,系统会报错”Operati…...

在HTTP请求中安全传输base64编码的字符串
前言 base64是一种常见的的编码格式,它可以把二进制数据编码成一个由大小写英文字母(a-zA-Z)、阿拉伯数字(0-9),以及三个特殊字符、/、组成的字符串。 问题 但是在URL传输中,、/、这三个特殊…...

05预测识别-依托YOLO V8进行训练模型的识别——对视频中的图片进行识别
在前面的一些章节中,我们已经讲如何准备打标签的素材、如何制作标签、如何训练以及得到我们最终需要的用于YOLO目标识别的模型。那么现在我们就要正式开始,利用我们训练得到的best.pt,这个模型文件来对图片视频进行识别。 1、基本思路 公安交管场景中,我们经常会遇到需要…...
LeetCode算法题---第3天
注:大佬解答来自LeetCode官方题解 121.买卖股票的最佳时期 1.题目 2.个人解答 function maxProfit(prices) {//更新最低价格和最大利润let minPrice prices[0];let maxProfit 0;for (let i 1; i < prices.length; i) {// 如果当前价格比最低价格还低,更新最…...

欧洲FBA专线海运与陆运的差别
随着全球电商市场的快速发展,越来越多的卖家选择将产品销售到欧洲市场。然而,面对欧洲境内的物流问题,卖家们往往会面临一个重要的选择:选择欧洲FBA专线时是选择海运还是陆运?这两种运输方式在时效、成本和服务质量上都有所不同&…...
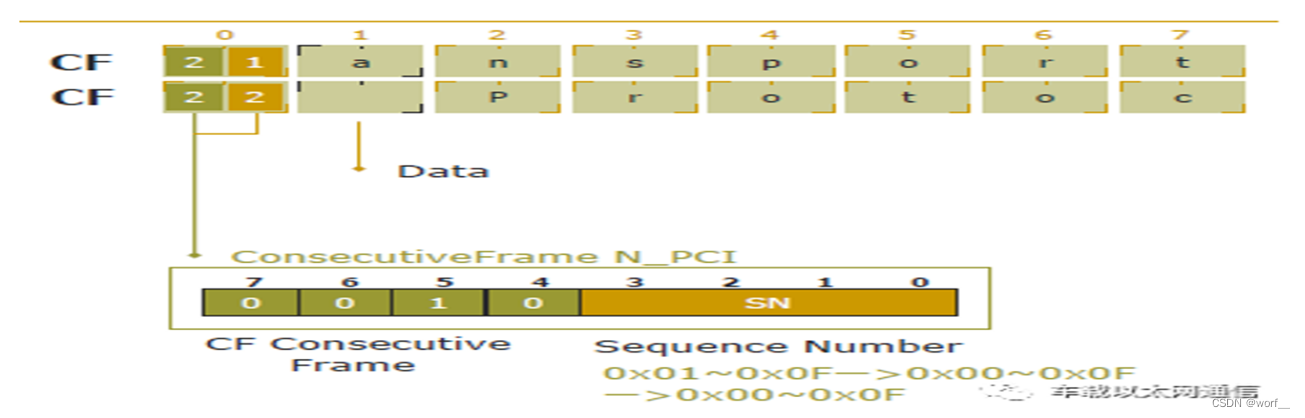
UDS诊断
一、UDS诊断简介 汽车诊断技术是指在不拆卸车辆的情况下,通过读取车辆在运行过程中所记录的数据或故障码来查明故障原因,并确定故障部位的汽车应用技术。通过诊断,可以快速检测到汽车故障来提高汽车安全性和维修效率。 USD协议诊断主要采用“…...

计算材料学学习记录1
计算材料学学习记录1 平台:Bohrium 老师:单斌教授 文章目录 1.发展史背景计算材料学 2.计算方法分类3.计算材料学的应用 1.发展史 背景 材料的研究方法发展: 一切靠实验理论开始起作用理论撑起半边天 “……解决全部化学的规律的数学方法…...

PHP8中的构造方法和析构方法-PHP8知识详解
今日分享的内容是php8中的构造方法和析构方法,我们把构造方法和析构方法这两个方法分开来讲: 1、构造方法 构造方法存在于每个声明的类中,主要作用是执行一些初始化任务。如果类中没有直接声明构造方法,那么类会默认地生成一个没…...
【GPU编程】Visual Studio创建基于GPU编程的项目
vs创建基于GPU编程的项目 🍊前言🐸方法一-CUDA Runtime生成😝debug设置 🍅方法二-空项目配置🍉🍉🍉代码验证 🍊前言 cuda以及cudnn的安装以及系统环境变量的配置默认已经做完。如果…...
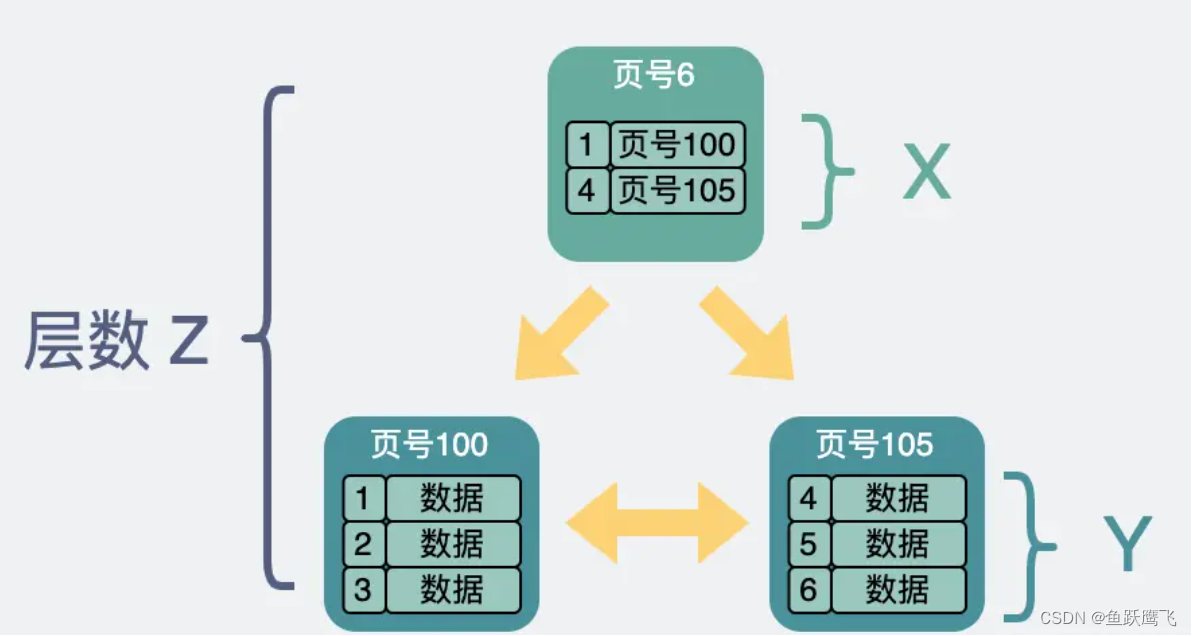
MySQL面试题-索引的基本原理及相关面试题
先了解一下MySQL的结构 下面我们重点讲一下存储引擎 MySQL的数据库和存储数据的目录是一一对应的,这些数据库的文件就保存在磁盘中对应的目录里 下面我们来看一下对应的具体数据文件 .frm是表的结构,不管什么样的索引都会有 .ibd代表我们现在使用的存…...
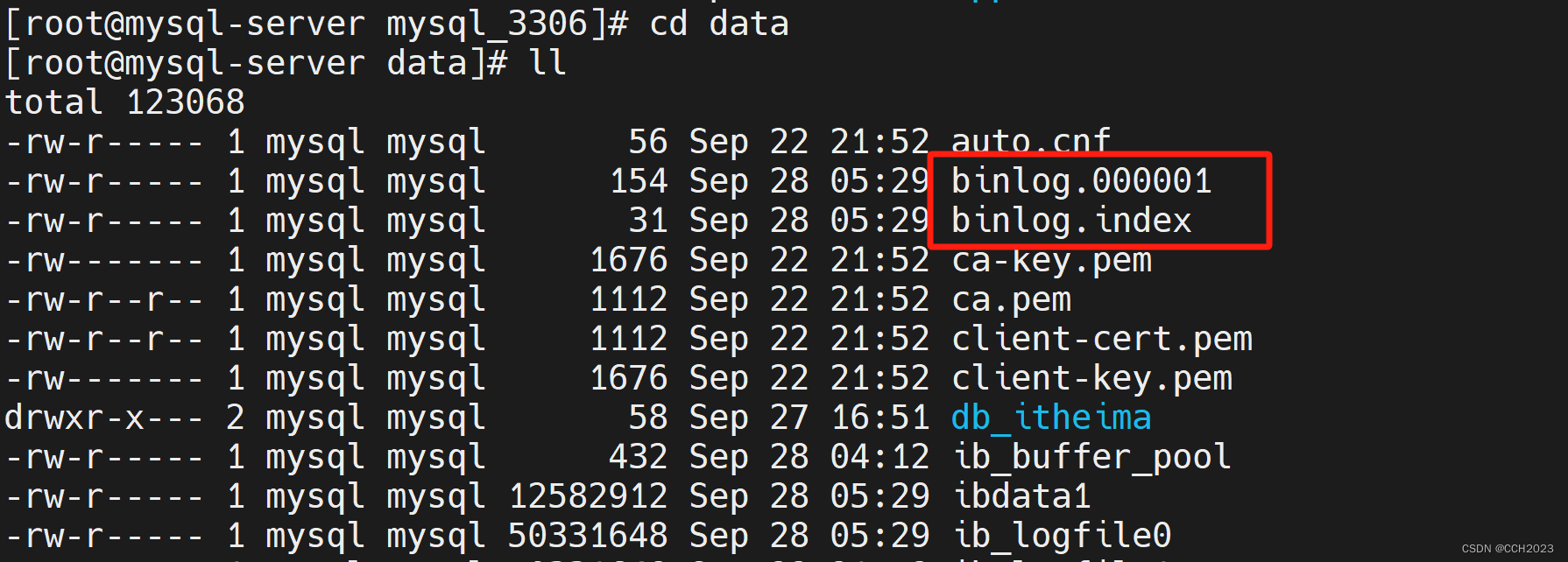
MySQL学习笔记19
MySQL日志文件:MySQL中我们需要了解哪些日志? 常见日志文件: 我们需要掌握错误日志、二进制日志、中继日志、慢查询日志。 错误日志: 作用:存放数据库的启动、停止和运行时的错误信息。 场景:用于数据库的…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
