算法与数据结构-Trie树
文章目录
- 什么是“Trie 树”?
- 如何实现一棵 Trie 树?
- Trie 树真的很耗内存吗?
- Trie 树与散列表、红黑树的比较
什么是“Trie 树”?
Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
当然,这样一个问题可以有多种解决方法,比如散列表、红黑树,或者我们前面几节讲到的一些字符串匹配算法,但是,Trie 树在这个问题的解决上,有它特有的优点。不仅如此,Trie 树能解决的问题也不限于此,我们一会儿慢慢分析。
现在,我们先来看下,Trie 树到底长什么样子。
我举个简单的例子来说明一下。我们有 6 个字符串,它们分别是:how,hi,her,hello,so,see。我们希望在里面多次查找某个字符串是否存在。如果每次查找,都是拿要查找的字符串跟这 6 个字符串依次进行字符串匹配,那效率就比较低,有没有更高效的方法呢?
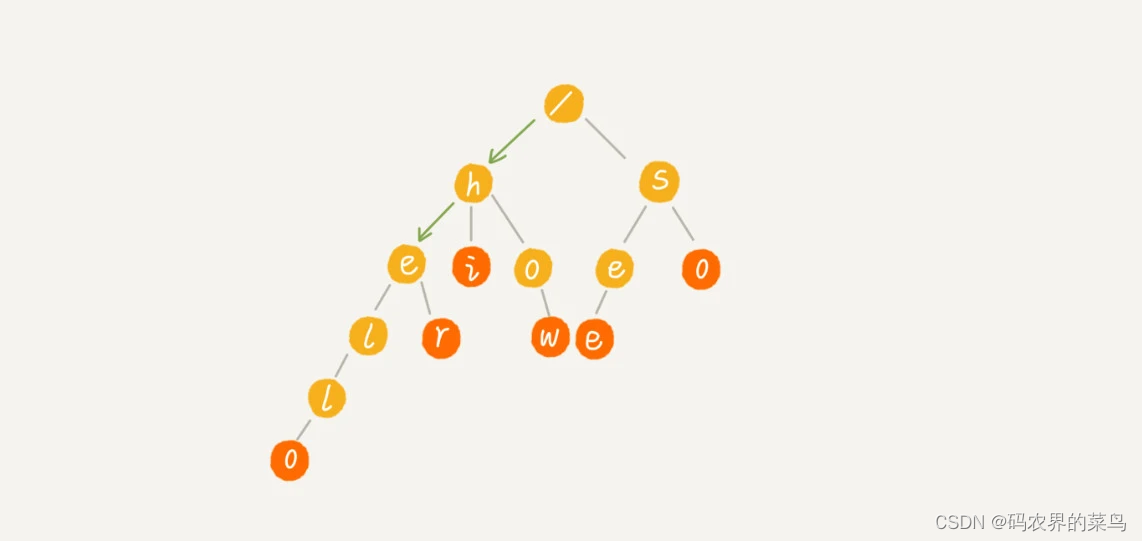
这个时候,我们就可以先对这 6 个字符串做一下预处理,组织成 Trie 树的结构,之后每次查找,都是在 Trie 树中进行匹配查找。Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。最后构造出来的就是下面这个图中的样子。
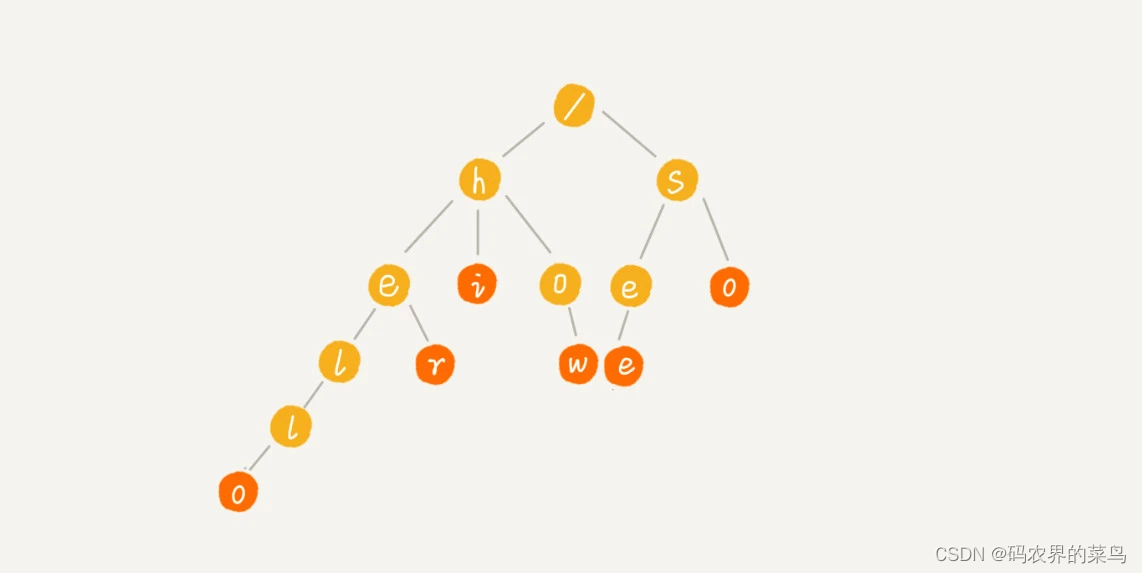
其中,根节点不包含任何信息。每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(注意:红色节点并不都是叶子节点)。
为了让你更容易理解 Trie 树是怎么构造出来的,我画了一个 Trie 树构造的分解过程。构造过程的每一步,都相当于往 Trie 树中插入一个字符串。当所有字符串都插入完成之后,Trie 树就构造好了。
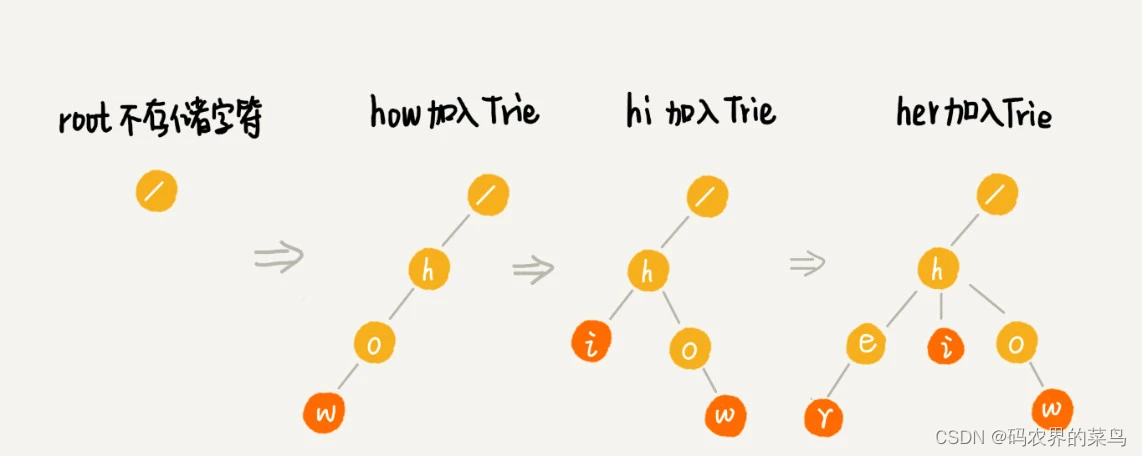
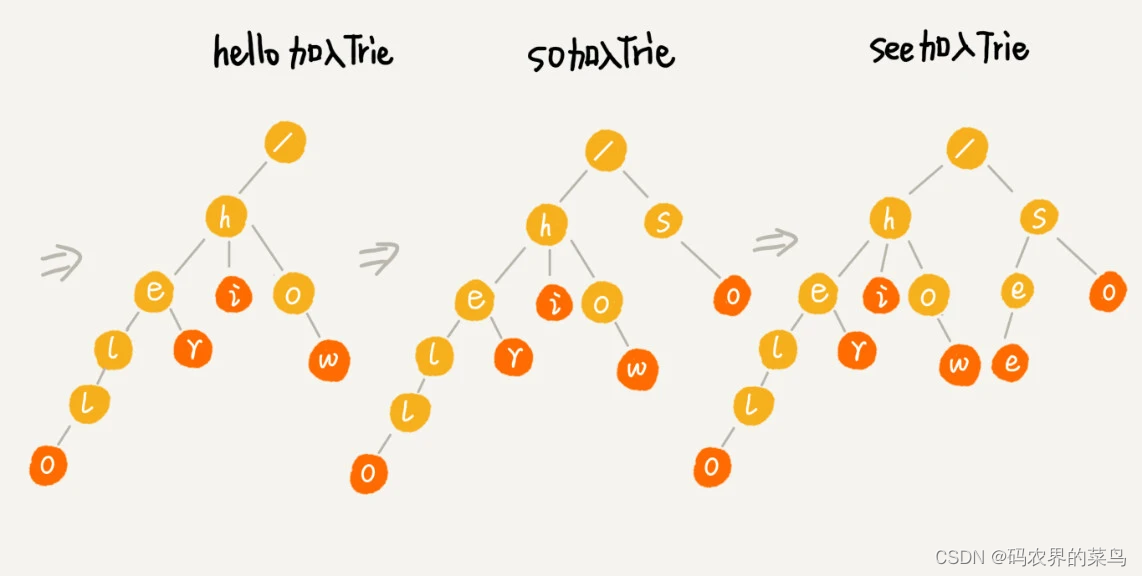
当我们在 Trie 树中查找一个字符串的时候,比如查找字符串“her”,那我们将要查找的字符串分割成单个的字符 h,e,r,然后从 Trie 树的根节点开始匹配。如图所示,绿色的路径就是在 Trie 树中匹配的路径。
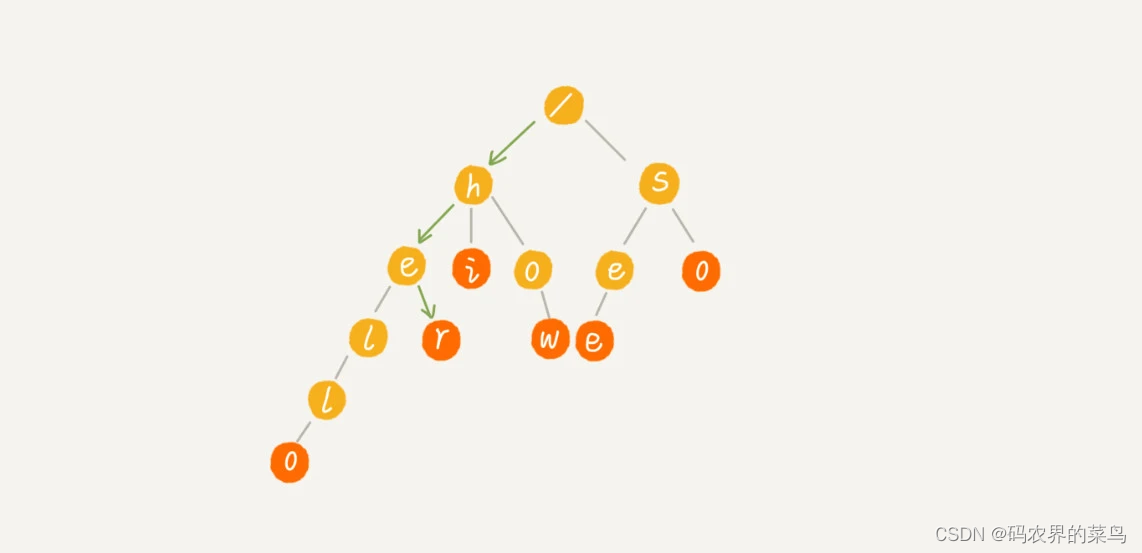
如果我们要查找的是字符串“he”呢?我们还用上面同样的方法,从根节点开始,沿着某条路径来匹配,如图所示,绿色的路径,是字符串“he”匹配的路径。但是,路径的最后一个节点“e”并不是红色的。也就是说,“he”是某个字符串的前缀子串,但并不能完全匹配任何字符串。
如何实现一棵 Trie 树?
知道了 Trie 树长什么样子,我们现在来看下,如何用代码来实现一个 Trie 树。
从刚刚 Trie 树的介绍来看,Trie 树主要有两个操作,一个是将字符串集合构造成 Trie 树。这个过程分解开来的话,就是一个将字符串插入到 Trie 树的过程。另一个是在 Trie 树中查询一个字符串。
了解了 Trie 树的两个主要操作之后,我们再来看下,如何存储一个 Trie 树?
从前面的图中,我们可以看出,Trie 树是一个多叉树。我们知道,二叉树中,一个节点的左右子节点是通过两个指针来存储的,如下所示 Java 代码。那对于多叉树来说,我们怎么存储一个节点的所有子节点的指针呢?
class BinaryTreeNode {char data;BinaryTreeNode left;BinaryTreeNode right;
}我先介绍其中一种存储方式,也是经典的存储方式,大部分数据结构和算法书籍中都是这么讲的。还记得我们前面讲到的散列表吗?借助散列表的思想,我们通过一个下标与字符一一映射的数组,来存储子节点的指针。这句话稍微有点抽象,不怎么好懂,我画了一张图你可以看看。
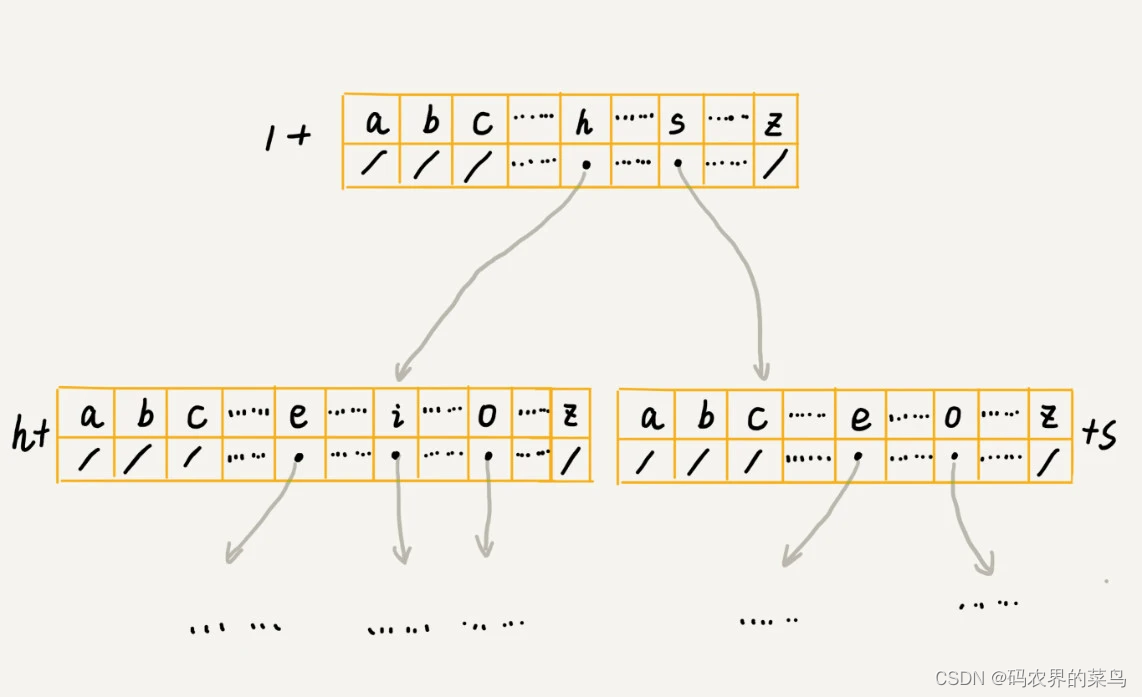
假设我们的字符串中只有从 a 到 z 这 26 个小写字母,我们在数组中下标为 0 的位置,存储指向子节点 a 的指针,下标为 1 的位置存储指向子节点 b 的指针,以此类推,下标为 25 的位置,存储的是指向的子节点 z 的指针。如果某个字符的子节点不存在,我们就在对应的下标的位置存储 null。
class TrieNode {char data;TrieNode children[26];
}
当我们在 Trie 树中查找字符串的时候,我们就可以通过字符的 ASCII 码减去“a”的 ASCII 码,迅速找到匹配的子节点的指针。比如,d 的 ASCII 码减去 a 的 ASCII 码就是 3,那子节点 d 的指针就存储在数组中下标为 3 的位置中。
描述了这么多,有可能你还是有点懵,我把上面的描述翻译成了代码,你可以结合着一块看下,应该有助于你理解。
public class Trie {private TrieNode root = new TrieNode('/'); // 存储无意义字符// 往Trie树中插入一个字符串public void insert(char[] text) {TrieNode p = root;for (int i = 0; i < text.length; ++i) {int index = text[i] - 'a';if (p.children[index] == null) {TrieNode newNode = new TrieNode(text[i]);p.children[index] = newNode;}p = p.children[index];}p.isEndingChar = true;}// 在Trie树中查找一个字符串public boolean find(char[] pattern) {TrieNode p = root;for (int i = 0; i < pattern.length; ++i) {int index = pattern[i] - 'a';if (p.children[index] == null) {return false; // 不存在pattern}p = p.children[index];}if (p.isEndingChar == false) return false; // 不能完全匹配,只是前缀else return true; // 找到pattern}public class TrieNode {public char data;public TrieNode[] children = new TrieNode[26];public boolean isEndingChar = false;public TrieNode(char data) {this.data = data;}}
}
Trie 树的实现,你现在应该搞懂了。现在,我们来看下,在 Trie 树中,查找某个字符串的时间复杂度是多少?
如果要在一组字符串中,频繁地查询某些字符串,用 Trie 树会非常高效。构建 Trie 树的过程,需要扫描所有的字符串,时间复杂度是 O(n)(n 表示所有字符串的长度和)。但是一旦构建成功之后,后续的查询操作会非常高效。
每次查询时,如果要查询的字符串长度是 k,那我们只需要比对大约 k 个节点,就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说,构建好 Trie 树后,在其中查找字符串的时间复杂度是 O(k),k 表示要查找的字符串的长度。
Trie 树真的很耗内存吗?
前面我们讲了 Trie 树的实现,也分析了时间复杂度。现在你应该知道,Trie 树是一种非常独特的、高效的字符串匹配方法。但是,关于 Trie 树,你有没有听过这样一种说法:“Trie 树是非常耗内存的,用的是一种空间换时间的思路”。这是什么原因呢?
刚刚我们在讲 Trie 树的实现的时候,讲到用数组来存储一个节点的子节点的指针。如果字符串中包含从 a 到 z 这 26 个字符,那每个节点都要存储一个长度为 26 的数组,并且每个数组元素要存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于 26 个,比如 3、4 个,我们也要维护一个长度为 26 的数组。
我们前面讲过,Trie 树的本质是避免重复存储一组字符串的相同前缀子串,但是现在每个字符(对应一个节点)的存储远远大于 1 个字节。按照我们上面举的例子,数组长度为 26,每个元素是 8 字节,那每个节点就会额外需要 26*8=208 个字节。而且这还是只包含 26 个字符的情况。
如果字符串中不仅包含小写字母,还包含大写字母、数字、甚至是中文,那需要的存储空间就更多了。所以,也就是说,在某些情况下,Trie 树不一定会节省存储空间。在重复的前缀并不多的情况下,Trie 树不但不能节省内存,还有可能会浪费更多的内存。
当然,我们不可否认,Trie 树尽管有可能很浪费内存,但是确实非常高效。那为了解决这个内存问题,我们是否有其他办法呢?
我们可以稍微牺牲一点查询的效率,将每个节点中的数组换成其他数据结构,来存储一个节点的子节点指针。用哪种数据结构呢?我们的选择其实有很多,比如有序数组、跳表、散列表、红黑树等。
假设我们用有序数组,数组中的指针按照所指向的子节点中的字符的大小顺序排列。查询的时候,我们可以通过二分查找的方法,快速查找到某个字符应该匹配的子节点的指针。但是,在往 Trie 树中插入一个字符串的时候,我们为了维护数组中数据的有序性,就会稍微慢了点。
实际上,Trie 树的变体有很多,都可以在一定程度上解决内存消耗的问题。比如,缩点优化,就是对只有一个子节点的节点,而且此节点不是一个串的结束节点,可以将此节点与子节点合并。这样可以节省空间,但却增加了编码难度。这里我就不展开详细讲解了,你如果感兴趣,可以自行研究下。

Trie 树与散列表、红黑树的比较
实际上,字符串的匹配问题,笼统上讲,其实就是数据的查找问题。对于支持动态数据高效操作的数据结构,我们前面已经讲过好多了,比如散列表、红黑树、跳表等等。实际上,这些数据结构也可以实现在一组字符串中查找字符串的功能。我们选了两种数据结构,散列表和红黑树,跟 Trie 树比较一下,看看它们各自的优缺点和应用场景。
在刚刚讲的这个场景,在一组字符串中查找字符串,Trie 树实际上表现得并不好。它对要处理的字符串有极其严苛的要求。
- 第一,字符串中包含的字符集不能太大。我们前面讲到,如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
- 第二,要求字符串的前缀重合比较多,不然空间消耗会变大很多。
- 第三,如果要用 Trie 树解决问题,那我们就要自己从零开始实现一个 Trie 树,还要保证没有 bug,这个在工程上是将简单问题复杂化,除非必须,一般不建议这样做。
- 第四,我们知道,通过指针串起来的数据块是不连续的,而 Trie 树中用到了指针,所以,对缓存并不友好,性能上会打个折扣。
综合这几点,针对在一组字符串中查找字符串的问题,我们在工程中,更倾向于用散列表或者红黑树。因为这两种数据结构,我们都不需要自己去实现,直接利用编程语言中提供的现成类库就行了。
实际上,Trie 树只是不适合精确匹配查找,这种问题更适合用散列表或者红黑树来解决。Trie 树比较适合的是查找前缀匹配的字符串,也就是类似开篇问题的那种场景。
相关文章:

算法与数据结构-Trie树
文章目录 什么是“Trie 树”?如何实现一棵 Trie 树?Trie 树真的很耗内存吗?Trie 树与散列表、红黑树的比较 什么是“Trie 树”? Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符…...
)
语音助手开发小记(2023.9.25)
通道问题 在使用函数swr_alloc_set_opts给SwrContext传递输入输出的音频参数时,需要设置通道,这里通道为2,但是通道布局不能传递2.比如AV_CH_LAYOUT_STEREO 实际值为3 如果要计算通道布局的通道数使用函数av_get_channel_layout_nb_channels…...
FastestDet---模型训练
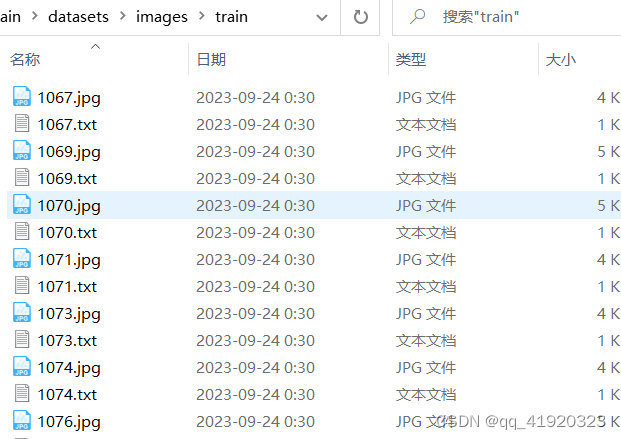
代码:https://github.com/dog-qiuqiu/FastestDet 一、构造数据集 数据集格式YOLO相同,每张图片对应一个txt标签文件。标签格式:“category cx cy wh”,category为类别id,cx, cy为归一化标签框中心点的坐标,w, h为归一化标签框的宽度和高度, .txt标签文件内容示例如下: 0…...
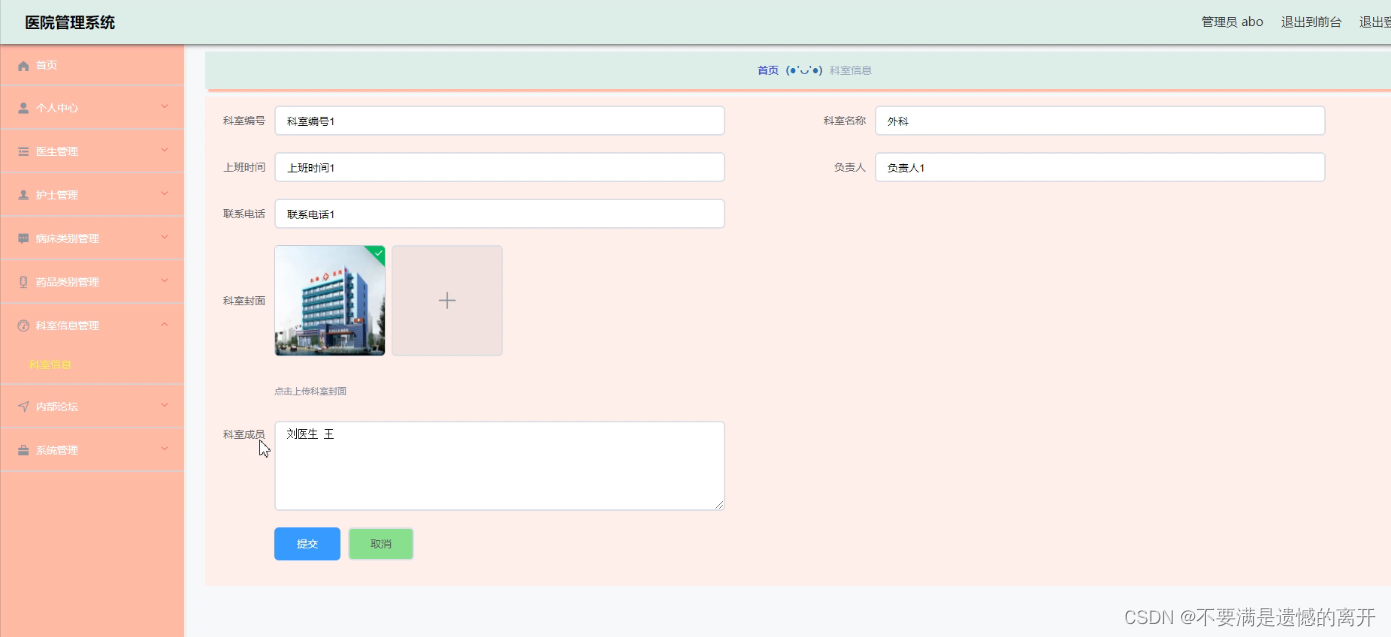
基于SpringBoot的医院管理系统
目录 前言 一、技术栈 二、系统功能介绍 病床信息管理 药房信息管理 个人中心管理 药房信息 病床类别 科室信息管理 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 随着信息互联网信息的飞速发展,医院也在创建着属于自己的管理系统。本文介…...

java图片转pdf ,pdf 导出
pom引入jar <dependency><groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>2.0.0-RC2</version></dependency> 转pdf方法 /*** 使用pdfbox将jpg转成pdf** throws IOException IOException*/pu…...

掌握Go的运行时:从编译到执行
目录 一、Go运行编译简介Go语言的目标和设计哲学运行时环境编译过程小结 二、执行环境操作系统与硬件层系统调用(Syscalls)虚拟内存 Go运行时(Runtime)Goroutine调度器内存管理和垃圾收集网络I/O代码示例:Go运行时调度…...

打造香港最安全便捷的银行,众安银行发布首份技术白皮书
作者:林海宾&李龙 作为香港金融科技的代表,香港虚拟银行通过科技驱动,为客户提供了安全、便捷、普惠的金融服务。在八间持牌的虚拟银行中,众安银行目前在用户数量、存款、资产和收入规模上均处于领先水平。最快120秒线上开户…...

Spring实现简单的Bean容器
1.BeanDefinition,用于定义 Bean 实例化信息,现在的实现是以一个 Object 存放对象 public class BeanDefinition {/*** bean对象*/private Object bean;/*** 存放 (定义)Bean 对象*/public BeanDefinition(Object bean) {this.bea…...

Python15题day13
③continue的好处 break是跳出循环体,continue是跳过continue语句后面的代码块,循环并不停止 题目要求: 使用input函数接受用户的输入,如果用户输入的数值小于等于10,则判断是奇数还是偶数如果数值大于10,则输出“输入…...
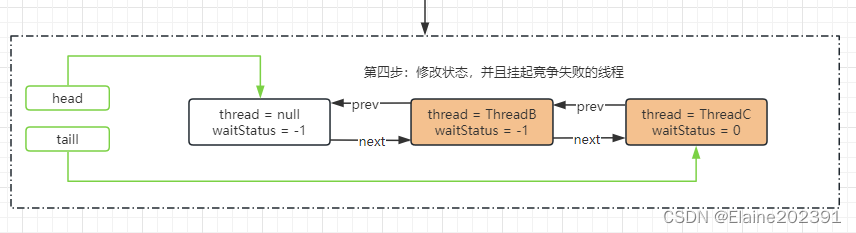
聊聊并发编程——多线程之AQS
目录 队列同步器(AQS) 独占锁示例 AQS之同步队列结构 解析AQS实现 队列同步器(AQS) 队列同步器AbstractQueuedSynchronizer(以下简称同步器),是用来构建锁或者其他同步组 件的基础框架&…...
DE0开发板交通灯十字路口红绿灯VHDL
名称:基于DE0开发板的交通灯十字路口红绿灯 软件:Quartus 语言:VHDL 要求: 设计一个十字路口交通信号灯的控制电路。分为两种情况,正常状态和报警状态。 1.正常状态:要求红、绿灯按一定的规律亮和灭&a…...
华为云云耀云服务器L实例评测使用 | 通过程序实现直播流自动分段录制
华为云云耀云服务器L实例评测使用 | 通过程序实现直播流自动分段录制 1. 准备工作2. 环境搭建3. 心得总结 1. 准备工作 随着云计算时代的进一步深入,越来越多的中小企业企业与开发者需要一款简单易用、高能高效的云计算基础设施产品来支撑自身业务运营和创新开发。基…...

前端教程-webpack
官网 webpack webpack基础 视频教程 尚硅谷Webpack5入门到原理(面试开发一条龙)...
)
white-space几种属性的用法(处理空格)
white-space:normal 文首的空格忽略,文本内部的换行符自动转成了空格。 white-space:nowrap 不换行,即使超出容器宽度 white-space:pre 与原文本一致,空格和换行符保留 white-space:pre-…...

Linux的历史
Linux的历史 前言: 关于Linux,你可能只是听说过它是一款操作系统,也许你还知道它是开源的,但在日常生活中,你更熟悉的是Windows。 那么我们为什么要了解、学习Linux,看完这一篇,你也许可以从…...

软考高级系统架构设计师系列论文真题八:论企业集成平台的技术与应用
软考高级系统架构设计师系列论文真题八:论企业集成平台的技术与应用 一、论企业集成平台的技术与应用二、找准核心论点三、理论素材准备四、精品范文赏析1.摘要2.正文3.总结软考高级系统架构设计师系列论文之:百篇软考高级架构设计师论文范文软考高级系统架构设计师系列之:论…...

[H5动画制作系列] 路径引导动画 Demo
代码参考1: <!DOCTYPE html> <html lang="en"><head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><title>路径引导动画 Demo1</tit…...
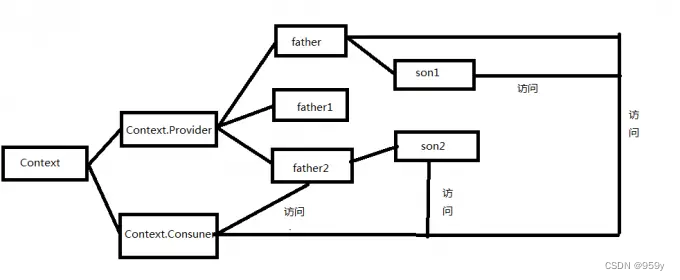
[React] Context上下文的使用
文章目录 1.Context的介绍2.为什么需要Context3.Context的使用 1.Context的介绍 Context旨在为React复杂嵌套的各个组件提供一个生命周期内的统一属性访问对象,从而避免我们出现当出现复杂嵌套结构的组件需要一层层通过属性传递值得问题。 Context是为了提供一个组…...
:cmd-parser串口命令解析器移植)
高云FPGA系列教程(9):cmd-parser串口命令解析器移植
文章目录 @[toc]cmd-parser库简介cmd-parser库源码获取GW1NSR-4C移植cmd-parser实际测试cmd-parse命令解析器优化本文是高云FPGA系列教程的第9篇文章。 上一篇文章介绍片上ARM Cortex-M3硬核处理器串口外设的使用,演示轮询方式和中断方式接收串口数据,并进行回环测试。 本文…...

PHP8的静态变量和方法-PHP8知识详解
我们在上一课程讲到了public、private、protected这3个关键字,今天我们来讲解static关键字,明天再讲解final关键字。 如果不想通过创建对象来调用变量或方法,则可以将该变量或方法创建为静态变量或方法,也就是在变量或方法的前面…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
