估计、偏差和方差
一、介绍
统计领域为我们提供了很多工具来实现机器学习目标,不仅可以解决训练集上的任务,还可以泛化。基本的概念,例如参数估计、偏差和方差,对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。
二、参数估计
参数估计 是统计学中的一个关键概念,它涉及估计概率分布中的参数值,以便能够对总体或随机过程进行描述或预测。参数估计通常分为两个主要类型:点估计和区间估计。
-
点估计(Point Estimation):
- 点估计旨在找到单个值,该值代表未知参数的“最佳猜测”。这个值通常是一个统计样本的函数。
- 常见的点估计方法包括最大似然估计(Maximum Likelihood Estimation,MLE)和最小二乘估计(Least Squares Estimation),它们都用于估计参数值。
- 例如,如果你想估计某个总体的均值或方差,样本均值和样本方差可以分别用作点估计。
-
区间估计(Interval Estimation):
- 区间估计涉及到估计参数值的范围,而不是单个点。这个范围通常以置信区间的形式表示。
- 置信区间告诉你参数值落在一个特定的区间内的概率有多大。典型的置信水平是95%,这意味着在多次抽样中,大约95%的区间会包含真实参数值。
- 区间估计提供了估计的不确定性度量,相比于点估计更具信息量
三、点估计
点估计(Point Estimation) 是统计学中的一种方法,用于估计未知参数的单个值,通常是一个统计样本的函数。点估计的目标是找到一个估计值,该估计值可以代表未知参数的"最佳猜测",尽管它可能不会精确地等于真实参数值。

点估计涉及以下关键概念:
-
参数: 在统计学中,参数是描述总体分布或概率分布的特征,例如均值、方差、概率等。点估计的目标通常是估计这些参数的值。
-
估计量: 估计参数值的统计量被称为估计量。估计量通常是基于样本数据计算的函数,用于估计总体参数。
-
点估计值: 点估计值是估计量的具体值,它代表了对参数的估计。这是一个单个数值,通常是样本数据的函数。
点估计的常见例子包括:
-
样本均值估计总体均值: 如果你想估计某个总体的均值,可以使用样本均值作为点估计,即将样本数据的平均值作为总体均值的估计值。
-
样本方差估计总体方差: 如果你希望估计总体的方差,可以使用样本方差作为点估计,即将样本数据的方差作为总体方差的估计值。
-
二项分布的成功概率估计: 如果你想估计二项分布中成功的概率(例如投硬币正面的概率),可以使用成功的样本比例作为点估计。
需要注意的是,点估计提供了对参数的单个估计值,但并不提供关于估计的精确性或可信度的信息。为了更全面地了解估计的可信度,通常还会进行区间估计和假设检验等进一步的统计分析。点估计在统计学中是一个基础而重要的概念,它为估计未知参数提供了一种简单而直观的方法。
三、常用的点估计方法
常用的点估计方法有以下几种:
1. 最大似然估计(Maximum Likelihood Estimation, MLE):基于样本数据的概率分布模型,寻找参数值,使得给定样本观测到的概率最大。
2. 最小二乘估计(Least Squares Estimation, LSE):通过最小化样本观测值与模型预测值之间的平方差,来估计参数值。
3. 矩估计法(Method of Moments, MOM):通过将样本矩与理论矩相等,来求解参数的估计值。
4. 贝叶斯估计(Bayesian Estimation):基于贝叶斯定理,结合先验信息和样本信息,得到参数的后验分布,并通过后验分布来进行参数估计。
四、偏差
在统计学中,偏差是指参数估计的期望值与真实参数值之间的差异。简而言之,它表示估计值在平均情况下离真实值有多远。一个无偏的估计是指其期望值等于真实参数值。如果估计的期望值与真实值有偏差,那么这个估计就是有偏的。有偏估计在某些情况下可能更准确,但在其他情况下可能不准确。


五、方差和标准差
方差(Variance) 和 标准差(Standard Deviation) 都是用于衡量数据分布或随机变量离散程度的统计指标,它们之间有密切的关系。
-
方差是一组数据的离散程度的度量,它表示数据点与数据集均值之间的差异程度的平方平均值。方差越大,表示数据点更分散,离均值越远。
-
标准差是方差的平方根,它衡量了数据的离散程度,但以与原始数据相同的单位来表示。标准差通常更容易理解,因为它与原始数据的尺度一致。
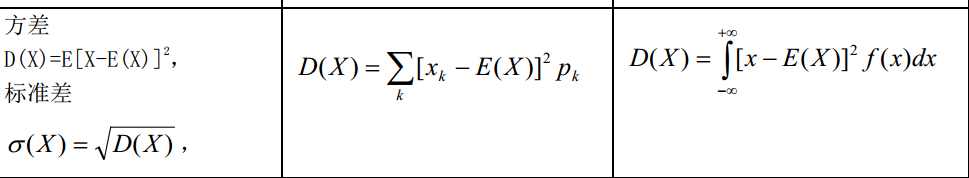
方差和标准差的应用:
-
方差和标准差常用于描述数据的离散程度。如果数据的方差或标准差较大,说明数据点分布较分散;如果它们较小,说明数据点较接近均值。
-
在统计学和机器学习中,方差和标准差用于衡量模型的性能和稳定性。例如,模型的预测误差的方差可以用来评估模型的稳定性,较小的方差表示模型更一致地预测。
参考:
概率论:参数估计——点估计_李小星同志的博客-CSDN博客
《统计推断》整理3:点估计 - 知乎
相关文章:
估计、偏差和方差
一、介绍 统计领域为我们提供了很多工具来实现机器学习目标,不仅可以解决训练集上的任务,还可以泛化。基本的概念,例如参数估计、偏差和方差,对于正式地刻画泛化、欠拟合和过拟合都非常有帮助。 二、参数估计 参数估计 是统计学…...
正态分布的概率密度函数|正态分布检验|Q-Q图
正态分布的概率密度函数(Probability Density Function,简称PDF)的函数取值是指在给定的正态分布参数(均值 μ 和标准差 σ)下,对于特定的随机变量取值 x,计算得到的概率密度值 f(x)。这个值表示…...
【接口测试】HTTP协议
一、HTTP 协议基础 HTTP 简介 HTTP 是一个客户端终端(用户)和服务器端(网站)请求和应答的标准(TCP)。通常是由客户端发起一个请求,创建一个到服务器的 TCP 连接,当服务器监听到客户…...
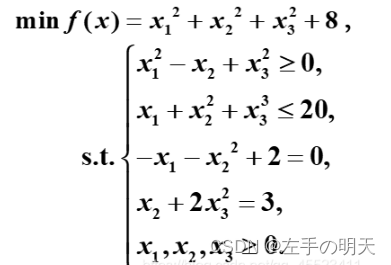
【重新定义matlab强大系列十四】基于问题求解有/无约束非线性优化
🔗 运行环境:Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### 💗 大家好🤗ᾑ…...

MySQL 索引介绍和最佳实践
目录 一、前言二、索引类型1.1 主键索引(PRIMARY KEY)1.2 唯一索引(UNIQUE)1.3 普通索引(NORMAL)1.3.1 单列普通索引1.3.2 单列前缀普通索引1.3.3 多列普通索引1.3.4 多列前缀普通索引 1.4 空间索引&#x…...
:p2p去中心化之初始化websoket服务端)
区块链(7):p2p去中心化之初始化websoket服务端
1 整个流程梳理 服务开启onStart()连接打开onOpen()处理接收到的消息onMesage()连接关闭onClose()异常处理onError()2 创建p2p实现类 package com.example.demo.service;import com.example.demo.entity.BlockChain; import org.java_websocket.WebSocket; import org.java_we…...

原型、原型链、判断数据类型
目录 作用 原型链 引用类型:__proto__(隐式原型)属性,属性值是对象函数:prototype(原型)属性,属性值是对象 Function:本身也是函数 相关方法 person.prototype.isPrototypeOf(stu) Object.getPrototypeOf(objec…...
pycharm中配置torch
在控制台cmd中安装好torch后,在pycharm中使用torch,需要进行简单设置即可。 在pycharm中新建一个工程,在file文件中打开setting 在setting中找到project interpreter编译器 找到conda environment的环境配置,设置好相应的目录 新…...
什么是Times New Roman 字体
如何评价 Times New Roman 字体?:https://www.zhihu.com/question/24614549?sortcreated 新罗马字体是Times New Roman字体,是Office Word默认自带的英文字体之一。 中英文字体 写作中,英文和数字的标准字体为 Times New Roma…...

企业会议新闻稿怎么写?会议类新闻稿如何撰写?
企业会议新闻稿是企业对外传递信息的重要途径之一,它能够将企业的决策、动态以及成果展示给公众。本文伯乐网络传媒将详细解析企业会议新闻稿的写作要点和技巧,以及常见问题及解决方法,帮助大家更好地完成企业会议新闻稿的撰写工作。 一、企业…...
)
算法 滑动窗口最大值-(双指针+队列)
牛客网: BM45 题目: 数组num, 窗口大小size, 所有窗口内的最大值 思路: 用队列作为窗口,窗口内存储数组坐标,left window[0], right从数组0开始遍历完数组,每次新增元素时,(1)先对窗口大小进行收缩到size大小范围,即…...

Java 并发编程面试题——BlockingQueue
目录 1.什么是阻塞队列 (BlockingQueue)?2.BlockingQueue 有哪些核心方法?3.BlockingQueue 有哪些常用的实现类?3.1.ArrayBlockingQueue3.2.DelayQueue3.3.LinkedBlockingQueue3.4.PriorityBlockingQueue3.5.SynchronousQueue 4.✨BlockingQu…...

Ubuntu Nacos开机自启动服务
1、创建service文件 在/lib/systemd/system目录下创建nacos.service文件 [Unit] Descriptionalibaba nacos Afternetwork.target Documentationhttps://nacos.io/zh-cn/[Service] Userroot Grouproot Typeforking Environment"JAVA_HOME/usr/local/programs/jdk-8u333-li…...

C++核心编程--继承篇
4.6、继承 继承是面向对象三大特征之一 有些类与类之间存在特殊的关系,例如下图中: 我们发现,定义这些类的定义时,都拥有上一级的一些共性,还有一些自己的特性。那么我们遇到重复的东西时,就可以考虑使…...

小程序 解决自定义弹窗滚动穿透问题,解决弹窗背景内容滚动问题
方法一、catchtouchmove"true", 可以实现弹框背景不滚动,但是也会导致弹框自身无法滚动,如果你的弹窗本身是不需要滚动的,用这个方法是极佳的。 <view class"pop" catchtouchmove"true"> …...
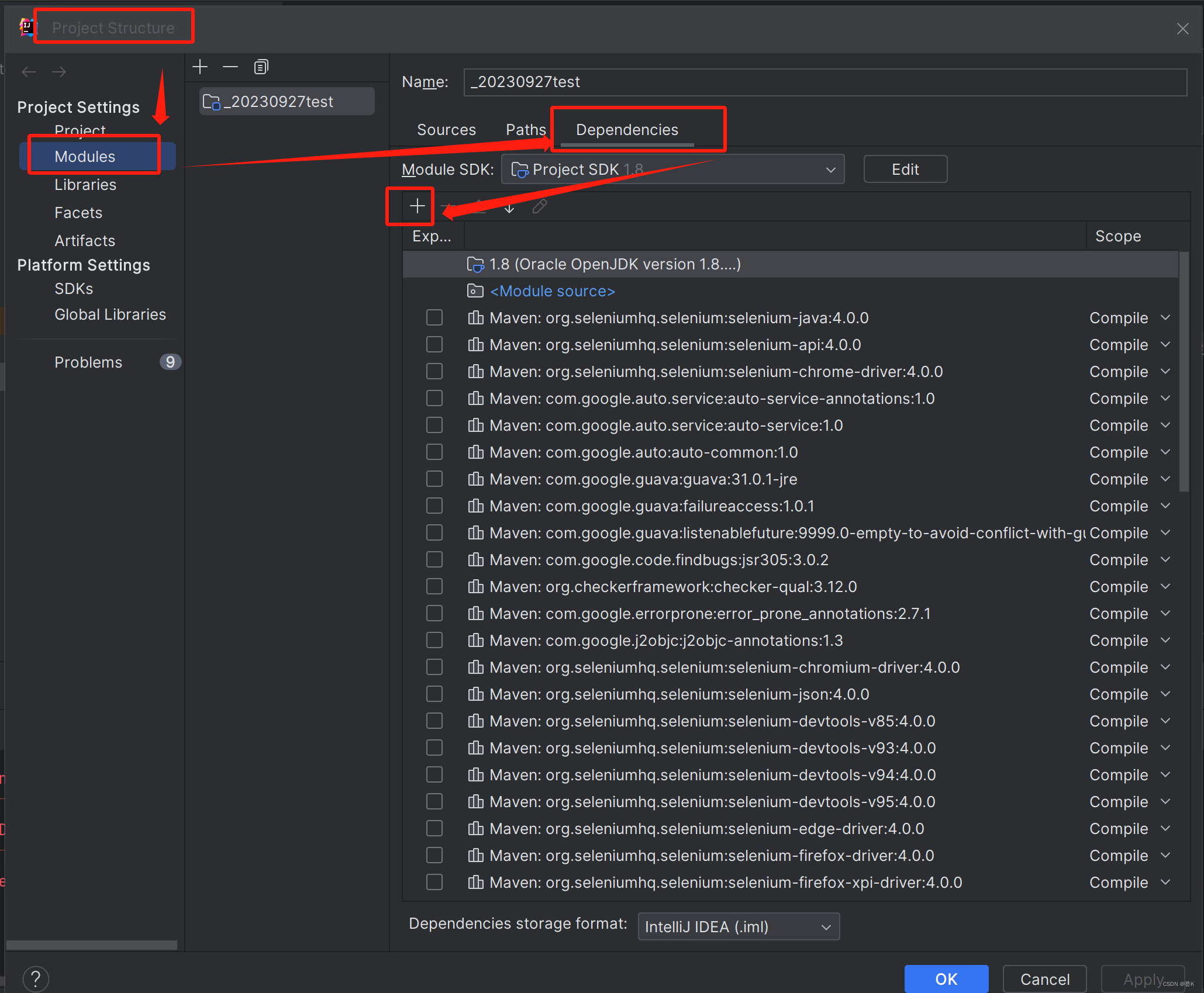
win10搭建Selenium环境+java+IDEA(2)
接着上一个搭建环境开始叙述:win10系统x64安装java环境以及搭建自动化测试环境_荟K的博客-CSDN博客 上一步结尾的浏览器驱动,本人后面改到了谷歌浏览器.exe文件夹下: 这里需要注意,这个新路径要加载到系统环境变量中。 上一步下…...

抢先一步感受未来:Raspberry Pi 5正式发布!
在经历了几年全球供应链困境导致 Raspberry Pi 单板计算机的产能降低和零售价格上涨之后,今天终于迎来了更新。Raspberry Pi 4 上市四年后,今天Raspberry Pi 5正式发布!新推出的 Raspberry Pi 5 配备了经过大幅改进升级的SoC,带来…...

【教程】Ubuntu自动查看有哪些用户名与密码相同的账户,并统一修改密码
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 目录 背景说明 开始操作 修改密码 背景说明 有些用户为了图方便或者初始创建用户默认设置等原因,会将密码设置为与用户名相同,但这就使得非常不安全。甚至如果该用户具有sudo权限&#…...
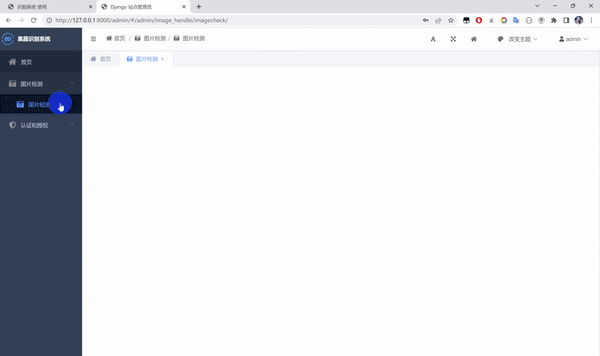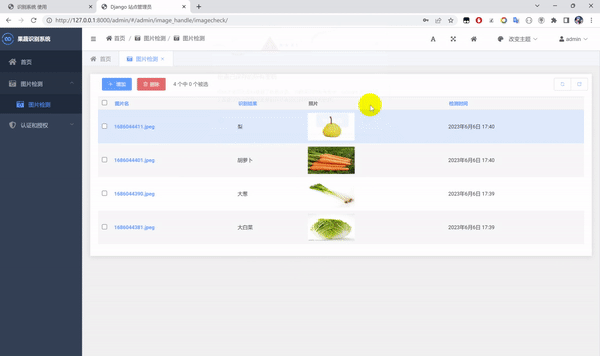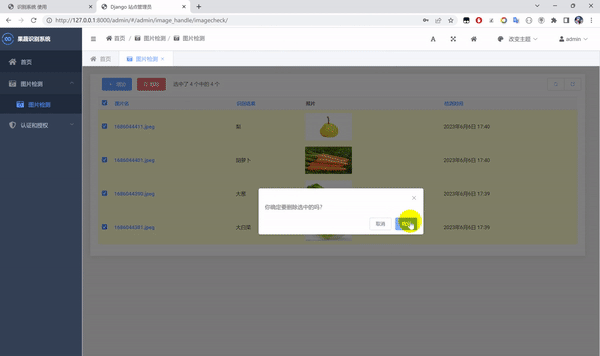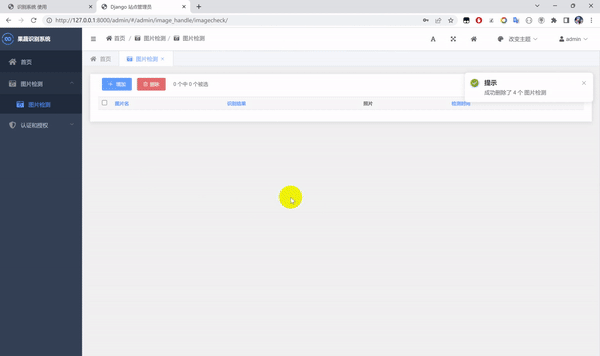
基于 Python+DenseNet121 算法模型实现一个图像分类识别系统
项目展示 一、介绍 DenseNet(Densely Connected Convolutional Networks)是一种卷积神经网络(CNN)架构,2017年由Gao Huang等人提出。该网络的核心思想是密集连接,即每一层都接收其前面所有层的输出作为输…...

贪心算法-点灯问题
1、题目描述 给定一个字符串str,只由 ‘X’ 和 ‘.’ 两种字符构成。‘X’ 表示墙,不能放灯,点亮不点亮都可;’.’ 表示居民点,可以放灯,需要点亮。如果灯放在i位置,可以让 i-1,i 和…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
