最小生成树 | 市政道路拓宽预算的优化 (Minimum Spanning Tree)
任务描述:
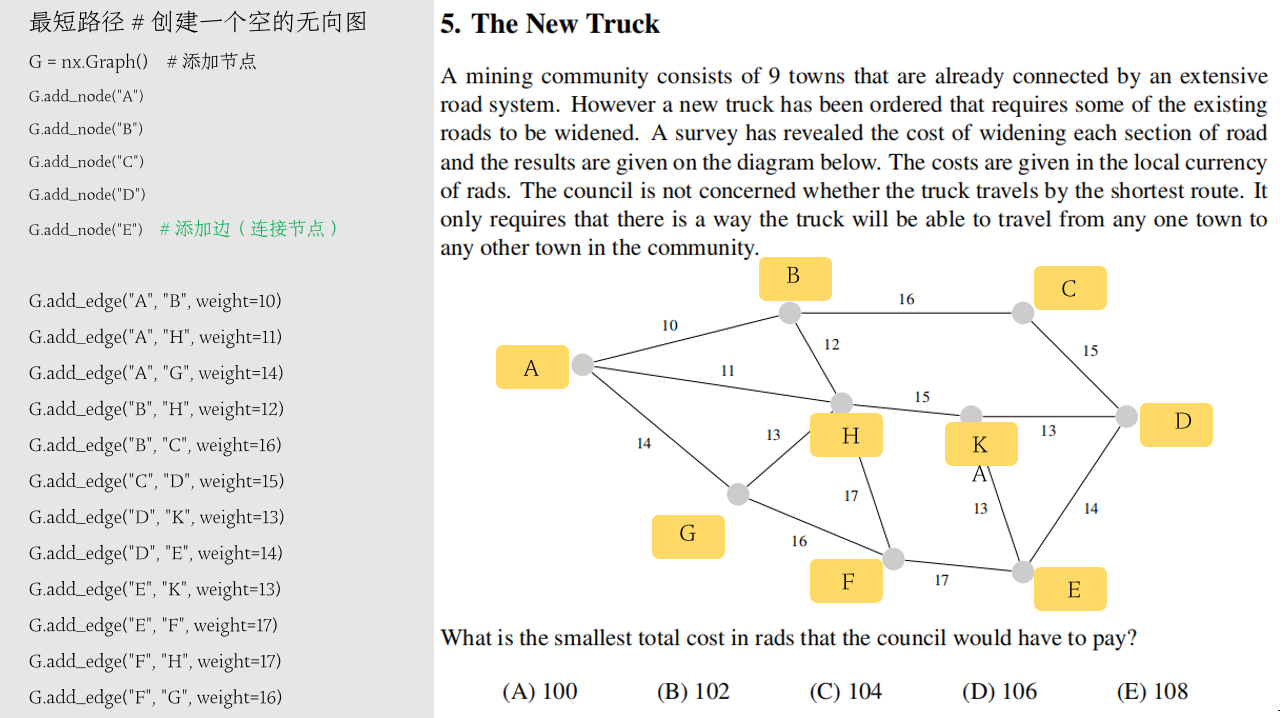
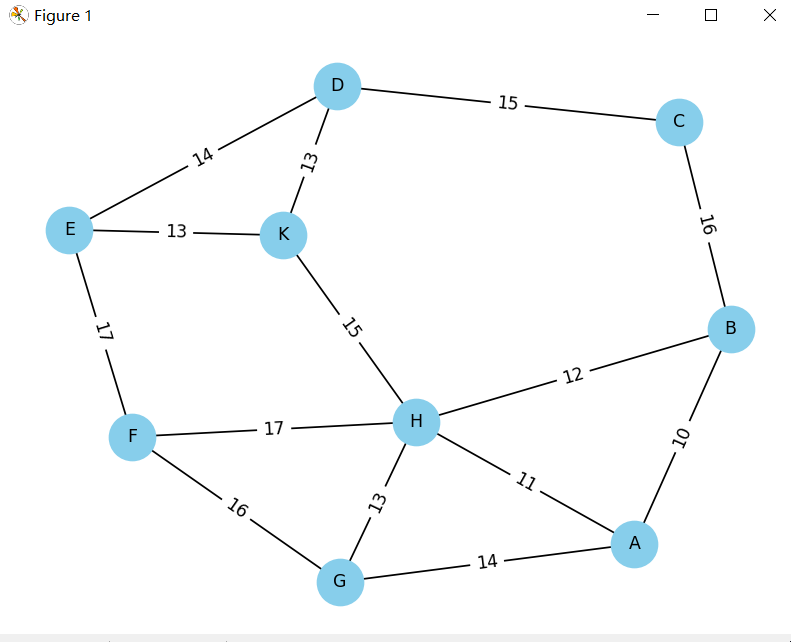
市政投资拓宽市区道路,本着执政为民,节省纳税人钱的目的,论证是否有必要对每一条路都施工拓宽?
这是一个连问带答的好问题。项目制学习可以上下半场,上半场头脑风暴节省投资的所有可行的思路;
下半场总结可行的思路,归为算法问题解决。
思路
MST = Minimum Spanning Tree 最小生成树
1、选择每一个节点的最短边,加入树Tree,涂成颜色标记如下:
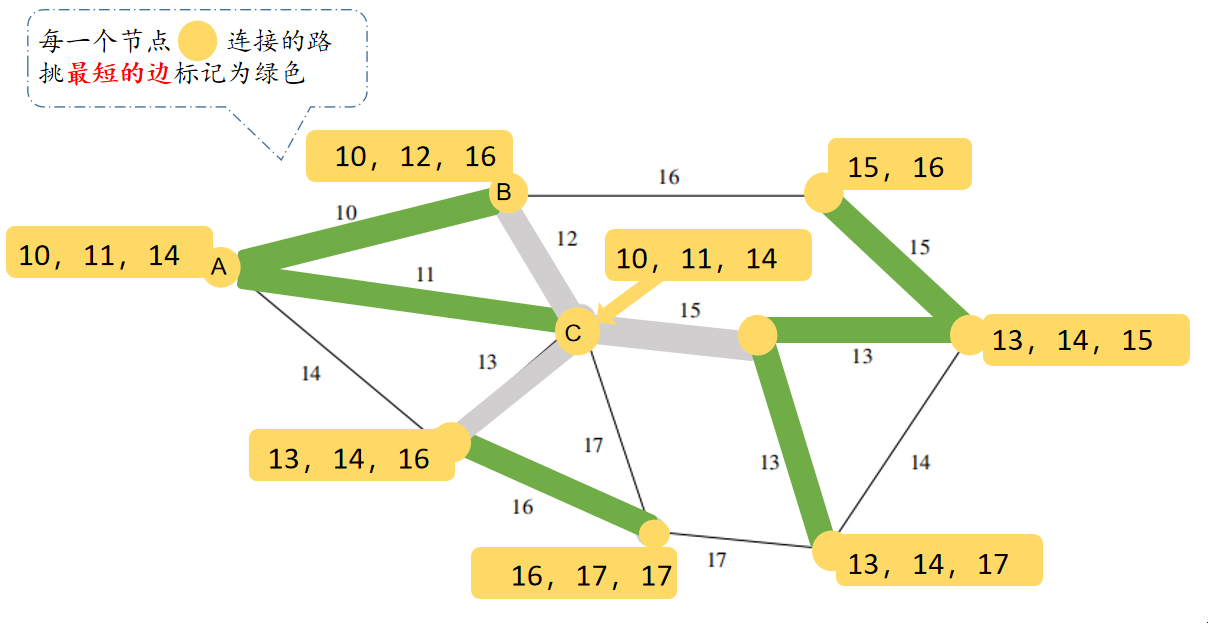
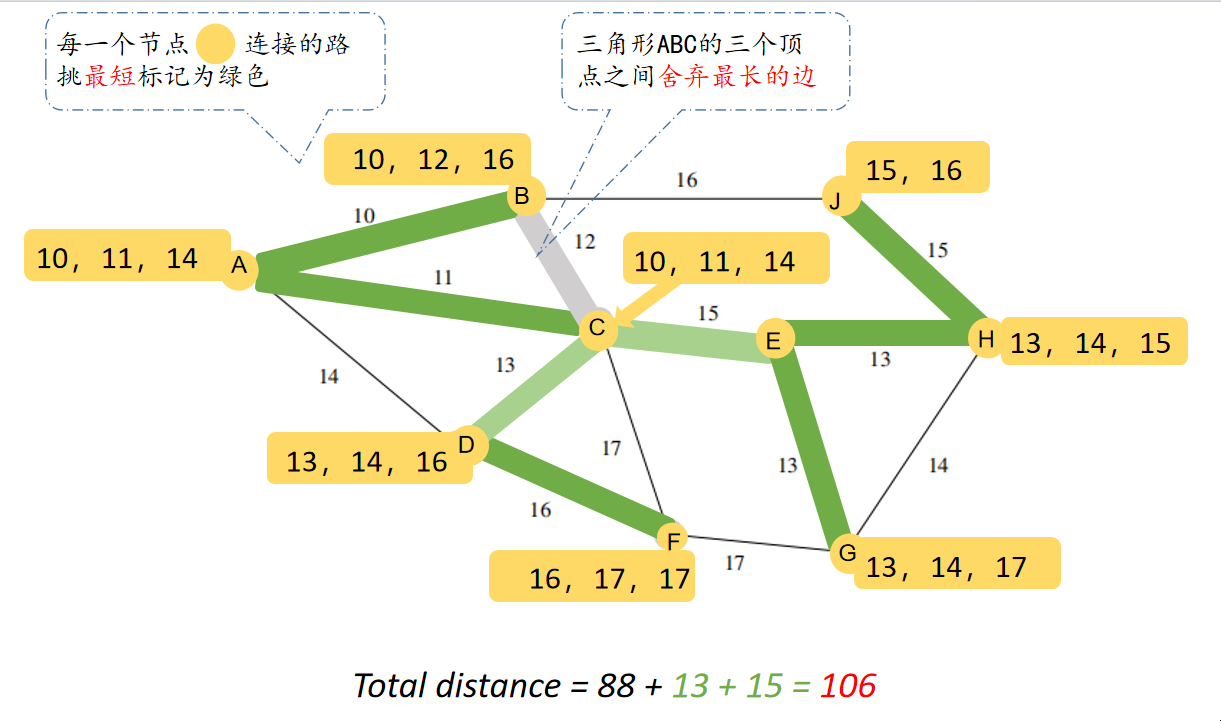
2、同时避免形成环路,

3、遍历所有的节点,循环执行以上步骤直至所有节点都在MST中;
使用Kruskal算法求解最小生成树(Minimum Spanning Tree)的Python代码实现
#上述代码利用Kruskal算法的贪心思想, 每次选择权值最小的边加入MST, 同时避免形成环路,
#直到遍历完所有节点, 得到最小生成树的所有边。
Kruskal算法和Prim算法都是解决最小生成树(Minimum Spanning Tree,MST)问题的常用算法,但它们的工作原理和实现方式略有不同。以下是它们之间的主要区别:
-
工作原理:
-
Kruskal算法:Kruskal算法基于贪心策略。它首先将所有的边按权重升序排列,然后从最小权重的边开始,逐渐构建最小生成树。在构建的过程中,Kruskal算法不断选择下一条最小权重的边,但要确保选择的边不会形成环路。它使用了一个并查集(Disjoint Set)数据结构来判断边是否会形成环路。
-
Prim算法:Prim算法也是一种贪心算法,但它从一个初始顶点开始,逐步添加顶点到最小生成树中。它每次选择一个与当前最小生成树相邻的顶点,并选择连接它们的边中权重最小的那条边。这个过程一直进行,直到所有顶点都包含在最小生成树中为止。
-
-
起始点:
-
Kruskal算法:Kruskal算法不需要指定一个起始点,它从边集合出发,根据权重来构建最小生成树。
-
Prim算法:Prim算法需要指定一个起始点,它从指定的起始点开始构建最小生成树。
-
-
数据结构:
-
Kruskal算法:Kruskal算法主要依赖于边的排序和并查集数据结构,用于检测环路。
-
Prim算法:Prim算法通常使用优先队列(Priority Queue)来管理候选边和顶点,以及一个数组来维护顶点的键(键表示连接到最小生成树的最小边的权重)。
-
-
适用情况:
-
Kruskal算法:Kruskal算法适用于稀疏图,即边相对较少的情况。它不受起始点选择的限制,因此在不同起始点下可能会得到相同的最小生成树。
-
Prim算法:Prim算法适用于稠密图,即边相对较多的情况。它的最终结果可能受起始点选择的影响,因为不同的起始点可能会导致不同的最小生成树。
-
总的来说,Kruskal算法和Prim算法都是有效的最小生成树算法,选择哪个算法取决于具体的问题和图的性质。在实际应用中,可以根据图的密度和其他要求来选择适当的算法。
import sys
class Graph:def __init__(self):self.graph = {}def add_edge(self, u, v, w):if u not in self.graph:self.graph[u] = {}if v not in self.graph:self.graph[v] = {}self.graph[u][v] = wself.graph[v][u] = wdef prim(self):key = {}parent = {}mst_set = set()# 初始化key值为无穷大for vertex in self.graph:key[vertex] = sys.maxsize# 从起始顶点开始start_vertex = list(self.graph.keys())[0]key[start_vertex] = 0parent[start_vertex] = Nonewhile mst_set != set(self.graph.keys()):# 找到key值最小的未加入MST的顶点min_vertex = Nonefor vertex in self.graph:if vertex not in mst_set and (min_vertex is None or key[vertex] < key[min_vertex]):min_vertex = vertexmst_set.add(min_vertex)# 更新与min_vertex相邻的顶点的key值和parentfor neighbor, weight in self.graph[min_vertex].items():if neighbor not in mst_set and weight < key[neighbor]:key[neighbor] = weightparent[neighbor] = min_vertex# 构建最小生成树的边列表mst_edges = []for vertex, p in parent.items():if p is not None:mst_edges.append((p, vertex, key[vertex]))return mst_edges
创建图并添加边
g = Graph()
g.add_edge("A", "B", 10)
g.add_edge("A", "H", 11)
g.add_edge("A", "G", 14)
g.add_edge("B", "H", 12)
g.add_edge("B", "C", 16)
g.add_edge("C", "D", 15)
g.add_edge("D", "K", 13)
g.add_edge("D", "E", 14)
g.add_edge("E", "K", 13)
g.add_edge("E", "F", 17)
g.add_edge("F", "H", 17)
g.add_edge("F", "G", 16)
g.add_edge("G", "H", 13)
g.add_edge("H", "K", 15)
计算最小生成树
mst = g.prim()# 打印最小生成树的边和权重
s = 0
for u, v, w in mst:s += wprint(f"{u} - {v}: {w}")
print('total = ',s)A - B: 10
A - H: 11
H - G: 13
D - C: 15
G - F: 16
H - K: 15
K - D: 13
K - E: 13total = 106
根据图的疏密程度选择合适的最小生成树算法是一个重要的考虑因素。下面是对于不同的图疏密程度如何选择算法的一些建议:
-
稀疏图(Sparse Graph):
-
Kruskal算法:对于稀疏图,通常边的数量相对较少,这使得Kruskal算法的效率较高。因为Kruskal算法不依赖于起始点,适合用于连接各个部分的边比较少的情况。如果图是非连通的,Kruskal算法也可以应对。
-
Prim算法:虽然Prim算法也可以用于稀疏图,但在这种情况下,通常Kruskal算法更具优势,因为它的时间复杂度相对较低。
-
-
稠密图(Dense Graph):
-
Prim算法:稠密图通常包含大量的边,此时Prim算法更适合,因为它在连接到当前最小生成树的顶点之间选择边的效率更高。Prim算法的时间复杂度在稠密图中通常比Kruskal算法更低。
-
-
图的连通性:
-
Kruskal算法:如果图是非连通的,Kruskal算法可以构建最小生成森林,而不需要将图变为连通的。这在一些应用中可能很有用。
-
-
起始点选择:
-
Kruskal算法:Kruskal算法不受起始点选择的限制,因此在不同的起始点下可能会得到相同的最小生成树。这对于某些问题可能是一个优点。
-
Prim算法:Prim算法需要指定一个起始点,因此选择起始点可能会影响最终的最小生成树结果。在某些情况下,选择不同的起始点可能导致不同的最小生成树。
-
总的来说,根据图的疏密程度、连通性和起始点选择的灵活性来选择最小生成树算法。通常,如果图较稀疏,可以优先考虑Kruskal算法,如果图较稠密,可以优先考虑Prim算法。然而,具体的应用可能需要根据问题的特点进行权衡和选择。
同学对算法缺乏兴趣或没有时间研究的,最好的选择,也是Python的优势所在,直接导入第三方库。
额外的福利是收获直观可见的无向图,顺便学习一点可视化。
import networkx as nx
import matplotlib.pyplot as plt#1 创建一个空的无向图
G = nx.Graph()#2 添加节点
G.add_node("A")
G.add_node("B")
G.add_node("C")
G.add_node("D")
G.add_node("E")
G.add_node("F")
G.add_node("G")
G.add_node("H")
G.add_node("K")#根据需求添加边两端连接节点#3 添加边(连接节点)
G.add_edge("A", "B", weight=10)
G.add_edge("A", "H", weight=11)
G.add_edge("A", "G", weight=14)
G.add_edge("B", "H", weight=12)
G.add_edge("B", "C", weight=16)
G.add_edge("C", "D", weight=15)
G.add_edge("D", "K", weight=13)
G.add_edge("D", "E", weight=14)
G.add_edge("E", "K", weight=13)
G.add_edge("E", "F", weight=17)
G.add_edge("F", "H", weight=17)
G.add_edge("F", "G", weight=16)
G.add_edge("G", "H", weight=13)
G.add_edge("H", "K", weight=15)# 绘制图形
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=700, node_color='skyblue', font_size=10, font_color='black')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)# 查找最小生成树
minimum_spanning_tree = nx.minimum_spanning_tree(G)
print("Minimum Spanning Tree Edges:")
s = 0
for edge in minimum_spanning_tree.edges(data=True):s += edge[2]['weight']print(edge)# 查找节点之间的最短路径
shortest_path = nx.shortest_path(G, source="A", target="D", weight="weight")
print("Shortest Path from A to D:", shortest_path)# 计算最短路径长度
shortest_path_length = nx.shortest_path_length(G, source="A", target="D", weight="weight")
print("Shortest Path Length from A to D:", shortest_path_length)# 查找节点之间的最短路径
shortest_path = nx.shortest_path(G, source="H", target="K", weight="weight")
print("Shortest Path from H to K:", shortest_path)# 计算最短路径长度
shortest_path_length = nx.shortest_path_length(G, source="H", target="K", weight="weight")
print("Shortest Path Length from H to K:", shortest_path_length)# Total length of Minimum Spanning Tree Edgesprint(''' totals ''')
print(minimum_spanning_tree) #Graph with 9 nodes and 8 edges
print([edge for edge in minimum_spanning_tree])
print('total length = ',s)# 显示图形
plt.show()
输出结果:
Minimum Spanning Tree Edges:
('A', 'B', {'weight': 10})
('A', 'H', {'weight': 11})
('C', 'D', {'weight': 15})
('D', 'K', {'weight': 13})
('E', 'K', {'weight': 13})
('F', 'G', {'weight': 16})
('G', 'H', {'weight': 13})
('H', 'K', {'weight': 15})Shortest Path from A to D: ['A', 'H', 'K', 'D']
Shortest Path Length from A to D: 39
Shortest Path from H to K: ['H', 'K']
Shortest Path Length from H to K: 15totals
Graph with 9 nodes and 8 edges
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'K']
total length = 106
与原题的图等价。
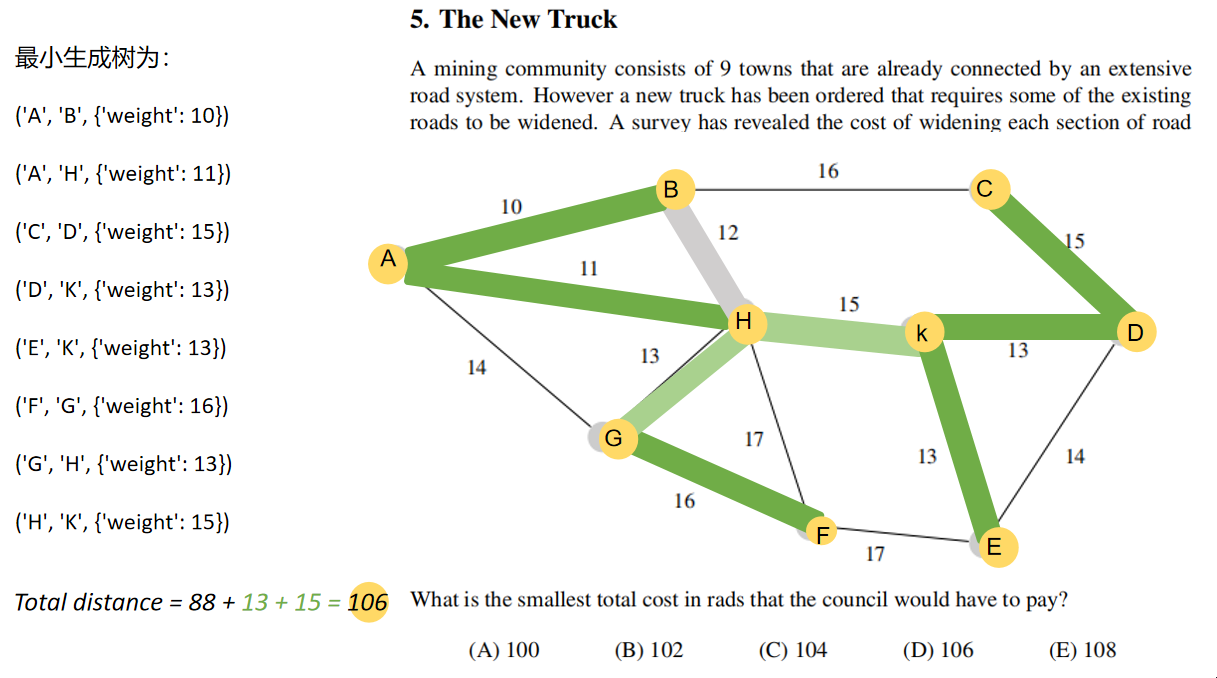
最小生成树为:
('A', 'B', {'weight': 10})
('A', 'H', {'weight': 11})
('C', 'D', {'weight': 15})
('D', 'K', {'weight': 13})
('E', 'K', {'weight': 13})
('F', 'G', {'weight': 16})
('G', 'H', {'weight': 13})
('H', 'K', {'weight': 15})
相关文章:

最小生成树 | 市政道路拓宽预算的优化 (Minimum Spanning Tree)
任务描述: 市政投资拓宽市区道路,本着执政为民,节省纳税人钱的目的,论证是否有必要对每一条路都施工拓宽? 这是一个连问带答的好问题。项目制学习可以上下半场,上半场头脑风暴节省投资的所有可行的思路&a…...
Java实现使用多线程,实现复制文件到另一个目录,起不一样的名字,创建100万个数据
目录 1 需求2 实现 1 需求 我现在有一个300MB 的文件,想要根据这个文件,创建100万个大小一样的,名称不一样,如何实现,如何比较快点实现 2 实现 1 先准备好这个文件 2 准备好目录 3 写代码 private static void crea…...
uni-app:canvas-图形实现1
效果 代码 <template><view><!-- 创建了一个宽度为300像素,高度为200像素的canvas元素。canvas-id属性被设置为"firstCanvas",可以用来在JavaScript中获取该canvas元素的上下文对象。 --><canvas style"width:200p…...
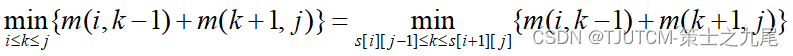
【算法分析与设计】动态规划(下)
目录 一、最长公共子序列1.1 最长公共子序列的结构1.2 子问题的递归结构1.3 计算最优值1.4 举例说明1.5 算法的改进 二、最大子段和2.1 代码2.2 最大子段和问题的分治算法2.3 代码2.4 分治算法的时间复杂度2.5 最大子段和问题的动态规划算法 三、凸多边形最优三角剖分3.1 三角剖…...
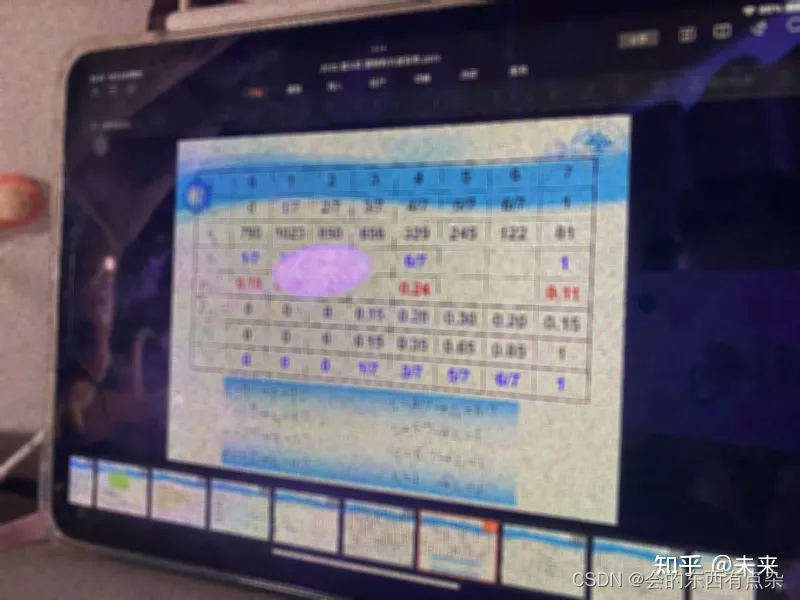
计算机图像处理-均值滤波
均值滤波 线性滤波器的原始数据与滤波结果是一种算术运算,即用加减乘除等运算实现,如均值滤波器(模板内像素灰度值的平均值)、高斯滤波器(高斯加权平均值)等。由于线性滤波器是算术运算,有固定…...
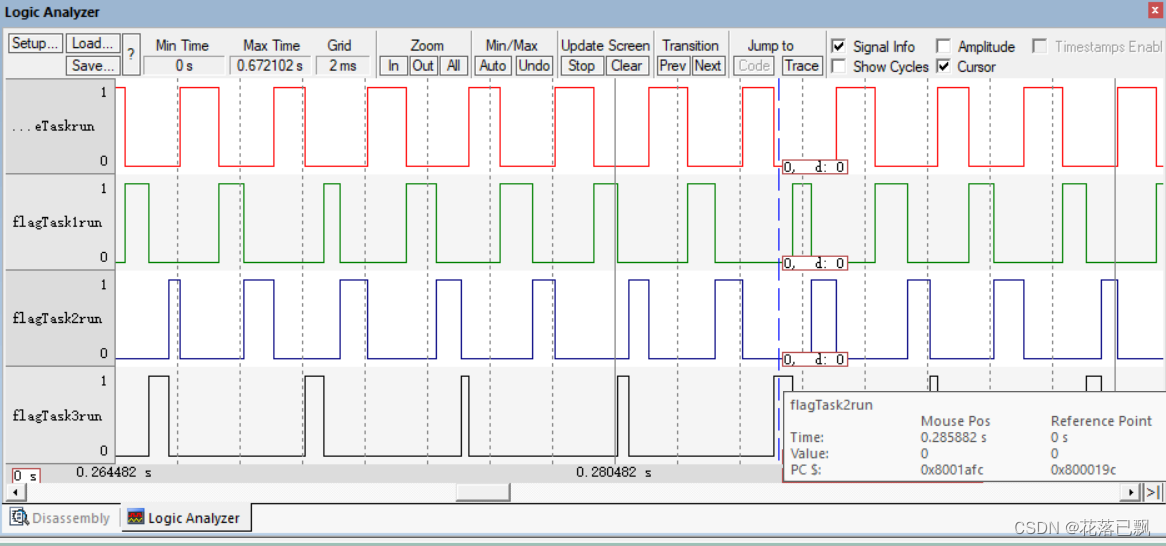
FreeRTOS入门教程(空闲任务和钩子函数及任务调度算法)
文章目录 前言一、空闲任务概念二、钩子函数概念三、任务调度算法四、任务调度算法实验1.实验代码2.是否抢占3.时间片是否轮转4.空闲任务让步 总结 前言 本篇文章将带大家学习一下什么是空闲任务以及钩子函数,以及学习FreeRTOS中的任务调度算法,了解在F…...

Javascript真的是10天内做出来的吗?
我曾听说,Javascript 之所以有这么多缺点,是因为它的第一个版本是在短短十天内完成的。我很好奇:1)这是否属实;2)这是否能解释这种语言的缺陷。 经过一番研究,我可以不自信地说:是的…...

picoctf_2018_got_shell
picoctf_2018_got_shell Arch: i386-32-little RELRO: Partial RELRO Stack: No canary found NX: NX enabled PIE: No PIE (0x8048000)32位,只开了NX int __cdecl __noreturn main(int argc, const char **argv, const char **envp) {_DWOR…...

作用域 CSS 回来了
几年前,消失的作用域 CSS,如今它回来了,而且比以前的版本要好得多。 更好的是,W3C规范基本稳定,现在Chrome中已经有一个工作原型。我们只需要社区稍微关注一下,引诱其他浏览器构建它们的实现,并…...
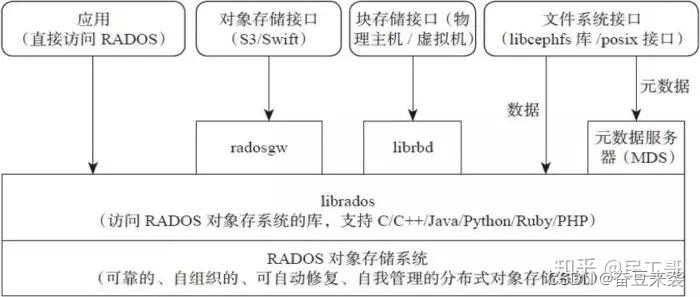
简述ceph文件储存系统
Ceph 是一个统一的分布式存储系统和共享机制,它定义了数据如何存储在一个或多个节点上并呈现给其他机器以供文件访问。 Ceph特点 高性能 a. 摒弃了传统的集中式存储元数据寻址的方案,采用CRUSH算法,数据分布均衡,并行度高。 b.考…...

计算机图像处理:椒盐噪声和高斯噪声
图像滤波 图像滤波,即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,同时会造成图像一定程度上的模糊,这也叫做平滑或者低通滤波。无论是均衡化直方图和图像滤波,都一定程度上降低了图像阈值分割的难度,直…...

SQL SELECT 子查询与正则表达式
在之前的文章中已经探讨了 SQL SELECT 语句的基础和进阶用法,以及如何通过高级技巧来进行更复杂的数据查询和分析。本文将介绍 SQL SELECT 语句中的子查询和正则表达式的使用。这些是 SQL 中非常强大的工具,能让您进行更复杂和精细的数据操作。 文章目录 子查询基础与应用子…...

Package vips was not found in the pkg-config search path的解决方案
出现该问题是因为pkg-config未安装或未成功设置环境变量。 下文是centos下的操作。 前提 先安装C编译环境: yum -y install gcc-c 否则会报错configure: error: no acceptable C compiler found in $PATH 成功后gcc -v会显示版本信息。 下载&安装 pkg-config 传…...
Vue封装全局SVG组件
1.SVG图标配置 1.安装插件 npm install vite-plugin-svg-icons -D 2.Vite.config.ts中配置 import { createSvgIconsPlugin } from vite-plugin-svg-icons import path from path export default () > {return {plugins: [createSvgIconsPlugin({// Specify the icon fo…...
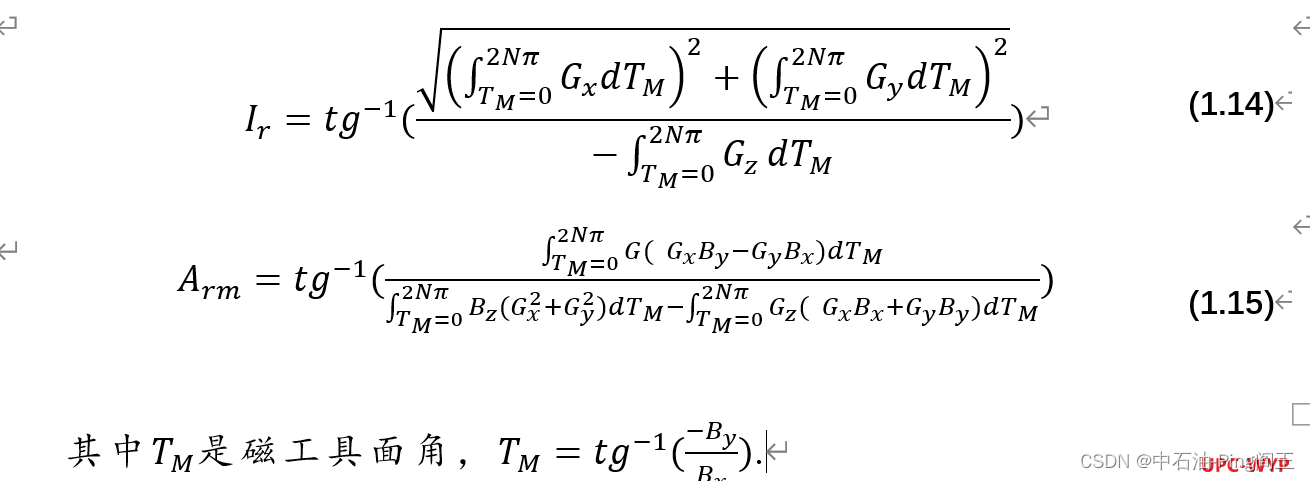
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
磁性测量工具安装在非磁性钻铤内,如图1,以避免磁性随钻测量工具测量时受到外部干扰。 测量系统采用三轴加速度计和三轴磁通门,并采用冗余设计,由于井下振动剧烈,陀螺仪的可靠性将大大降低。为了保证整个钻井过程中系统…...
Docker-Windows安装使用
1.下载docker https://cr.console.aliyun.com/cn-hangzhou/instances/mirrors 2.配置虚拟化环境 通过控制面板“设置”启用 Hyper-V 角色 右键单击 Windows 按钮并选择“应用和功能”。选择相关设置下右侧的“程序和功能”。选择“打开或关闭 Windows 功能”。选择“Hyper-…...

在Windows11上安装ubuntu虚拟机
一开始是参考了 VMware17虚拟机安装Ubuntu最新版本(Ubuntu22.04LTS)详细步骤 专栏的1和2来的。但是后面总是提示operating system not found,就参考vmware安装ubuntu时总是提示operating system not found,选择典型安装而不是专栏选择的自定义安装&#…...

【微服务】spring 控制bean加载顺序使用详解
目录 一、前言 二、使用order注解控制顺序 2.1 order 注解使用示例 2.2 order注解顺序失效问题 2.2.1 order失效问题解决办法 2.3 实现Ordered接口 三、使用dependon注解控制顺序 四、AutoConfiguration注解控制bean加载顺序 4.1 AutoConfigureBefore 操作演示 4.2 A…...
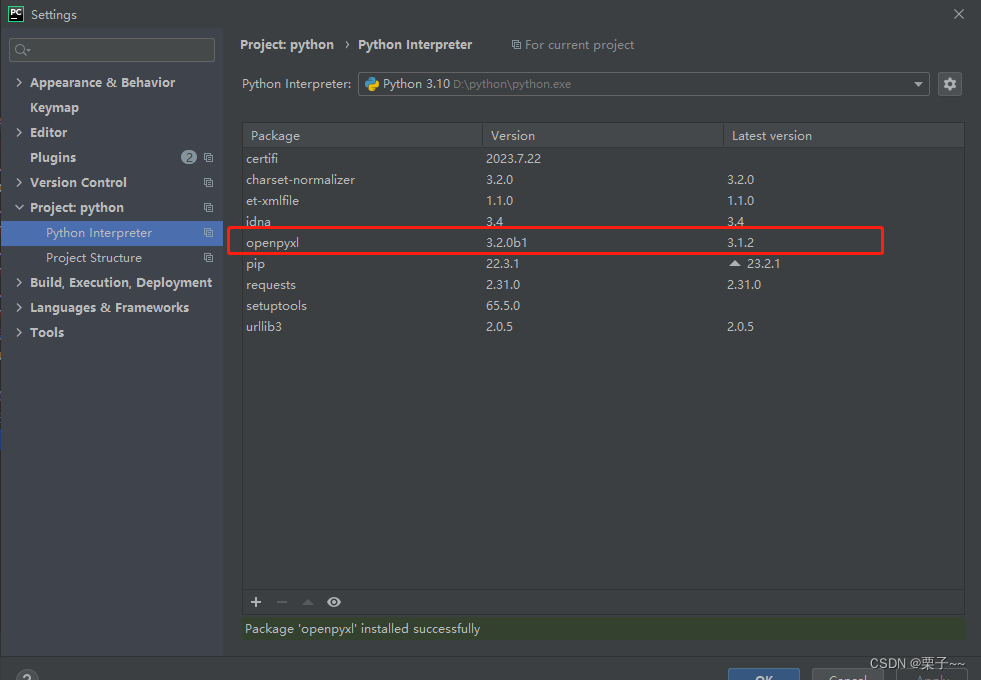
python-切换镜像源和使用PyCharm进行第三方开源包安装
文章目录 前言python-切换镜像源和使用PyCharm进行第三方开源包安装1. 切换镜像源2. 使用PyCharm进行第三方开源包安装 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每…...
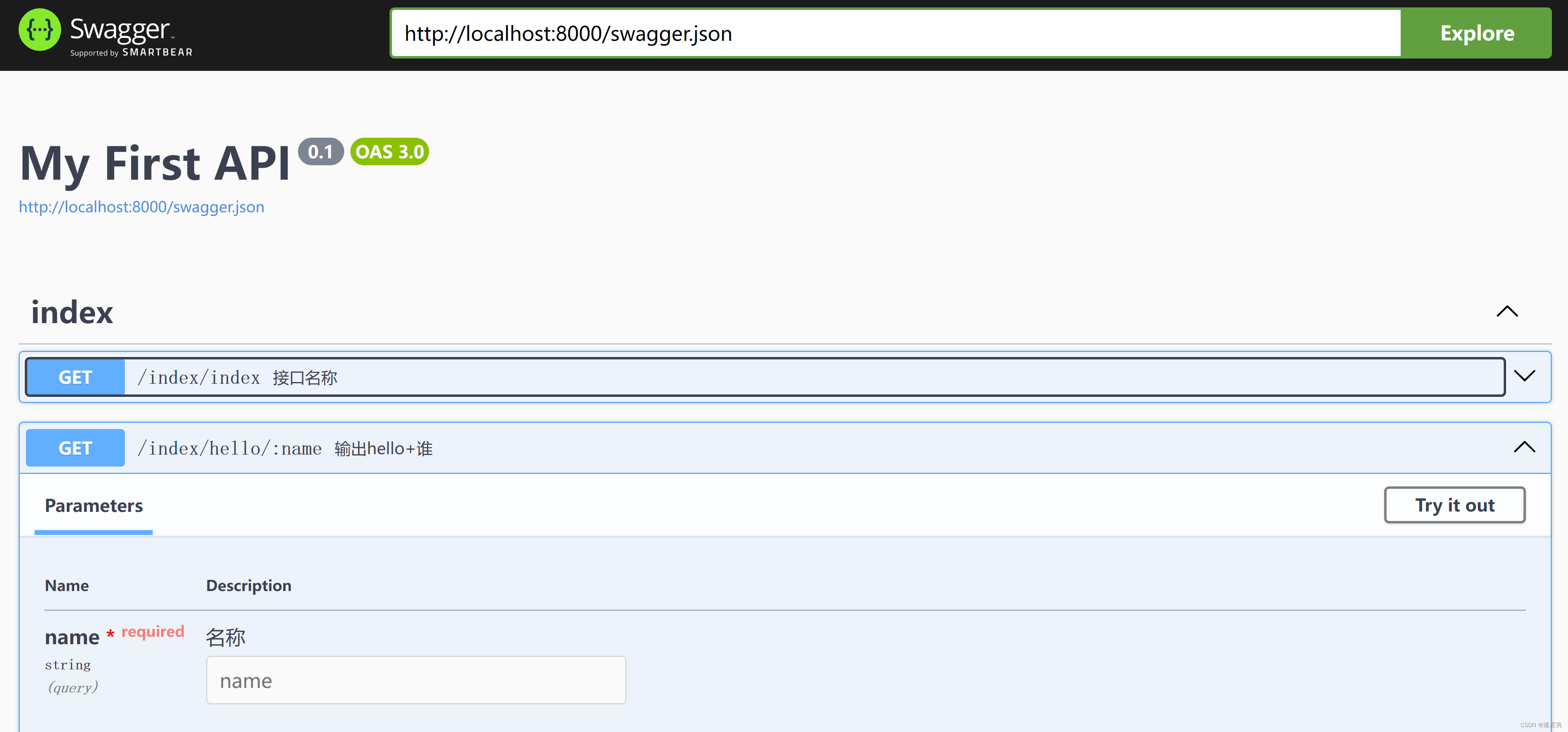
tp6 + swagger 配置文档接口
ThinkPHP 6.0 运行环境要求PHP7.2,兼容PHP8.1 安装 composer create-project topthink/think tp 6.0.*如果需要更新框架使用 composer update topthink/framework文档 完全开发手册 swagger 文档 注解文档 安装包 composer require zircote/swagger-php 引用…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
