机器人中的数值优化|【五】BFGS算法非凸/非光滑处理
机器人中的数值优化|【五】BFGS算法的非凸/非光滑处理
往期内容回顾
机器人中的数值优化|【一】数值优化基础
机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例
机器人中的数值优化|【三】无约束优化,拟牛顿法理论与推导
机器人中的数值优化|【四】L-BFGS理论推导与延伸
在往期中我们对拟牛顿法以及BFGS等算法进行了详细的推导和学习,但是之前讨论的都为在保证函数凸且光滑的情况,那么如果函数非凸或者非光滑呢?我们在本节中进行一下研究。
非光滑的函数BFGS优化算法
Weak Wolfe Condition
sufficient decrease condition:
S ( α ) : f ( x k ) − f ( x k + α d ) ≥ − c 1 α d T ∇ f ( x k ) S(\alpha):f(x^k)-f(x^k+\alpha d)\ge-c_1 \alpha d^T\nabla f(x^k) S(α):f(xk)−f(xk+αd)≥−c1αdT∇f(xk)
curvature condition:
C ( α ) : d T ∇ f ( x k + α d ) ≥ c 2 d T ∇ f ( x k ) C(\alpha):d^T\nabla f(x^k+\alpha d)\ge c_2 d^T \nabla f(x^k) C(α):dT∇f(xk+αd)≥c2dT∇f(xk)
Lewis & Overton line search:
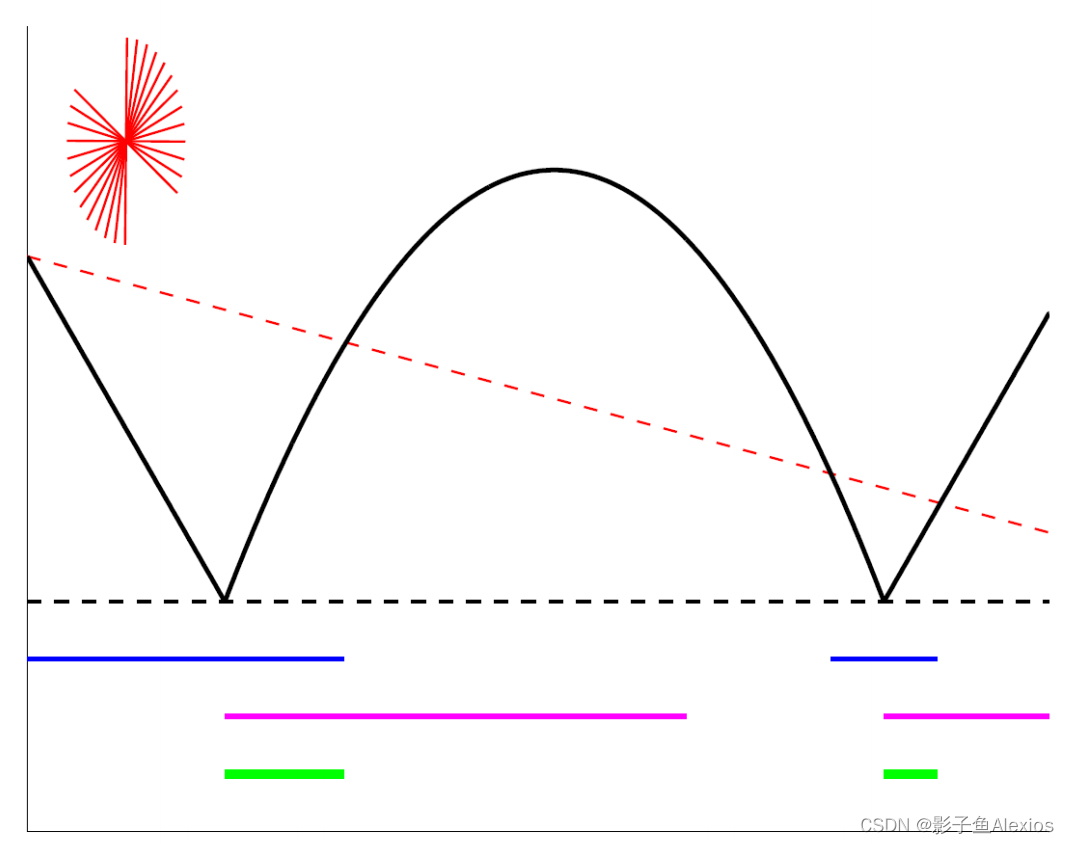
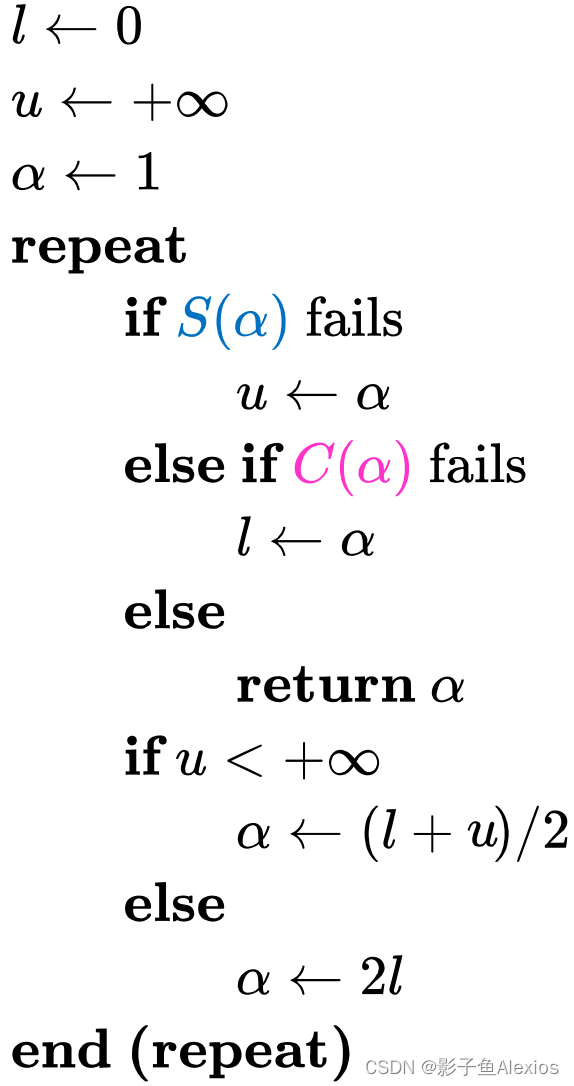
非凸但平滑的函数BFGS优化算法
Cautious-Limited-Memory-BFGS
非凸非平滑函数的BFGS优化算法

相关文章:

机器人中的数值优化|【五】BFGS算法非凸/非光滑处理
机器人中的数值优化|【五】BFGS算法的非凸/非光滑处理 往期内容回顾 机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例 机器人中的数值优化|【三】无约束优化࿰…...
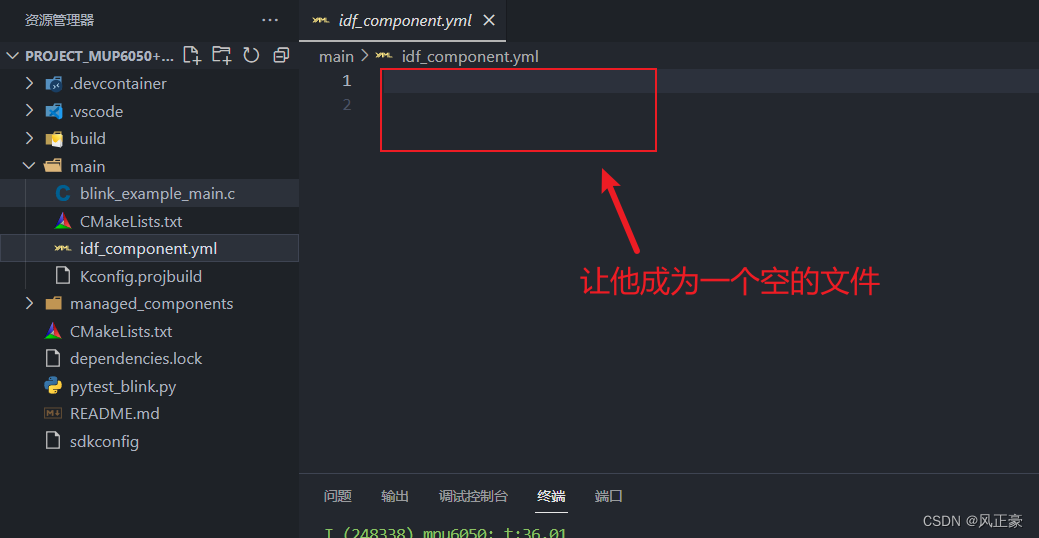
ESP32S3的MPU-6050组件移植教程
前言 (1)实习公司要搞ESP32BOX的驱动移植,所有资料自己找还是比较折磨人的现在我分享几个官方的组件移植资料: <1>Find the most exciting ESP-IDF components(ESP32的官方组件都可以在里面查,按照他…...
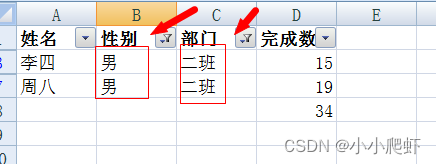
excel筛选后求和
需要对excel先筛选,后对“完成数量”进行求和。初始表格如下: 一、选中表内任意单元格,按ctrlshiftL,开启筛选 二、根据“部门”筛选,比如选择“一班” 筛选完毕后,选中上图单元格,然后按alt后&…...

pyspark 检测任务输出目录是否空,避免读取报错
前言 在跑调度任务时候,有时候子任务需要依赖前置任务的输出,但类似读取 Parquet 或者 Orc 文件时,如果不判断目录是否为空,在输出为空时会报错,所以需要 check 一下,此外Hadoop通常在写入数据时会在目录中…...

「网页开发|前端开发|Vue」10 vuex模块化:将数据划分成不同modules分别管理
本文主要介绍如何使用vuex的modules将状态数据根据不同模块进行划分并分别管理以及如何使用mapGetters快速将状态管理中的数据导入成local变量。 文章目录 本系列前文传送门一、场景说明二、使用modules划分不同模块三、使用Getters获取状态管理数据Getter传参mapGetters 辅助…...

苹果CMS插件-苹果CMS全套插件免费
网站内容的生成和管理对于网站所有者和内容创作者来说是一个挑战。有一些强大的工具可以帮助您轻松地解决这些问题。苹果CMS插件自动采集插件、采集发布插件以及采集伪原创发布插件,是这些工具之一。它们不仅可以极大地节省您的时间和精力,还可以提高您网…...

域环境介绍
一、概述 内网也指局域网,指的是某个区域由多台计算机互连而成的计算机组,范围通常在数千米以内,在局域网中,可以实现文件管理,应用软件共享,打印机共享、工作组内的日程安排、电子邮件和传真通信服务等&a…...

地球同步静止轨道上的中国卫星
3万6千公里地球同步静止轨道上的中国控制的卫星(包括香港属非国产平台卫星、外国属中国平台卫星),共80颗;截止到2023年8月3日,共有563颗在轨卫星。 号定位名称发射时间用途重量1141.1W中星1C(FH2C)2015.12.10DFH4平台…...
)
HAProxy代理TCP(使用HAProxy 为TiDB-Server 做负载均衡)
目录 一、使用HAProxy 为TiDB-Server 做负载均衡环境1、创建文件夹2、配置haproxy.cfg3、创建 docker-compose.yaml 文件haproxy.cfg 配置说明[参照官方文档](https://pingcap.com/docs-cn/v3.0/reference/best-practices/haproxy/ "参照官方文档") 一、使用HAProxy …...

全新自适应导航网模板 导航网系统源码 网址导航系统源码 网址目录网系统源码
高价值目录网导航网整站源码 | 2999元价值,最新版本源码下载推荐 1、导航网一键获取目标站SEO信息,7.5版本增加会员中心一键获取网站信息网站权重,增加小程序提交发布,全新自适应模板; 2、可设置游客提交、游客提交人工审核,会员免审提交,会员提交人工审核,VIP会员免…...

无人直播间
失败!! 采用 ffmpeg 技术进行推流 推流代码: 【需要将rtmp替换为你的推流地址】 ffmpeg -re -stream_loop -1 -i "rain.mp4" -c copy -f flv ""推流地址获取 以哔哩哔哩为例 点击下方链接 开播设置 - 个人中心 - …...

Linux 服务器防止 ssh 暴力密码登录破解之使用 fail2ban
前言,网络安全越来越重要,如何保证网站安全至关重要,在使用 Linux 服务器时,如果未设置有效安全登录屏障,每日将会有数百甚至数万次的密码暴力尝试登录,本篇章将介绍两种 Linux 登录安全防护 一࿱…...

第十四届蓝桥杯大赛软件赛决赛 C/C++ 大学 B 组 试题 D: 合并数列
[蓝桥杯 2023 国 B] 合并数列 【问题描述】 小明发现有很多方案可以把一个很大的正整数拆成若干正整数的和。他采取了其中两种方案,分别将他们列为两个数组 { a 1 , a 2 , ⋯ a n } \{a_1, a_2, \cdots a_n\} {a1,a2,⋯an} 和 { b 1 , b 2 , ⋯ b m } \{b…...
ChatGPT必应联网功能正式上线
今日凌晨发现,ChatGPT又支持必应联网了!虽然有人使用过newbing这个阉割版的联网GPT4,但官方版本确实更加便捷好用啊! 尽管 ChatGPT 此前已经展现出了其他人工智能模型无可比拟的智能,但由于其训练数据的限制ÿ…...
)
DETR中的问题汇总(代码)
一、讲述一下torch.tensor()和torch.as_tensor()的区别 torch.tensor() 和 torch.as_tensor() 都是 PyTorch 中用于创建张量(Tensor)的函数,但它们有一些区别,主要涉及到张量的内存管理方式和数据拷贝。以下是它们的主要区别&…...

华为云云耀云服务器L实例评测|使用华为云耀云服务器L实例的CentOS部署Docker并运行Tomcat应用
目录 前言 步骤1:登录到华为云耀云服务器L实例 步骤2:安装Docker 并验证Docker安装 步骤3:拉取Tomcat镜像并运行Tomcat容器 步骤4:放行8080端口 步骤5:访问tomcat 步骤6:管理Tomcat容器 小结 前言 …...

Java基础---第八篇
系列文章目录 文章目录 系列文章目录一、a=a+b与a+=b有什么区别吗?二、try catch finally,try里有return,finally还执行么?三、Excption与Error包结构一、a=a+b与a+=b有什么区别吗? += 操作符会进行隐式自动类型转换,此处a+=b隐式的将加操作的结果类型强制转换为持有结果…...
(附源码)springboot体检预约APP 计算机毕设16370
目 录 摘要 1 绪论 1.1开发背景 1.2研究现状 1.3springboot框架介绍 1.4论文结构与章节安排 2 Springboot体检预约APP系统分析 2.1 可行性分析 2.1.1 技术可行性分析 2.1.2 经济可行性分析 2.1.3 操作可行性分析 2.2 系统流程分析 2.2.1 数据添加流程 2.2.2 数据…...

Spring的注解开发-@Component的三个衍生注解
由于JavaEE开发是分层的(三层架构体系,控制层、服务层、持久层),为了每层Bean标识的注解语义化更加明确,Component又衍生出以下三个注解 注解用途Repository(仓库)标识持久层(DAO&am…...

无线WIFI工业路由器可用于楼宇自动化
钡铼4G工业路由器支持BACnet MS/TP协议。BACnet MS/TP协议是一种用于工业自动化的开放式通信协议,被广泛应用于楼宇自动化、照明控制、能源管理等领域。通过钡铼4G工业路由器的支持,可以使设备间实现高速、可靠的数据传输,提高自动化水平。 钡…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
