时间和空间复杂度
文章目录
前言
一、算法效率
1.如何评判算法效率?
2.算法的复杂度
二、时间复杂度
1.时间复杂度的定义
2. 大O的渐进表示法
三、空间复杂度
总结
前言
本文章讲解时间与空间复杂度
提示:以下是本篇文章正文内容,下面案例可供参考
一、算法效率
1.如何评判算法效率?
如果我们按照计算机的性能来作为算法的效率
会出现什么样的结果呢?
举个例子:
我们用当年美国登月的计算机CPU
与现在的i9-13900CPU来跑以下代码:
谁更快呢?
long long Fib(int N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
根本不需要质疑一定是现在的CPU
2.算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
二、时间复杂度
1.时间复杂度的定义
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}Func1 执行的基本操作次数 :
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这
里我们使用大O的渐进表示法。
2. 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
三、空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
四、复杂度对比图
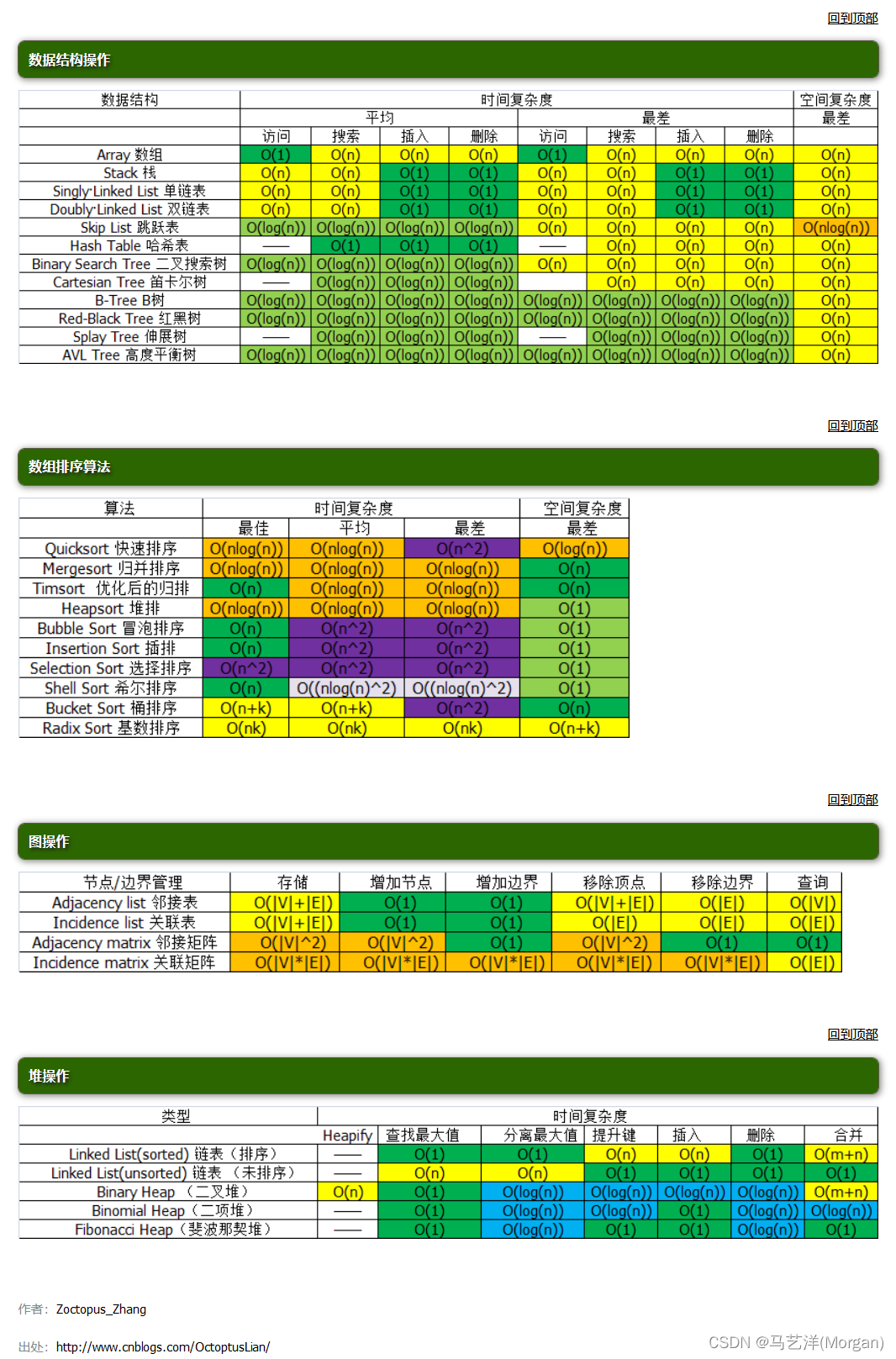
总结
算法时间和空间复杂度的介绍与认识,使用方法
相关文章:

时间和空间复杂度
文章目录 前言 一、算法效率 1.如何评判算法效率? 2.算法的复杂度 二、时间复杂度 1.时间复杂度的定义 2. 大O的渐进表示法 三、空间复杂度 总结 前言 本文章讲解时间与空间复杂度 提示:以下是本篇文章正文内容,下面案例可供参考 一、算法…...

关于Linux下调试
关于Linux下调试 无论是内核(操作系统)还是应用程序,都存在需要调试的情况。 所谓工欲善其事,必先利其器。一个好的称手的工具,对于快速分析问题、定位问题,提高效率,非常有帮助。 除了工具&a…...

理解TP、FP、TN、FN
概念定义 按照常用的术语,将两个类分别称为正类 (positive) 和 负类 (negative)。使用数学表示: 1表示正类 , -1 表示负类。 正类通常是少数类,即样本较少的类(例如有缺陷的零件) 负类通常是多数类&#x…...
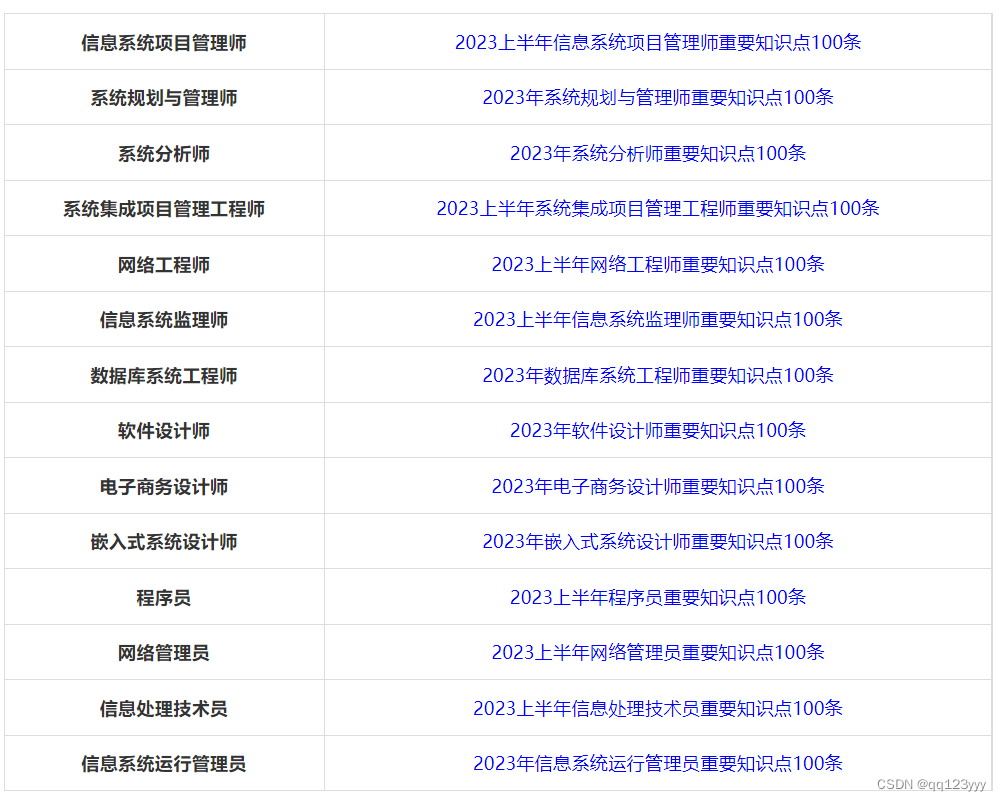
软考中级有用吗
当然有用了! 软考“简历”:计算机软件资格考试在全国范围内已经实施了二十多年,近十年来,考试规模持续增长,截止目前,累计报考人数约有五百万人。该考试由于其权威性和严肃性,得到了社会各界及用人单位的广泛认同&…...

计算机网络之IP协议(详解
网络层主管地址管理与路由选择。而IP协议就是网络层中一个非常重要的协议。它的作用就是在复杂的网络环境中确定一个合适的路径。IP协议头格式4位版本号(version) 指定IP协议的版本,目前只有两个版本:IP v4和IP v6.对于IP v4来说,这个值就是4…...

Kubernetes之探针probe
deployment只保证pod的状态为running。如果pod状态是running,但是里面丢失了文件,导致用户不能访问数据,则deployment是不管用的,此时就需要probe来检测pod是否正常工作。 probe是定义在容器里的,可以理解为容器里加的…...
高性能低功耗4口高速USB2.0 HUB NS1.1S 兼容FE1.1
NS1.1S是一款高性能、低功耗4口高速 USB2.0 HUB 控制器,上行端口兼容高速 480MHz和全速12MHz两种模式,4个下行端口兼容高速480MHz、全速12MHz、低速1.5MHz三种模式。 NS1.1S采用状态机单事务处理架构,而非单片机架构,多个事务缓冲…...

通过VS Code轻松连接树莓派
如果您正在使用树莓派作为开发平台,那么通过远程连接VS Code到树莓派是非常方便的一种方法。这样,您可以在Windows或macOS等计算机上开发和测试代码,而不必在树莓派上进行。 以下是通过VS Code远程连接到树莓派的步骤: 1.安装Re…...

图纸等敏感文件数据外发时 如何确保效率和安全性?
很多企业随着业务的发展,需要频繁的与外部供应商、合作伙伴之间进行数据的交换和使用。尤其是制造型企业,可能每天都要与几十、上百家供应商及合作伙伴进行产品数据交换。目前,大多数企业已经在内部实施了PDM/PLM系统,实现了对组织…...
)
2023年CDGA考试-第4章-数据架构(含答案)
2023年CDGA考试-第4章-数据架构(含答案) 单选题 1.请从下列选项中选择不属于数据架构师职责的选项 A.确保数据架构和企业战略及业务架构一致 B.提供数据和组件的标准业务词汇 C.设计企业数据模型 D.整合企业数据架构蓝图 答案 C 2.请从下列选项中选择不属于企业数据架构…...
理解随机游走
随机游走 基本思想 从一个或一系列顶点开始遍历一张图。在任意一个顶点,遍历者将以概率1-a游走到这个顶点的邻居顶点,以概率a随机跳跃到图中的任何一个顶点,称a为跳转发生概率,每次游走后得出一个概率分布,该概率分布…...

mqtt协议1- 简介和报文格式
文章目录1.mqtt协议1: 简介和报文格式1.1.MQTT概念1.2.数据2.控制报文格式2.1.MQTT数据包结构2.2.固定头2.2.1.控制报文类型2.2.2.标志FLag2.2.3.剩余长度2.3.可变头2.4.有效载荷Payload消息体安全QoS(Quality of Service levels)ref:1.mqtt协议1: 简介和报文格式 Message Que…...

前端用动画快速实现骨架屏效果
一、动画的语法 1.定义动画 keyframes 自定义动画名称 {// 开始from {transform: scale(1);}// 结束to {transform: scale(1.5);} }// 或者还可以使用百分比定义keyframes 动画名称 {// 开始0% {transform: scale(1);}// 结束100% {transform: scale(1.5);} } 2.调用 anima…...

Python入门(未完待续。。。)
认识python 解释型(写完直接运行)、面向对象的高级编程语言;开源免费、支持交互式、可跨平台移植的脚本语言;优点:开源、易于维护、可移植、简单优雅、功能强大、可扩展、可移植;缺点:解释型→运…...

注解配置SpringMVC
使用配置类和注解代替web.xml和Spring和SpringMVC配置文件的功能。创建初始化类,代替web.xmlSpring3.2引入了一个便利的WebApplicationInitializer基础实现,名为AbstractAnnotationConfigDispatcherServletInitializer,当我们的类扩展了Abstr…...

多项新规重磅发布,微信视频号近期需要关注这几点
随着功能的完善和内容生态的丰富,视频号逐渐放慢产品更新频率,将重点放到商家准入标准、创作者扶持计划上来,本期我们将更侧重解读平台新规,帮助大家了解行业动向,把握最新趋势。01 视频号小店结算规则修订 取消48小时…...

Java调用第三方http接口的方式
1. 概述 在实际开发过程中,我们经常需要调用对方提供的接口或测试自己写的接口是否合适。很多项目都会封装规定好本身项目的接口规范,所以大多数需要去调用对方提供的接口或第三方接口(短信、天气等)。 在Java项目中调用第三方接…...

【跟我一起读《视觉惯性SLAM理论与源码解析》】第五章第六章 对极几何图优化库的使用
极平面,极点,极线的概念对极几何,对极约束的概念,通过叉积以及点积的性质推导单应矩阵以及基础矩阵光束平差法BA是LSAM中常用的非线性优化方法一个图由若干个顶点以及这些顶点连接的边构成,顶点通常是待优化的变量例如…...
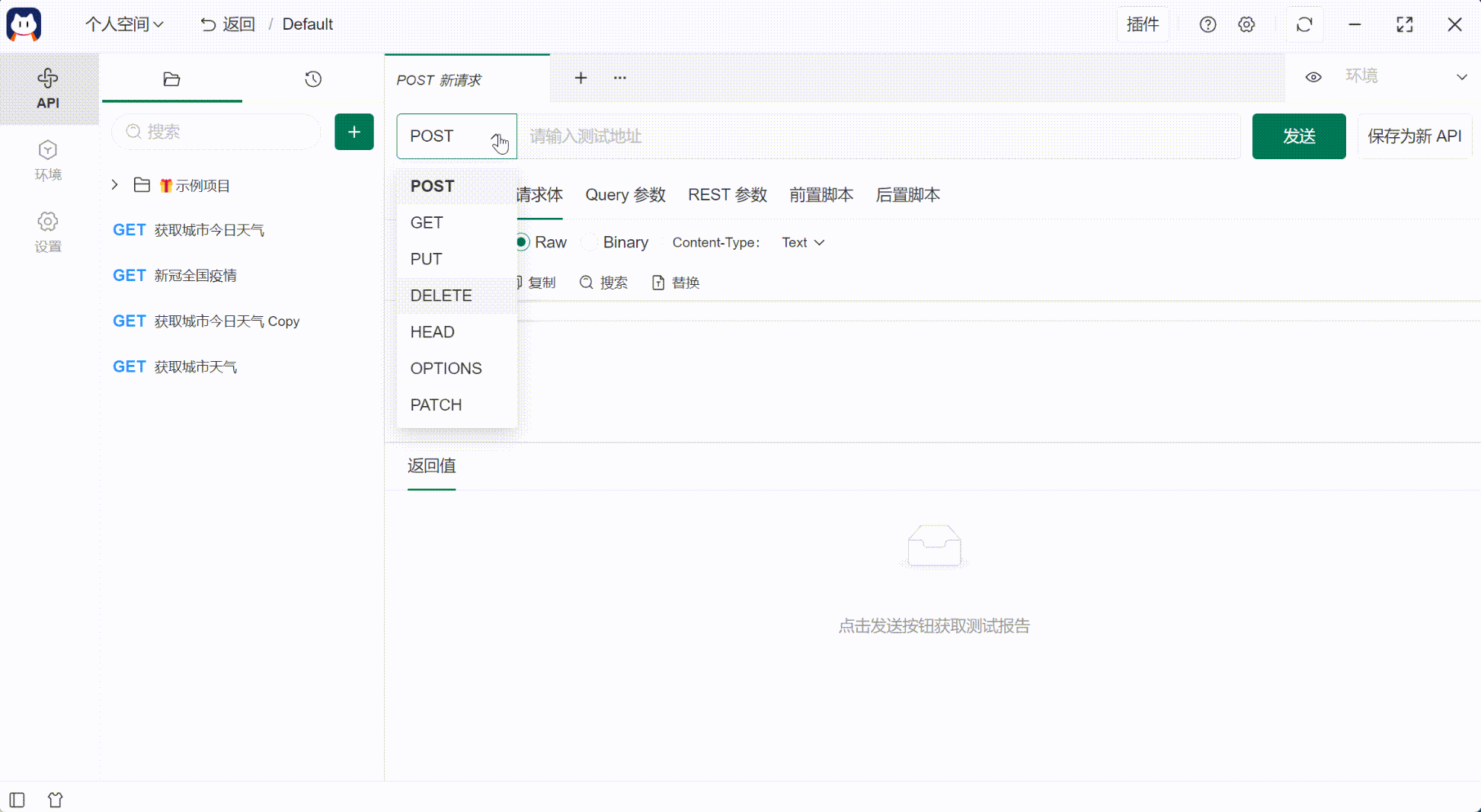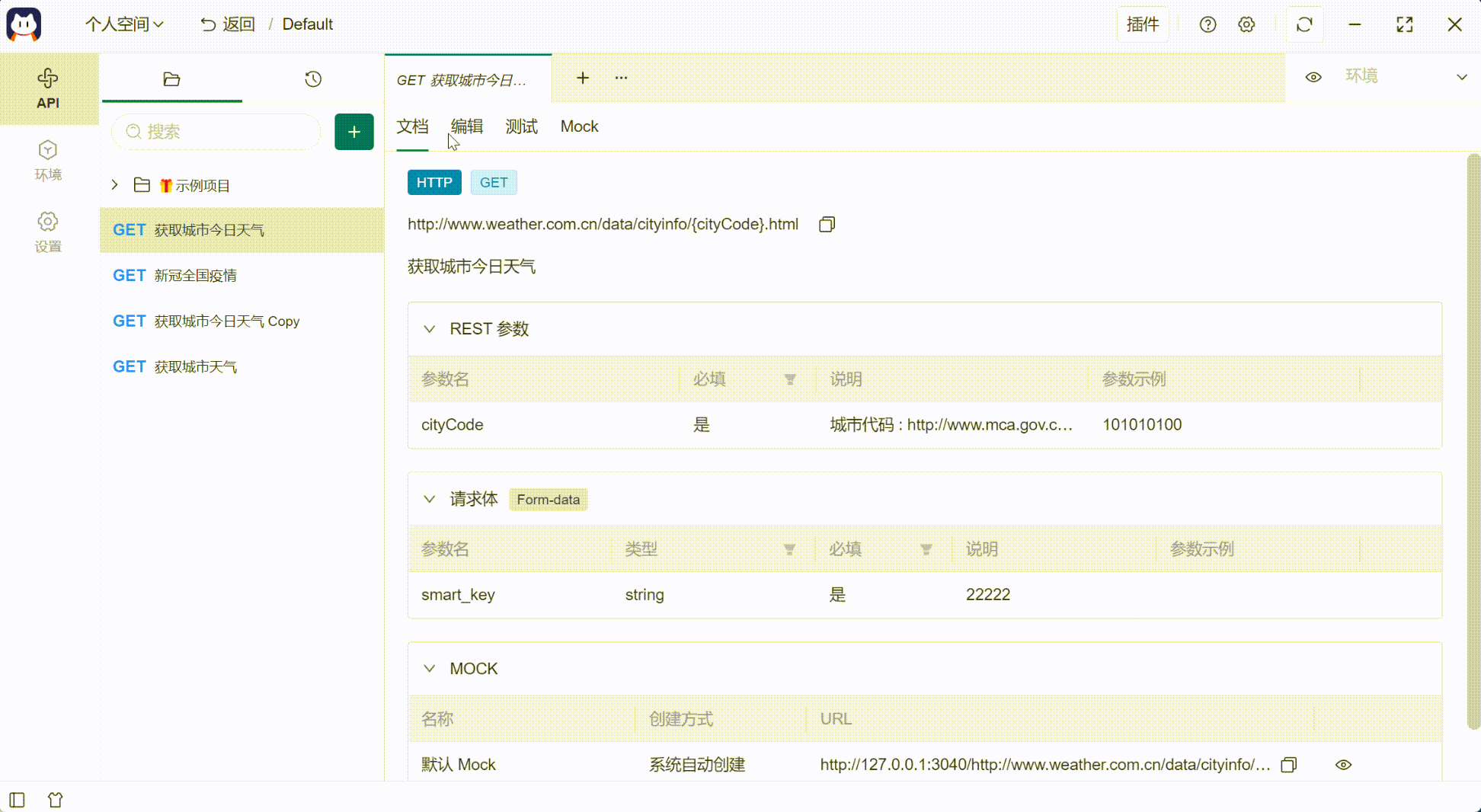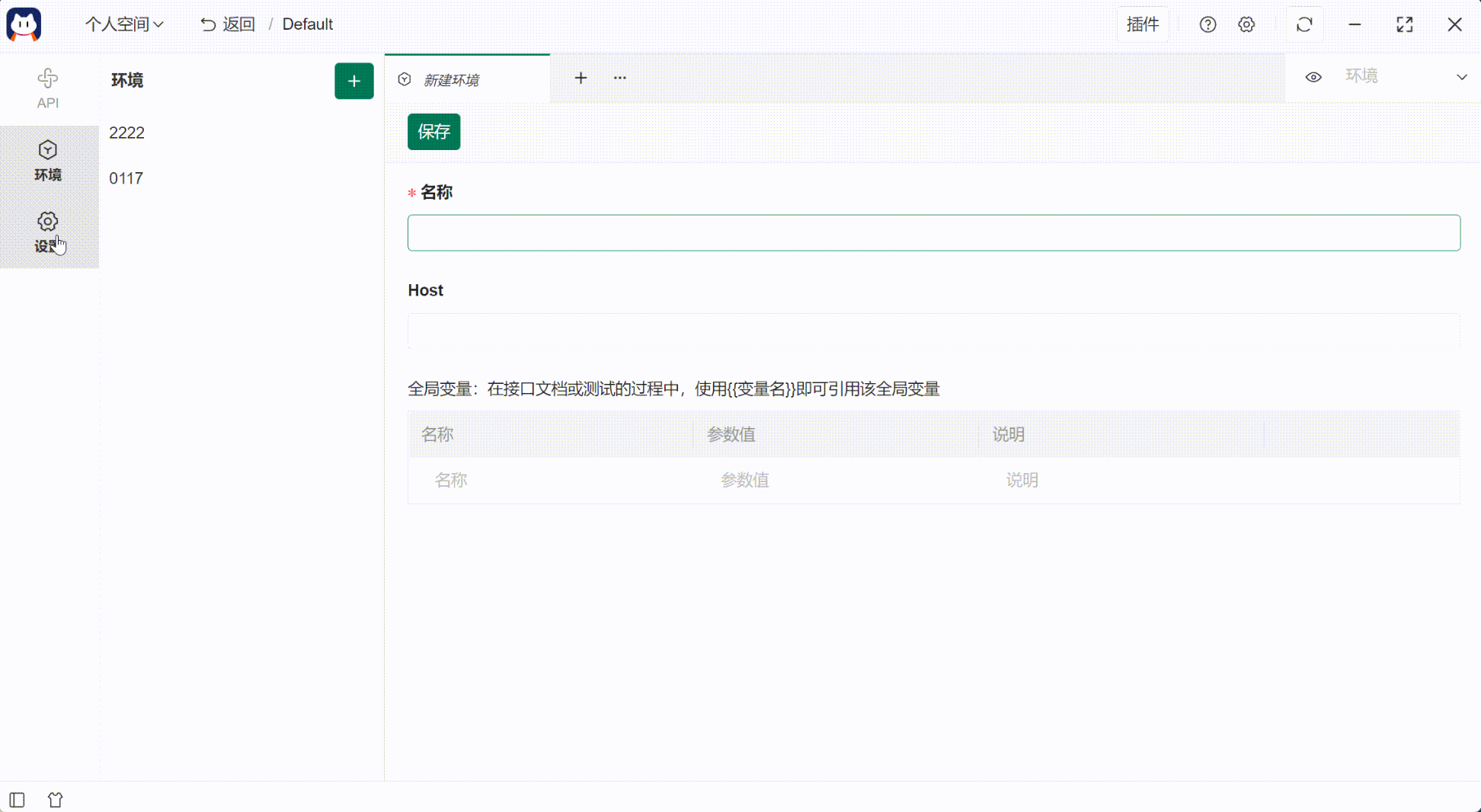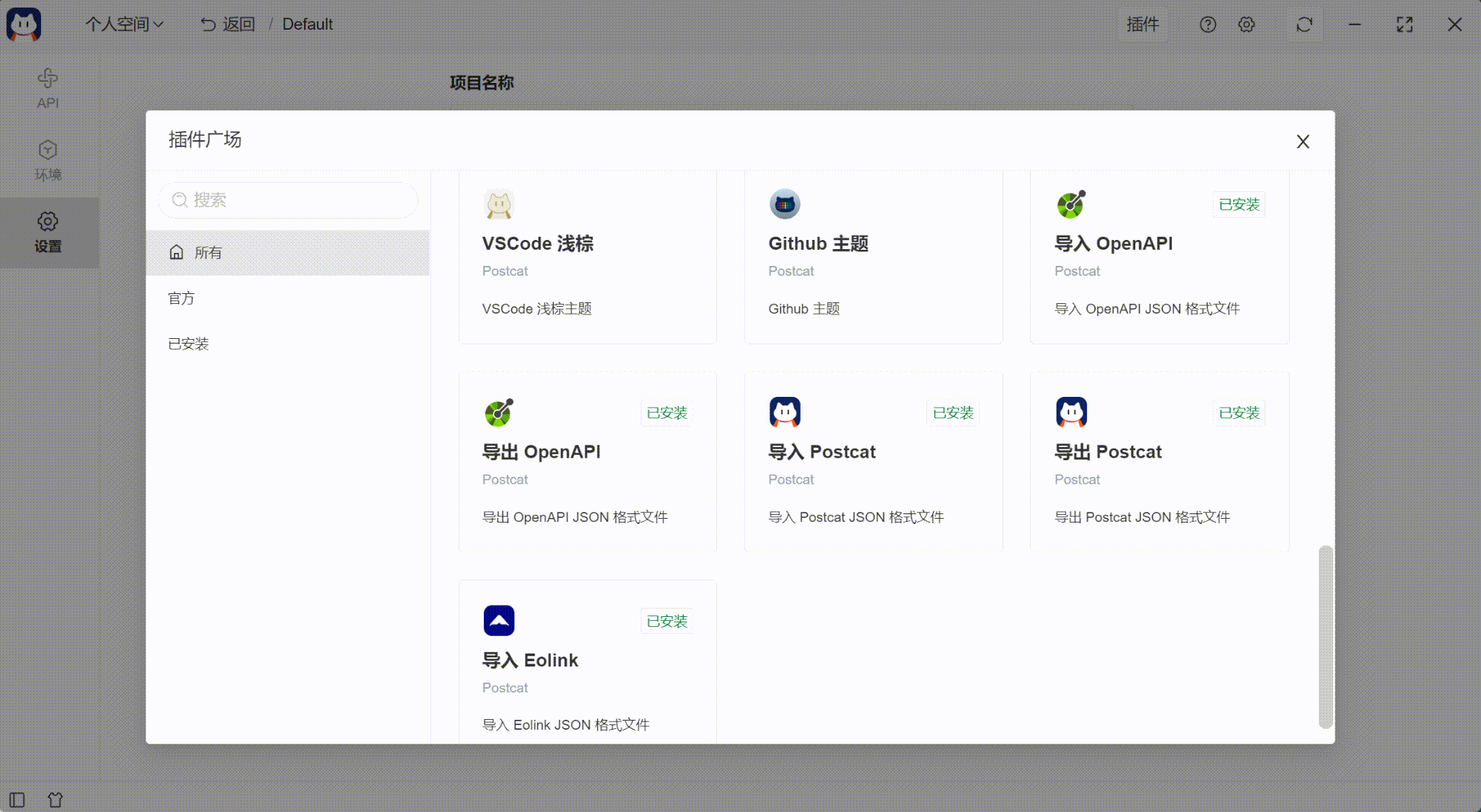
从没想过开源 API 工具的 Mock 功能,这么好用
很多时候,接口尚未开发完成,在系统交互双方定义好接口之后,我们可以提前进行开发和测试,并不依赖上游系统的开发实现。 通过使用Mock模拟数据接口,我们即可在只开发了UI的情况下,无须服务端的开发就可以进行…...

智慧教室--智能管控系统
智慧教室系统是一款基于AIOT数字化平台的智能教育解决方案,该系统实现了全面数字化、自动化管理和智能化控制,可大大提高教学效率和质量,为学生带来更加优质的教育体验。智能管控是智慧教室系统的核心功能之一。通过物联网技术,将…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
