C. Build Permutation【整数理论、构造、思维】
链接
理论基础
结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。
构造⌈n⌉2构造\lceil \sqrt{n}\rceil^2构造⌈n⌉2
∵n⩽⌈n⌉\because \sqrt n \leqslant \lceil \sqrt{n}\rceil∵n⩽⌈n⌉
∴n⩽⌈n⌉2\therefore n\leqslant \lceil \sqrt{n}\rceil^2∴n⩽⌈n⌉2
⌈n⌉⩽n+1\lceil \sqrt{n}\rceil \leqslant \sqrt{n} + 1⌈n⌉⩽n+1
⌈n⌉2⩽n+2n+1\lceil \sqrt{n}\rceil^2 \leqslant n+2\sqrt n+1⌈n⌉2⩽n+2n+1
何时2n⩾n+2n+1何时2n\geqslant n+2\sqrt n+1何时2n⩾n+2n+1
即n−2n−1⩾0即n-2\sqrt n-1\geqslant0即n−2n−1⩾0
(n−1)2⩾2(\sqrt n-1)^2\geqslant 2(n−1)2⩾2
当n⩾7的时候成立,而且取不到等号当n\geqslant 7的时候成立,而且取不到等号当n⩾7的时候成立,而且取不到等号
然后枚举0到6所有数0123456发现均可以找到不到2n的平方数然后枚举0到6所有数0~1~2~3~4~5~6发现均可以找到不到2n的平方数然后枚举0到6所有数0 1 2 3 4 5 6发现均可以找到不到2n的平方数
分别为−−−−−−0126543分别为------0~1~2~6~5~4~3分别为−−−−−−0 1 2 6 5 4 3
分析
这里从最后的数开始寻找,[n, 2n],必定有一个平方数,与这个数配对的数可以是0~n的所有数,我们从后往前配对,一旦配对成功就倒置使得这些数的和均为平方数即可。面对剩余的序列如法炮制,同样是从最后一个开始找然后配对使得这些数的和均在以最后一个数为n的[n, 2n]区间内的一个数,由于倒置的和均等于头尾的和所有中间这部分倒置的和就是合法的。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (p << 1)
#define rs (p << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5 + 5;
int vis[N];
bool check(int x) {int sq = sqrt(x);return sq * sq == x;
}
void solve() {int n;cin >> n;for (int i = 0; i < n; i++) vis[i] = 0;map<int, int> mp; for (int i = n - 1; i >= 0; i--) {if (vis[i]) continue;//如果已经配对过的话int p = i;//从这个点开始往前找while (!check(p + i)) p--;//找到第一个恰好是平方的数int sum = p + i;//注意这里是ifor (int j = p; j <= i; j++) {//到i不是到n-1vis[j] = 1;mp[j] = sum - j;}}for (int i = 0; i < n; i++) {cout << mp[i] << " \n"[i == n - 1];}
}
int main(){ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) solve();return 0;
}
相关文章:

C. Build Permutation【整数理论、构造、思维】
链接 理论基础 结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。 构造⌈n⌉2构造\lceil \sqrt{n}\rceil^2构造⌈…...
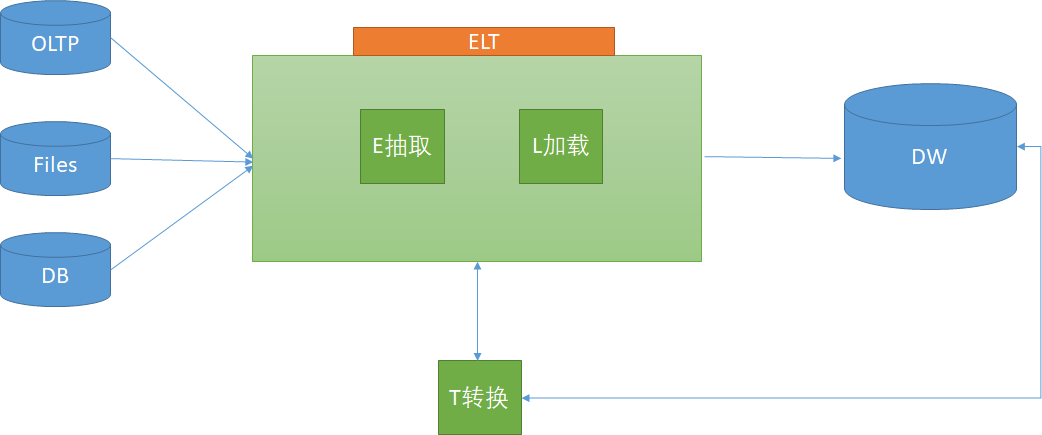
关于ETL的两种架构(ETL架构和ELT架构)
ETL,是英文 Extract-Transform-Load 的缩写,用来描述将数据从来源端经过抽取(extract)、转换(transform)、加载(load)至目的端的过程。ETL一词较常用在数据仓库,但其对象…...

android系统目录
环境:android studio引入android系统源码android和ubuntu策略路由的差异android源码编译问题(单编)repo(android源码)命令使用和注意事项wifi:wifi的加密类型梳理android11 wifisetting 流程跟踪android wifi热点settingandroid n…...

【C/C++】中【typedef】用法大全
总结一下typedef用法,一共七种,分别是:为基本数据类型起别名、为结构体起别名、为指针类型起别名、为数组类型起别名、为枚举类型起别名、为模版函数起别名。 目录 一、为基本数据类型起别名 二、为结构体起别名 三、为指针类型起别名 四…...

超实用的公众号运营攻略分享,纯干货
很多小伙伴抱怨,公众号运营真的越来越难做了! 每天会因为少得可怜的阅读量发愁,每天会因为纠结写什么选题发愁,每天更会因为公众号没有什么起色而感到无力。 现阶段公众号运营趋于饱和状态,公众号创建门槛低…...
编写NodeJs脚本实现接口请求
要编写运行脚本,需要先搭建开发环境 环境搭建 nodeJs脚本运行,当然需要先安装nodejs环境 官方地址在这里: nodejs官网 打开官网地址,可以看到下面一句话: Node.js is an open-source, cross-platform JavaScript runtime environment. 在打开的页面,可以直接下载最新的…...

【无人机】回波状态网络(ESN)在固定翼无人机非线性控制中的应用(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

YAML 文件简介
简介 我们在安装 kubernetes 集群的时候使用了一些 YAML 文件来创建相关的资源,但是对 YAML 文件还是非常陌生。所以我们先来简单看一看 YAML 文件是如何工作的,并使用 YAML 文件来定义一个 kubernetes pod,然后再来定义一个 kubernetes dep…...
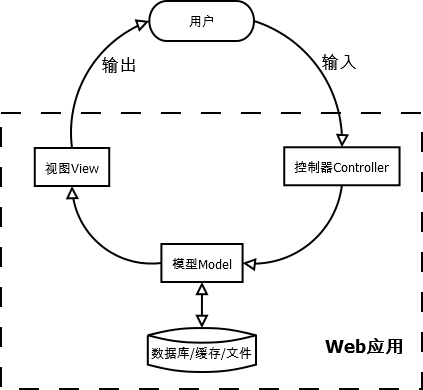
Python四大主题之一【 Web】 编程框架
目前Python的网络编程框架已经多达几十个,逐个学习它们显然不现实。但这些框架在系统架构和运行环境中有很多共通之处,本文带领读者学习基于Python网络框架开发的常用知识,及目前的4种主流Python网络框架:Django、Tornado、Flask、Twisted。 …...
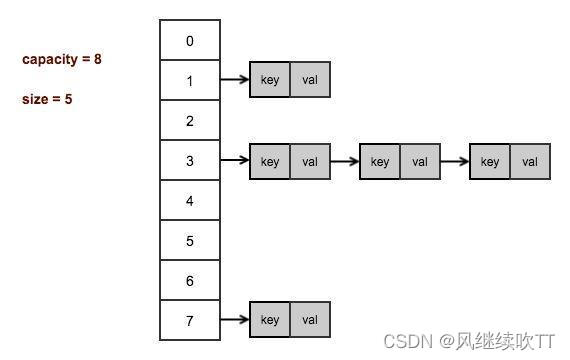
【C++】哈希表
1. unordered系列关联式容器 在C98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到 ,即最差情况下需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好的查询是,进行…...
深度学习入门(六十七)循环神经网络——注意力机制
深度学习入门(六十七)循环神经网络——注意力机制前言循环神经网络——注意力机制课件心理学注意力机制注意力机制是显式地考虑随意线索非参注意力池化层Nadaraya-Watson 核回归:总结教材(注意力提示)1 生物学中的注意…...
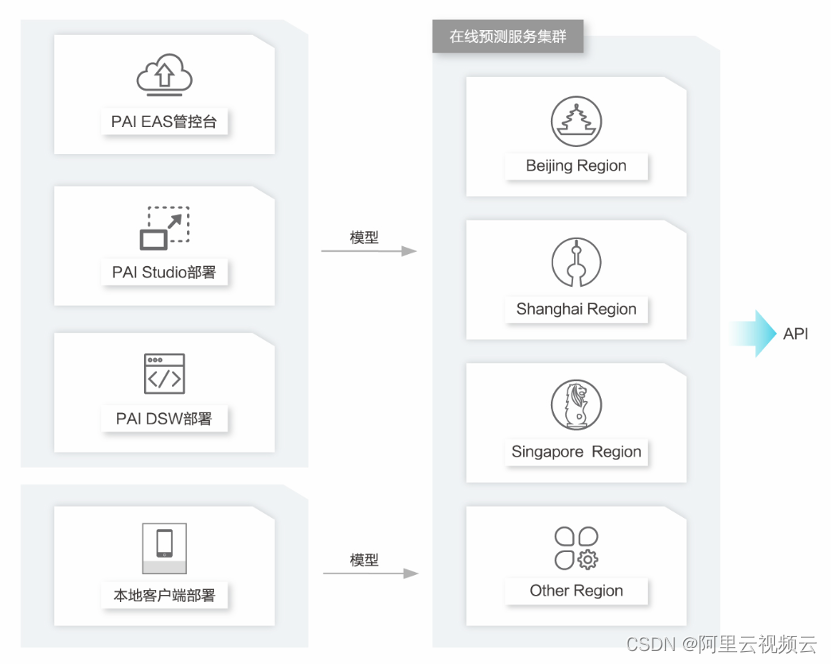
阿里云云通信风控系统的架构与实践
作者:铭杰 阿里云云通信创立于 2017 年,历经 5 年发展已经孵化出智能消息、智能语音、隐私号、号码百科等多个热门产品。目前,已成为了国内云通信市场的领头羊,在国际市场上服务范围也覆盖了 200 多个国家。随着业务的不断壮大&am…...

【性能测试】loadrunner(一)知识准备
【性能测试】loadrunner(一)知识准备 目录:导读 1.0. 前言 1.1 性能测试术语介绍 1.2 性能测试分类 1.3 HTTP我们需要知道的 1.4 Loadrunner 12.55安装 1.0. 前言 在性能测试中,牵扯到了许多比较杂的知识点,…...
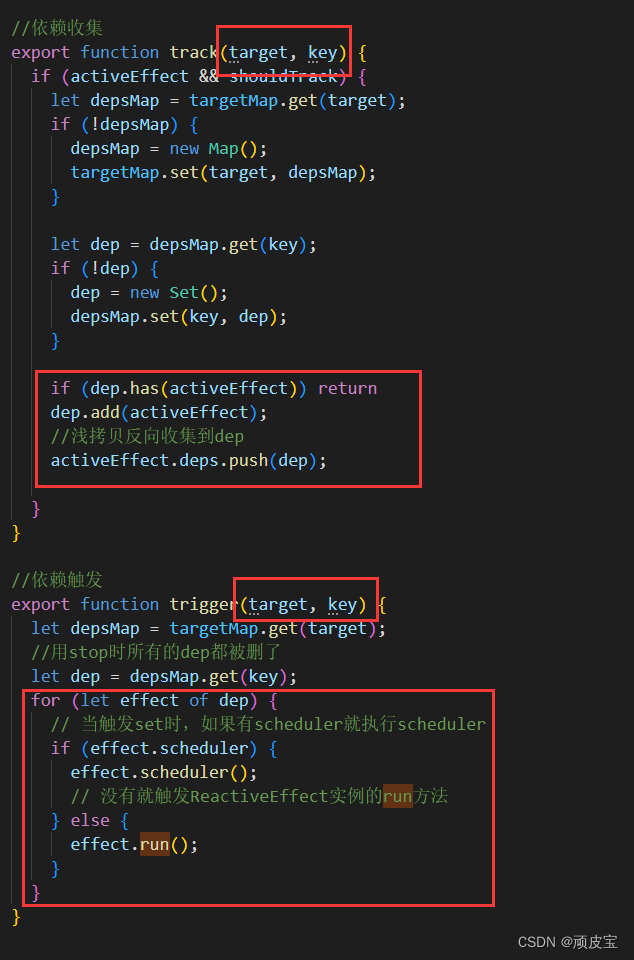
【Vue3源码】第五章 ref的原理 实现ref
【Vue3源码】第五章 ref的原理 实现ref 上一章节我们实现了reactive 和 readonly 嵌套对象转换功能,以及shallowReadonly 和isProxy几个简单的API。 这一章我们开始实现 ref 及其它配套的isRef、unRef 和 proxyRefs 1、实现ref 接受一个内部值,返回一…...
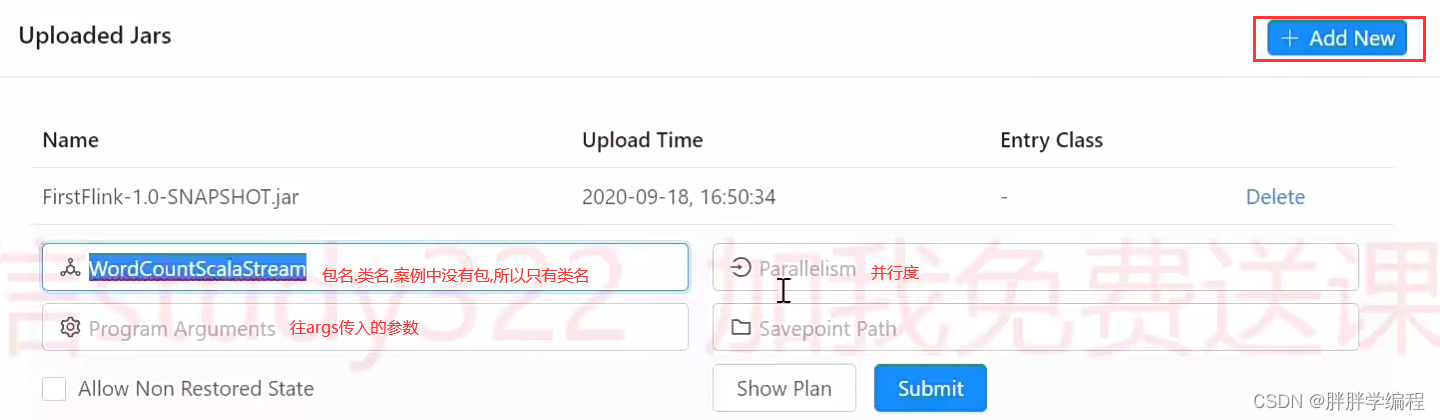
[Flink]部署模式(看pdf上的放上面)
运行一个wordcountval dataStream: DataStream[String] environment.socketTextStream("hadoop1", 7777) //流式数据不能进行groupBy,流式数据要来一条处理一次.0表示第一个元素,1表示第二个元素 //keyBy(0)根据第一个元素进行分组 val out: DataStream[(String, In…...

Linux 查看 CPU 信息,机器型号,内存等信息
平时用的可能少,但需要记住,使用的命令,转载https://my.oschina.net/hunterli/blog/140783,以记录学习 系统 # uname -a # 查看内核/操作系统/CPU信息 # head -n 1 /etc/issue # 查看操作系统版本 # cat /proc/…...
)
三维量子力学 量子力学(3)
动量ppp有三个分量,为pxp_xpx等。它们分别满足与位置坐标的对易关系,比如px−iℏ∂∂xp_x-i\hbar\frac{\partial }{\partial x}px−iℏ∂x∂。可以用位置坐标梯度算符表示即p−iℏ∇\bm{p}-i\hbar\nablap−iℏ∇。位置矢量用r\bm{r}r表示。 在d3r…...

Blazor入门100天 : 身份验证和授权 (6) - 使用 FreeSql orm 管理ids数据
目录 建立默认带身份验证 Blazor 程序角色/组件/特性/过程逻辑DB 改 Sqlite将自定义字段添加到用户表脚手架拉取IDS文件,本地化资源freesql 生成实体类,freesql 管理ids数据表初始化 Roles,freesql 外键 > 导航属性完善 freesql 和 bb 特性 本节源码 https://github.com/…...

Java文件IO操作:File类的相关内容
Java文件IO操作一、File类1.相对路径和绝对路径2.路径分隔符(同一路径下、多个路径下)3.实例化4.常见方法一、File类 File类继承自Object类,实现了Serializable接口和Comparable接口; File类属于java.io包; File类是文…...
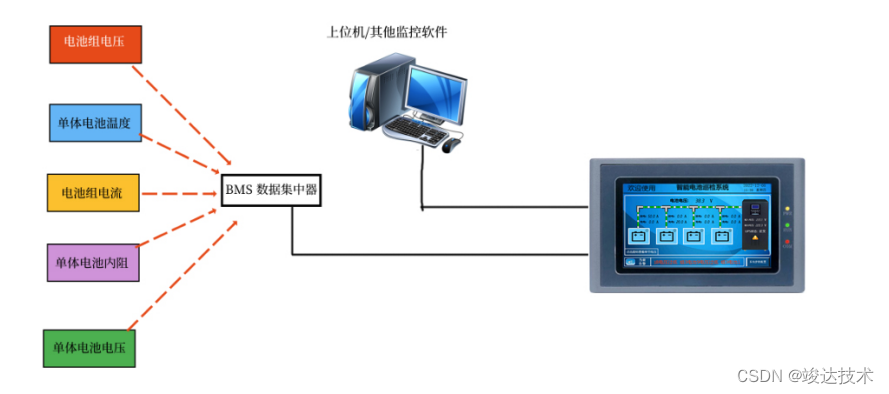
竣达技术 | 巡检触摸屏配合电池柜,电池安全放首位!
机房蓄电池常见的故障 1.机房电池着火和爆炸 目前在数据机房蓄电池爆炸着火事故频发,导致业主损失严重。一般机房电池是由于其中一节电池裂化后未妥善管理,电池急剧恶化导致爆炸着火。由于电池是串联及并联在使用,只要一节着火燃烧整片瞬间…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
