想要精通算法和SQL的成长之路 - 验证二叉树
想要精通算法和SQL的成长之路 - 验证二叉树
- 前言
- 一. 验证二叉树
- 1.1 并查集
- 1.2 入度以及边数检查
前言
想要精通算法和SQL的成长之路 - 系列导航
并查集的运用
一. 验证二叉树
原题链接
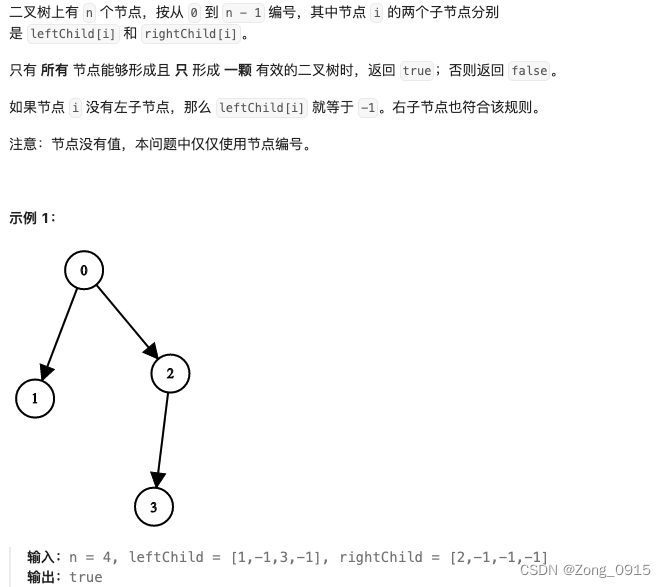
思路如下:
-
对于一颗二叉树,我们需要做哪些校验?
-
首先这颗树不可以成环,如图:

-
其次,这颗树的边数量,应该等于 n -1。如下图就是错的:

-
存在一个根节点,它的入度为0,其他所有的节点,入度都不能够超过1。
那么针对以上几点,我们可以分别来考虑。我们同时遍历一次左右节点数组。值不是-1的话,说明该端连接的节点非空。
- 我们用一个
int[] inDegree数组代表入度。对应值非-1的时候,入度加1。 - 用一个
edges变量代表无向边数,只要值非-1,变数+1。 - 同时在遍历的过程中,针对值非-1的情况,我们将左右两端的节点进行合并。这一块使用并查集数据结构。最终合并完之后,根节点数应该只有一个。
那么我们先写并查集的数据结构。
1.1 并查集
class UnionFind {private int[] parent;private int[] rank;private int sum;public UnionFind(int n) {rank = new int[n];parent = new int[n];// 初始化,每个节点的根节点指向其本身for (int i = 0; i < n; i++) {parent[i] = i;}// 这里指的是根节点数量sum = n;}public int find(int x) {while (x != parent[x]) {x = parent[x];}return x;}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);// 如果两个元素的根节点一致,不需要合并if (rootX == rootY) {return;}// 如果根节点 rootX 的深度 > rootY。if (rank[rootX] > rank[rootY]) {// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中rank[rootX] += rank[rootY];// 同时改变rootY的根节点,指向rootX。parent[rootY] = rootX;} else {// 反之rank[rootY] += rank[rootX];parent[rootX] = rootY;}sum--;}
}
1.2 入度以及边数检查
public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {int[] inDegree = new int[n];UnionFind unionFind = new UnionFind(n);// 边数int edges = 0;for (int i = 0; i < n; i++) {int left = leftChild[i];int right = rightChild[i];if (left != -1) {// 入度数+1,并且合并左右两端。同时边数+1inDegree[left]++;unionFind.union(i, left);edges++;}if (right != -1) {inDegree[right]++;unionFind.union(i, right);edges++;}}// 判断边数是否等于 n -1 if (edges != n - 1) {return false;}// 判断入度数是否都是 <=1,这里统计入度数 > 1的节点个数int count = 0;for (int i = 0; i < n; i++) {if (inDegree[i] > 1) {count++;}}// 不该存在入度数 >1 的节点,如果存在,返回falseif (count > 0) {return false;}// 判断是否存在环,此时根节点只能存在一个return unionFind.sum == 1;
}
最终代码如下:
public class Test1361 {public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {int[] inDegree = new int[n];UnionFind unionFind = new UnionFind(n);int edges = 0;for (int i = 0; i < n; i++) {int left = leftChild[i];int right = rightChild[i];if (left != -1) {inDegree[left]++;unionFind.union(i, left);edges++;}if (right != -1) {inDegree[right]++;unionFind.union(i, right);edges++;}}// 判断边数是否相等if (edges != n - 1) {return false;}// 判断入度数是否都是 <=1int count = 0;for (int i = 0; i < n; i++) {if (inDegree[i] > 1) {count++;}}if (count > 0) {return false;}// 判断是否存在环return unionFind.sum == 1;}class UnionFind {private int[] parent;private int[] rank;private int sum;public UnionFind(int n) {rank = new int[n];parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}sum = n;}public int find(int x) {while (x != parent[x]) {x = parent[x];}return x;}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);// 如果两个元素的根节点一致,不需要合并if (rootX == rootY) {return;}// 如果根节点 rootX 的深度 > rootY。if (rank[rootX] > rank[rootY]) {// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中rank[rootX] += rank[rootY];// 同时改变rootY的根节点,指向rootX。parent[rootY] = rootX;} else {// 反之rank[rootY] += rank[rootX];parent[rootX] = rootY;}sum--;}}
}
相关文章:

想要精通算法和SQL的成长之路 - 验证二叉树
想要精通算法和SQL的成长之路 - 验证二叉树 前言一. 验证二叉树1.1 并查集1.2 入度以及边数检查 前言 想要精通算法和SQL的成长之路 - 系列导航 并查集的运用 一. 验证二叉树 原题链接 思路如下: 对于一颗二叉树,我们需要做哪些校验? 首先…...
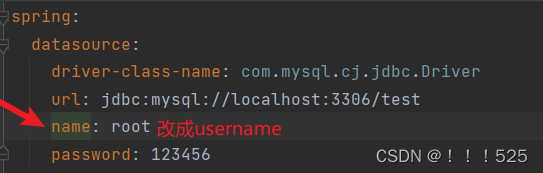
ERROR 6400 --- [ main] com.zaxxer.hikari.pool.HikariPool : root - Exception
在引用的日志中,报告了Hikari连接池初始化期间的异常。具体异常信息是"Exception during pool initialization"。这个异常可能是由于与MySQL数据库的通信链接失败导致的。在引用中也提到了与SSL连接相关的错误。 根据引用中提供的代码,可以看到…...

CART算法解密:从原理到Python实现
目录 一、简介CART算法的背景例子:医疗诊断 应用场景例子:金融风控 定义与组成例子:电子邮件分类 二、决策树基础什么是决策树例子:天气预测 如何构建简单的决策树例子:动物分类 决策树算法的类型例子:垃圾…...
C++项目:【高并发内存池】
文章目录 一、项目介绍 二、什么是内存池 1.池化技术 2.内存池 3.内存池主要解决的问题 4.malloc 三、定长的内存池 四、高并发内存池整体框架设计 1.高并发内存池--thread cache 1.1申请内存: 1.2释放内存: 1.3用TLS实现thread cache无锁访…...

[论文笔记]BitFit
引言 今天带来一篇参数高效微调的论文笔记,论文题目为 基于Transformer掩码语言模型简单高效的参数微调。 BitFit,一种稀疏的微调方法,仅修改模型的偏置项(或它们的子集)。对于小到中等规模数据,应用BitFit去微调预训练的BERT模型能达到(有时超过)微调整个模型。对于大规…...

浅谈yolov5中的anchor
默认锚框 YOLOv5的锚框设定是针对COCO数据集中大部分物体来拟定的,其中图像尺寸都是640640的情况。 anchors参数共3行: 第一行是在最大的特征图上的锚框 第二行是在中间的特征图上的锚框 第三行是在最小的特征图上的锚框 在目标检测中,一…...
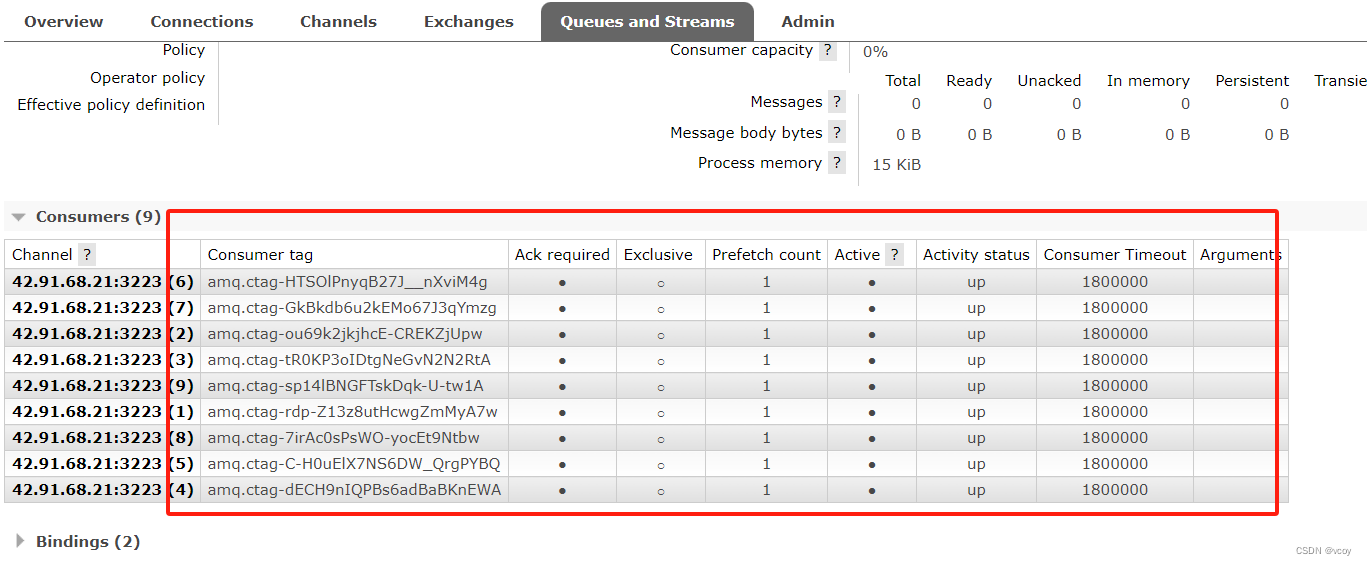
RabbitMQ-工作队列
接上文 RabbitMQ-死信队列 1 工作队列模式 xx模式只是一种设计思路,并不是指具体的某种实现,可理解为实现XX模式需要怎么去写业务代码。 之前的是简单的一个消费者一个生产者模式,下边是一个生产者多个消费者的情况: 这里先定义两…...

网站安全防护措施
网络安全的重要性在网站和app的发展下已经被带到了全新的高度,已然成为各大运维人员工作里不可或缺的环节,重视网络安全能给我们的网站带来更好的口碑,也能为企业生产创造更稳定的环境。下面我们一起来看看有哪些是我们运维人员能够做的。 1、…...
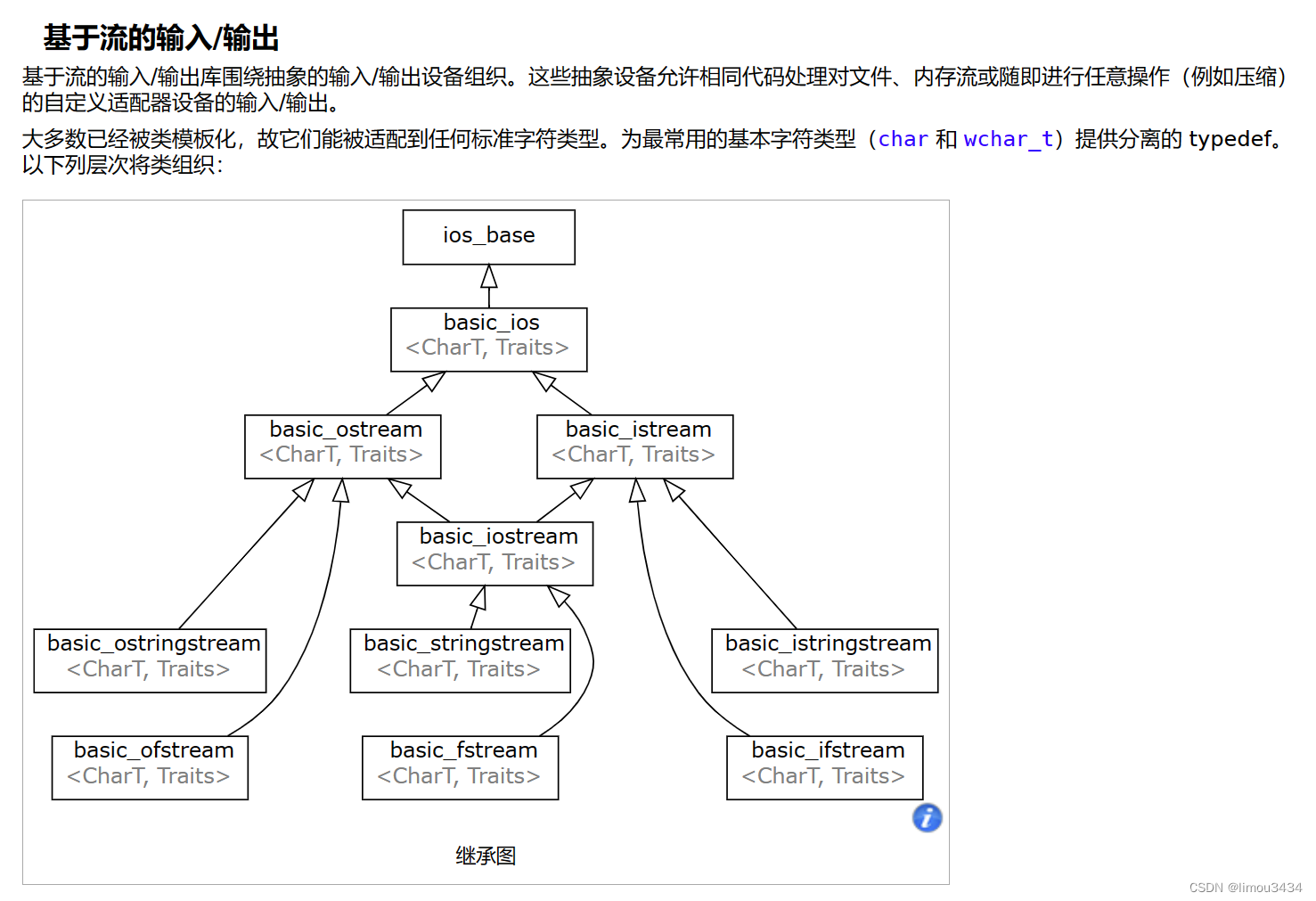
C++的继承基础和虚继承原理
1.继承概念 “继承”是面向对象语言的三大特性之一(封装、继承、多态)。 继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段,它允许程序员在保持原有类特性基础上进行扩展,增加功能&…...
)
第三章:最新版零基础学习 PYTHON 教程(第十三节 - Python 运算符—Python 中的运算符函数 - 套装2)
Python 中的运算符函数 - 套装1 本文将讨论更多功能。 1. setitem(ob, pos, val):- 该函数用于在容器中的 特定位置分配值。操作 – ob[pos] = val 2. delitem(ob, pos):- 该函数用于删除容器中 特定位置的值。 操作 – del ob[pos] 3. getitem(ob, pos)&#x...
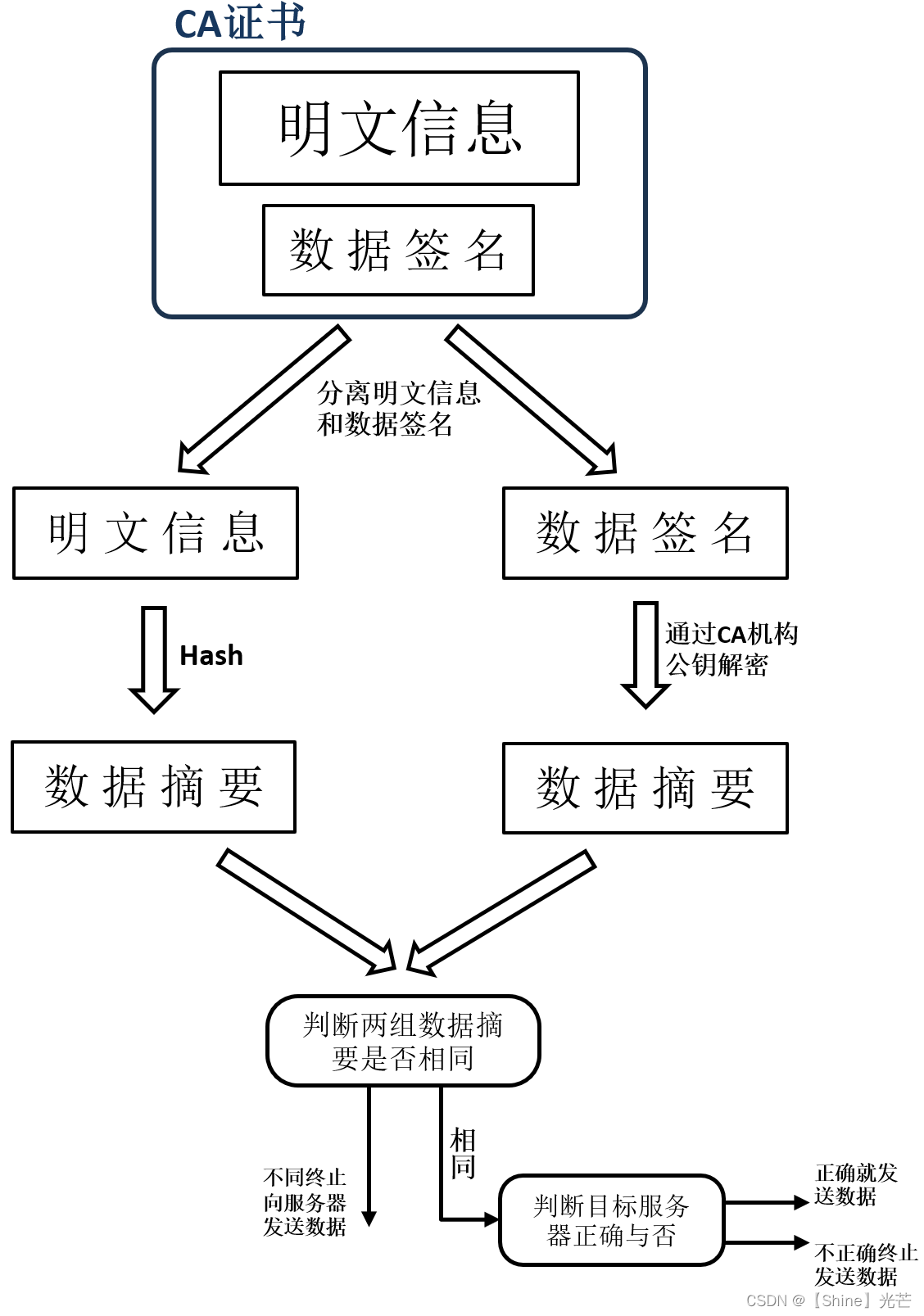
Linux网络编程:详解https协议
目录 一. https协议概述 二. 中间人截获 三. 常见的加密方法 3.1 对称加密 3.2 非对称加密 四. 数据摘要和数据签名的概念 五. https不同加密方式的安全性的探究 5.1 使用对称加密 5.2 使用非对称加密 5.3 非对称加密和对称加密配合使用 六. CA认证 七. 总结 一.…...

LLVM IR 文档 专门解释 LLVM IR
https://llvm.org/docs/LangRef.html#phi-instruction...
免费服务器搭建网盘教程,给电脑挂载500G磁盘
免费服务器搭建网盘教程,给电脑挂载500G磁盘 请勿注册下载,注册下载是空白文件,使用免登录下载 免费搭建网盘教程,给电脑挂载500G磁盘 其他按照下载教程操作教程代码: 下载下来的文件pancn 文件拖到您创建的容器 手机的话点击…...
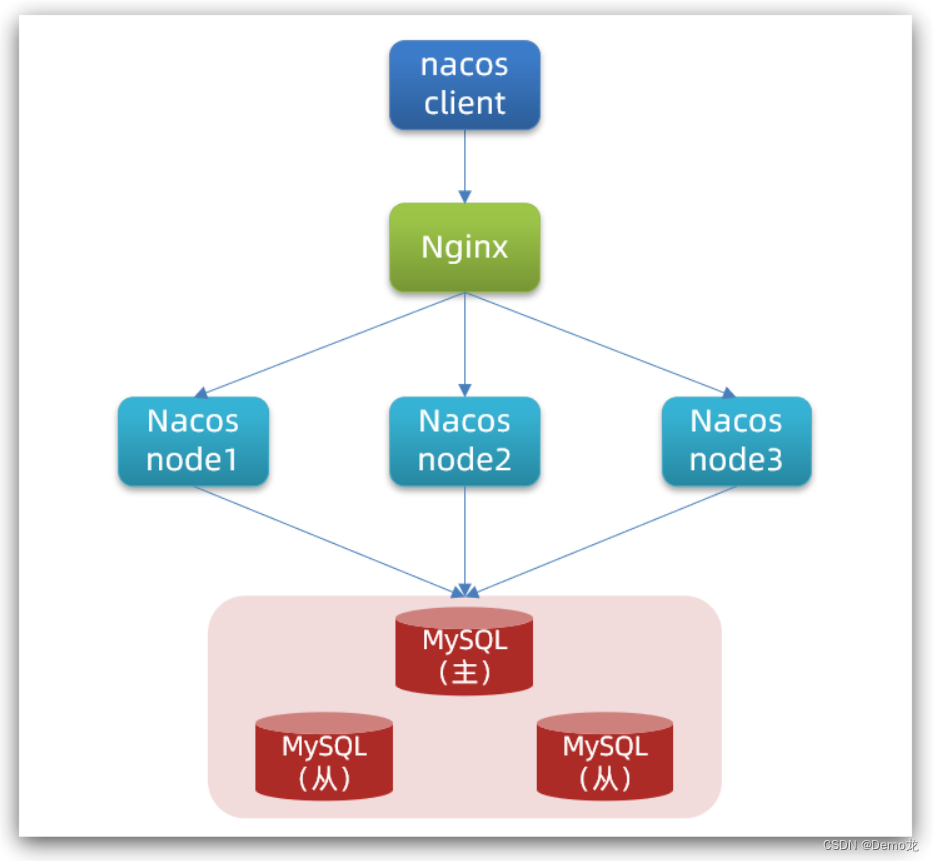
【Java】微服务——Nacos配置管理(统一配置管理热更新配置共享Nacos集群搭建)
目录 1.统一配置管理1.1.在nacos中添加配置文件1.2.从微服务拉取配置1.3总结 2.配置热更新2.1.方式一2.2.方式二2.3总结 3.配置共享1)添加一个环境共享配置2)在user-service中读取共享配置3)运行两个UserApplication,使用不同的pr…...
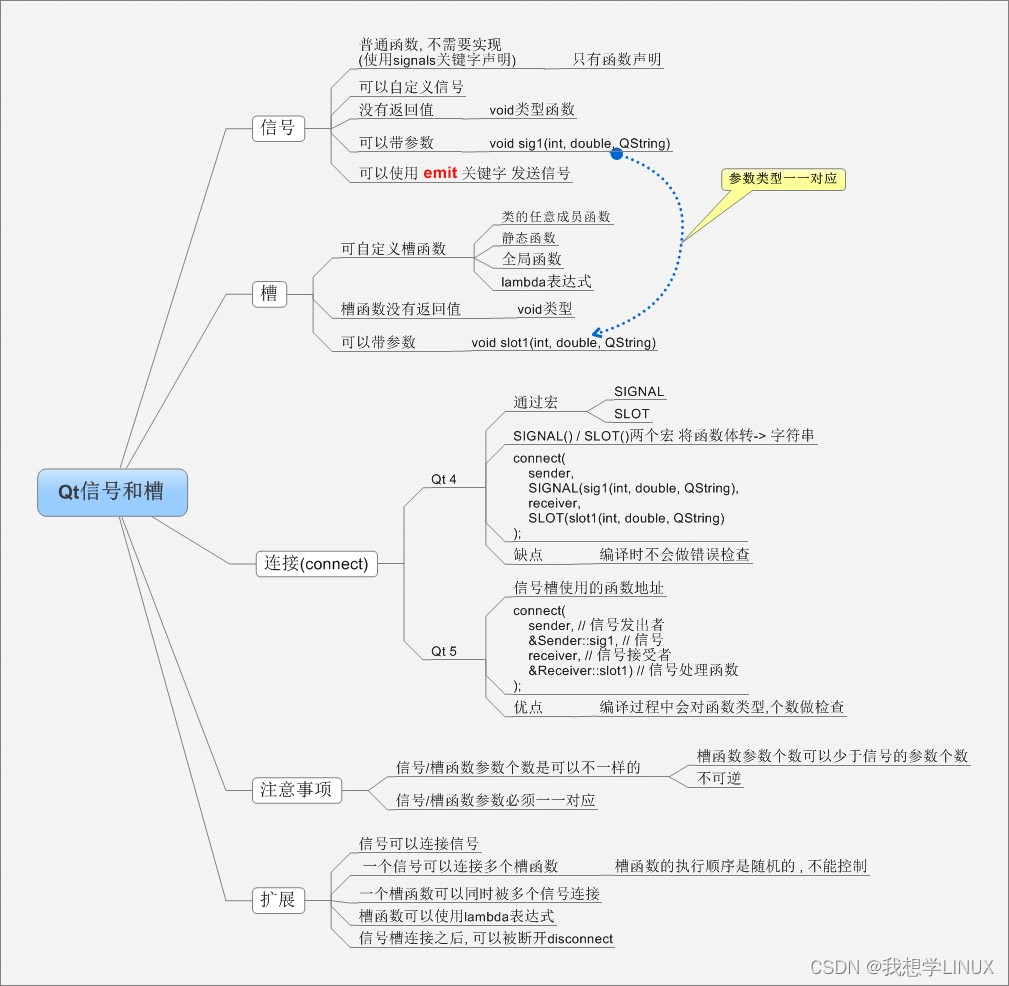
QT基础入门——信号和槽机制(二)
前言: 在Qt中,有一种回调技术的替代方法:那就是信号和槽机制。当特定事件发生时,会发出一个信号。Qt的小部件中有许多预定义的信号,但我们可以将小部件子类化,向它们添加自定义的信号。槽是响应特定信号的…...

黑豹程序员-架构师学习路线图-百科:JavaScript-网页三剑客
文章目录 1、为什么需要JavaScript2、发展历史3、什么是JavaScript3.1、JavaScript介绍3.2、JavaScript内部结构3.3、主要功能 4、TypeScript 1、为什么需要JavaScript 前面我们已经了解了网页三剑客的HTML和CSS,已经明确了它们的职责。 HTML负责页面的展现&#x…...

三、互联网技术——IP子网划分
文章目录 一、IP地址基础1.1 IP地址分类1.2 网络掩码/子网掩码 二、子网划分VLSM2.1 为什么要进行子网划分2.2 怎么进行子网划分2.3 子网划分原理2.4 例题一2.5 例题二2.6 例题三2.6 例题四2.7 例题五2.8 例题六2.9 例题七2.10 例题八 三、无类域间路由CIDR3.1 例题一3.2 例题二…...

TinyWebServer学习笔记-log
为什么服务器要有一个日志系统? 故障排查和调试: 在服务器运行期间,可能会发生各种问题和故障,例如程序崩溃、性能下降、异常请求等。日志记录了服务器的运行状态、错误信息和各种操作,这些日志可以用来快速定位和排查…...

【kubernetes】CRI OCI
1 OCI OCI(Open Container Initiative):由Linux基金会主导,主要包含容器镜像规范和容器运行时规范: Image Specification(image-spec)Runtime Specification(runtime-spec)runC image-spec定义了镜像的格式,镜像的格式有以下几…...

竞赛 机器视觉opencv答题卡识别系统
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 答题卡识别系统 - opencv python 图像识别 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🥇学长这里给一个题目综合评分(每项满分5分…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
