深入剖析红黑树:优雅地平衡二叉搜索树

目录
- 一.红黑树的概念
- 二.插入操作
- 三.与AVL树的比较
一.红黑树的概念
在之前的学习中,我们了解了二叉搜索平衡树,AVL树通过控制每个结点中的平衡因子的绝对值不超过1,实现了一个高性能的树。而相较于AVL的高度平衡,红黑树觉得AVL为了平衡也付出了代价(插入和删除时进行了多次旋转),所以红黑树在控制平衡上面没有这么严格,只是要求,最长路径不超过最短路径的二倍。那红黑树又是如何控制实现的呢?接下来了解一下红黑树的性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的(任何路径上没有连续两个红结点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,也称为NIL结点)
二.插入操作
在我们了解红黑树的性质后,就需要分析相关代码看他如何实现的。首先我们看红黑树结点的定义:
因为map和set的底层使用红黑树实现了,为了之后方便,这里红黑树用了两个模板参数。
#include <iostream>using namespace std;enum Colour
{RED, BLACK
};template<class K,class V>
class RBTreeNode
{
public:RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};
结点定义中与AVL树差距不大,只是多了个用枚举定义的参数,用来指定是红结点还是黑结点。接下来讲解重点的插入操作:
首先因为红黑树也是二叉搜索树,所以要满足二叉搜索树的基本性质,再者是我们插入的结点的颜色先置为什么能让后面的调整更方便呢。如果黑色需要在后面依据性质4调整,插入红色的话依据性质3调整。明显是4更为复杂,所以我们插入颜色为红色。
bool Insert(const pair<K, V>& kv)
{if(_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;///开始调整颜色///开始调整颜色_root->_col = BLACK;return true;
}
上段代码是不涉及调整颜色,只保证二叉搜索树性质。下面开始分类讨论研究如何调整颜色。
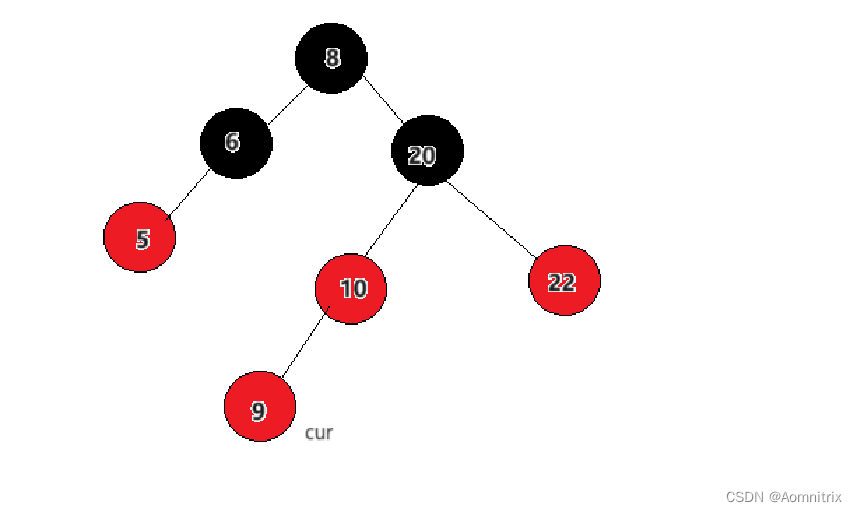
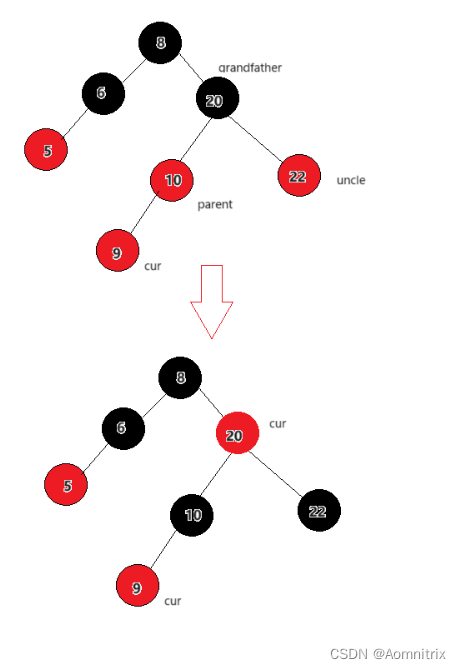
如上图所示,插入的cur结点是红色,这时出现了连续的两个红结点,所以就要进行调整。如果parent结点是黑色则不需要调整。我们把10结点和20结点称为parent和grandfather结点,22为uncle结点。
1.当uncle结点为红色时,变色然后继续向上调整
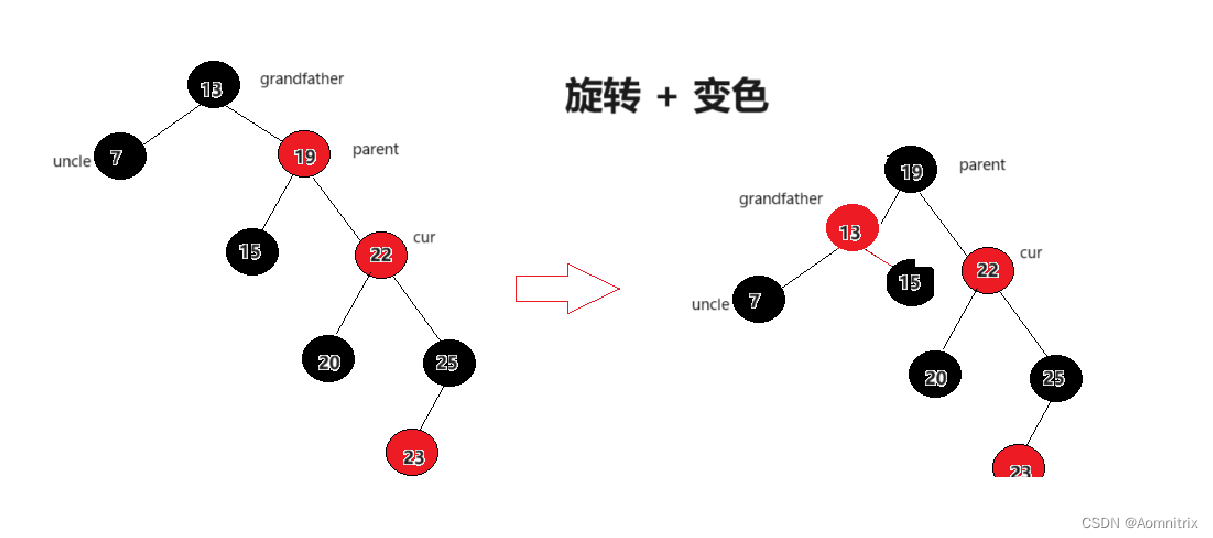
2.当uncle结点不存在时或者为黑时的处理方式相同:
完整代码如下:
bool Insert(const pair<K, V>& kv){if(_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//叔叔存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else // 叔叔不存在或者为黑都是旋转+变色{if (cur == parent->_left){RevoR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RevoL(parent);RevoR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}}}else{Node* uncle = grandfather->_left;//叔叔存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else // 叔叔不存在或者为黑都是旋转+变色{if (cur == parent->_left){RevoR(parent);RevoL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}else{RevoL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return true;}void RevoL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;//无论curleft是否为空都要执行这一步if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RevoR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright){curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (_root == parent)//等价于 ppnode == nullptr{_root = cur;cur->_parent = nullptr;}else{cur->_parent = ppnode;if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}}}
三.与AVL树的比较
红黑树和AVL树的插入效率O(logN),只是红黑树不像AVL追求如此平衡,所以旋转次数会少,并且实现也较简单。所以在实践中大都使用红黑树。之后我们还是使用红黑树模拟实现map和set。
相关文章:

深入剖析红黑树:优雅地平衡二叉搜索树
目录 一.红黑树的概念二.插入操作三.与AVL树的比较 一.红黑树的概念 在之前的学习中,我们了解了二叉搜索平衡树,AVL树通过控制每个结点中的平衡因子的绝对值不超过1,实现了一个高性能的树。而相较于AVL的高度平衡,红黑树觉得AVL为…...
C10K问题:高并发模型设计
一、循环服务器模型 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <errno.h> #include <unistd.h> #include <signal.h> #include <sys/types.h> #include <sys/socket.h> //*******// #include &l…...

哈希/散列--哈希表[思想到结构][==修订版==]
文章目录 1.何为哈希?1.1百度搜索1.2自身理解1.3哈希方法/散列方法1.4哈希冲突/哈希碰撞1.5如何解决?哈希函数的设计 2.闭散列和开散列2.1闭散列/开放定址法2.2开散列/链地址法/开链法1.概念2.容量问题3.字符串问题4.开散列性能测试5.开散列与闭散列比较 3.代码实现[配备详细…...

成都建筑模板批发市场在哪?
成都作为中国西南地区的重要城市,建筑业蓬勃发展,建筑模板作为建筑施工的重要材料之一,在成都也有着广泛的需求。如果您正在寻找成都的建筑模板批发市场,广西贵港市能强优品木业有限公司是一家值得关注的供应商。广西贵港市能强优…...

亨元模式 结构型模式之六
1.定义 享元模式是一种结构型设计模式, 它允许你在消耗少量内存的情况下支持大量对象。 2.滑滑梯问题 在说明亨元模式之前,我们先看看关于滑滑梯的程序设计。小区的楼下只有三个滑滑梯,但是想玩的小朋友却非常多。怎么设计计滑滑梯资源的管理…...

面试题: Spring中Bean的实例化和Bean的初始化有什么区别?
Spring中Bean的实例化和Bean的初始化有什么区别? 背景答案扩展知识什么是实例化什么是初始化 个人评价我的回答 背景 想换工作, 看了图灵周瑜老师的视频想记录一下, 算是学习结果的一个输出. 答案 Spring 在创建一个Bean对象时, 会先创建出一个Java对象, 会通过反射来执行…...

阻塞队列,生产者消费者模型
目标: 1. 认识与使用阻塞队列 2. 认识与实现消费者模型 目录 阻塞队列的特点 生产者消费者模型 生产者消费者模型的优点 阻塞队列实现该模型 阻塞队列的特点 1. 线程安全 2. 带有阻塞特性 (1)如果队列为空,继续出队列&a…...

【RCRL充放电时间相关计算】
一. 基础知识 L、C元件称为“惯性元件”,即电感中的电流、电容器两端的电压,都有一定的“电惯性”,不能突然变化。充放电时间,不光与L、C的容量有关,还与充/放电电路中的电阻R有关。RC电路的时间常数:τRC…...

C++ primer plus--输入、输出和文件
17 输入、输出和文件 17.1 C 输入和输出概述 C 把输入和输出看做字节流。输入时,程序从输入流中抽取字节;输出时,程序将字节插到输出流中。 缓冲区是内存中的临时存储区域,是程序与文件或其他 I/O 设备之间的桥梁。 17.2 使用…...

案例题--Web应用考点
案例题--Web应用考点 负载均衡技术微服务XML和JSON无状态和有状态真题 在选择题中没有考察过web的相关知识,主要就是在案例分析题中考察 负载均衡技术 应用层负载均衡技术 传输层负载均衡技术 就近的找到距离最近的服务器,并进行分发 使用户就近获取…...

MySQL的SQL 优化:提升数据库性能
1. 插入操作优化 1.1 使用多值插入 通常情况下,插入大量数据时,使用多值插入语句比逐行插入更高效。例如,将多个数据行打包成一个 INSERT 语句: INSERT INTO users (name, email) VALUES (Alice, aliceexample.com), (Bob, bob…...
【匠心打造】从0打造uniapp 可视化拖拽设计 c_o 第十篇
一、click one for uniapp置顶: 全部免费开源 (你商业用途也没关系,不过可以告诉我公司名或者项目名,放在官网上好看点。哈哈-_-) 二、写在之前 距离上一篇更新已经大约4个月了,公司的事情,自己的一些琐事一直没时间…...

BIT-5-操作符详解(C语言初阶学习)
1. 各种操作符的介绍。 2. 表达式求值 1. 操作符分类: 算术操作符 移位操作符 位操作符 赋值操作符 单目操作符 关系操作符 逻辑操作符 条件操作符 逗号表达式 下标引用、函数调用和结构成员 2. 算术操作符 - * / % 除了 % 操作符…...
【重拾C语言】三、分支程序设计(双分支和单分支程序设计、逻辑判断、多分支程序设计、枚举类型表示;典型例题:判断闰年和求一元二次方程根)
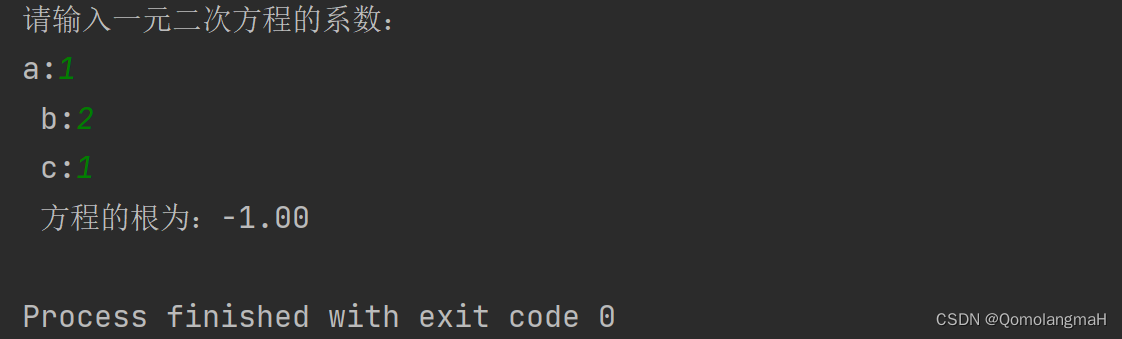
目录 前言 三、分支程序设计 3.1 判断成绩是否及格——双分支程序设计 3.2 成绩加上获奖信息—单分支程序设计 3.3 逻辑判断——布尔类型 3.4 获奖分等级——多分支程序设计 3.5 表示汽车种类——枚举类型 3.6 例题 3.6.1 例题——判断某个年份是否闰年 3.6.2 例题—…...

Shiro应用到Web Application
一、权限基础 a) 认证(你是谁?) 判断你(被认证者)是谁的过程。通常被认证者提供用户名和密码。 常见的认证包含如下几种: 匿名认证:允许访问资源,不做任何类型的安全检查。表单认证:访问资源之前,需要提…...

【POST请求-腾讯翻译君-爬虫案例】
原因:尝试多个在线翻译平台,由于返回数据存在加密原因(暂时不会解密),最总找到 ”腾讯翻译君“ 完成爬虫案例POST请求测试 案例测试网址 腾讯翻译 :https://fanyi.qq.com/ import requests import jsoncla…...

多卡片效果悬停效果
效果展示 页面结构 从页面的结构上看,在默认状态下毛玻璃卡片是有层次感的效果叠加在一起,并且鼠标悬停在卡片区域后,卡片整齐排列。 CSS3 知识点 transform 属性的 rotate 值运用content 属性的 attr 值运用 实现页面整体布局 <div …...
首饰饰品经营商城小程序的作用是什么
首饰如耳钉、戒指、手镯等除了高价值产品外,还有很多低价产品,市场需求客户众多,在实际经营中,商家们也会面临一些痛点。 私域话题越来越多加之线上线下同行竞争、流量匮乏等,更对商家选择自建商城经营平台。 通过【…...

华为OD机试真题【服务器能耗统计】
1、题目描述 【服务器能耗统计】 服务器有三种运行状态:空载、单任务、多任务,每个时间片的能耗的分别为1、3、4; 每个任务由起始时间片和结束时间片定义运行时间; 如果一个时间片只有一个任务需要执行,则服务器处于单任务状志; 如果一个时间片有多个任务需要执行,则服务器处于…...
)
ubuntu按下del却出现空格(命令行下键盘错乱)
问题: 有一天远程我的ubuntu 20.04,发现为何按 del 会产生空格后移的效果,up键也会重叠显示,首先感觉是这个远程软件有问题,于是又换了xshell,发现还是不行,只能打开积灰已久的笔记本࿰…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
