数据结构-优先级队列(堆)
文章目录
目录
文章目录
前言
一 . 堆
二 . 堆的创建(以大根堆为例)
堆的向下调整(重难点)
堆的创建
堆的删除
向上调整
堆的插入
三 . 优先级队列
总结
前言
大家好,今天给大家讲解一下堆这个数据结构和它的实现 - 优先级队列
一 . 堆
堆(Heap)是一种基于完全二叉树的数据结构,具有以下特点:
-
完全二叉树:堆是一种完全二叉树,即除了最后一层外,其他层的节点都是满的,并且最后一层的节点都靠左排列。
-
堆序性:堆中的每个节点都满足堆序性质,即对于最大堆(Max Heap),父节点的值大于或等于其子节点的值;对于最小堆(Min Heap),父节点的值小于或等于其子节点的值。
堆通常用数组来实现,其中数组的索引表示节点在堆中的位置。对于一个节点在索引i的堆,其左子节点在索引2i,右子节点在索引2i+1,父节点在索引i/2。
堆常常被用来实现优先级队列,因为它能够快速找到最大或最小的元素,并且在插入和删除操作时保持堆序性质。
常见的堆有两种类型:
-
最大堆(大根堆):父节点的值大于或等于其子节点的值。最大堆的根节点是堆中的最大元素。
-
最小堆(小根堆):父节点的值小于或等于其子节点的值。最小堆的根节点是堆中的最小元素。
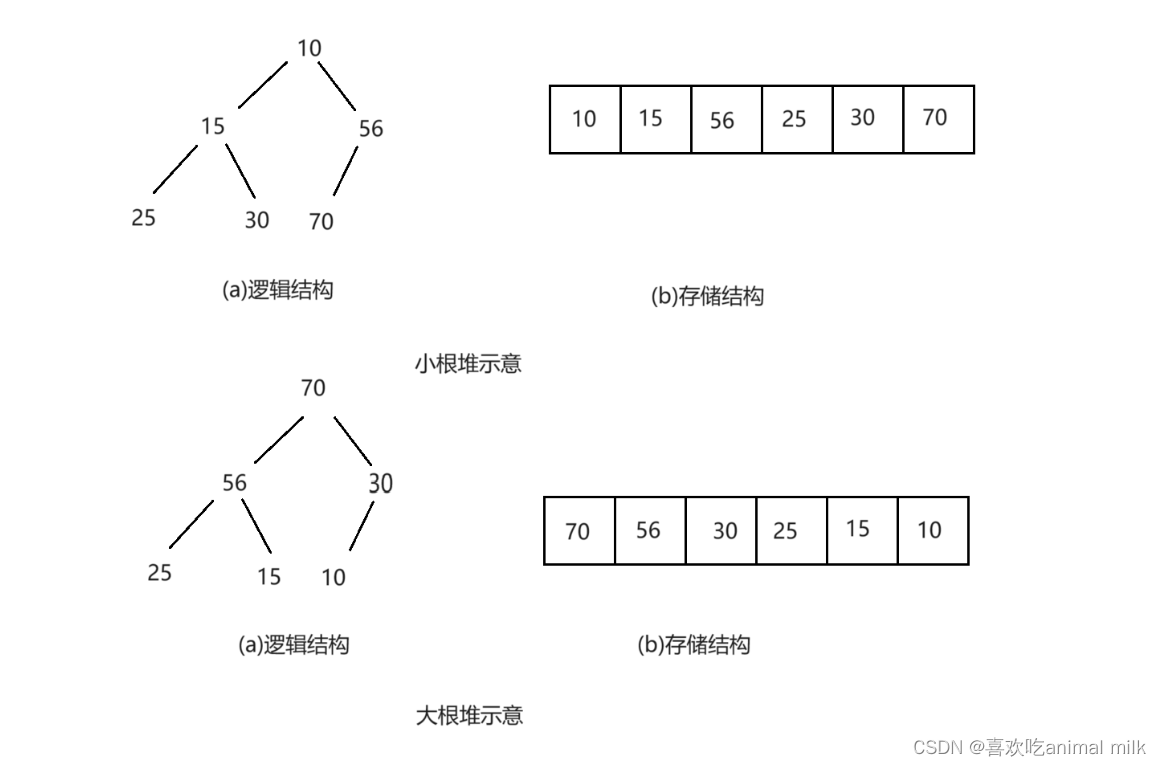
堆的常见操作包括:
-
插入(Insertion):将一个元素插入到堆中,需要保持堆序性质。
-
删除根节点(Delete Root):删除堆中的根节点,需要调整堆以保持堆序性质。
-
查找最大/最小元素(Find Max/Min):在最大堆中查找最大元素,在最小堆中查找最小元素,时间复杂度为O(1)。
-
堆排序(Heap Sort):利用堆的性质进行排序,时间复杂度为O(nlogn)。
二 . 堆的创建(以大根堆为例)
初始化工作
public class BigHeap {int[] elem; // 用来记录堆中的元素int size;public BigHeap(int capacity) {elem = new int[capacity];}//再初始化的时候默认给一个数组public void initHeap(int[] arr) {for (int i = 0; i < arr.length; i++) {elem[i] = arr[i];size++;}}public boolean isFull() {return elem.length == size;}public void swap(int i,int j){int temp = elem[i];elem[i] = elem[j];elem[j] = temp;}}
堆的向下调整(重难点)
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,如果将其创建成大根堆呢?
父节点的值大于或等于其子节点的值。最大堆的根节点是堆中的最大元素。
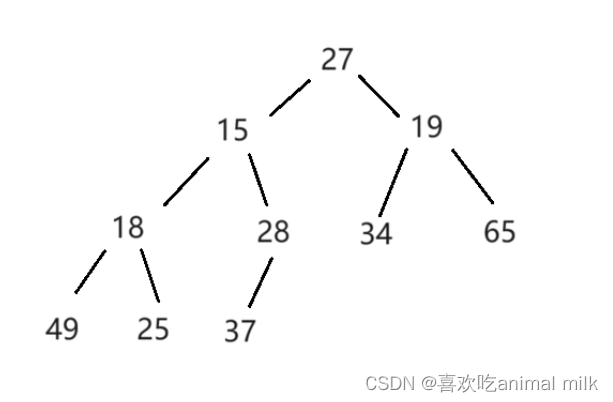
根据层序遍历构建出的二叉树显然并不符合我们的要求,这个是时候我们就需要进行向下调整
在最大堆中,向下调整的过程是将当前节点与其子节点中较大的节点进行比较,如果当前节点小于其中较大的子节点,就将它们交换位置。然后,继续向下比较和交换,直到当前节点不再小于其子节点或者已经到达叶子节点。
思考一下,这个时候我们应该从哪个节点进行调整?
我们通常是从最后一个非叶子节点开始向下调整,直到根节点或者到达叶子节点为止。从最后一个非叶子节点开始向下调整的原因是,只有非叶子节点才有子节点,而叶子节点没有子节点,所以没有必要对叶子节点进行向下调整操作。
最后一个非叶子节点的索引可以通过公式计算得到:n/2-1,其中n是堆中元素的数量。
步骤
1. 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子,因为是完全二叉树)
2. 如果parent的左孩子存在,即:child < len, 进行以下操作,直到parent的左孩子不存在
- parent右孩子是否存在,存在找到左右孩子中最大的孩子,让child进行标记
- 将parent与较大的孩子child比较如果:
- parent小大于较大的孩子child,调整结束
- 否则:交换parent与较大的孩子child,交换完成之后,parent中小的元素向下移动,可能导致子树不满足堆的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续2(上面的)。
图解
{ 27,15,19,18,28,34,65,49,25,37 }
len: 数组的长度
parent: 表示指向需要调整的节点指针
child: 表示指向孩子节点的指针
最后一个非叶子节点: 根据公式parent = (child-1)/2 在这里child表示最后一个节点的索引
parent = (len - 1 - 1)/2 = 4 我们应该从4索引开始进行向下调整
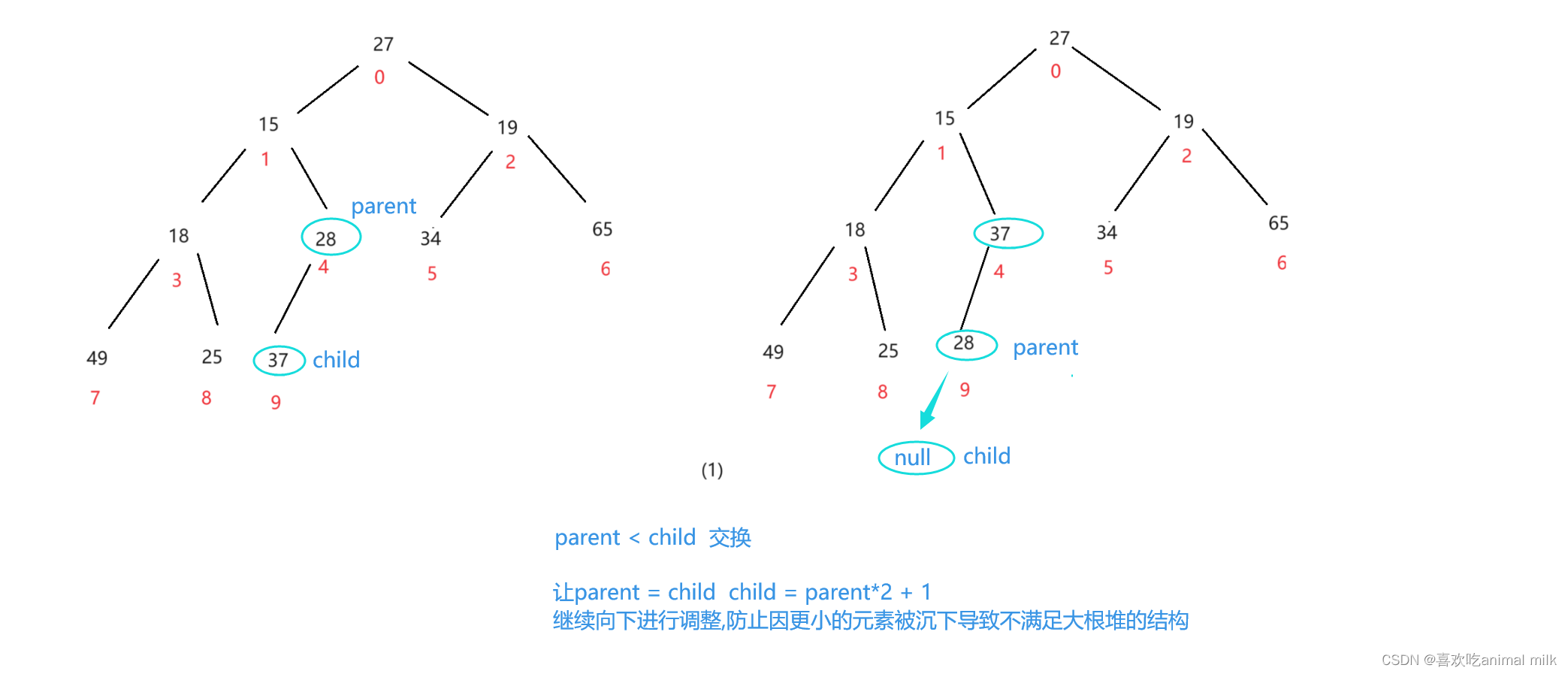

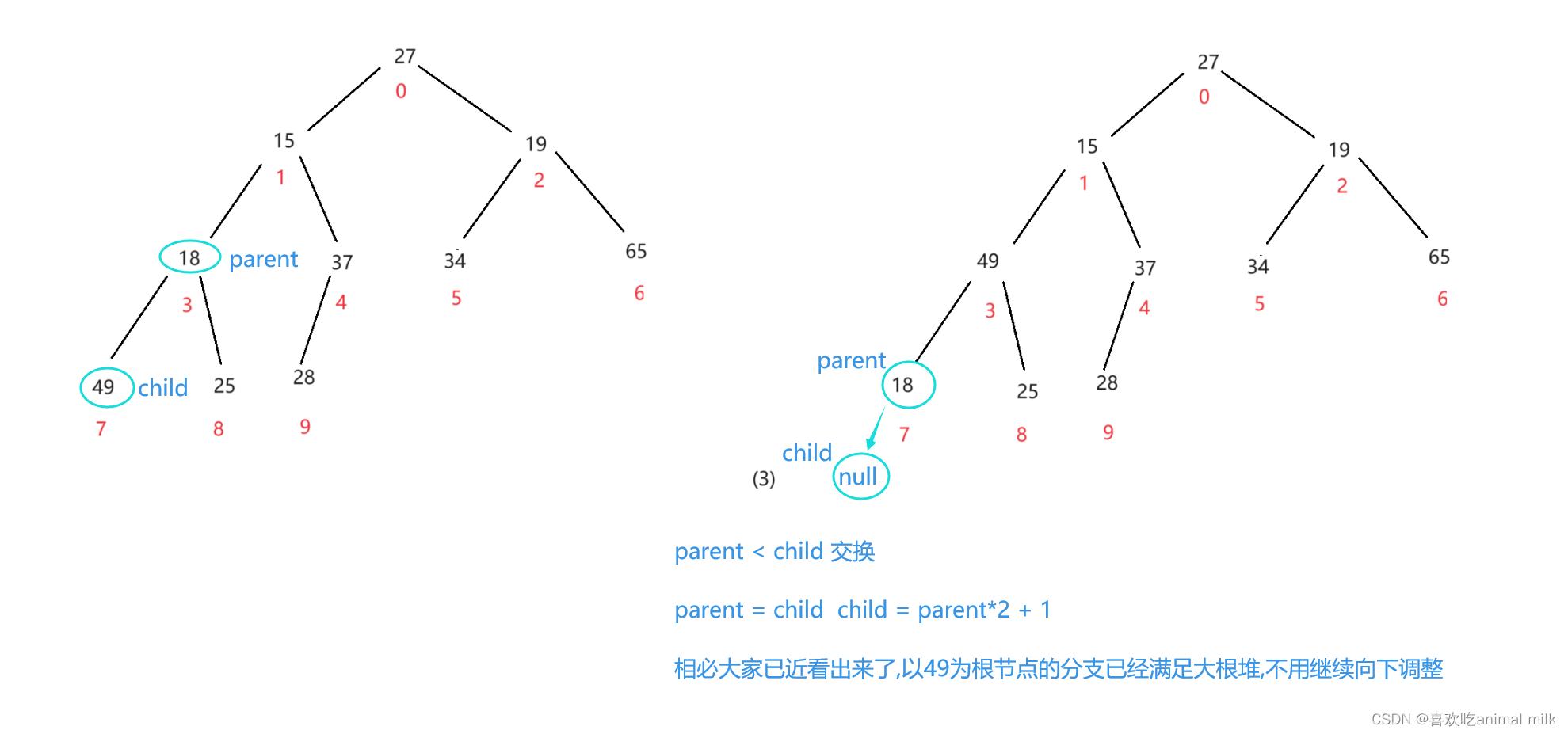
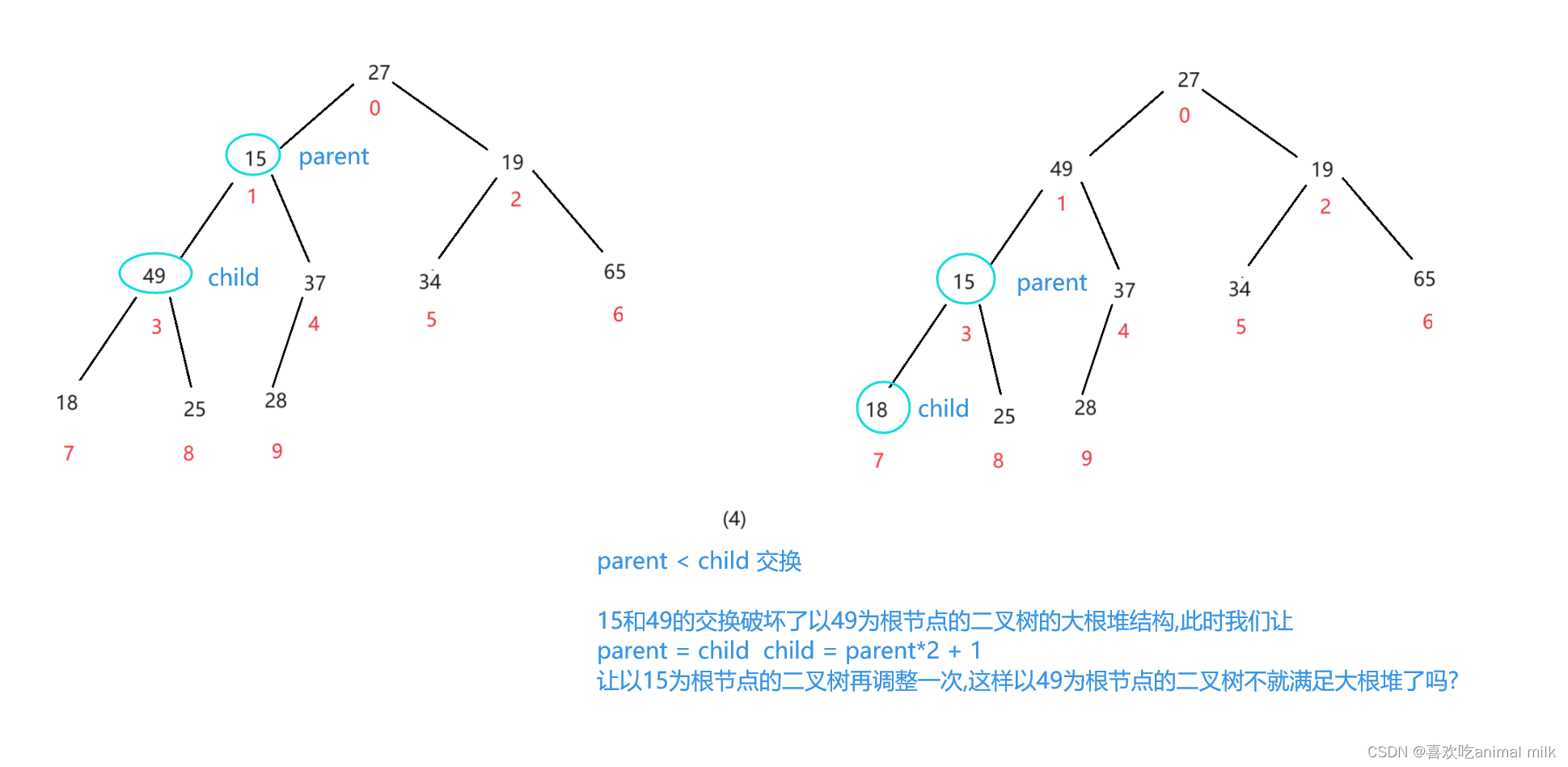
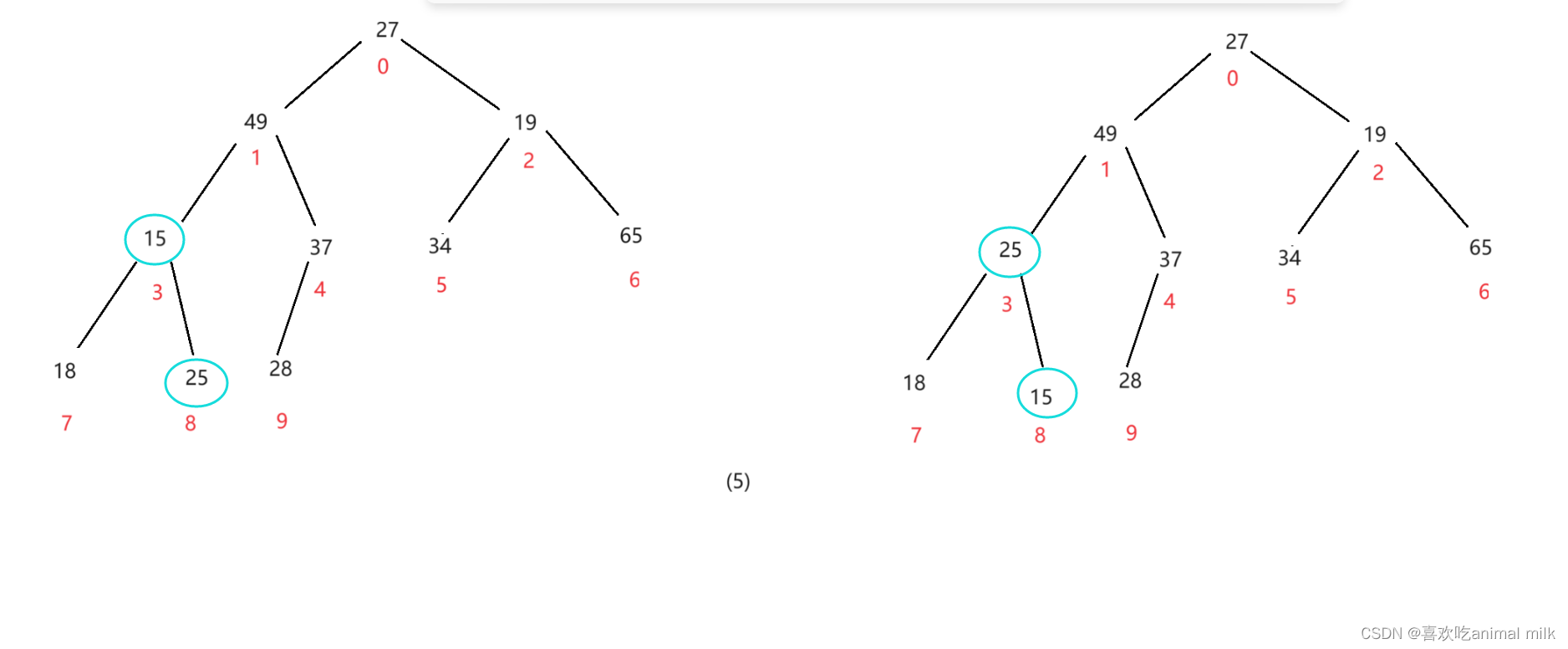
进行到这里左子树宣告调整完毕,开始进行右子树的调整
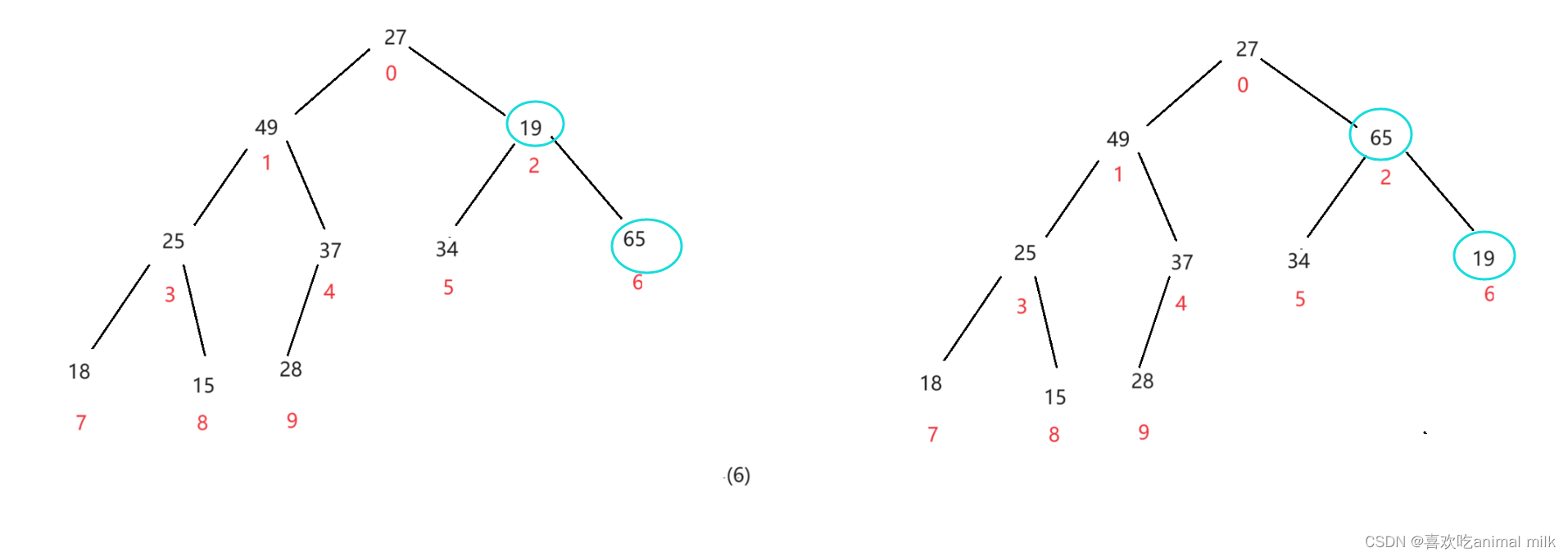
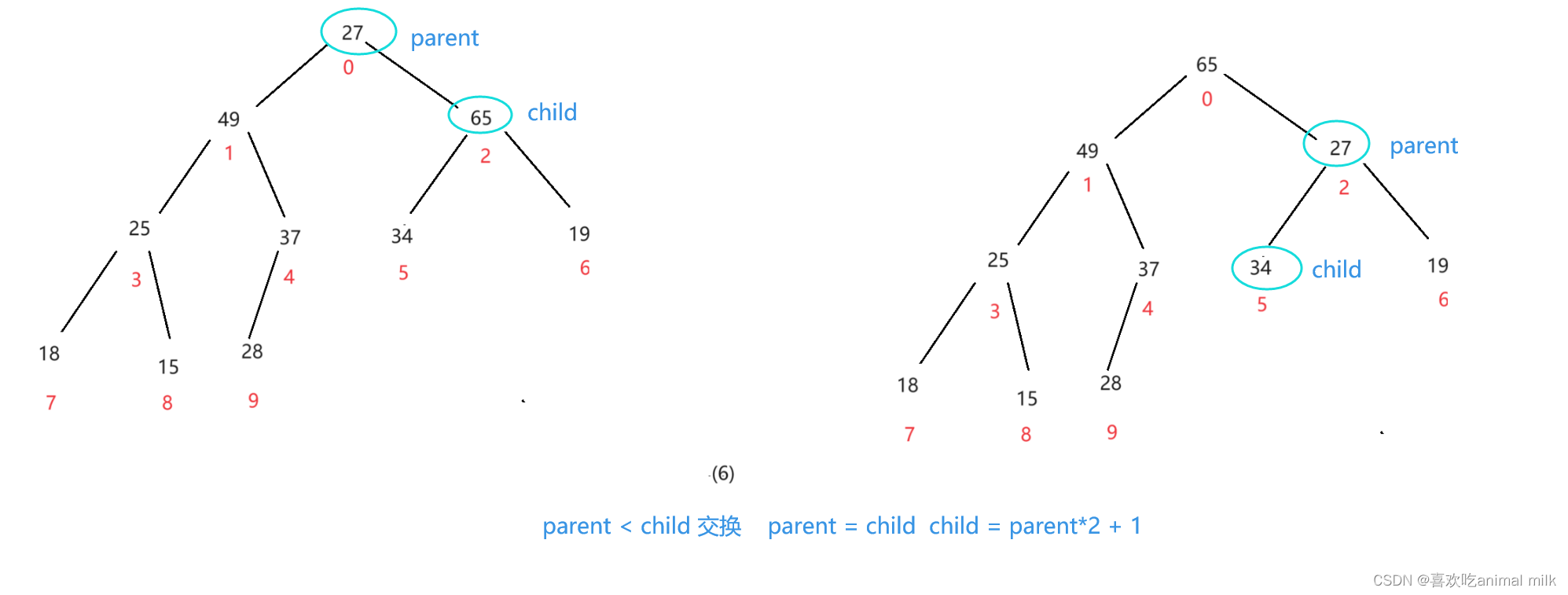
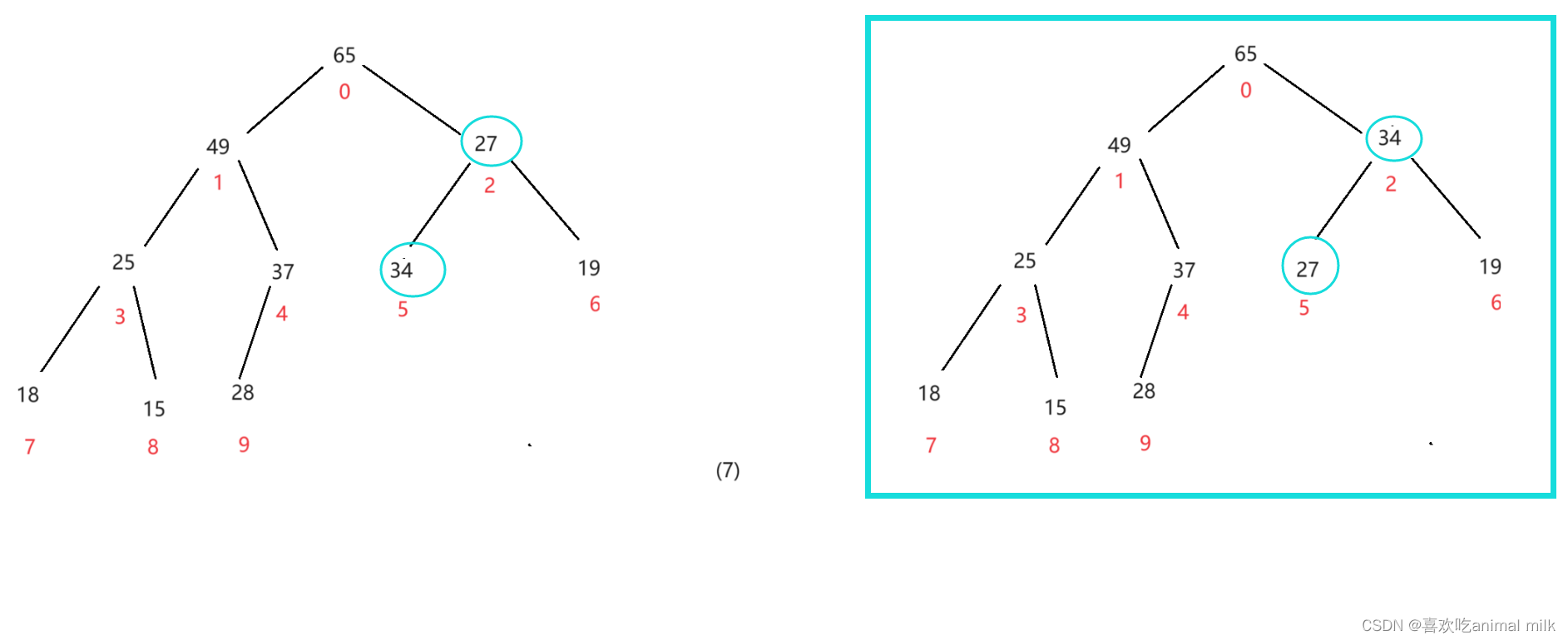 调整完毕!
调整完毕!
代码实现
private void shiftDown(int parent, int len) {int child = 2 * parent + 1;// 对交换引起的堆结构的改变进行调整(如果改变就调整)while (child < len) {// 找出左右孩子中最大的孩子,用child进行记录if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}// 判断大小关系if (elem[child] > elem[parent]) {swap(child,parent);// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整parent = child;child = 2 * parent + 1;} else {// 左孩子为空,表示以最开始的parent为根的二叉树已经是大根堆结构break;}}}堆的创建
public void createHeap() {// 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整for (int parent = (size - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent, size);}}堆的删除
注意:堆的删除一定删除的是堆顶元素。具体如下:
1. 将堆顶元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
3. 对堆顶元素进行向下调整
public int poll(){int temp = elem[0];swap(0, size);size--;// 调整完之后需要进行先下调整,因为原来的最后一个元素变成了堆顶元素,不用想的肯定不满足大根堆的结构shiftDown(0, size);return temp;}向上调整
在最大堆中,向上调整的过程是将当前节点与其父节点进行比较,如果当前节点大于其父节点,就将它们交换位置。然后,继续向上比较和交换,直到当前节点不再大于其父节点或者已经到达根节点。
private void shiftUp(int child) {while (child != 0) {int parent = (child - 1) / 2;if (elem[parent] < elem[child]) {swap(child,parent);child = parent;} else {break;}}}堆的插入
堆的插入总共需要两个步骤:
1. 先将元素放入到底层空间中(注意:空间不够时需要扩容)
2. 将最后新插入的节点向上调整,直到满足堆的性质
小根堆中插入10

public void offer(int val) {if (isFull()) {this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);}elem[size] = val;shiftUp(size);size++;}总代码
public class BigHeap {int[] elem;int size;public BigHeap(int capacity) {elem = new int[capacity];}public void initHeap(int[] arr) {for (int i = 0; i < arr.length; i++) {elem[i] = arr[i];size++;}}public void createHeap() {for (int parent = (size - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent, size);}}public int poll(){int temp = elem[0];swap(0, size);size--;// 调整完之后需要进行先下调整,因为原来的最后一个元素变成了堆顶元素,不用想的肯定不满足大根堆的结构shiftDown(0, size);return temp;}private void shiftDown(int parent, int len) {int child = 2 * parent + 1;// 对交换引起的堆结构的改变进行调整(如果改变就调整)while (child < len) {// 找出左右孩子中最大的孩子,用child进行记录if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}// 判断大小关系if (elem[child] > elem[parent]) {swap(child,parent);// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整parent = child;child = 2 * parent + 1;} else {// 左孩子为空,表示以最开始的parent为根的二叉树已经是大根堆结构break;}}}public void offer(int val) {if (isFull()) {this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);}elem[size] = val;shiftUp(size);size++;}private void shiftUp(int child) {while (child != 0) {int parent = (child - 1) / 2;if (elem[parent] < elem[child]) {swap(child,parent);child = parent;} else {break;}}}public boolean isFull() {return elem.length == size;}public void swap(int i,int j){int temp = elem[i];elem[i] = elem[j];elem[j] = temp;}
}三 . 优先级队列
前面介绍过队列,队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队 列时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适,比如:在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话;初中那会班主任排座位时可能会让成绩好的同学先挑座位。 在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数 据结构就是优先级队列(Priority Queue)。
优先级队列可以用于很多场景,例如任务调度、进程调度、事件处理等。在任务调度中,可以根据任务的优先级来决定先执行哪些任务;在进程调度中,可以根据进程的优先级来决定先执行哪些进程;在事件处理中,可以根据事件的优先级来决定先处理哪些事件。
在实际应用中,优先级队列可以通过使用堆来实现,因为堆具有良好的时间复杂度和空间复杂度。通过使用堆来实现优先级队列,可以在log₂ n的时间复杂度内插入和删除元素,以及在O(1)的时间复杂度内获取优先级最高的元素。
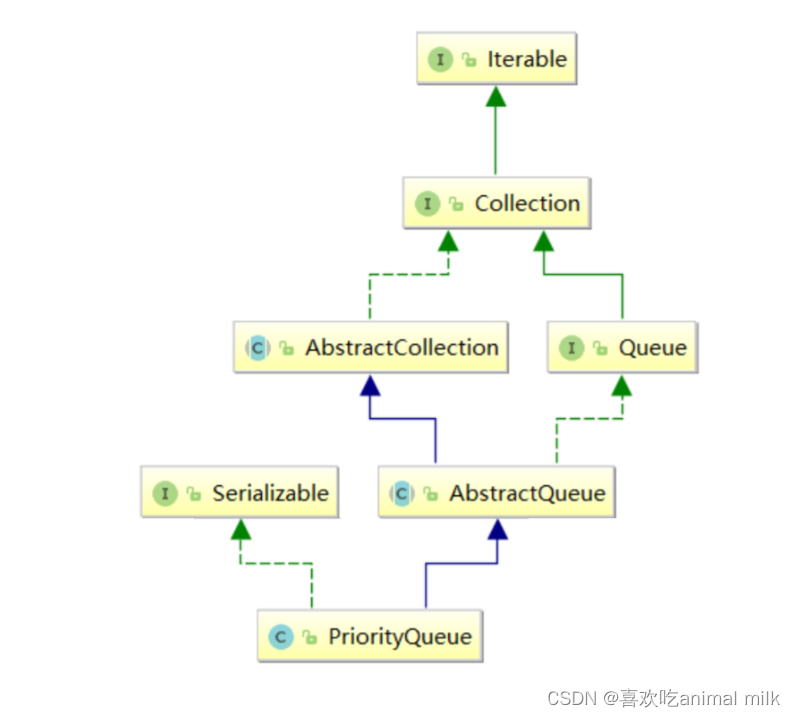
注意点:
1. 使用时必须导入PriorityQueue所在的包
2. PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException异常
3. 不能插入null对象,否则会抛出NullPointerException
4. 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
5. 插入和删除元素的时间复杂度为O(log₂ n)
6. PriorityQueue底层使用了堆数据结构
7. PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素
堆模拟实现优先级队列
class MyPriorityQueue {// 演示作用,不再考虑扩容部分的代码private int[] array = new int[100];private int size = 0;public void offer(int e) {array[size++] = e;shiftUp(size - 1);}public int poll() {int oldValue = array[0];array[0] = array[size--];shiftDown((size-1-1)/2,size);return oldValue;}public int peek() {return array[0];}}总结
这篇文章给大家重点讲解了堆的模拟实现还有其应用之一 优先级队列,大家好好理解,我们下一篇博客见。
相关文章:

数据结构-优先级队列(堆)
文章目录 目录 文章目录 前言 一 . 堆 二 . 堆的创建(以大根堆为例) 堆的向下调整(重难点) 堆的创建 堆的删除 向上调整 堆的插入 三 . 优先级队列 总结 前言 大家好,今天给大家讲解一下堆这个数据结构和它的实现 - 优先级队列 一 . 堆 堆(Heap࿰…...
C++11新特性(语法糖,新容器)
距离C11版本发布已经过去那么多年了,为什么还称为新特性呢?因为笔者前面探讨的内容,除了auto,范围for这些常用的,基本上是用着C98的内容,虽说C11已经发布很多年,却是目前被使用最广泛的版本。因…...
开机可用内存分析Tip
一、开机内存简介 开机内存指的是开机一段时间稳定后的可用内存。一般项目都会挑选同平台其他优秀竞品内存数据,这个也是衡量性能的一个重要标准。所以要进行开机内存检测,同时优化非法内存进程占用。 二、测试前期核查任务 开机内存测试前要进行测试机…...

【Python基础】4. 基本语句
文章目录 注释(Comment)解释伴随行文本编码问题 输入输出语句(Input & Output)输出语句普通输出格式化输出(3种)format 格式总结 输入语句 基本语句if 语句match 语句(Python3.10 新增&…...

兼顾友好与安全,隐私协议 Unijoin 助推新一轮 Web3 浪潮
区块链本身不仅崇尚去中心化,同时也崇尚公开透明,虽然这正在让 DAO 治理等变得更加公平,但它同时也是一把双刃剑,个人交易者尤其是一些巨鲸交易者的所以链上交易都被公之于众,这似乎并不是他们想要的结果。 所以从加密…...
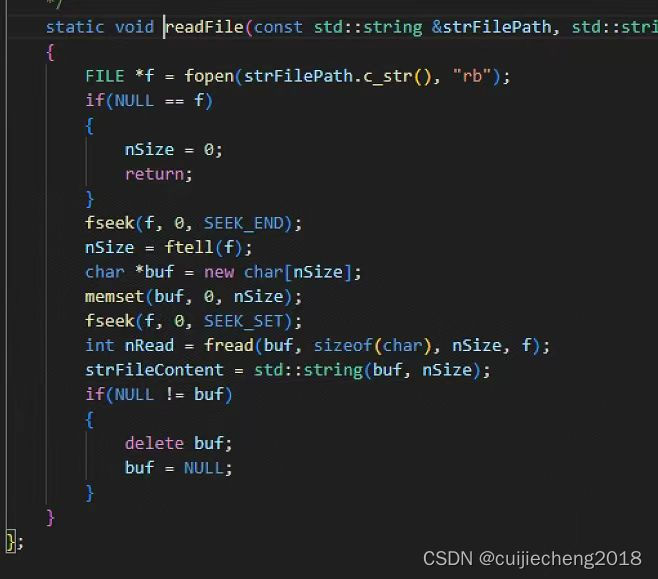
TCP端口崩溃,msg:socket(): Too many open files
一、现象 linux系统中运行了一个TCP服务器,该服务器监听的TCP端口为10000。但是长时间运行时发现该端口会崩溃,TCP客户端连接该端口会失败: 可以看到进行三次握手时,TCP客户端向该TCP服务器的10000端口发送了SYN报文,…...
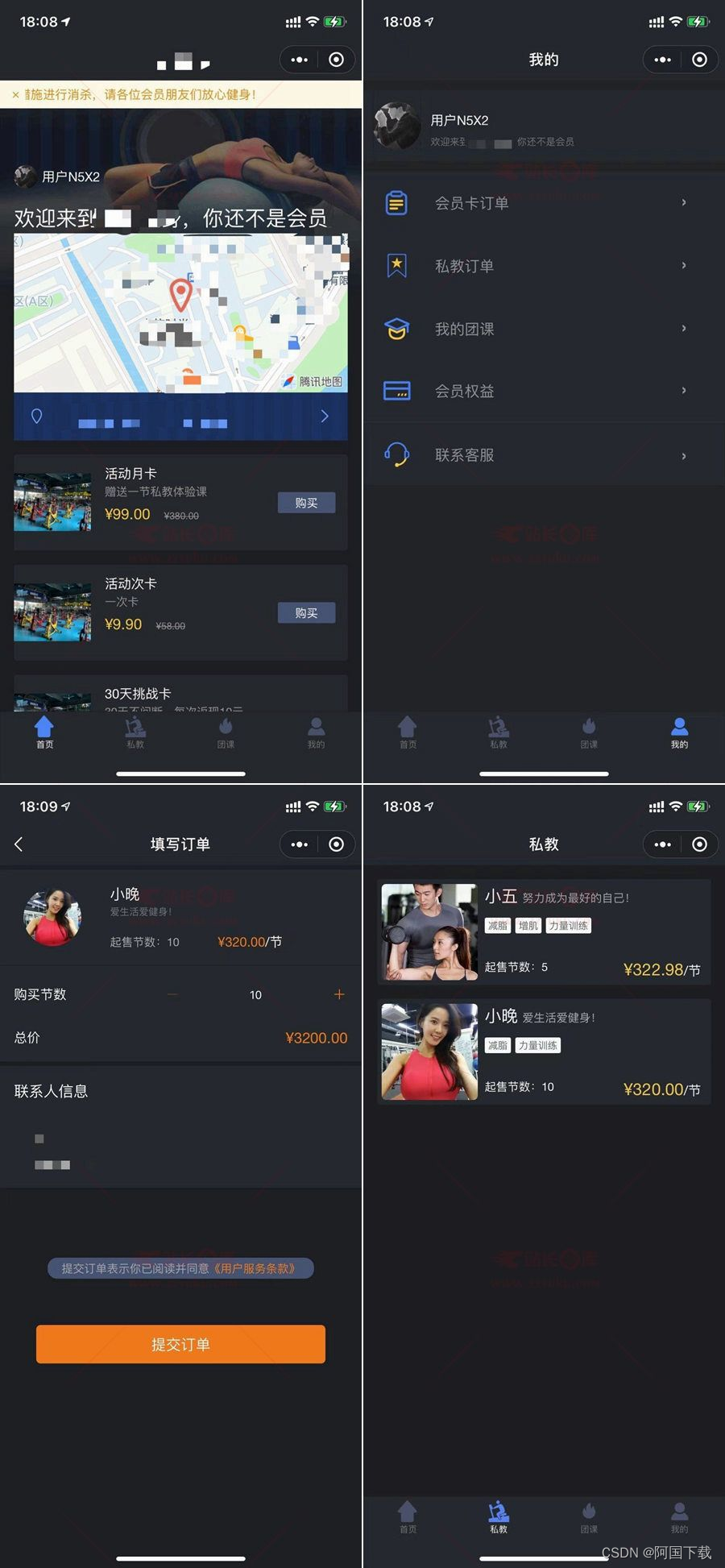
基于Laravel 5.6的运动健身类小程序前后端源码
基于Laravel 5.6的运动健身、健康类小程序前后端源码,一套比较基础的运动健康、健身类小程序源码。朋友自己无聊写的,比较基础,有需要的可以拿去修修改改升级开发一下。 使用宝塔安装,比较省事,PHP相关的扩展需要启用…...
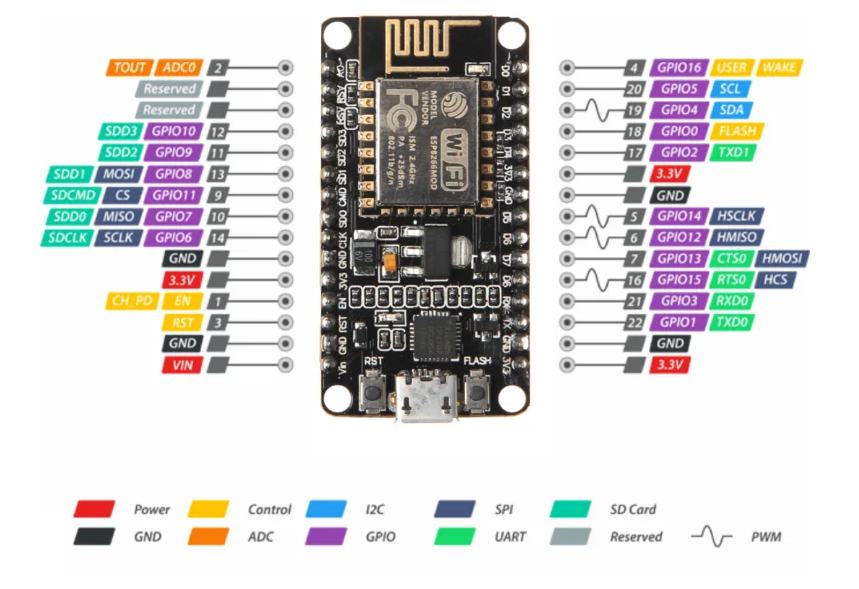
NodeMCU ESP8266硬件开发板的熟悉
文章目录 硬件开发环境的熟悉基础介绍什么是 ESP8266 NodeMCU?NodeMCU芯片ESP12-E 模组开发板 ESP8266 版本引脚图Power GND I2CGPIOADCUARTSPIPWMControl 总结 硬件开发环境的熟悉 基础介绍 什么是 ESP8266 NodeMCU? ESP8266是乐鑫开发的一款低成本 …...
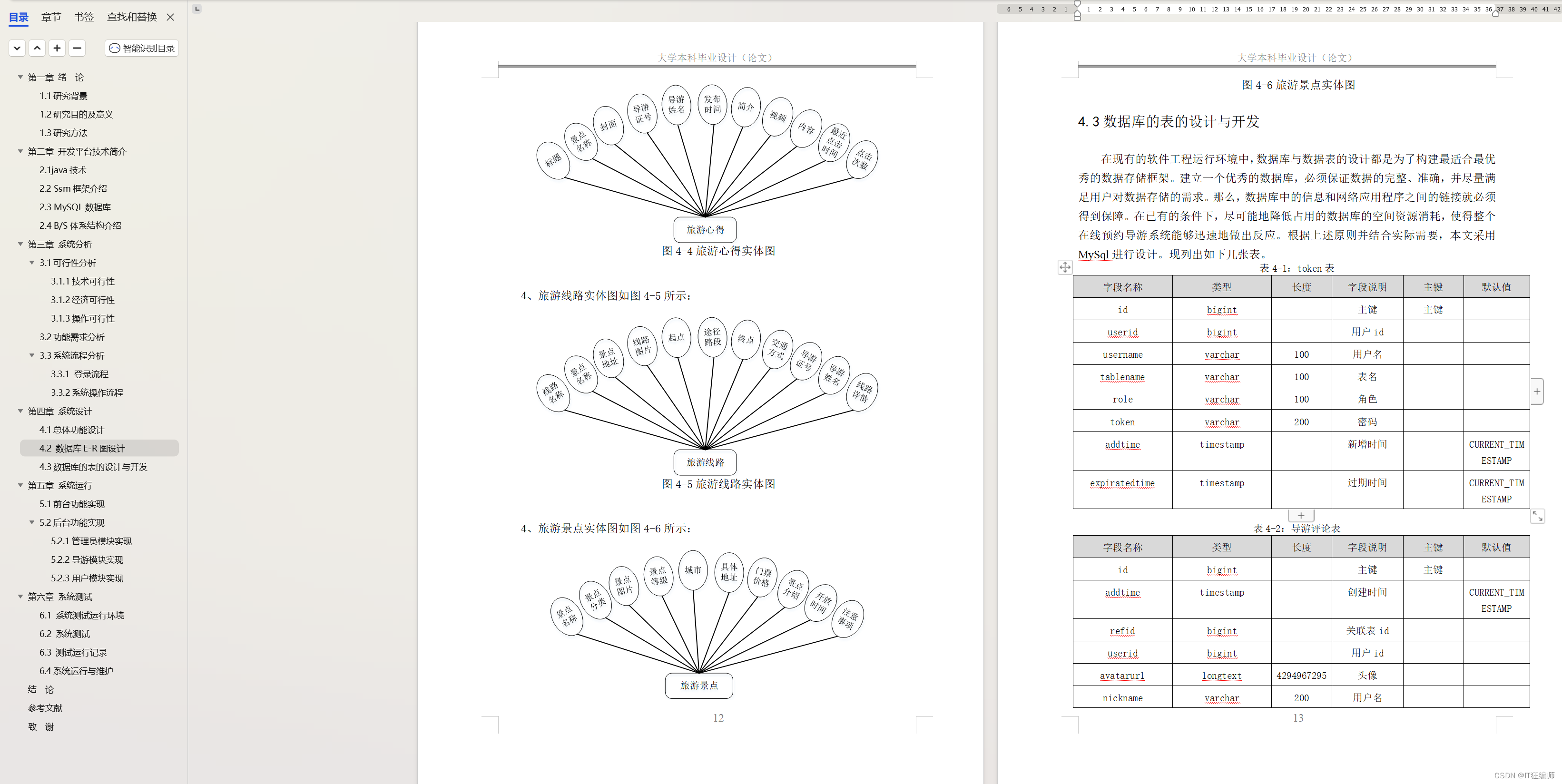
计算机毕业设计 基于SSM的在线预约导游系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
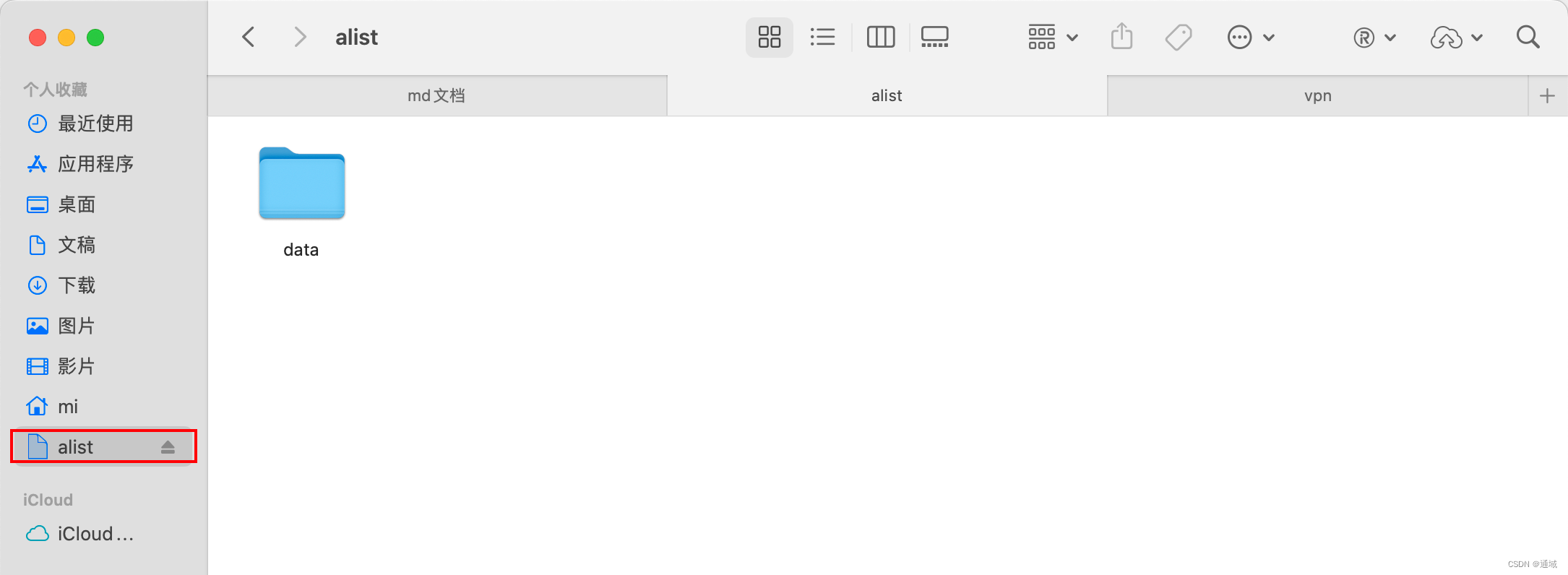
Mac 挂载 Alist网盘
挂载服务器的Alist 网盘到 Mac mac,使用的是 CloundMounter 这个软件进行挂载 http://ip:port/dav/ 需要在末尾加上 /dav/ 在一些服务器上,为了提供WebDAV服务,需要在URL地址的末尾添加"/dav/“。这是因为WebDAV协议规定了一些标准的URL路径&#x…...
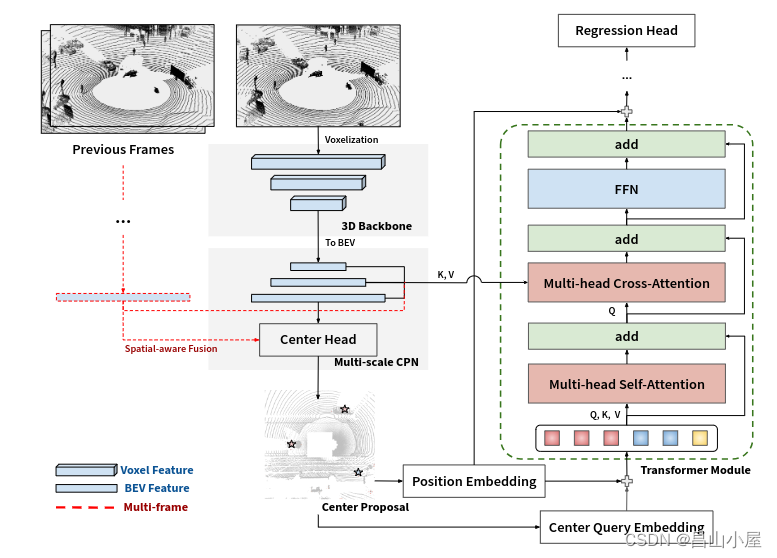
【多模态融合】TransFusion学习笔记(1)
工作上主要还是以纯lidar的算法开发,部署以及系统架构设计为主。对于多模态融合(这里主要是只指Lidar和Camer的融合)这方面研究甚少。最近借助和朋友们讨论论文的契机接触了一下这方面的知识,起步是晚了一点,但好歹是开了个头。下面就借助TransFusion论文…...

(二)正点原子STM32MP135移植——TF-A移植
目录 一、TF-A概述 二、编译官方代码 2.1 解压源码 2.2 打补丁 2.3 编译准备 (1)修改Makfile.sdk (2)设置环境变量 (3)编译 三、移植 3.1 复制官方文件 3.2 修改电源 3.3 修改TF卡和emmc 3.4 添…...
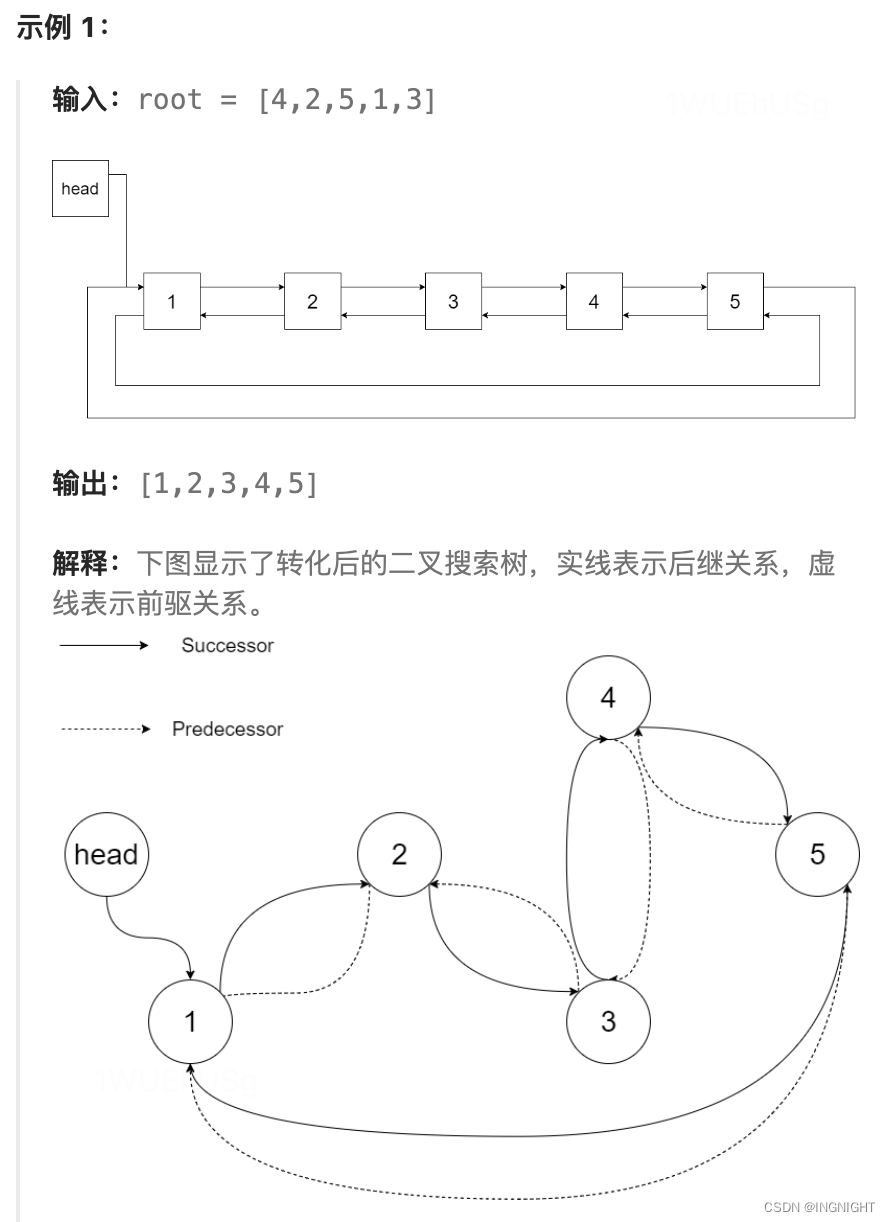
将二叉搜索树转化为排序的双向链表
链接: LCR 155. 将二叉搜索树转化为排序的双向链表 题解: /* // Definition for a Node. class Node { public:int val;Node* left;Node* right;Node() {}Node(int _val) {val _val;left NULL;right NULL;}Node(int _val, Node* _left…...
电脑dll丢失应该怎么解决,dll文件丢失怎么恢复方法分享
DLL(Dynamic Link Library,动态链接库)是一种可执行文件,它包含了在程序运行时需要调用的代码和资源。DLL 文件的主要作用是实现代码和资源的共享,这样在多个程序之间就可以避免重复的代码和资源,从而节省系…...

通达信和同花顺能否实现程序化自动交易股票,量化交易如何实现?
以下写给正在寻找自动交易接口的朋友,首先,不是那种设置个简单条件的条件单,或者某些客户端上形同鸡肋的策略交易,那些策略根本称不上策略,还有各种限制,不支持这个不支持那个,可设置的参数也不…...
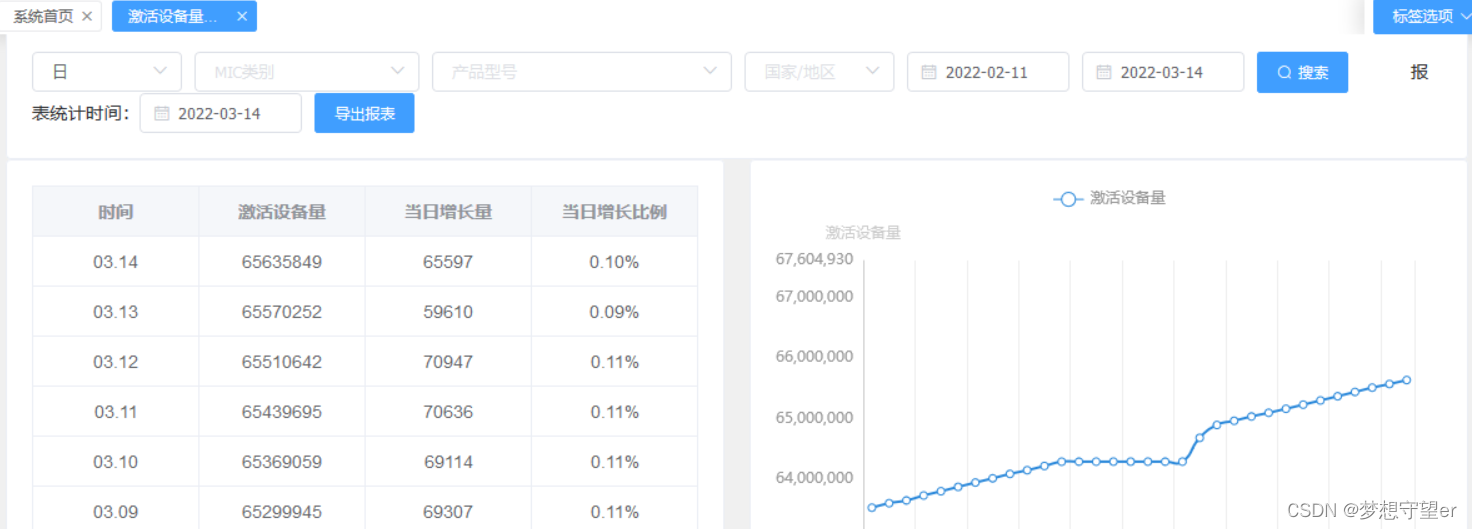
基于Kylin的数据统计分析平台架构设计与实现
目录 1 前言 2 关键模块 2.1 数据仓库的搭建 2.2 ETL 2.3 Kylin数据分析系统 2.4 数据可视化系统 2.5 报表模块 3 最终成果 4 遇到问题 1 前言 这是在TP-LINK公司云平台部门做的一个项目,总体包括云上数据统计平台的架构设计和组件开发,在此只做…...

Linux CentOS7 vim寄存器
计算机中通常所说的寄存器Register一般指的是CPU中的寄存器,用来暂存CPU处理所需要的指令、数据等。 vim中同样也有寄存器,使用的方式和CPU非常类似。 vim中的寄存器(register)作用和windows中的剪切板类似,不过vim中的寄存器不止一个&…...
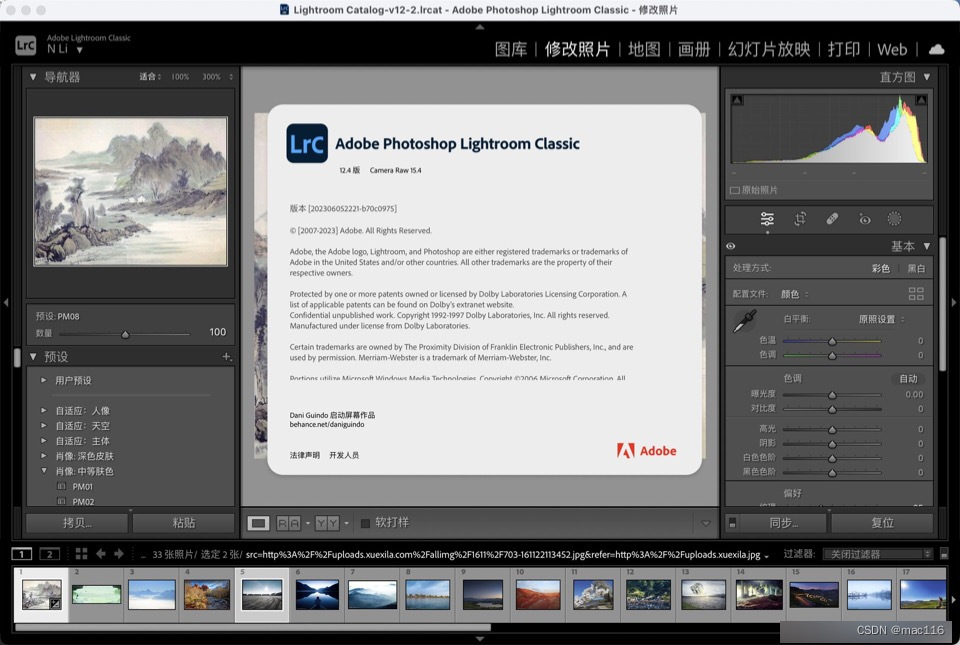
摄影后期图像编辑软件Lightroom Classic 2023 mac中文特点介绍
Lightroom Classic 2023 mac是一款图像处理软件,是数字摄影后期制作的重要工具之一,lrc2023 mac适合数字摄影后期制作、摄影师、设计师等专业人士使用。 Lightroom Classic 2023 mac软件特点 高效的图像管理:Lightroom Classic提供了强大的图…...
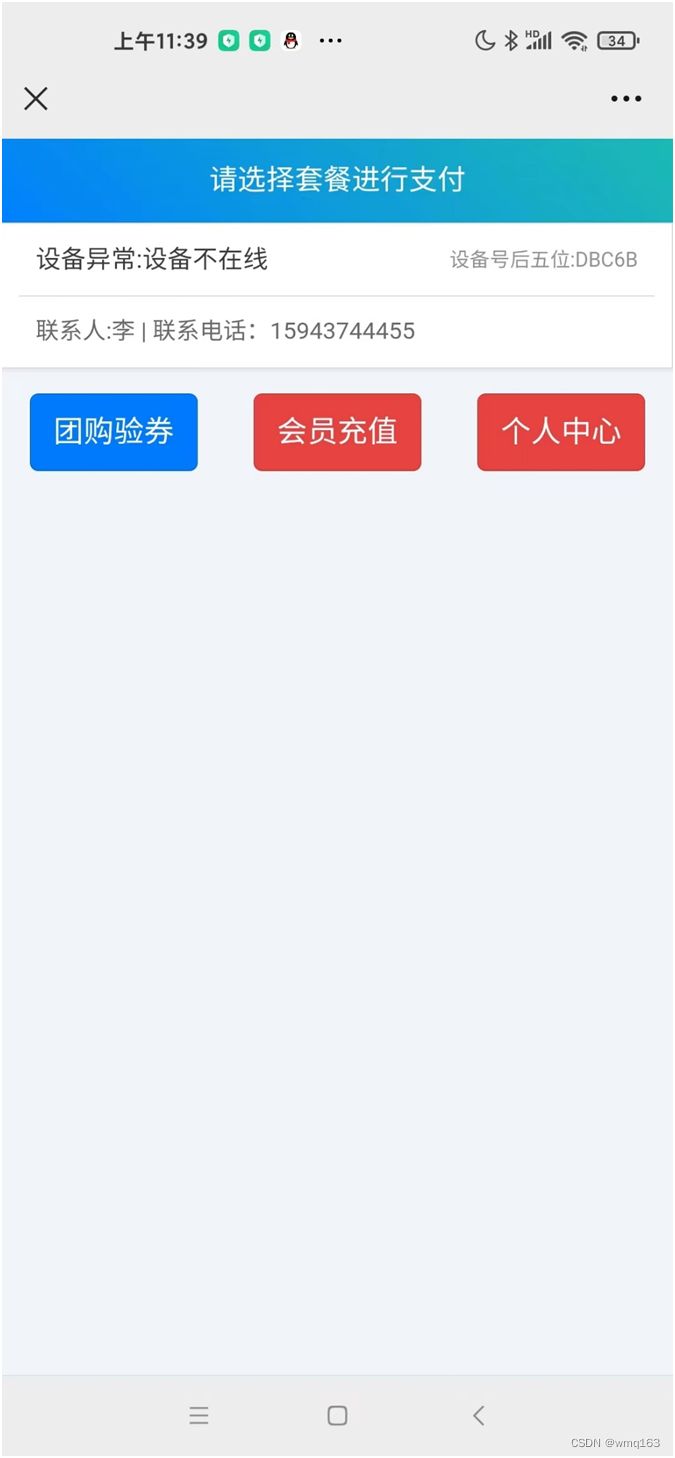
一种4g扫码付费通电控制器方案
之前开发了一款扫码付款通电控制器 功能:用户扫码付款后设备通电,开始倒计时,倒计时结束后设备断电,资金到账商家的商家助手里面,腾讯会收取千分之6手续费。 产品主要应用场景 本产品主要应用于各类无人值守或者自助…...

桌面自动化工具总结
引言:产品经理提出桌面程序需要自动化的测试,避免繁琐的人肉点击。说干就干。 现有自动化工具是五花八门,我找了两个框架。 这两个框架都是基于微软的UIA 框架,链接地址 https://learn.microsoft.com/en-us/windows/win32/winauto/uiauto-providerportal?source=recommen…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
