力扣第226翻转二叉数 c++三种方法 +注释
题目
226. 翻转二叉树
简单
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
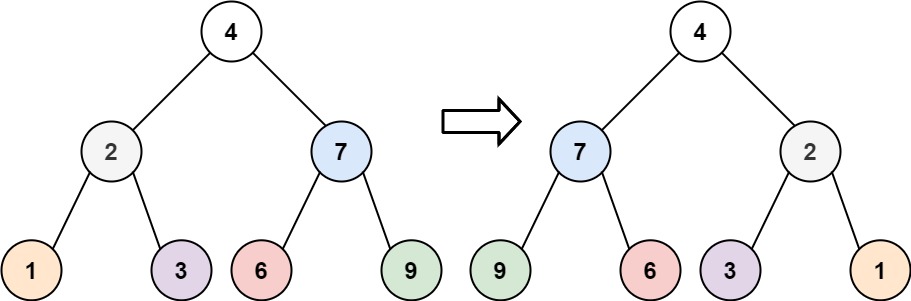
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:
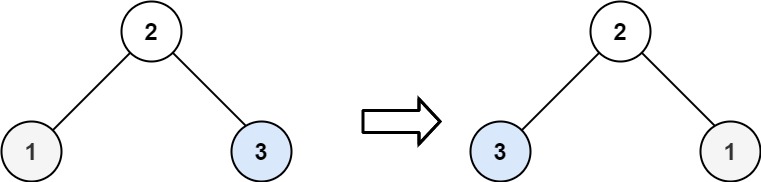
输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
c++ 代码一 (递归法)
class Solution { public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root; // 如果根节点为空,直接返回该节点,不进行翻转操作swap(root->left, root->right); // 交换当前节点的左右子树,实现翻转操作invertTree(root->left); // 递归地对当前节点的左子树进行翻转invertTree(root->right); // 递归地对当前节点的右子树进行翻转return root; // 返回翻转后的根节点} };以上是代码中的注释,解释了每一行代码的作用。
- 如果根节点为空,直接返回根节点,不进行翻转操作。
- 交换当前节点的左右子树,实现翻转操作。
- 递归地对当前节点的左子树进行翻转。
- 递归地对当前节点的右子树进行翻转。
- 返回翻转后的根节点。
c++ 代码二 (迭代法(前序遍历))
class Solution { public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root; // 如果根节点为空,直接返回该节点,不进行翻转操作stack<TreeNode*> st; // 创建一个栈,用于存储待翻转的节点st.push(root); // 将根节点入栈while (!st.empty()) {TreeNode* node = st.top(); // 取出栈顶节点作为当前节点st.pop();swap(node->left, node->right); // 交换当前节点的左右子树,实现翻转操作if (node->right) st.push(node->right); // 如果当前节点的右子树不为空,则将右子树节点入栈,准备进行翻转操作if (node->left) st.push(node->left); // 如果当前节点的左子树不为空,则将左子树节点入栈,准备进行翻转操作}return root; // 返回翻转后的根节点} };以上是代码中的注释,解释了每一行代码的作用。
- 如果根节点为空,直接返回根节点,不进行翻转操作。
- 创建一个栈,用于存储待翻转的节点。
- 将根节点入栈。
- 使用迭代法进行翻转操作:
- 取出栈顶节点作为当前节点。
- 交换当前节点的左右子树,实现翻转操作。
- 如果当前节点的右子树不为空,则将右子树节点入栈,准备进行翻转操作。
- 如果当前节点的左子树不为空,则将左子树节点入栈,准备进行翻转操作。
- 返回翻转后的根节点。
c++ 代码三 (广度优先遍历)
class Solution { public:TreeNode* invertTree(TreeNode* root) {queue<TreeNode*> que; // 创建一个队列,用于存储待翻转的节点if (root != NULL) que.push(root); // 如果根节点不为空,则将根节点入队列while (!que.empty()) { // 当队列不为空时循环执行操作int size = que.size(); // 获取当前队列的大小,即当前层的节点数for (int i = 0; i < size; i++) { // 遍历当前层的节点TreeNode* node = que.front(); // 取出队首节点作为当前节点que.pop(); // 出队列swap(node->left, node->right); // 交换当前节点的左右子树,实现翻转操作if (node->left) que.push(node->left); // 如果当前节点的左子树不为空,则将左子树节点入队列,准备进行翻转操作if (node->right) que.push(node->right); // 如果当前节点的右子树不为空,则将右子树节点入队列,准备进行翻转操作}}return root; // 返回翻转后的根节点} };以上是代码中的注释,解释了每一行代码的作用。
- 创建一个队列,用于存储待翻转的节点。
- 如果根节点不为空,则将根节点入队列。
- 使用迭代法进行翻转操作:
- 获取当前队列的大小,即当前层的节点数。
- 遍历当前层的节点:
- 取出队首节点作为当前节点。
- 交换当前节点的左右子树,实现翻转操作。
- 如果当前节点的左子树不为空,则将左子树节点入队列,准备进行翻转操作。
- 如果当前节点的右子树不为空,则将右子树节点入队列,准备进行翻转操作。
- 返回翻转后的根节点。
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第226翻转二叉数 c++三种方法 +注释
题目 226. 翻转二叉树 简单 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 1: 输入:root [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]示例 2: 输入:root [2,1,3] 输出&am…...
React项目部署 - Nginx配置
写在前面:博主是一只经过实战开发历练后投身培训事业的“小山猪”,昵称取自动画片《狮子王》中的“彭彭”,总是以乐观、积极的心态对待周边的事物。本人的技术路线从Java全栈工程师一路奔向大数据开发、数据挖掘领域,如今终有小成…...
【Vue3】定义全局变量和全局函数
// main.ts import { createApp } from vue import App from ./App.vue const app createApp(App)// 解决 ts 报错 type Filter {format<T>(str: T): string } declare module vue {export interface ComponentCustomProperties {$filters: Filter,$myArgs: string} }a…...

【Pandas】Apply自定义行数
文章目录 1. Series的apply方法2. DataFrame的apply方法2.1 针对列使用apply2.2 针对行使用apply Pandas提供了很多数据处理的API,但当提供的API不能满足需求的时候,需要自己编写数据处理函数, 这个时候可以使用apply函数apply函数可以接收一个自定义函数, 可以将DataFrame的行…...

C#,数值计算——完全VEGAS编码的蒙特·卡洛计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// Complete VEGAS Code /// adaptive/recursive Monte Carlo /// </summary> public abstract class VEGAS { const int NDMX 50; const int …...

纯css实现3D鼠标跟随倾斜
老规矩先上图 为什么今天会想起来整这个呢?这是因为和我朋友吵架, 就是关于这个效果的,就是这个 卡片懸停毛玻璃效果, 我朋友认为纯css也能写, 我则坦言他就是在放狗屁,这种跟随鼠标的3D效果要怎么可能能用纯css写, 然后吵着吵着发现,欸,好像真能用css写哦,我以前还写过这种…...

Pandas数据结构
文章目录 1. Series数据结构1.1 Series数据类型创建1.2 Series的常用属性valuesindex/keys()shapeTloc/iloc 1.3 Series的常用方法mean()max()/min()var()/std()value_counts()describe() 1.4 Series运算加/减法乘法 2. DataFrame数据结构2.1 DataFrame数据类型创建2.2 布尔索引…...

systemverilog function的一点小case
关于function的应用无论是在systemverilog还是verilog中都有很广泛的应用,但是一直有一个模糊的概念困扰着我,今天刚好有时间来搞清楚并记录下来。 关于fucntion的返回值的问题: function integer clog2( input logic[255:0] value);for(cl…...

微服务的初步使用
环境说明 jdk1.8 maven3.6.3 mysql8 idea2022 spring cloud2022.0.8 微服务案例的搭建 新建父工程 打开IDEA,File->New ->Project,填写Name(工程名称)和Location(工程存储位置),选…...
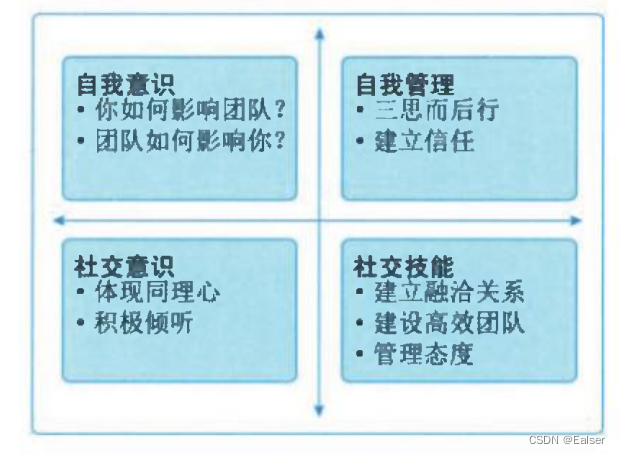
【2023年11月第四版教材】第18章《项目绩效域》(合集篇)
第18章《项目绩效域》(合集篇) 1 章节内容2 干系人绩效域2.1 绩效要点2.2 执行效果检查2.3 与其他绩效域的相互作用 3 团队绩效域3.1 绩效要点3.2 与其他绩效域的相互作用3.3 执行效果检查3.4 开发方法和生命周期绩效域 4 绩效要点4.1 与其他绩效域的相互…...

Android 11.0 mt6771新增分区功能实现三
1.前言 在11.0的系统开发中,在对某些特殊模块中关于数据的存储方面等需要新增分区来保存, 所以就需要在系统分区新增分区,接下来就来实现这个功能,看系列三的实现过程 2.mt6771新增分区功能实现三的核心类 build/make/tools/releasetools/common.py device/mediatek/mt6…...
计算机网络——计算机网络的性能指标(上)-速率、带宽、吞吐量、时延
目录 速率 比特 速率 例1 带宽 带宽在模拟信号系统中的意义 带宽在计算机网络中的意义 吞吐量 时延 发送时延 传播时延 处理时延 例2 例3 速率 了解速率之前,先详细了解一下比特: 比特 计算机中数据量的单位,也是信息论中信…...
)
每日一题 518零钱兑换2(完全背包)
题目 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整…...
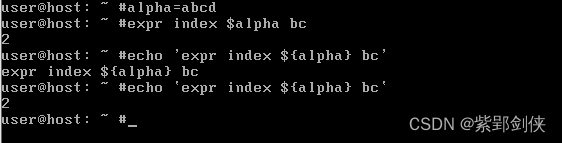
Linux shell编程学习笔记8:使用字符串
一、前言 字符串是大多数编程语言中最常用最有用的数据类型,这在Linux shell编程中也不例外。 本文讨论了Linux Shell编程中的字符串的三种定义方式的差别,以及字符串拼接、取字符串长度、提取字符串、查找子字符串等常用字符串操作,,以及反…...
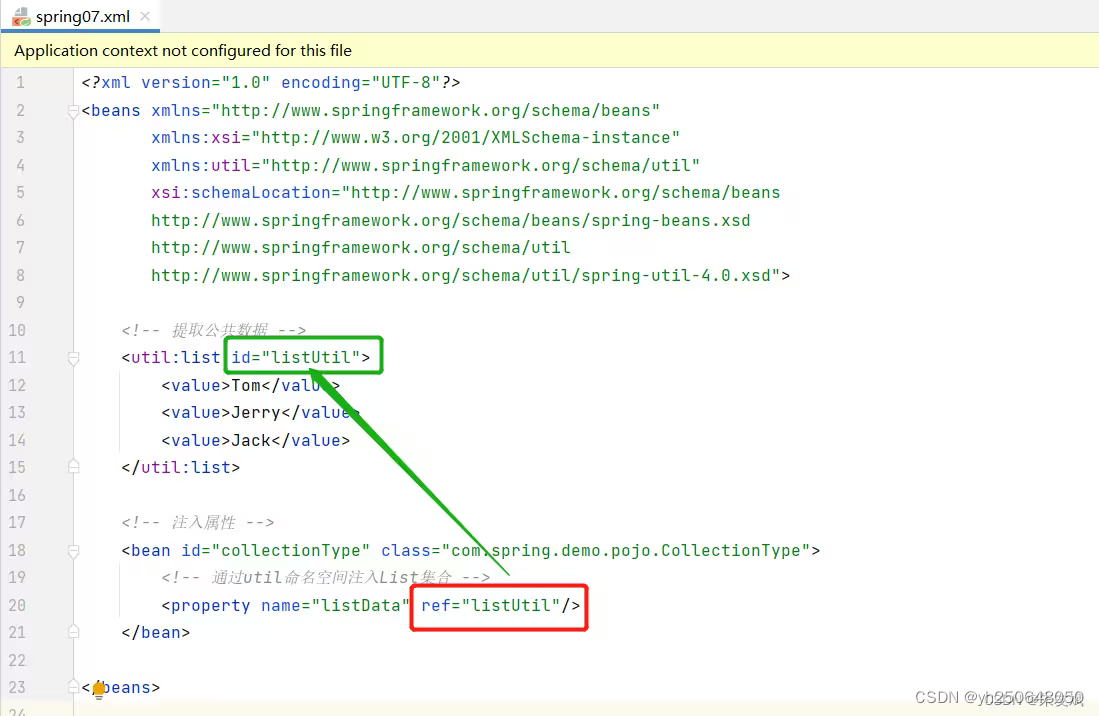
【Spring笔记03】Spring依赖注入各种数据类型
这篇文章,详细介绍一下Spring框架中如何注入各种数据类型,包含:注入基本数据类型、数组、集合、Map映射、Property属性、注入空字符串、注入null值、注入特殊字符等内容,以及如何使用命名空间进行依赖注入。 目录 一、注入各种数据…...

2023计算机保研——双非上岸酒吧舞
我大概是从22年10月份开始写博客的,当时因为本校专业的培养方案的原因,课程很多,有些知识纸质记录很不方便,于是选择了打破了自己的成见使用博客来记录学习生活。对于我个人而言,保研生活在前一大半过程中都比较艰难&a…...
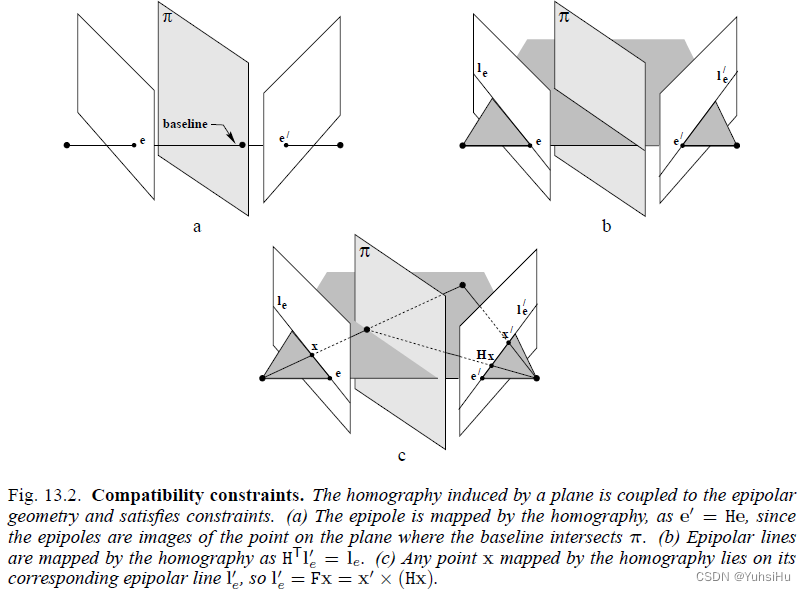
《计算机视觉中的多视图几何》笔记(13)
13 Scene planes and homographies 本章主要讲述两个摄像机和一个世界平面之间的射影几何关系。 我们假设空间有一平面 π \pi π,平面上的一点为 x π x_{\pi} xπ。 x π x_{\pi} xπ分别在两幅图像 P , P ′ P, P P,P′上形成了 x , x ′ x, x x,x′。 那…...
H5移动端购物商城系统源码 小型商城全新简洁风格全新UI 支持易支付接口
一款比较简单的 H5 移动端购物商城系统源码,比较适合单品商城、小型商城使用。带有易支付接口。 源码下载:https://download.csdn.net/download/m0_66047725/88391704 源码下载2:评论留言或私信留言...
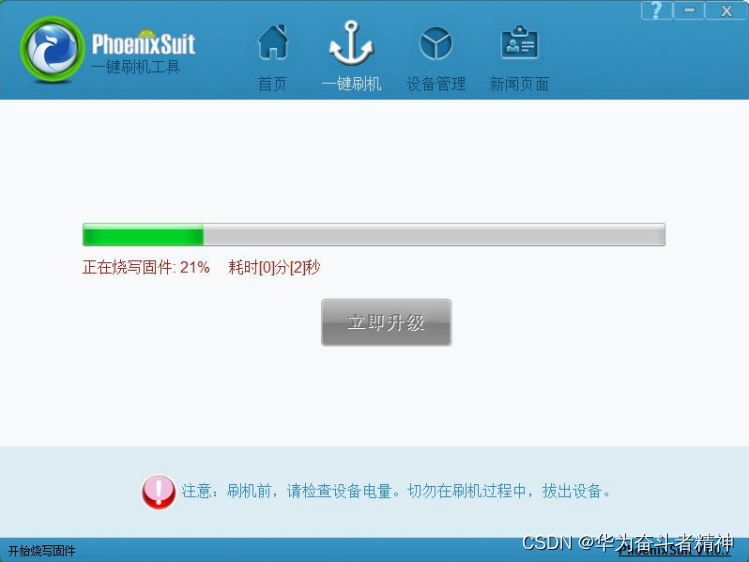
全志ARM926 Melis2.0系统的开发指引⑤
全志ARM926 Melis2.0系统的开发指引⑤ 编写目的8. 固件修改工具(ImageModify)使用8.1.界面说明8.2.操作步骤8.2.1. 配置平台8.2.2. 选择固件8.2.3. 选择要替换的文件8.2.4. 替换文件8.2.5. 保存固件 8.3.注意事项8.4.增加固件修改权限设置8.4.1. 概述8.4.2. 操作说明8.4.2.1.打…...
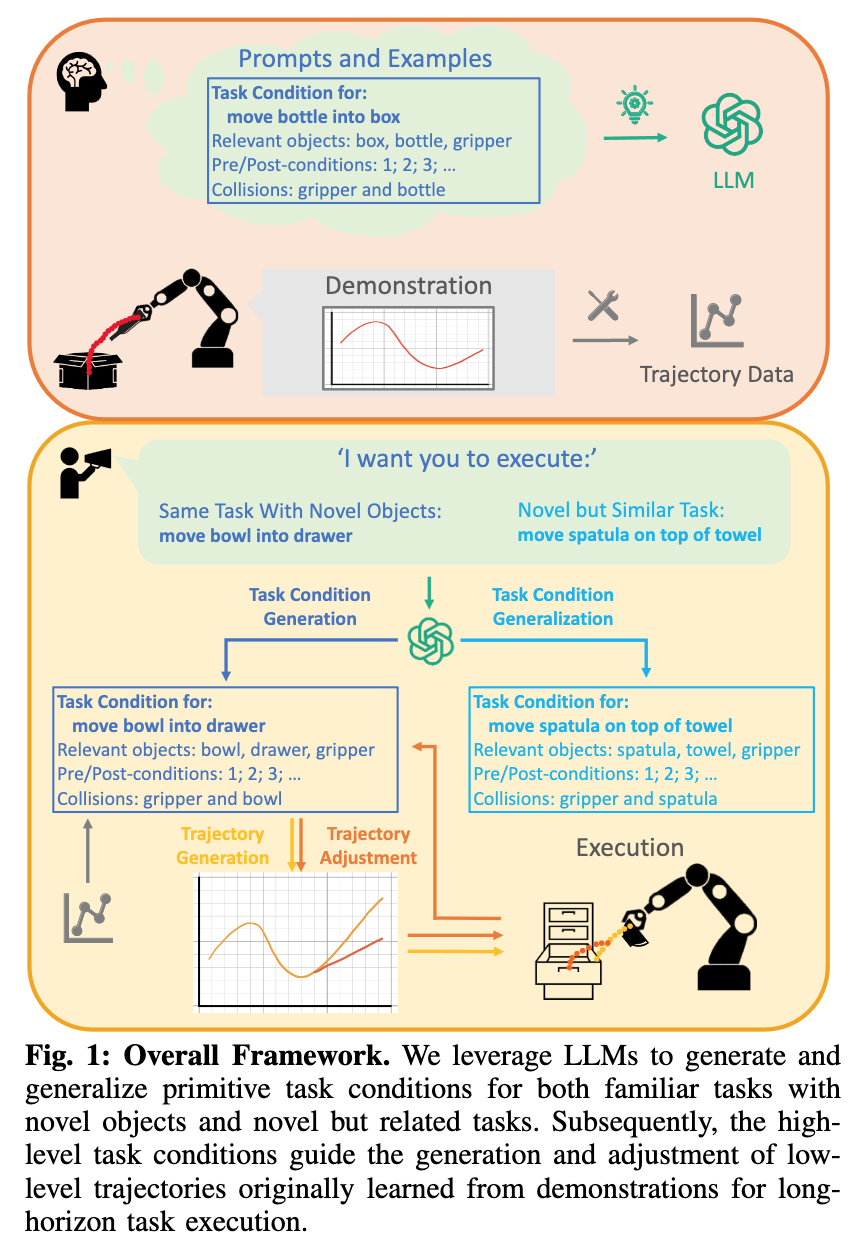
【AI视野·今日Robot 机器人论文速览 第四十七期】Wed, 4 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Wed, 4 Oct 2023 Totally 40 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚基于神经网络的多模态触觉感知, classification, position, posture, and force of the grasped object多模态形象的解耦(f…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
