2023CCPC网络赛(A E)
2023CCPC网络赛(A E)
The 2nd Universal Cup. Stage 3: Binjiang - Dashboard - Contest - Universal Cup Judging System
A. Almost Prefix Concatenation
思路:首先考虑如何求出每个位置允许失配一次的LCP长度 , 可以二分哈希求LCP , 即先二分一次求未失配的位置 , 向右扩展一位再次二分。
求出每个位置允许失配一次的LCP长度后考虑如何维护贡献 , 考虑最暴力的维护方式:
设计状态 dp[i][j] 为 i 位置及其后缀字符串分成 j 份 的方案数 , 这样显然很好转移。 但是时空双复杂度都是O(n^2) ,考虑优化 , 对于时间复杂度 , 我们不难发现 , 我们每次转移的位置都是一个区间 , 考虑后缀和优化 , O(1) 的进行转移。 对于空间复杂度 ,显然很难优化。转换思路 , 考虑直接维护平方贡献。
n o w 1 [ i ] 表示 i 所在后缀字符串划分的方案数 now1[i] ~表示 i所在后缀字符串划分的方案数 now1[i] 表示i所在后缀字符串划分的方案数
n o w 2 [ i ] 表示 i 所在后缀字符串划分的方案长度和 now2[i] ~表示i所在后缀字符串划分的方案长度和 now2[i] 表示i所在后缀字符串划分的方案长度和
n o w 3 [ i ] 表示 i 所在后缀字符串划分的方案长度平方和 now3[i] ~表示i所在后缀字符串划分的方案长度平方和 now3[i] 表示i所在后缀字符串划分的方案长度平方和
对于位置 i , 其转移区间显然是[i + 1 , i + lcp[i]] , 所以我们要对上面三个数组维护后缀和
s u f 1 [ i ] 为 n o w 1 [ i ] 的后缀和 suf1[i]~为now1[i]的后缀和 suf1[i] 为now1[i]的后缀和
s u f 2 [ i ] 为 n o w 2 [ i ] 的后缀和 suf2[i]~为now2[i]的后缀和 suf2[i] 为now2[i]的后缀和
s u f 3 [ i ] 为 n o w 3 [ i ] 的后缀和 suf3[i]~为now3[i]的后缀和 suf3[i] 为now3[i]的后缀和
对于转移:
不妨设 l = i + 1 , r = i + l c p [ i ] 不妨设 ~l=i+1,~r=i+lcp[i] 不妨设 l=i+1, r=i+lcp[i]
n o w 1 [ i ] = s u f 1 [ l ] − s u f 1 [ r + 1 ] (方案数直接转移) now1[i] = suf1[l] - suf1[r+1](方案数直接转移) now1[i]=suf1[l]−suf1[r+1](方案数直接转移)
n o w 2 [ i ] = s u f 2 [ l ] − s u f 2 [ r + 1 ] + n o w 1 [ i ] (每种方案长度都加 1 ) now2[i] = suf2[l] - suf2[r+1]+now1[i](每种方案长度都加1) now2[i]=suf2[l]−suf2[r+1]+now1[i](每种方案长度都加1)
n o w 3 [ i ] = ( s u f 3 [ l ] − s u f 3 [ r + 1 ] ) + 2 ∗ ( s u f 2 [ l ] − s u f 2 [ r + 1 ] ) + ( s u f 1 [ l ] − s u f 1 [ r + 1 ] ) [ 考虑 ( n + 1 ) 2 = n 2 + 2 ∗ n + 1 ] now3[i] = (suf3[l] - suf3[r+1])+2*(suf2[l]-suf2[r+1])+(suf1[l]-suf1[r+1])~~[考虑(n+1)^2=n^2+2*n+1] now3[i]=(suf3[l]−suf3[r+1])+2∗(suf2[l]−suf2[r+1])+(suf1[l]−suf1[r+1]) [考虑(n+1)2=n2+2∗n+1]
注意点:注意求LCP的时候双哈希即可 , 单哈希过不去。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int INF = 9e18;
const int N = 1e6 + 10;
const int mod = 998244353;
typedef pair<int,int>PII;
int n , m , lcp[N];
string s , t;const int mod1 = 1e9 + 7;
const int mod2 = 1e9 + 9;
const int Base = 131;int base1[N] , ht1[N] , base2[N] , ht2[N] , hs1[N] , hs2[N];
int suf1[N] , suf2[N] , suf3[N];
int now1[N] , now2[N] , now3[N];inline void init_hash(int n){base1[0] = base2[0] = 1;for(int i = 1 ; i <= n ; i ++) base1[i] = base1[i - 1] * Base % mod1;for(int i = 1 ; i <= n ; i ++) base2[i] = base2[i - 1] * Base % mod2;
}int add(int x , int y) {x %= mod;y %= mod;return (x + y) % mod;
}
int reduce(int x , int y) {x %= mod;y %= mod;return ((x - y) % mod + mod) % mod;
}inline PII get_s(int l,int r){int x = ((hs1[r] - hs1[l] * base1[r - l]) % mod1 + mod1) % mod1;int y = ((hs2[r] - hs2[l] * base2[r - l]) % mod2 + mod2) % mod2;return {x , y};
}inline PII get_t(int l,int r){int x = ((ht1[r] - ht1[l] * base1[r - l]) % mod1 + mod1) % mod1;int y = ((ht2[r] - ht2[l] * base2[r - l]) % mod2 + mod2) % mod2;return {x , y};
}signed main(){cin >> s >> t;n = s.size();m = t.size();init_hash(max(n , m));hs1[0] = hs2[0] = 0;for(int i = 1 ; i <= n ; i ++) hs1[i] = (hs1[i - 1] * Base % mod1 + s[i - 1]) % mod1;for(int i = 1 ; i <= n ; i ++) hs2[i] = (hs2[i - 1] * Base % mod2 + s[i - 1]) % mod2;ht1[0] = ht2[0] = 0;for(int i = 1 ; i <= m ; i ++) ht1[i] = (ht1[i - 1] * Base % mod1 + t[i - 1]) % mod1;for(int i = 1 ; i <= m ; i ++) ht2[i] = (ht2[i - 1] * Base % mod2 + t[i - 1]) % mod2;for(int i = 0 ; i < n ; i ++) {int l = i , r = min(i + m - 1 , n - 1) , mid = 0;while(l <= r) {mid = (l + r) >> 1;if(get_s(l , mid + 1) != get_t(l - i , mid + 1 - i)) r = mid - 1;else l = mid + 1;}int ll = l , rr = min(i + m - 1 , n - 1) , midd = 0;if(ll > rr) { lcp[i] = ll - i; continue; }ll += 1;if(ll > rr) { lcp[i] = ll - i; continue; }while(ll <= rr) {midd = (ll + rr) >> 1;if(get_s(ll , midd + 1) != get_t(ll - i , midd + 1 - i)) rr = midd - 1;else ll = midd + 1;}lcp[i] = ll - i;}suf1[n] = 1;for(int i = n - 1 ; i >= 0 ; i -- ){int l = i + 1 , r = i + lcp[i];now1[i] = reduce(suf1[l] , suf1[r + 1]);now2[i] = add(reduce(suf2[l] , suf2[r + 1]) , now1[i]);now3[i] = add(add(reduce(suf3[l] , suf3[r + 1]) , 2 * reduce(suf2[l] , suf2[r + 1])) , reduce(suf1[l] , suf1[r + 1]));suf1[i] = add(suf1[i + 1] , now1[i]);suf2[i] = add(suf2[i + 1] , now2[i]);suf3[i] = add(suf3[i + 1] , now3[i]); }cout << now3[0] << "\n";return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);/*
g1[i] i 点所在后缀切割方案数
g2[i] i 点所在后缀切割方案长度和
g3[i] i 点所在后缀切割方案长度平方和suf1[i] :now1[i] 的后缀和
suf2[i] :now2[i] 的后缀和
suf3[i] :now3[i] 的后缀和
*/
E. Robot Experiment
对于每个位置显然会有三个状态:
状态 1 :未走过 状态1:未走过 状态1:未走过
状态 2 :不能走 状态2:不能走 状态2:不能走
状态 3 :必须走 状态3:必须走 状态3:必须走
枚举所有可能 , 状态一进行讨论 , 状态二三直接搜索即可。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int INF = 9e18;
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int vis[110][110];
/*
0 可讨论
1 不能走
-1 必须走
*/int n ;
string s;
set<pair<int , int>>st;
void dfs(int x , int y , int pos) {if(pos == n) {st.insert({x , y});return ;}int xx = x , yy = y;if(s[pos] == 'L') xx -= 1;if(s[pos] == 'R') xx += 1;if(s[pos] == 'U') yy += 1;if(s[pos] == 'D') yy -= 1;if(vis[xx + 50][yy + 50] == 0) {vis[xx + 50][yy + 50] = 1;dfs(x , y , pos + 1);vis[xx + 50][yy + 50] = 0;vis[xx + 50][yy + 50] = -1;dfs(xx , yy , pos + 1);vis[xx + 50][yy + 50] = 0;}if(vis[xx + 50][yy + 50] == 1) {dfs(x , y , pos + 1);}if(vis[xx + 50][yy + 50] == -1) {dfs(xx , yy , pos + 1);}}signed main(){IOScin >> n >> s;vis[50][50] = -1;dfs(0 , 0 , 0);cout << st.size() << "\n";for(auto [x , y] : st) {cout << x << " " << y << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
)
2023CCPC网络赛(A E)
2023CCPC网络赛(A E) The 2nd Universal Cup. Stage 3: Binjiang - Dashboard - Contest - Universal Cup Judging System A. Almost Prefix Concatenation 思路:首先考虑如何求出每个位置允许失配一次的LCP长度 , 可以二分哈希求LCP , 即…...

使用 python 检测泛洪攻击的案例
使用 python 检测泛洪攻击的案例 本案例只使用python标准库通过执行命令来监控异常请求, 并封锁IP, 不涉及其他第三方库工具. import os import time from collections import Counter# 1、update 命令, 采集CPU的平均负载 def get_cpu_load():"""uptime 命令…...

SCROLLINFO scrollInfo; 2023/10/5 下午3:38:53
2023/10/5 下午3:38:53 SCROLLINFO scrollInfo;scrollInfo.cbSize = sizeof(SCROLLINFO);scrollInfo.fMask = SIF_ALL;//scrollInfo.nMin = 0; // 最小位置//scrollInfo.nMax = nRowCountToShow; // 最大位置//scrollInfo.nPage = nRowCountToShow; // 页面大小//scrollInf…...

Python--控制台获取输入与正则表达式
前言一、控制台获取输入1.1 字符串输入1.2 整数输入1.3 浮点数输入1.4 布尔值输入1.5 列表输入1.6 汇总 二、正则表达式2.1 匹配数字2.2 模式检查2.3 替换字符2.4 切分字符串2.5 搜索并提取匹配的部分2.6 使用捕获组提取匹配的部分2.7 非贪婪匹配2.8 忽略大小写匹配2.9 使用预定…...
网络基础知识面试题1
VC++常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C++软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...)...

JavaScript系列从入门到精通系列第十五篇:JavaScript中函数的实参介绍返回值介绍以及函数的立即执行
文章目录 一:函数的参数 1:形参如何定义 2:形参的使用规则 二:函数的返回值 1:函数返回值如何定义 2:函数返回值种类 三:实参的任意性 1:方法可以作为实参 2:将匿…...
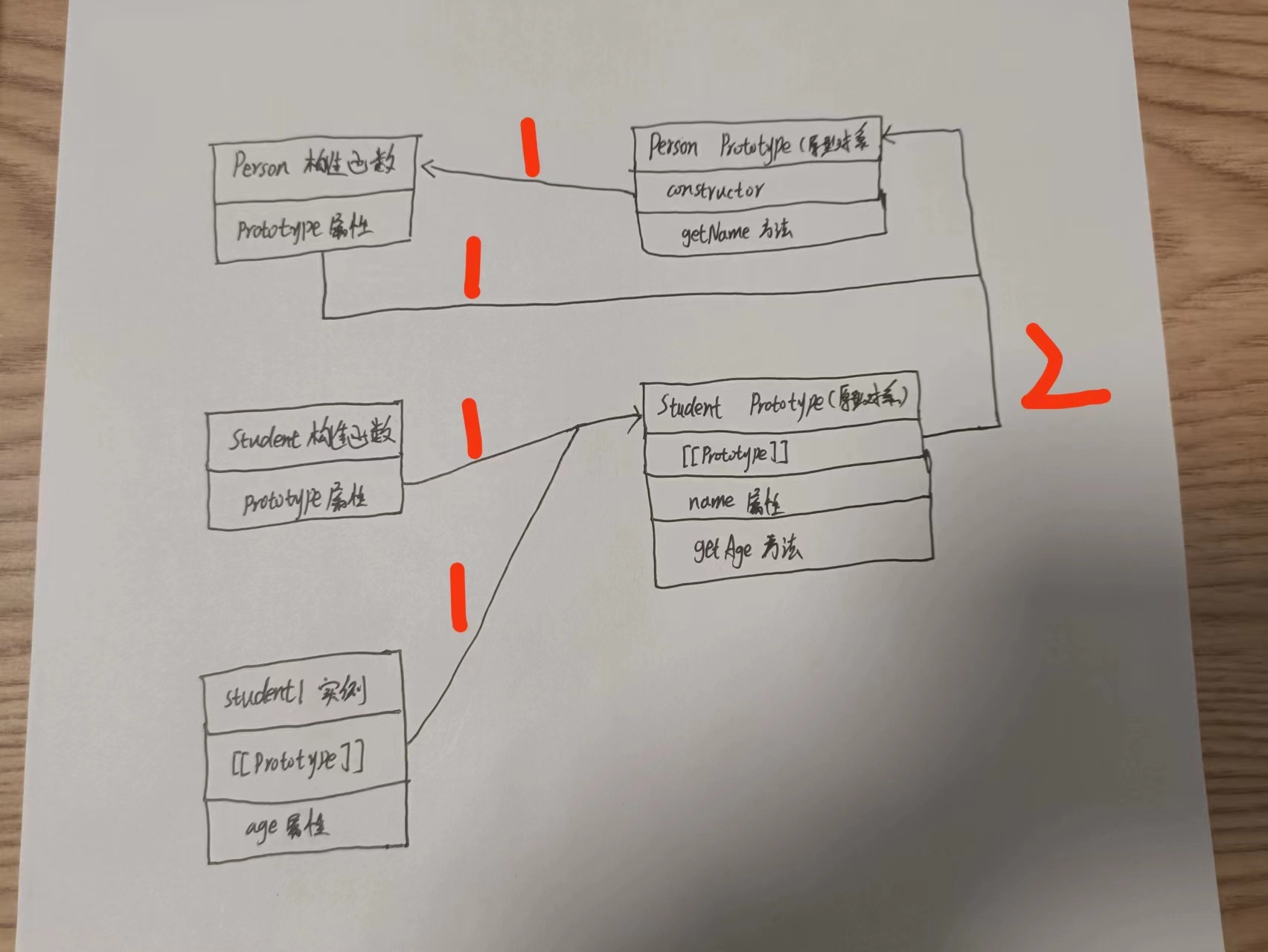
js中的原型链
编写思路: 简单介绍构造函数介绍原型对象原型对象、实例的关系,从而引出原型链的基本概念 原型链基本思想是利用原型让一个引用类型继承另一个引用类型的属性和方法。 1. 什么是构造函数 构造函数本身跟普通函数一样,也不存在定义构造函数…...
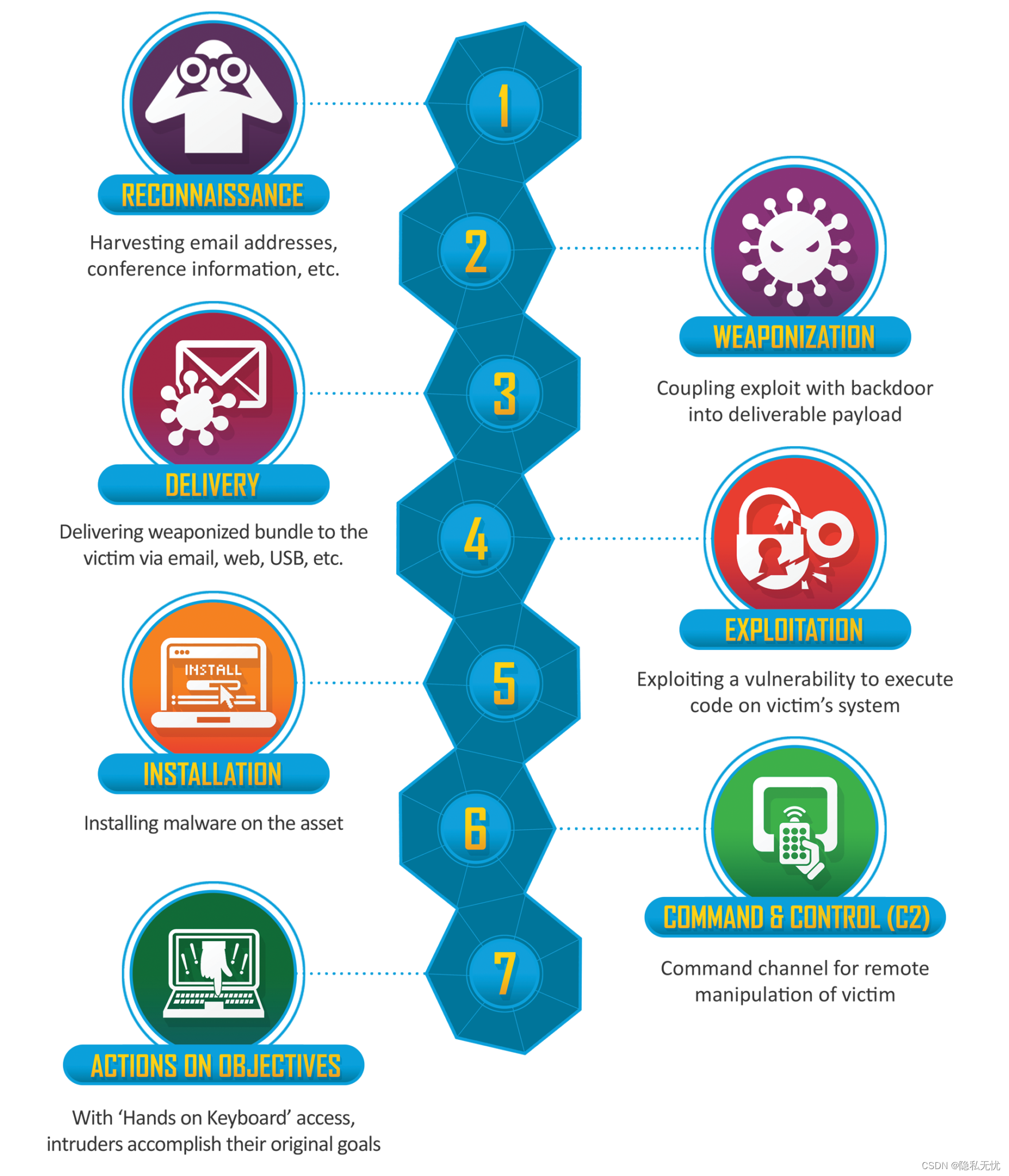
一文搞懂APT攻击
APT攻击 1. 基本概念2. APT的攻击阶段3. APT的典型案例参考 1. 基本概念 高级持续性威胁(APT,Advanced Persistent Threat),又叫高级长期威胁,是一种复杂的、持续的网络攻击,包含高级、长期、威胁三个要素…...

在pandas中通过一列数据映射出另一列的几种思路和方法
如果一句话中出现某个品牌的关键词,那么就将该品牌进行提取,开始我的做法是写了很多elif,如下: def brand_describe(x):if TRUM in x.upper():return "通快"elif BYSTRONIC in x.upper():return "百超"elif …...
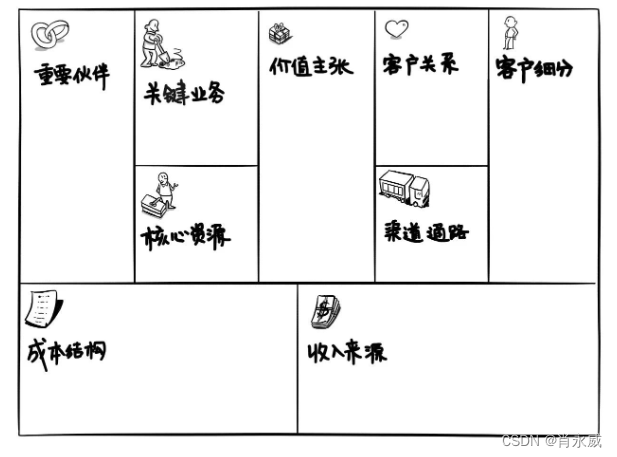
数据分析视角中的商业分析学习笔记
数据分析一大堆,结果却是大家早就知道的结论?是工具和方法出问题了吗?真正原因可能是你的思维有误区。 为什么分析的这么辛苦,得出的结论大家早知道,谁谁都不满意?核心原因有3个: 分析之前&am…...
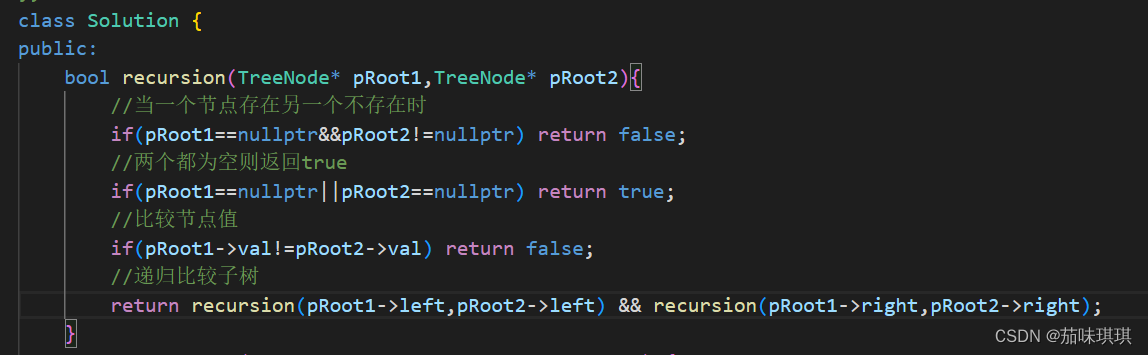
剑指offer——JZ26 树的子结构 解题思路与具体代码【C++】
一、题目描述与要求 树的子结构_牛客题霸_牛客网 (nowcoder.com) 题目描述 输入两棵二叉树A,B,判断B是不是A的子结构。(我们约定空树不是任意一个树的子结构) 假如给定A为{8,8,7,9,2,#,#,#,#,4,7},B为{8,9,2}&…...

NEFU数字图像处理(1)绪论
一、简介 1.1什么是数字图像 图像是三维场景在二维平面上的影像。根据其存储方式和表现形式,可以将图像分为模拟图像和数字图像两大类 图像处理方法:光学方法、电子学方法 模拟图像:连续的图像数字图像:通过对时间上和数值上连续…...
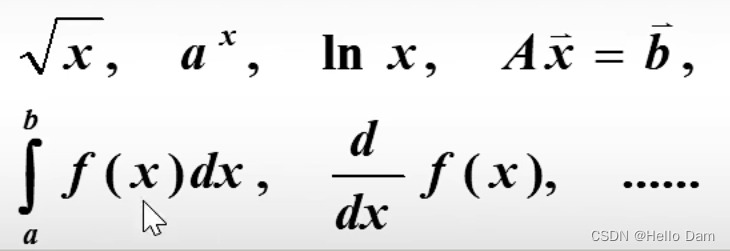
数值分析学习笔记——绪论【华科B站教程版本】
绪论 数值分析概念 用计算机求解数学问题的数值方法和理论 三大科学研究方法 实验理论分析科学计算(用计算机去辅助研究):数值方法计算机 解析解和近似解 解析解:使用数学方法求出或推导出的结果,往往可以求解出…...

节日灯饰灯串灯出口欧洲CE认证办理
灯串(灯带),这个产品的形状就象一根带子一样,再加上产品的主要原件就是LED,因此叫做灯串或者灯带。2022年,我国灯具及相关配件产品出口总额超过460亿美元。其中北美是最大的出口市场。其次是欧洲市场&#…...
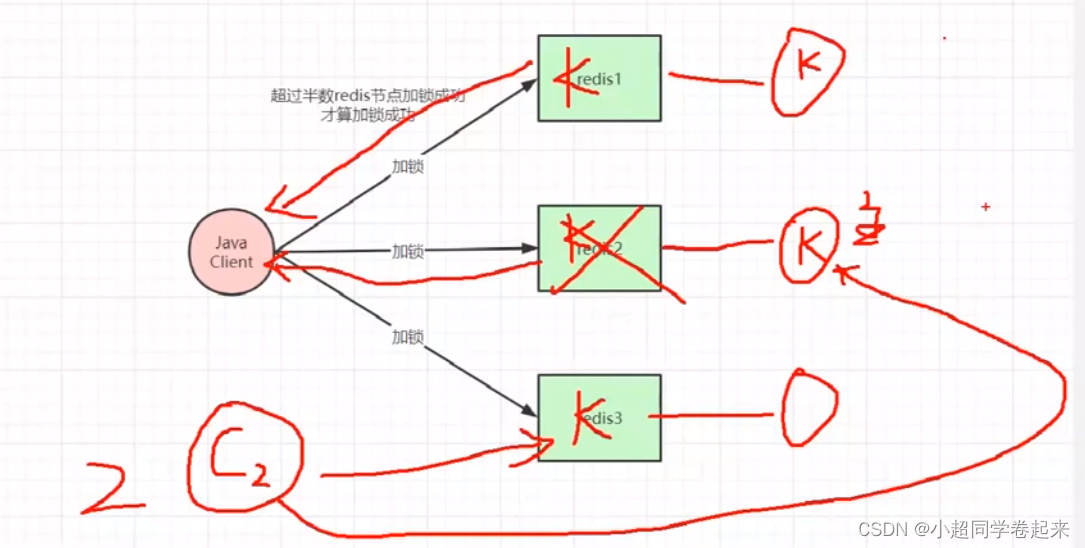
一线大厂Redis高并发缓存架构实战与性能优化
文章目录 一、redis主从架构锁失效问题分析二、从CAP角度剖析redis与zookeeper分布式锁区别三、redlock分布式锁原理与存在的问题分析四、大促场景如何将分布式锁性能提升100倍五、高并发redis架构代码实战 一、redis主从架构锁失效问题分析 我们都知道,一般的互联…...

PHP 行事准则:allow_url_fopen 与 allow_url_include
文章目录 参考环境allow_url_fopenallow_url_fopen 配置项操作远程文件file 协议 allow_url_includeallow_url_include 配置项 allow_url_include 与 allow_url_fopen区别联系默认配置配置项关闭所导致异常运行时配置ini_set()限制 参考 项目描述搜索引擎Bing、GoogleAI 大模型…...
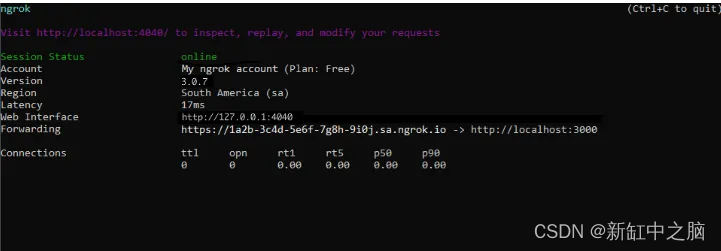
Replicate + ngrok云端大模型API实现教程
ChatGPT 的诞生预示着人工智能和机器学习领域的新时代。 日新月异,Hugging Face 不断推出突破性的语言模型,重新定义人机交互的界限。欢迎来到未来! 当然,有很多选项可以对它们进行推断。在本文中,我将告诉大家如何使…...

蓝桥等考Python组别十四级005
蓝桥等考Python组别十四级 第一部分:选择题 1、Python L14 (15分) 运行下面程序,输出的结果是( )。 d = {1 : one, 2 : two, 3 : three, 4 : four} print(d[2]) onetwothreefour正确答案:B...
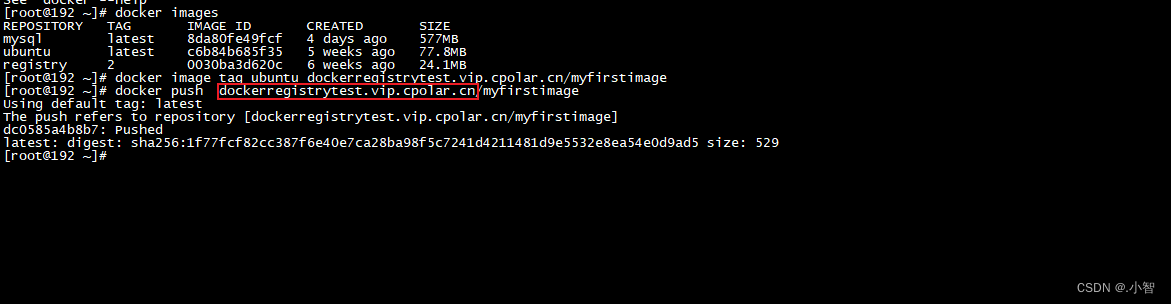
Linux 本地 Docker Registry本地镜像仓库远程连接
Linux 本地 Docker Registry本地镜像仓库远程连接 Docker Registry 本地镜像仓库,简单几步结合cpolar内网穿透工具实现远程pull or push (拉取和推送)镜像,不受本地局域网限制! 1. 部署Docker Registry 使用官网安装方式,docker命令一键启动,该命令启动一个regis…...
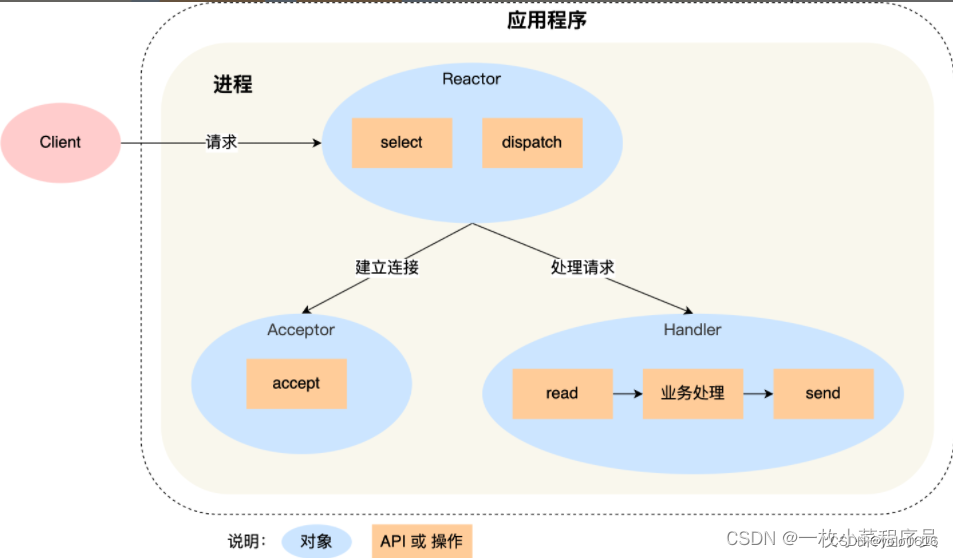
二十九、高级IO与多路转接之epollreactor(收官!)
文章目录 一、Poll(一)定义(二)实现原理(三)优点(四)缺点 二、I/O多路转接之epoll(一)从网卡接收数据说起(二)如何知道接收了数据&…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
