【数据结构与算法】之“堆”介绍
目录
堆的基本存储
一、概念及其介绍
二、适用说明
三、结构图示
堆的 shift up
堆的 shift down
基础堆排序
一、概念及其介绍
二、适用说明
三、过程图示
优化堆排序
索引堆及其优化
一、概念及其介绍
二、适用说明
三、结构图示
堆的基本存储
一、概念及其介绍
堆(Heap)是计算机科学中一类特殊的数据结构的统称。
堆通常是一个可以被看做一棵完全二叉树的数组对象。
堆满足下列性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值。
- 堆总是一棵完全二叉树。
二、适用说明
堆是利用完全二叉树的结构来维护一组数据,然后进行相关操作,一般的操作进行一次的时间复杂度在 O(1)~O(logn) 之间,堆通常用于动态分配和释放程序所使用的对象。
若为优先队列的使用场景,普通数组或者顺序数组,最差情况为 O(n^2),堆这种数据结构也可以提高入队和出队的效率。
| 入队 | 出队 | |
|---|---|---|
| 普通数组 | O(1) | O(n) |
| 顺序数组 | O(n) | O(1) |
| 堆 | O(logn) | O(log) |
三、结构图示
二叉堆是一颗完全二叉树,且堆中某个节点的值总是不大于其父节点的值,该完全二叉树的深度为 k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边。
其中堆的根节点最大称为最大堆,如下图所示:

我们可以使用数组存储二叉堆,右边的标号是数组的索引。
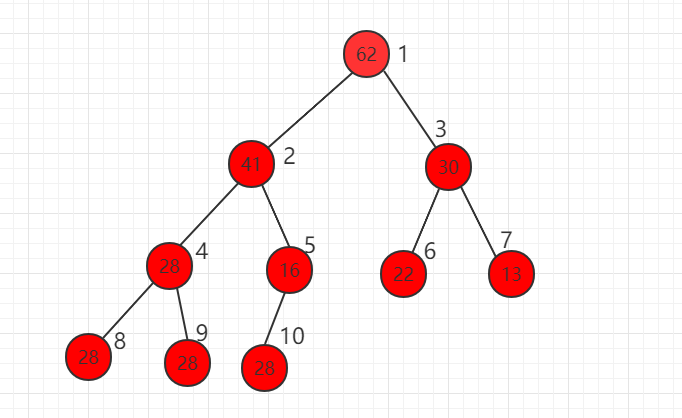
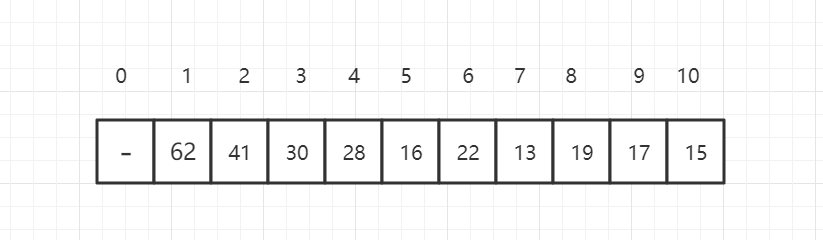
假设当前元素的索引位置为 i,可以得到规律:
parent(i) = i/2(取整)
left child(i) = 2*i
right child(i) = 2*i +1堆的 shift up
本小节介绍如何向一个最大堆中添加元素,称为 shift up。
假设我们对下面的最大堆新加入一个元素52,放在数组的最后一位,52大于父节点16,此时不满足堆的定义,需要进行调整。
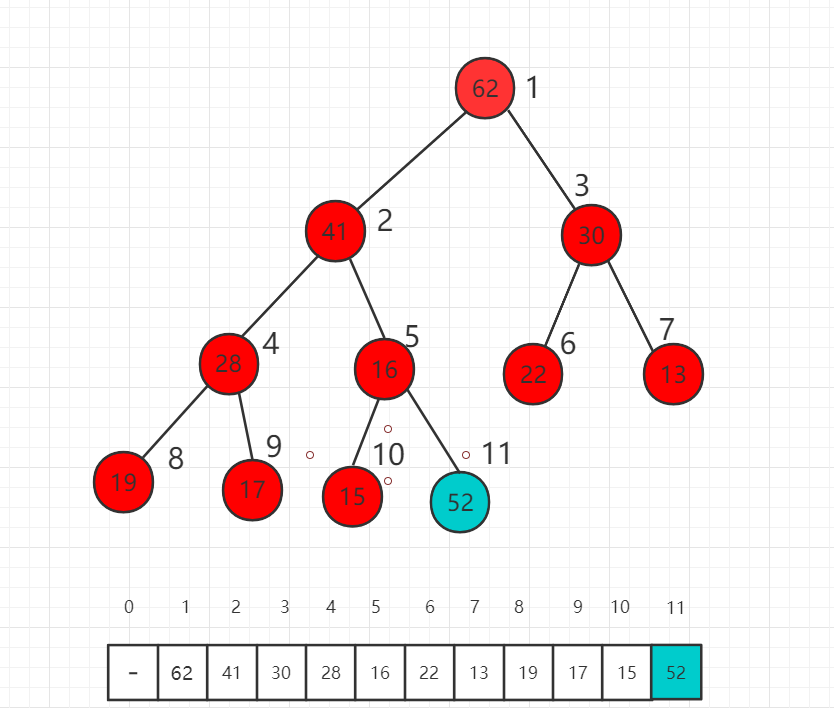
首先交换索引为 5 和 11 数组中数值的位置,也就是 52 和 16 交换位置。
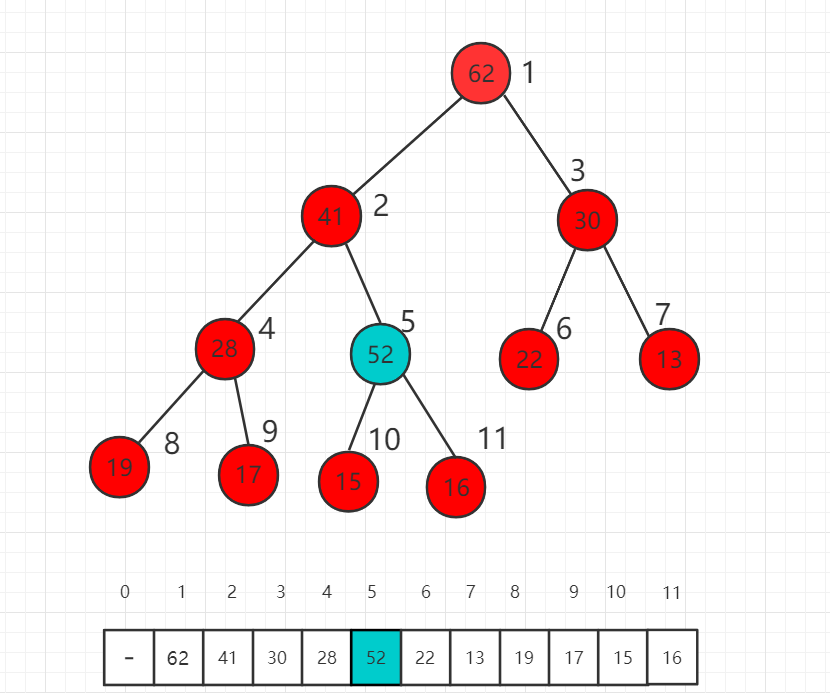
此时 52 依然比父节点索引为 2 的数值 41 大,我们还需要进一步挪位置。
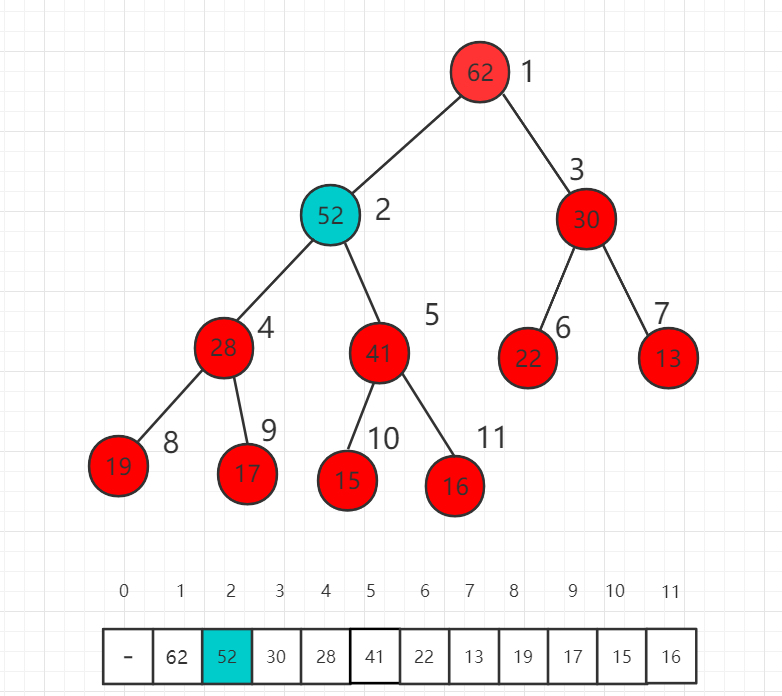
这时比较 52 和 62 的大小,52 已经比父节点小了,不需要再上升了,满足最大堆的定义。我们称这个过程为最大堆的 shift up。
堆的 shift down
本小节将介绍如何从一个最大堆中取出一个元素,称为 shift down,只能取出最大优先级的元素,也就是根节点,把原来的 62 取出后,下面介绍如何填补这个最大堆。
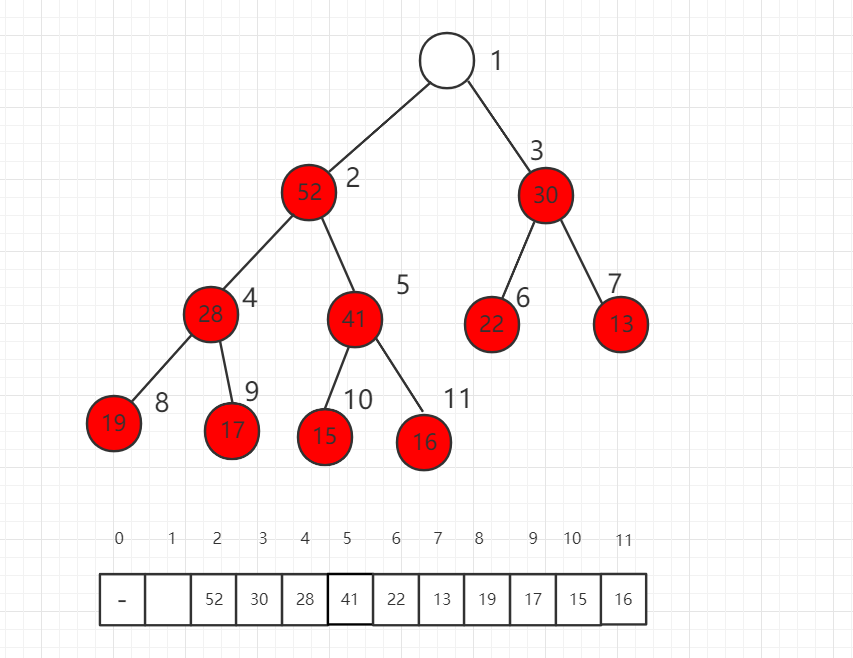
第一步,我们将数组最后一位数组放到根节点,此时不满足最大堆的定义。
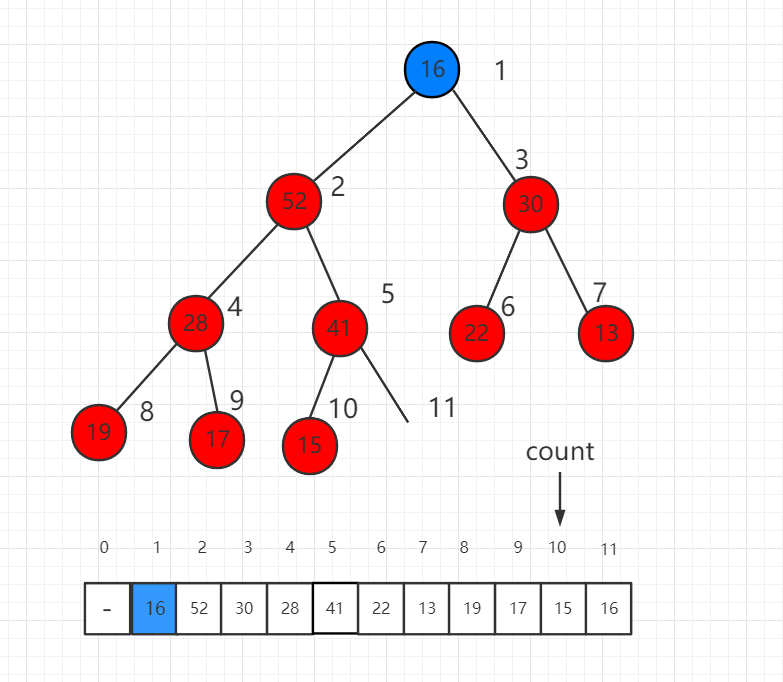
调整的过程是将这个根节点 16 一步一步向下挪,16 比子节点都小,先比较子节点 52 和 30 哪个大,和大的交换位置。
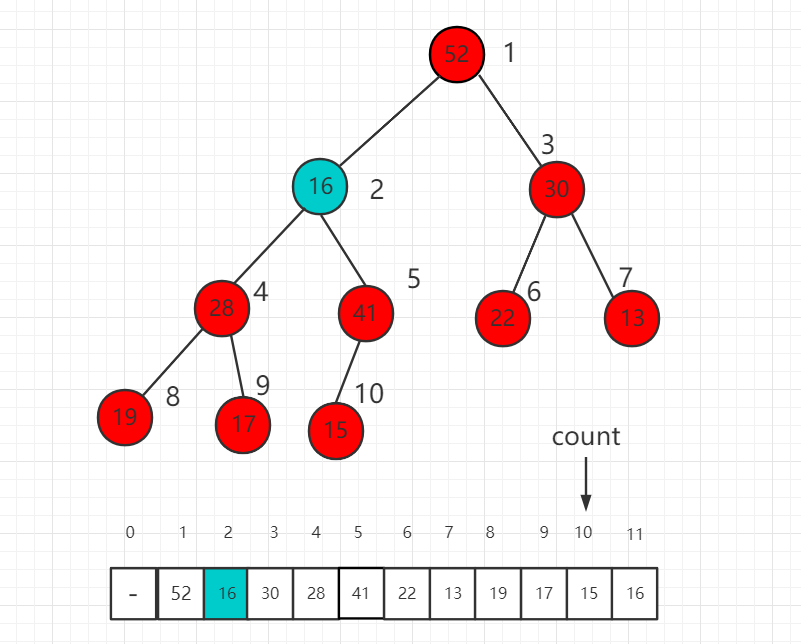
继续比较 16 的子节点 28 和 41,41 大,所以 16 和 41 交换位置。

继续 16 和孩子节点 15 进行比较,16 大,所以现在不需要进行交换,最后我们的 shift down 操作完成,维持了一个最大堆的性质。
基础堆排序
一、概念及其介绍
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。
堆是一个近似 完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
二、适用说明
我们之前构造堆的过程是一个个数据调用 insert 方法使用 shift up 逐个插入到堆中,这个算法的时候时间复杂度是 O(nlogn),本小节介绍的一种构造堆排序的过程,称为 Heapify,算法时间复杂度为 O(n)。
三、过程图示
完全二叉树有个重要性质,对于第一个非叶子节点的索引是 n/2 取整数得到的索引值,其中 n 是元素个数(前提是数组索引从 1 开始计算)。
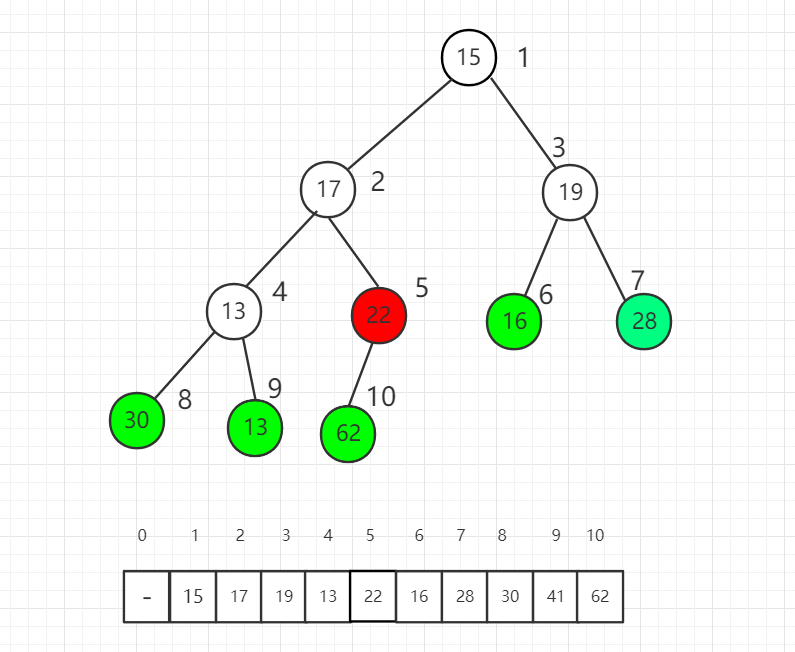
索引 5 位置是第一个非叶子节点,我们从它开始逐一向前分别把每个元素作为根节点进行 shift down 操作满足最大堆的性质。
索引 5 位置进行 shift down 操作后,22 和 62 交换位置。

对索引 4 元素进行 shift down 操作

对索引 3 元素进行 shift down 操作
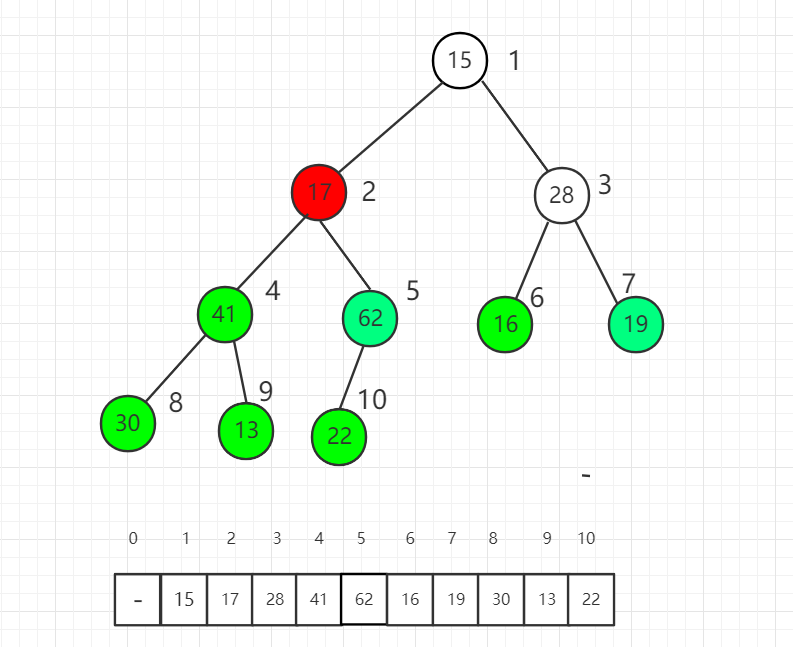
对索引 2 元素进行 shift down 操作
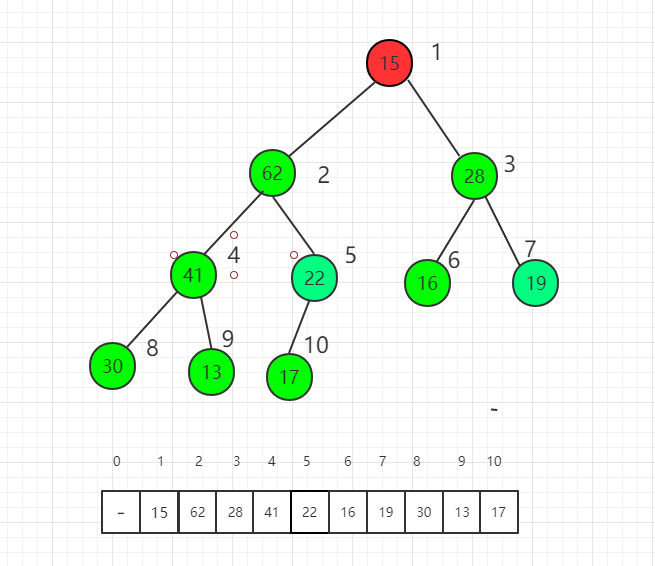
最后对根节点进行 shift down 操作,整个堆排序过程就完成了。

优化堆排序
上一节的堆排序,我们开辟了额外的空间进行构造堆和对堆进行排序。这一小节,我们进行优化,使用原地堆排序。
对于一个最大堆,首先将开始位置数据和数组末尾数值进行交换,那么数组末尾就是最大元素,然后再对W元素进行 shift down 操作,重新生成最大堆,然后将新生成的最大数和整个数组倒数第二位置进行交换,此时倒数第二位置就是倒数第二大数据,这个过程以此类推。
整个过程可以用如下图表示:

索引堆及其优化
一、概念及其介绍
索引堆是对堆这个数据结构的优化。
索引堆使用了一个新的 int 类型的数组,用于存放索引信息。
相较于堆,优点如下:
- 优化了交换元素的消耗。
- 加入的数据位置固定,方便寻找。
二、适用说明
如果堆中存储的元素较大,那么进行交换就要消耗大量的时间,这个时候可以用索引堆的数据结构进行替代,堆中存储的是数组的索引,我们相应操作的是索引。
三、结构图示
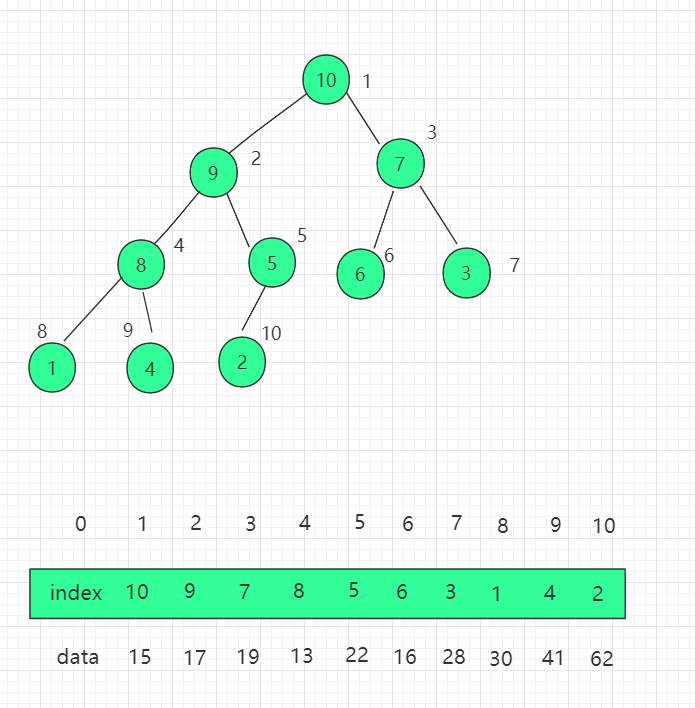
我们需要对之前堆的代码实现进行改造,换成直接操作索引的思维。首先构造函数添加索引数组属性 indexes。
protected T[] data; // 最大索引堆中的数据
protected int[] indexes; // 最大索引堆中的索引
protected int count;
protected int capacity;相应构造函数调整为,添加初始化索引数组。
...
public IndexMaxHeap(int capacity){data = (T[])new Comparable[capacity+1];indexes = new int[capacity+1];count = 0;this.capacity = capacity;
}
...调整插入操作,indexes 数组中添加的元素是真实 data 数组的索引 indexes[count+1] = i。
...
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
public void insert(int i, Item item){assert count + 1 <= capacity;assert i + 1 >= 1 && i + 1 <= capacity;i += 1;data[i] = item;indexes[count+1] = i;count ++;shiftUp(count);
}
...调整 shift up 操作:比较的是 data 数组中父节点数据的大小,所以需要表示为 data[index[k/2]] < data[indexs[k]],交换 index 数组的索引,对 data 数组不产生任何变动,shift down 同理。
...
//k是堆的索引
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftUp(int k){while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) < 0 ){swapIndexes(k, k/2);k /= 2;}
}
...从索引堆中取出元素,对大元素为根元素 data[index[1]] 中的数据,然后再交换索引位置进行 shift down 操作。
...
public T extractMax(){assert count > 0;T ret = data[indexes[1]];swapIndexes( 1 , count );count --;shiftDown(1);return ret;
}
...也可以直接取出最大值的 data 数组索引值
...
// 从最大索引堆中取出堆顶元素的索引
public int extractMaxIndex(){assert count > 0;int ret = indexes[1] - 1;swapIndexes( 1 , count );count --;shiftDown(1);return ret;
}
...修改索引位置数据
...
// 将最大索引堆中索引为i的元素修改为newItem
public void change( int i , Item newItem ){i += 1;data[i] = newItem;// 找到indexes[j] = i, j表示data[i]在堆中的位置// 之后shiftUp(j), 再shiftDown(j)for( int j = 1 ; j <= count ; j ++ )if( indexes[j] == i ){shiftUp(j);shiftDown(j);return;}
}
...相关文章:

【数据结构与算法】之“堆”介绍
目录 堆的基本存储 一、概念及其介绍 二、适用说明 三、结构图示 堆的 shift up 堆的 shift down 基础堆排序 一、概念及其介绍 二、适用说明 三、过程图示 优化堆排序 索引堆及其优化 一、概念及其介绍 二、适用说明 三、结构图示 堆的基本存储 一、概念及其介…...
 使用GPU加速崩溃)
ncnn Fatal signal 11 (SIGSEGV) 使用GPU加速崩溃
如果你的报错堆栈中包含以下信息,其中的关键信息是 anon:dalvik-classes2.dex extracted in memory Fatal signal 11 (SIGSEGV), code 1 (SEGV_MAPERR), fault addr 0x3c in tid 8619 (eplabv3plusncnn), pid 8619 () 2023-10-07 15:48:31.395 9793-9793 DEBUG …...

计算机考研 | 2018年 | 计算机组成原理真题
文章目录 【计算机组成原理2018年真题44题-15分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2018年真题45题-8分】【第一步:信息提取】【第二步:具体解答】 【计算机组成原理2018年真题44题-15分】 某计算机采用页…...

用Configuration注解的方式写一个java过滤器的详细实例?
在Java中,可以使用Configuration注解和Spring框架来创建和配置过滤器。下面是一个详细的示例: 首先,创建一个实现javax.servlet.Filter接口的过滤器类,例如MyFilter: import javax.servlet.*; import java.io.IOExce…...
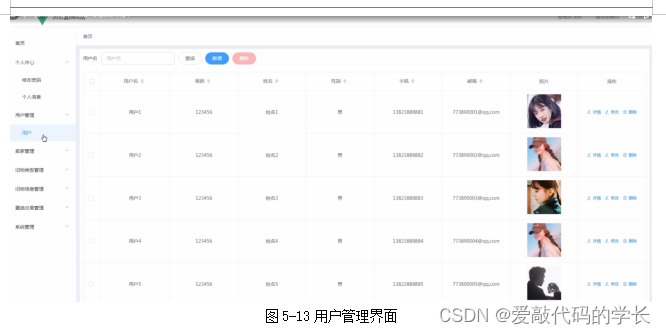
基于Springboot实现旧物置换网站平台演示【项目源码+论文说明】分享
基于Springboot实现旧物置换网站平台演示 摘要 随着时代在一步一步在进步,旧物也成人们的烦恼,许多平台网站都在推广自已的产品像天猫、咸鱼、京东。所以开发出一套关于旧物置换网站成为必需。旧物置换网站主要是借助计算机,通过对用户进行管…...

想要精通算法和SQL的成长之路 - 存在重复元素
想要精通算法和SQL的成长之路 - 存在重复元素 前言一. 存在重复元素II二. 存在重复元素III2.1 基于红黑树增删改查 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 存在重复元素II 原题链接 思路: 我们用HashSet存储元素,做到去重的效果。同时存储…...
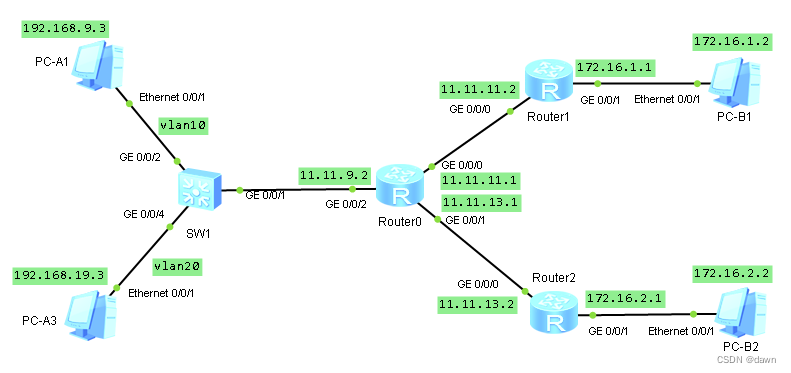
使用华为eNSP组网试验⑸-访问控制
今天练习使用华为sNSP模拟网络设备上的访问控制,这样的操作我经常在华为的S7706、S5720、S5735或者H3C的S5500、S5130、S7706上进行,在网络设备上根据情况应用访问控制的策略是一个网管必须熟练的操作,只是在真机上操作一般比较谨慎ÿ…...
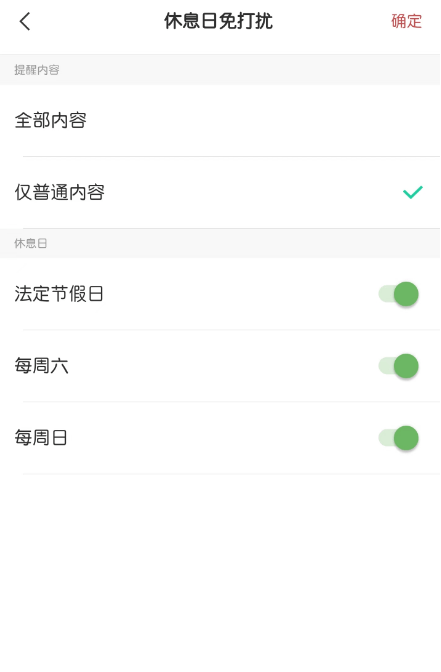
iPhone苹果手机闹钟智能跳过节假日怎么设置?
国内绝大多数的手机用户使用的操作系统只有三个,安卓、鸿蒙和苹果的ios。而iPhone苹果手机的忠实用户是非常多的,所以日积月累中用户数量也就非常庞大,并且相当一部分用户都是上班族。而工作忙碌的上班族因为事情比较多,为了避免自…...
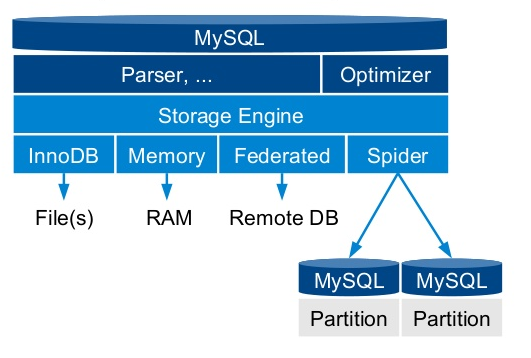
TenDB Cluster 简介
文章目录 1.简介2.TSpider3.TenDB4.Tdbctl5.TenDB Cluster Operator参考文献 1.简介 TenDB Cluster 是腾讯游戏 CROS DBA 团队提供的 MySQL 分布式关系型数据库解决方案。主要特点包括:透明分库分表、高可用的 MySQL 集群服务,透明及在线的扩容及缩容&a…...
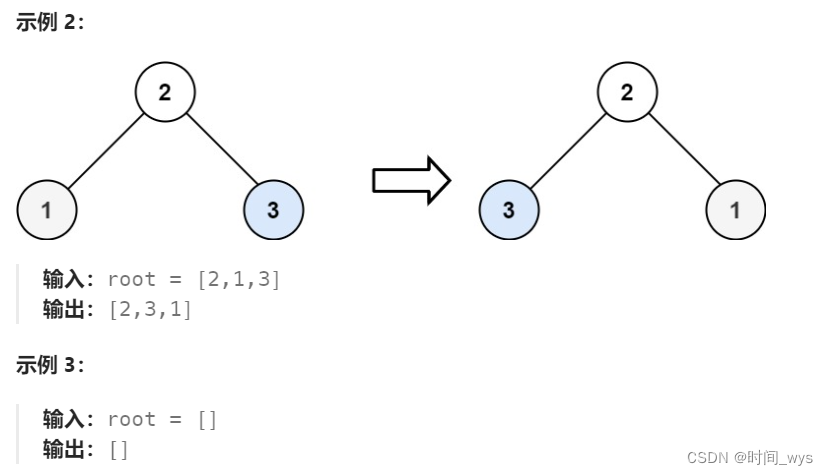
【刷题笔记10.6】LeetCode:翻转二叉树
LeetCode:翻转二叉树 一、题目描述 给你一颗二叉树的根节点root,翻转这颗二叉树,并返回其根节点。 二、分析 我们在做二叉树题目时候,第一想到的应该是用 递归 来解决。 仔细看下题目的 输入 和 输出,输出的左右…...
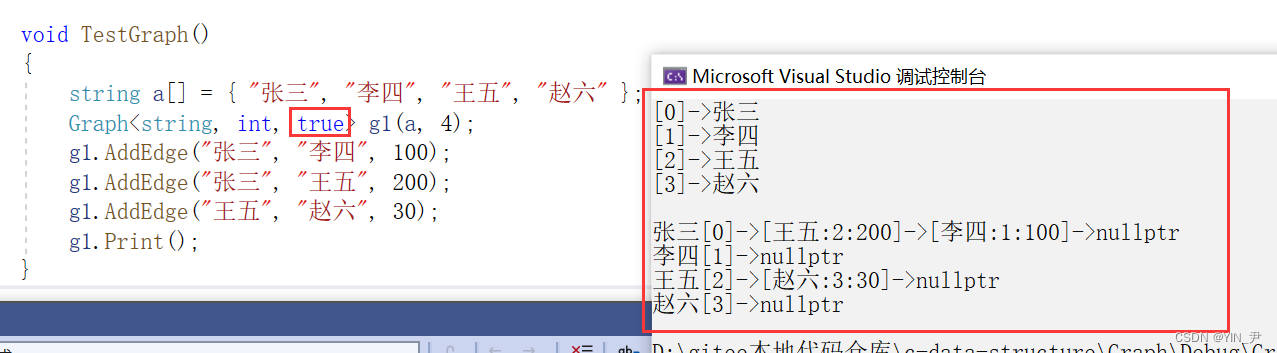
【高阶数据结构】图详解第一篇:图的基本概念及其存储结构(邻接矩阵和邻接表)
文章目录 1. 图的基本概念1.1 什么是图1.2 有向图和无向图1.3 完全图1.4 邻接顶点1.5 顶点的度1.6 路径1.7 路径长度1.8 简单路径与回路1.9 子图1.10 连通图1.11 强连通图1.12 生成树 2. 图的存储结构2.1 邻接矩阵2.2 邻接矩阵代码实现结构定义构造函数添加边打印图测试 2.3 邻…...

IPV4跟IPV6的区别
如今互联网快速发展ipv4已经满足不了现在的需求,那么这时候就需要用更大的地址空间来代替,这时候ipv6就可以满足这一需求,相比ipv4它有更大的地址空间可供使用。下面我将分享一下有何区别。 IPv4与IPv6之间的区别: 1、地址长度的区别:IPv4具…...
利用fitnesse实现api接口自动化测试
上午在园子里乱逛,看了不少小伙伴们分享的接口测试方面的知识,仔细想想,我做接口测试也有几个年头了,大家所叙述到的一些经验或多或少,我也曾遇到过,突然意识到知识的点滴积累是多么的重要,我记…...

【LeetCode】1154.一年中的第几天
题目描述: 给你一个字符串 date ,按 YYYY-MM-DD 格式表示一个 现行公元纪年法 日期。返回该日期是当年的第几天。 示例 1: 输入:date "2019-01-09" 输出:9 解释:给定日期是2019年的第九天。示…...
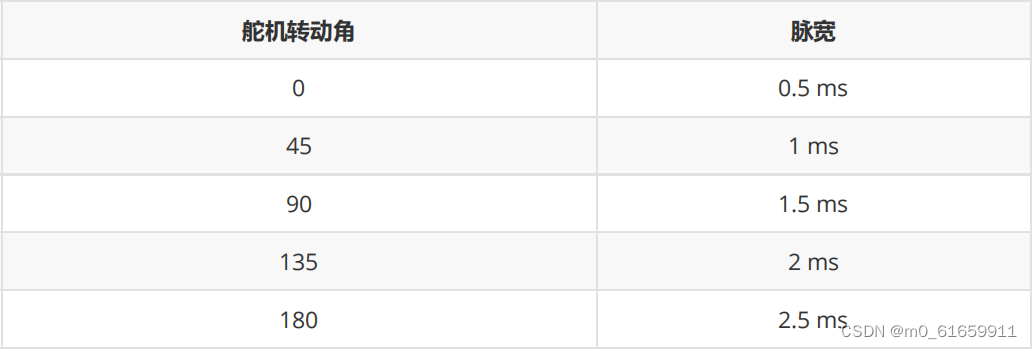
4.物联网射频识别,RFID开发【智能门禁项目】
补充:学习路径 一。项目介绍及需求分析 1.酒店智能门禁使用场景介绍 1.客人入住 客人在前台办理入住手续,前台管理员通过门禁管理系统为客户开一张门禁卡 客户持卡到相应客房,用IC 卡刷卡开门 客人过了入住时间后,卡自动失效&a…...

CompletableFuture 和 Future 的选择,以及CompletableFuture的用法
在 Java 编程中,异步编程是一种重要的技术,它允许你在执行长时间运行的任务时不会阻塞主线程。为了支持异步编程,Java 提供了 Future 和 CompletableFuture 这两个关键的类。在本文中,我们将比较它们的特点、优缺点以及使用场景。…...

美国第三大财产和意外险公司利宝保险集团利用 OpenText EnCase 取证收集技术控制法律风险和成本
美国第三大财产和意外险公司利宝保险集团利用 OpenText EnCase 取证收集技术控制法律风险和成本 利宝保险集团通过内部取证收集技术控制法律风险和成本。OpenText EnCase Information Assurance(以前称为 EnCase eDiscovery)使保险公司巨头能够自信高效地…...

打包报错JavaScript heap out of memory
npm run build 的时候出现了Reached heap limit Allocation failed - JavaScript heap out of memory,报错信息如下图所示。 奇怪的时候这个报错信息在本地不会出现,通过jekins在服务器打包部署的时候才会出现。于是进入服务器执行下面一句代码ÿ…...

Android Camera FW 里的requestId和frameId
安卓相机frameworks里面经常出现requestId和frameId,最近简单看了一下代码,发现相关流程还是很复杂的,总结来看requestId 就是上层(java)发送的repeating(capture)请求的id,是从0开始递增的。 这是CameraD…...

代理IP与Socks5代理在技术世界的多元应用
在数字化时代,网络工程师的任务不仅是维护网络的稳定性,还需要应对各种技术挑战。代理IP与Socks5代理作为技术工具箱中的两把利器,在跨界电商、爬虫、出海业务、网络安全和游戏领域中发挥了关键作用。本文将深入探讨这两项技术在不同领域的多…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
