矩阵的相似性度量的常用方法
矩阵的相似性度量的常用方法
1,欧氏距离
欧式距离是最易于理解的一种距离计算方法,源自欧式空间中两点间的距离公式。
(1)二维平面上的点 a ( x 1 , y 1 ) a(x_1,y_1) a(x1,y1)和点 b ( x 2 , y 2 ) b(x_2,y_2) b(x2,y2)的欧式距离为
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} d=(x1−x2)2+(y1−y2)2
(2)三维平面上的点 a ( x 1 , y 1 , z 1 ) a(x_1,y_1,z_1) a(x1,y1,z1)和点 b ( x 2 , y 2 , z − 2 ) b(x_2,y_2,z-2) b(x2,y2,z−2)的欧式距离为
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2} d=(x1−x2)2+(y1−y2)2+(z1−z2)2
不失一般性:
D ( X i , X j ) = ∑ l = 1 d ( x i l − x j l ) 2 D(X_i,X_j)=\sqrt{\sum_{l=1}^d(x_{il}-x_{jl})^2} D(Xi,Xj)=∑l=1d(xil−xjl)2
其中:D表示样本间的距离, X i , X j X_i,X_j Xi,Xj代表一个向量,或称为样本点或者样本;l是样本特征的维数, x i l , x j l x_{il},x_{jl} xil,xjl表示一个变量,或成为属性;d表示样本的总维数,即样本特征的总数量(下同)。
2,切比雪夫距离
在二维空间中,切比雪夫距离的典型应用是解决国际象棋中的国王从一个格子走到另一个格子最少需要几步的问题。这种距离在模糊C-Means方法中得到了有效应用。切比雪夫距离的公式可以表示为:
D ( X i , X j ) = m a x l ( ∣ x i l − x j l ∣ ) D(X_i,X_j)=max_l(|x_{il}-x_{jl}|) D(Xi,Xj)=maxl(∣xil−xjl∣)
此公式的另一种表示形式为:
D ( X i , X j ) = lim p → + ∞ ∑ l = 1 d ( x i l − x j l ) 2 p D(X_i,X_j)=\lim_{p\rightarrow+\infty}\sqrt[p]{\sum_{l=1}^d(x_{il}-x_{jl})^2} D(Xi,Xj)=limp→+∞p∑l=1d(xil−xjl)2
3,曼哈顿距离
在城市生活中,只能沿着街道从一个地方走到另一个地方,为此,人们将生活中熟悉的城市街区距离形象地称为曼哈顿距离。该距离的表示公式为:
D ( X i , X j ) = ∑ l = 1 d ( ∣ x i l − x j l ∣ ) D(X_i,X_j)=\sum_{l=1}^d(|x_{il}-x_{jl}|) D(Xi,Xj)=∑l=1d(∣xil−xjl∣)
曼哈顿距离在基于自适应谐振理论的同步聚类中有较好的应用;但是需要注意的是这种距离不再符合在特征空间中的转化和旋转的不变性。
4,闵可夫斯基距离
闵可夫斯基距离是一种p范数的形式,公式可以表示为:
D ( X i , X j ) = ∑ l = 1 d ( x i l − x j l ) 2 p D(X_i,X_j)=\sqrt[p]{\sum_{l=1}^d(x_{il}-x_{jl})^2} D(Xi,Xj)=p∑l=1d(xil−xjl)2
从式中可以看出,若p为无穷大时,这种距离可以称为切比雪夫距离;若p=2时就是欧几里得距离;那么当p=1时就是曼哈顿距离。
5,马氏距离
马氏距离是一种关于协方差矩阵的距离度量表示方法,其公式为:
D ( X i , X j ) = ( X i − X j ) T S − 1 ( X i − X j ) D(X_i,X_j)=\sqrt{(X_i-X_j)^TS^{-1}(X_i-X_j)} D(Xi,Xj)=(Xi−Xj)TS−1(Xi−Xj)
其中T表示转置,S为样本协方差矩阵。马氏距离的优点是距离与属性的量纲无关,并排除了属性之间的相关性干扰,若各个属性之间独立同分布,则协方差矩阵为单位矩阵。这样,平方马氏距离也就转化成了欧氏距离。
6,对称点距离
当聚类存在对称模式时,就可以使用对称点距离。其距离公式为:
D ( X i , X r ) = m a x j = 1 , 2 , … , N , j ≠ i ∣ ∣ ( X i − X r ) + ( X j − X r ) ∣ ∣ ∣ ∣ ( X i − X r ) ∣ ∣ + ∣ ∣ ( X j − X r ) ∣ ∣ D(X_i,X_r)=max_{j=1,2,…,N,j≠i}\frac{||(X_i-X_r)+(X_j-X_r)||}{||(X_i-X_r)||+||(X_j-X_r)||} D(Xi,Xr)=maxj=1,2,…,N,j=i∣∣(Xi−Xr)∣∣+∣∣(Xj−Xr)∣∣∣∣(Xi−Xr)+(Xj−Xr)∣∣
对称点距离就是该点到对称点和其他点距离的最小值。
7,相关系数
距离度量也可以源于相关系数,如皮尔逊相关系数的定义为:
ρ x i x j = C o v ( X i , X j ) D ( X i ) D ( X j ) ρ_{x_ix_j}=\frac{Cov(X_i,X_j)}{\sqrt{D(X_i)}\sqrt{D(X_j)}} ρxixj=D(Xi)D(Xj)Cov(Xi,Xj)
8,余弦相似度
最后一种直接计算相似性的方法是余弦相似度。其表示形式为:
S ( X i , X j ) = c o s α = X i T X j ∣ ∣ X i ∣ ∣ ∣ ∣ X j ∣ ∣ S(X_i,X_j)=cosα=\frac{X_i^TX_j}{||X_i||\ ||X_j||} S(Xi,Xj)=cosα=∣∣Xi∣∣ ∣∣Xj∣∣XiTXj
这里,S表示样本之间的相似性(以下同)。在特征空间中,两个样本越相似,则他们越趋向于平行,那么他们的余弦值也就越大。
(附:为什么大模型每个层之间要加入Layer Normalization?原因就是因为神经网络的基本计算就是点积相似度计算,而点积相似度的取值范围是没有约束的,这导致神经网络结构很难学习,因为variance太大了。所以引入Layer Normalization之后,可以让点积相似度变成了余弦相似度。当然中间有一个系数就是根号的输入向量的维度,这也就是为什么transformer架构中为什么要除以根号的输入向量的维度的原因,因为除以根号的输入向量的维度之后,Norm之后的向量,神经元的点积相似度就等于余弦相似度了。所以,让没有取值范围约束的点积相似度有了约束,【-1,1】,从而可以让神经网络稳定的训练。)
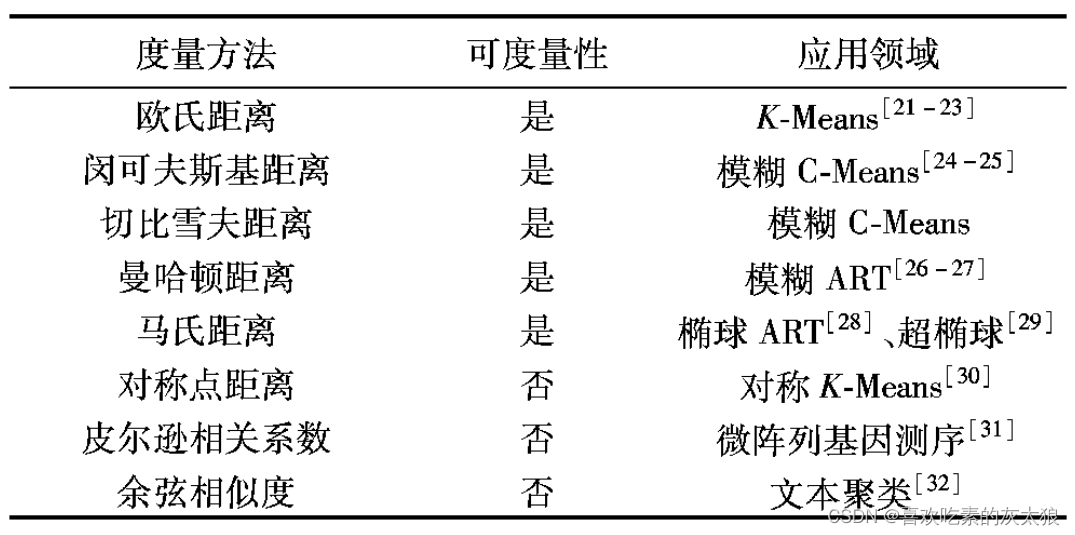
需要注意的是最后三类相似度计算方法不再符合对称性,非负性与反身性的要求,即属于非可度量的范畴。连续性变量的相似性度量方法在不同聚类算法中的应用如下图所示。
相关文章:

矩阵的相似性度量的常用方法
矩阵的相似性度量的常用方法 1,欧氏距离 欧式距离是最易于理解的一种距离计算方法,源自欧式空间中两点间的距离公式。 (1)二维平面上的点 a ( x 1 , y 1 ) a(x_1,y_1) a(x1,y1)和点 b ( x 2 , y 2 ) b(x_2,y_2) b(x2,y2)的欧式距离为 d ( x …...

Java之TCP,UDP综合小练习一
4. 综合练习 练习一:多发多收 需求: 客户端:多次发送数据 服务器:接收多次接收数据,并打印 代码示例: public class Client {public static void main(String[] args) throws IOException {//客户端&…...
Docker 日志管理 - ELK
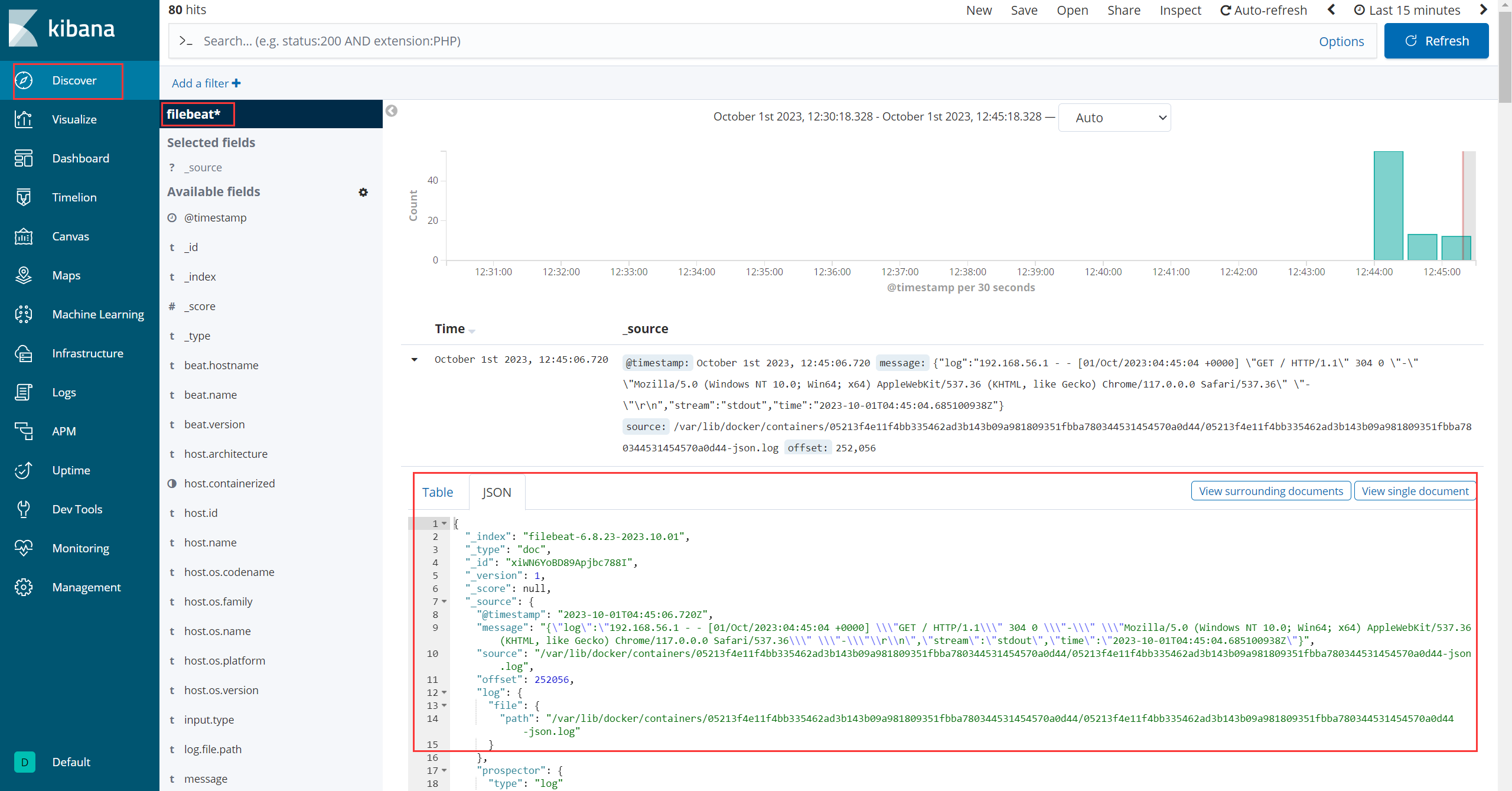
Author:rab 目录 前言一、Docker 日志驱动二、ELK 套件部署三、Docker 容器日志采集3.1 部署 Filebeat3.2 配置 Filebeat3.3 验证采集数据3.4 Kibana 数据展示3.4.1 创建索引模式3.4.2 Kibana 查看日志 总结 前言 如何查看/管理 Docker 运行容器的日志?…...
windows系统下利用python对指定文件夹下面的所有文件的创建时间进行修改
windows系统下利用python对指定文件夹下面的所有文件的创建时间进行修改 不知道其他的朋友们有没有这个需求哈,反正咱家是有这个需求 需求1、当前有大量的文件需要更改文件生成的时间,因为不可告知的原因,当前的文件创建时间是不能满足使用的…...

线性表的链式表示——单链表;头插,尾插,按值查找,按序号查找,插入,删除;
#include <iostream> #include <algorithm>//fill() #define InitSize 5using namespace std;/*线性表:链式表示——单链表;头插,尾插,按值查找,按序号查找,插入,删除*/ typedef st…...

【Spring Cloud系统】- Zookeer特性与使用场景
【Spring Cloud系统】- Zookeer特性与使用场景 一、概述 Zookeeper是一个分布式服务框架,是Apache Hadoop的一个子项目,它主要是用来解决分布式应用中经常遇到的一些数据管理问题。如:统一命名服务、状态同步服务、集群管理、分布式应用配置…...
最新AI智能创作系统源码SparkAi系统V2.6.3/AI绘画系统/支持GPT联网提问/支持Prompt应用/支持国内AI模型
一、智能AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统,已支持OpenAIGPT全模型国内AI全模型,已支持国内AI模型 百度文心一言、微软Azure、阿里云通义千问模型、清华智谱AIChatGLM、科大讯飞星火大模型等。本期针对源码…...
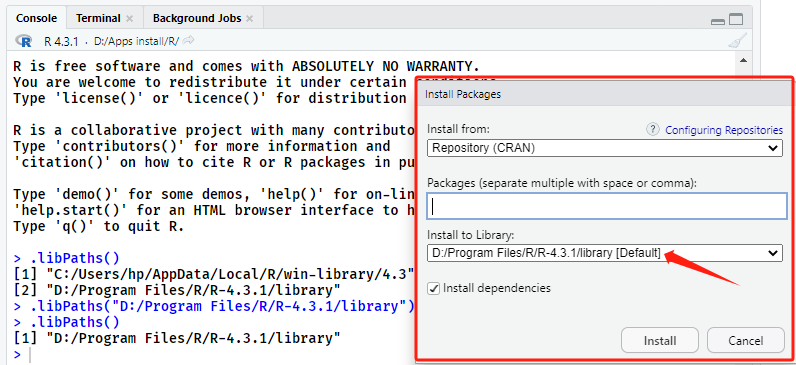
R | R包默认安装路径的查看及修改
R | R包默认安装路径的查看及修改 一、R包安装位置查看二、已安装R包查询三、R包安装位置修改四、R包安装位置永久修改 在【R: R package安装的几种方式】【R: R版本更新及R包迁移(详细步骤)】两篇文章中介绍过R包的常见安装方式,以及在不同R…...

将conda虚拟环境打包并集成到singularity镜像中
1. 使用yml文件打包 conda activate your_env conda env export > environment.yml编写cond.def文件 Bootstrap: dockerFrom: continuumio/miniconda3%filesenvironment.yml%post/opt/conda/bin/conda env create -f environment.yml%runscriptexec /opt/conda/envs/$(hea…...

Android Studio 是如何和我们的手机共享剪贴板的
背景 近期完成了target33的项目适配升级,随着AGP和gradle的版本升级,万年老版本Android Studio(后文简称AS)也顺便升级到了最新版Android Studio Giraffe | 2022.3.1,除了新UI外,最让我好奇的是这次的Running Devices功能(官方也称为Device mirroring)可以控制真机了. 按照操…...

大数据面试题:Spark和MapReduce之间的区别?各自优缺点?
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答: 1)spark和maprecude的对比;2)mapreduce与spark优劣好处 问过的一些公司:阿里云…...

【开发篇】十八、SpringBoot整合ActiveMQ
文章目录 1、安装ActiveMQ2、整合3、发送消息到队列4、使用消息监听器对消息队列监听5、流程性业务消息消费完转入下一个消息队列6、发布订阅模型 1、安装ActiveMQ docker安装 docker pull webcenter/activemqdocker run -d --name activemq -p 61616:61616 -p 8161:8161 webce…...

QTcpSocket 接收数据实时性问题
一、开发背景 使用 Qt 的 QTcpSocket 接收数据的时候发现数据接收出现粘包的现象,并且实时性很差,通过日志的时间戳发现数据接收的误差在 100ms 以内。 二、开发环境 Qt5.12.2 QtCreator4.8.2 三、实现步骤 在 socket 连接的槽函数设置接收延时时间&…...

前端el-select 单选和多选
el-select单选 <el-form-item label"部门名称" prop"departId"><el-select v-model"dataForm.departId" placeholder"请选择" clearable:style{ "width": "100%" } :multiple"false" filtera…...
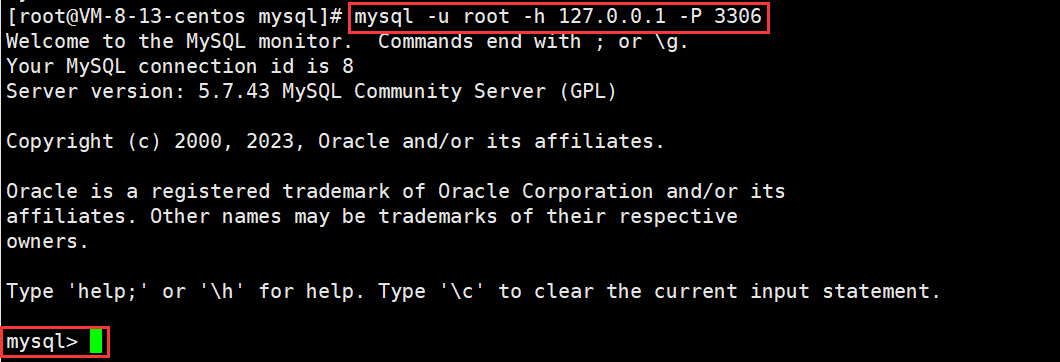
【MySQL】Linux 中 MySQL 环境的安装与卸载
文章目录 Linux 中 MySQL 环境的卸载Linux 中 MySQL 环境的安装 Linux 中 MySQL 环境的卸载 在安装 MySQL 前,我们需要先将系统中以前的环境给卸载掉。 1、查看以前系统中安装的 MySQL rpm -qa | grep mysql2、卸载这些 MySQL rpm -qa | grep mysql | args yum …...
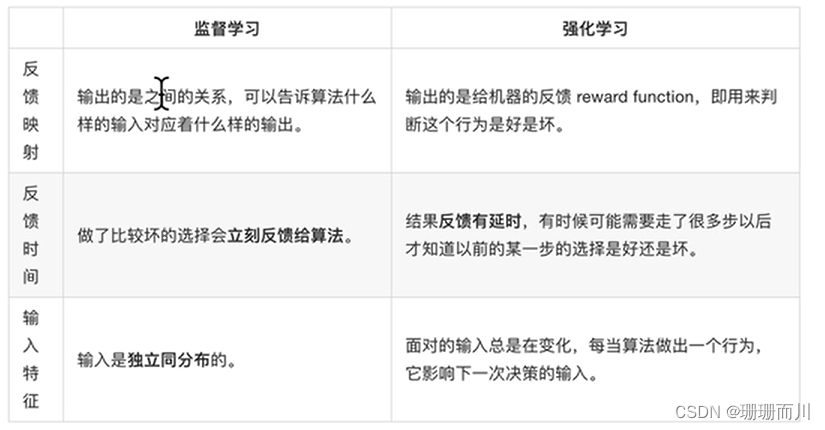
机器学习算法分类
学习视频黑马程序员 监督学习 无监督学习 半监督学习 强化学习...

Mysql bin-log日志恢复数据与物理备份-xtrabackup
主打一个数据备份与恢复 binlog与xtarbackup bin-log日志恢复开启bin-log配置bin-log日志恢复 物理备份-xtrabackup三种备份方式安装xtrabackup备份全量备份增量备份差异备份 bin-log日志恢复 bin-log 日志,就记录对数据库进行的操作,什么增删改的操作全…...
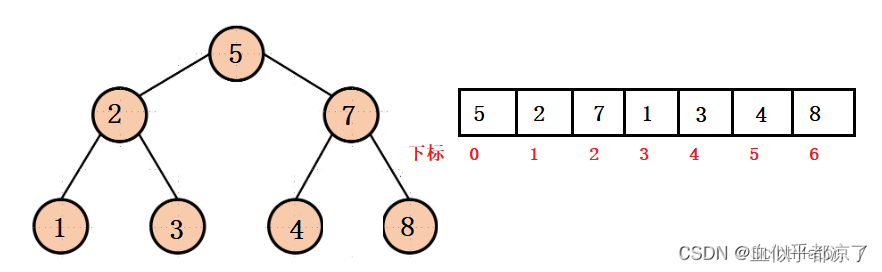
JAVA 学习笔记 2年经验
文章目录 基础String、StringBuffer、StringBuilder的区别jvm堆和栈的区别垃圾回收标记阶段清除阶段 异常类型双亲委派机制hashmap和hashtable concurrentHashMap 1.7和1.8的区别java的数据结构排序算法,查找算法堆排序 ThreadLocal单例模式常量池synchronizedsynch…...
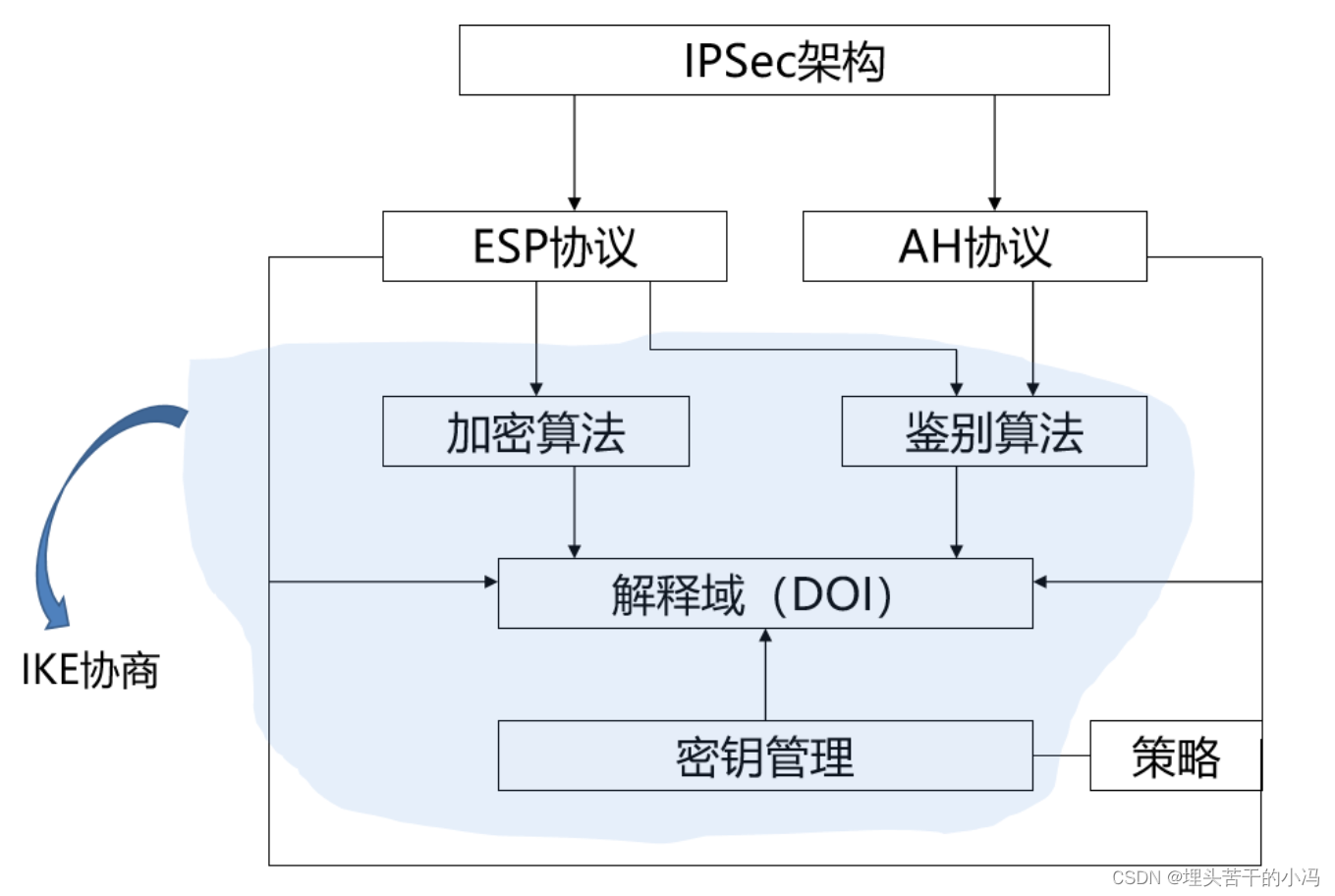
网络安全--安全认证、IPSEC技术
目录 1. 什么是数据认证,有什么作用,有哪些实现的技术手段? 2. 什么是身份认证,有什么作用,有哪些实现的技术手段? 3. 什么是VPN技术? 4. VPN技术有哪些分类? 5. IPSEC技术能够…...

Mysql——创建数据库,对表的创建及字段定义、数据录入、字段增加及删除、重命名表。
一.创建数据库 create database db_classics default charsetutf8mb4;//创建数据库 use db_classics;//使用该数据库二.对表的创建及字段定义 create table if not exists t_hero ( id int primary key auto_increment, Name varchar(100) not null unique, Nickname varchar(1…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
