【C++ 学习 ㉖】- 位图详解(哈希扩展)
目录
一、位图的概念
二、位图的实现
2.1 - bitset.h
2.2 - test.cpp
三、位图的应用
3.1 - 例题一
3.2 - 例题二
一、位图的概念
假设有这样一个需求:在 100 亿个整型数字中快速查询某个数是否存在其中,并假设是 32 位操作系统,4 GB 内存。
由于数字的数量如此之多,如果使用一个 int 型的数组进行存储,需要占用的内存空间为 ,那么如何用更小的空间来 "存储" 这些数字呢?
我们可以用比特位(bit)来标记数字,每个比特位中存放的值则表示其标记的数字是否存在,0 表示不存在,1 表示存在,这就是位图的基本思想。
例如,标记数字 1、2、4、6:

由于 int 总共有 种取值,所以标记所有这些数字需要占用的内存空间为
。
二、位图的实现
2.1 - bitset.h
#pragma once
#include <vector>
namespace yzz
{template<size_t N> // 总共有 N + 1 个比特位class bitset{public:bitset() : _v(N / 32 + 1) { }
void set(size_t x){size_t i = x / 32;size_t j = x % 32;_v[i] |= (1 << j);}
void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_v[i] &= ~(1 << j);}
bool test(size_t x) const{size_t i = x / 32;size_t j = x % 32;return _v[i] & (1 << j);}private:std::vector<int> _v;};
}2.2 - test.cpp
#include "bitset.h"
#include <iostream>
using namespace std;
int main()
{int arr[] = { -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 };yzz::bitset<0xffffffff> bs;for (const int& e : arr){bs.set(e);}bs.reset(-3);bs.reset(3);for (const int& e : arr){if (bs.test(e))cout << e << " ";}// -5 -4 -2 -1 0 1 2 4 5cout << endl;return 0;
}三、位图的应用
位图的应用是大量数据的快速排序、查找和去重。
3.1 - 例题一
给定 100 亿个整数,找到只出现一次的所有整数。
doublebitset.h:
#pragma once
#include "bitset.h"
namespace yzz
{template<size_t N>class doublebitset{public:void set(size_t x){if (_bs1.test(x) == 0 && _bs2.test(x) == 0) // 00 -> 01{_bs2.set(x);}else if (_bs1.test(x) == 0 && _bs2.test(x) == 1) // 01 -> 10{_bs1.set(x);_bs2.reset(x);}// 10 则不变}
bool isSingleNum(size_t x) const{return _bs1.test(x) == 0 && _bs2.test(x) == 1;}private:bitset<N> _bs1;bitset<N> _bs2;};
}
思路:用 2 个比特位来表示一个数字的状态,00 表示不存在,01 表示只出现一次,10 表示出现一次以上。
具体实现则是使用两个位图。
思考:给定 100 亿个整数,找到出现次数不超过 2 次的所有整数。
思路是类似的,用 2 个比特位来表示一个数字的状态,00 表示不存在,01 表示只出现一次,10 表示出现两次,11 表示出现两次以上。
test.cpp:
#include "doublebitset.h"
#include <iostream>
using namespace std;
int main()
{int arr[] = { -3, -3, -2, -1, -2, 0, 1, 1, 2, 2, 3 };yzz::doublebitset<0xffffffff> dbs;for (const int& e : arr){dbs.set(e);}for (const int& e : arr){if (dbs.isSingleNum(e))cout << e << " ";}// -1 0 3cout << endl;return 0;
}3.2 - 例题二
给两个文件,分别有 100 亿个整数,求两个文件的交集。
法一:
#include "bitset.h"
#include <iostream>
using namespace std;
int main()
{int arr1[] = { -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 };int arr2[] = { -3, -3, -2, -1, -2, 0, 1, 1, 2, 2, 3 };yzz::bitset<0xffffffff> bs1;yzz::bitset<0xffffffff> bs2;// 去重for (const int& e : arr1){bs1.set(e);}for (const int& e : arr2){bs2.set(e);}// 求交集for (int i = -10; i <= 10; ++i){if (bs1.test(i) && bs2.test(i))cout << i << " ";}// -3 -2 -1 0 1 2 3cout << endl;return 0;
}法二:
#include "bitset.h"
#include <iostream>
using namespace std;
int main()
{int arr1[] = { -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 };int arr2[] = { -3, -3, -2, -1, -2, 0, 1, 1, 2, 2, 3 };yzz::bitset<0xffffffff> bs;for (const int& e : arr1){bs.set(e);}for (const int& e : arr2){if (bs.test(e)){cout << e << " ";bs.reset(e); // 避免出现重复的数字}}// -3 -2 -1 0 1 2 3cout << endl;return 0;
}相关文章:
【C++ 学习 ㉖】- 位图详解(哈希扩展)
目录 一、位图的概念 二、位图的实现 2.1 - bitset.h 2.2 - test.cpp 三、位图的应用 3.1 - 例题一 3.2 - 例题二 一、位图的概念 假设有这样一个需求:在 100 亿个整型数字中快速查询某个数是否存在其中,并假设是 32 位操作系统,4 GB…...

天启科技联创郭志强:趟遍教育行业信数化沟坎,创业智能赛道重塑行业生态
郭志强 天启科技联合创始人 近20年互联网、企业信息化、数字化实施、管理及培训经验。对于集团型企业及初创企业、传统企业及互联网企业的信息化、数字化转型有自己独到的见解和实操经验。具备跨区域、集团化信息规划、解决方案、系统架构及企业流程搭建、优化和技术团队管理能…...
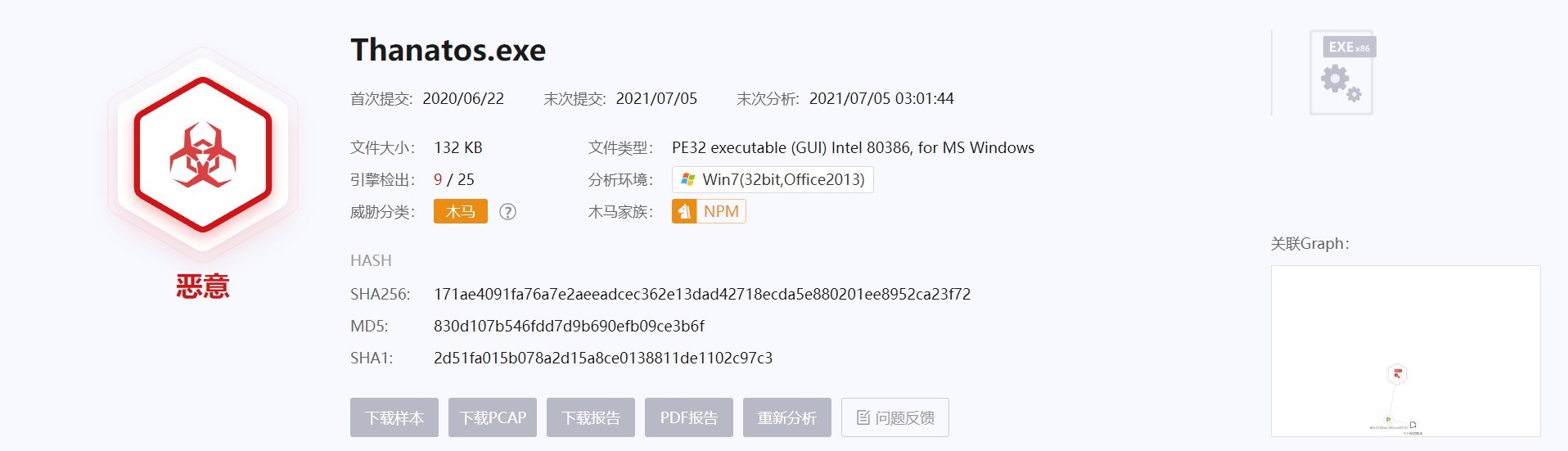
Cuckoo沙箱各Ubuntu版本安装及使用
1.沙箱简介 1.1 沙箱 沙箱是一个虚拟系统程序,允许你在沙箱环境中运行浏览器或其他程序,因此运行所产生的变化可以随后删除。它创造了一个类似沙盒的独立作业环境,在其内部运行的程序并不能对硬盘产生永久性的影响。 在网络安全中ÿ…...

什么是mvvm模式,优点是什么
MVVM(Model-View-ViewModel)模式是一种设计模式。它是一种开发模式,旨在分离用户界面的开发和业务逻辑的开发。MVVM模式将应用程序分为三个部分: Model:它代表应用程序的数据模型和业务逻辑。 View:它代表…...

C/C++ 中的函数返回局部变量以及局部变量的地址?
C/C中,函数内部的一切变量(函数内部局部变量,形参)都是在其被调用时才被分配内存单元。形参和函数内部的局部变量的生命期和作用域都是在函数内部(static变量的生命期除外)。子函数运行结束时,所有局部变量的内存单元会被系统释放。在C中&…...
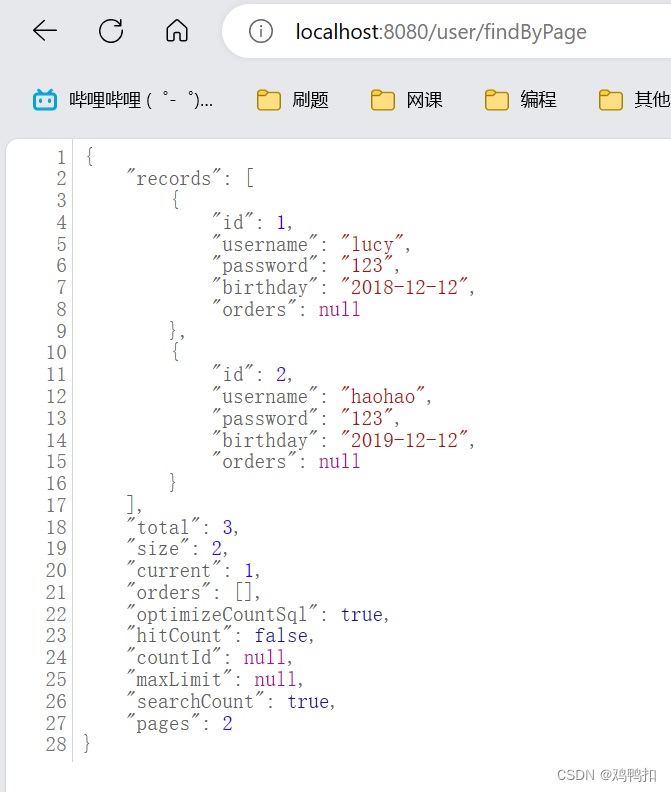
springboot和vue:七、mybatis/mybatisplus多表查询+分页查询
mybatisplus实际上只对单表查询做了增强(速度会更快),从传统的手写sql语句,自己做映射,变为封装好的QueryWrapper。 本篇文章的内容是有两张表,分别是用户表和订单表,在不直接在数据库做表连接的…...
【Leetcode】 51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。 每一种…...

Java数据库连接:JDBC介绍与简单示例
Java数据库连接:JDBC介绍与简单示例 在Java程序中,操作数据库是必不可少的。JDBC(Java Database Connectivity)是Java中用于连接和操作数据库的一种技术。通过JDBC,Java程序可以与各种关系型数据库进行交互࿰…...

智慧茶园:茶厂茶园监管可视化视频管理系统解决方案
一、方案背景 我国是茶叶生产大国,茶叶销量全世界第一。随着经济社会的发展和人民生活水平的提高,对健康、天然的茶叶产品的消费需求量也在逐步提高。茶叶的种植、生产和制作过程工序复杂,伴随着人力成本的上升,传统茶厂的运营及…...
springboot整合pi支付开发
pi支付流程图: 使用Pi SDK功能发起支付由 Pi SDK 自动调用的回调函数(让您的应用服务器知道它需要发出批准 API 请求)从您的应用程序服务器到 Pi 服务器的 API 请求以批准付款(让 Pi 服务器知道您知道此付款)Pi浏览器向…...
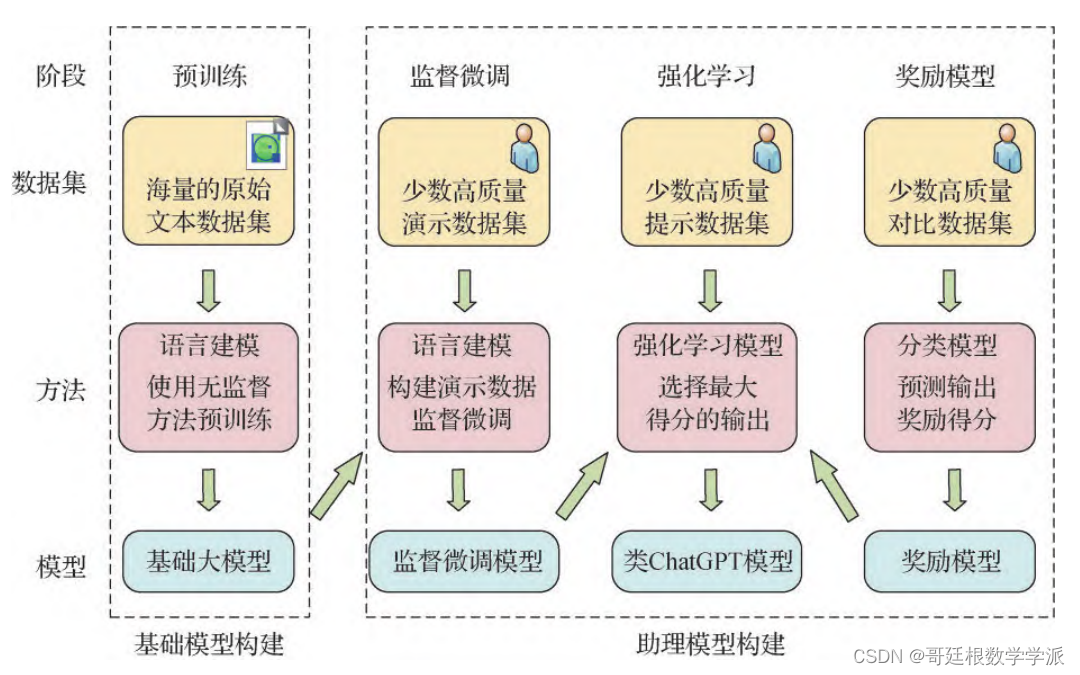
类 ChatGPT 模型存在的局限性
尽管类ChatGPT模型经过数月的迭代和完善,已经初步融入了部分领域以及人们的日常生活,但目前市面上的产品和相关技术仍然存在一些问题,以下列出一些局限性进行详细说明与成因分析: 1)互联网上高质量、大规模、经过清洗…...

Nginx的安全控制
安全控制 关于web服务器的安全是比较大的一个话题,里面所涉及的内容很多,Nginx反向代理是安全隔离来提升web服务器的安全,通过代理分开了客户端到应用程序服务器端的连接,实现了安全措施。在反向代理之前设置防火墙,…...

字符串与字符编码 - GO语言从入门到实战
字符串与字符编码 - GO语言从入门到实战 字符串 与其他主要编程语⾔的差异 基本数据类型:string 是基础数据类型,而不是引用类型或指针类型。string 在内存中占用的空间大小是固定的,且只读、不可改变。字节切片:string 是只读…...

12P4375X042-233C KJ2005X1-BA1 CE3007 EMERSON servo controller
12P4375X042-233C KJ2005X1-BA1 CE3007 EMERSON servo controller 我们提供三种不同类别的EDGEBoost I/O模块供选择,以实现最大程度的I/O定制: 数字和模拟输入/输出网络和连接边缘人工智能和存储 利用EDGEBoost I/O实现变革性技术 EBIO-2M2BK EBIO-2M2BK载板支持…...
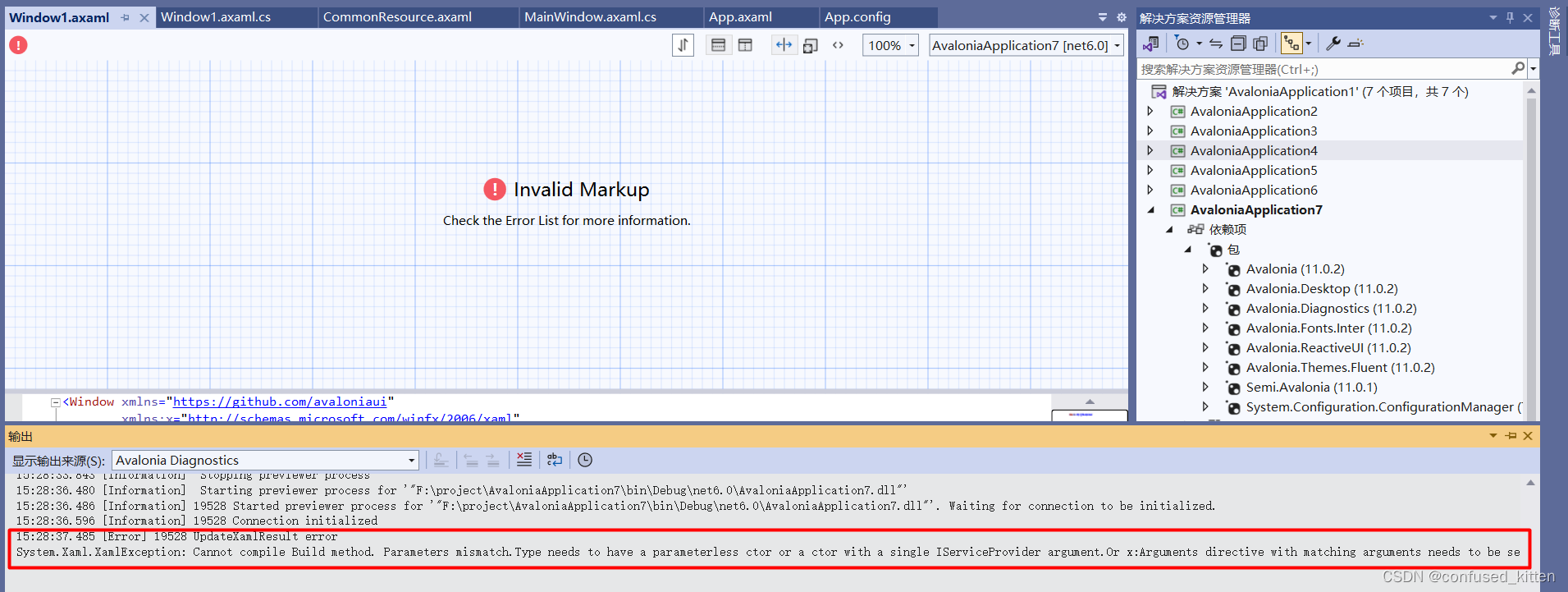
WPF向Avalonia迁移(四、其他事项)
开发必备 1. Avalonia项目源代码!!!!!!!!!!没有源代码,你连控件的背景色怎么改都找不着!! 2.下载你所使用的版本&#x…...

Python 代码调试
from pdb import set_trace as stx 是一个Python代码中常用的调试技巧之一,它用于在代码中插入断点以进行调试。这行代码的作用是将Python标准库中的 pdb(Python Debugger)模块中的 set_trace 函数导入,并将其重命名为 stx&#x…...
DM宣传单制作,利用在线模板,快速替换文字
如果你需要制作一批宣传单,但是时间很紧,而且没有专业的设计人员协助,那么你可以选择使用在线模板来快速制作宣传单。本文将介绍如何使用乔拓云平台,快速制作宣传单的方法。 步骤一:选择适合的在线制作工具 首先&…...
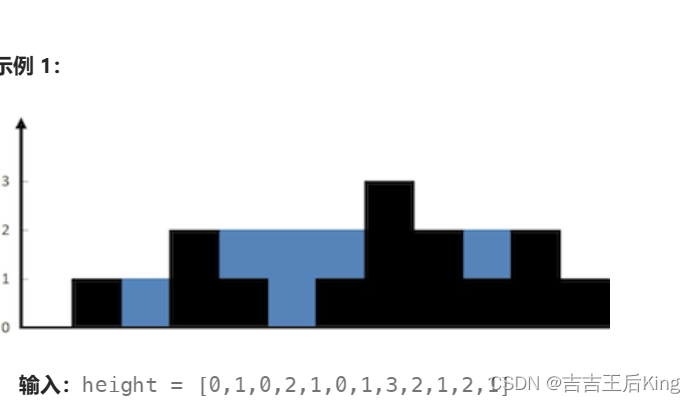
【力扣】42. 接雨水
这道题我卡了差不多1个小时,不是不会做,是不知道怎么能用栈来实现,后面看了一个博主的视频,豁然开朗,我主要的纠结点在于当指针指到7的时候,我计算出4到7的水块是2,但实际上是0,因为…...
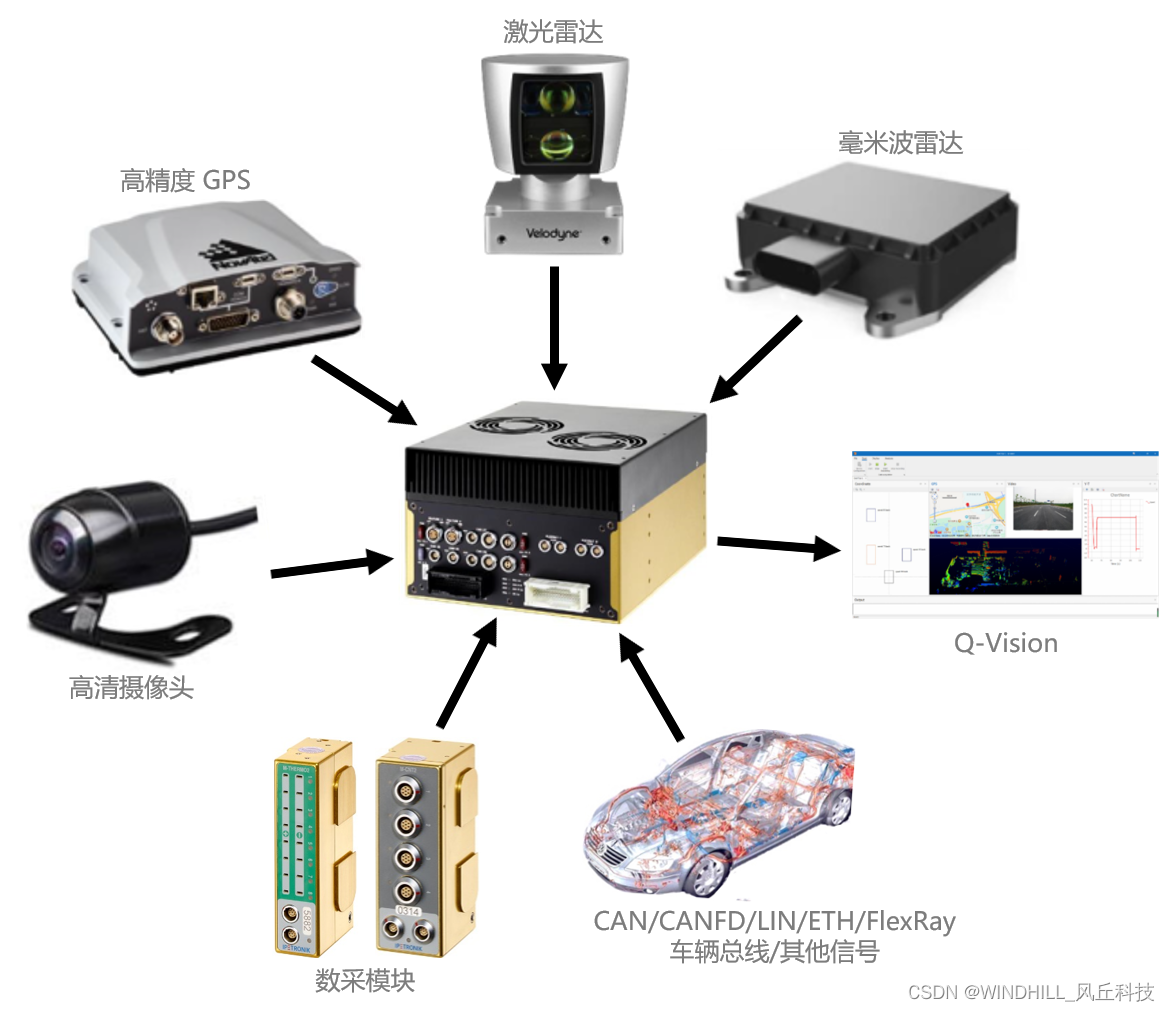
IPETRONIK数据采集设备携手Softing Q-Vision软件致力于ADAS测试方案
一 背景 汽车ADAS技术是当下国内外的重点研究方向,且ADAS的发展水平和市场竞争力紧密相关,因此一套完善的ADAS测试方案对各整车厂而言非常重要。然而,国内ADAS测试却面临着很多阻碍,主要原因在于:相关测试设备昂贵&am…...
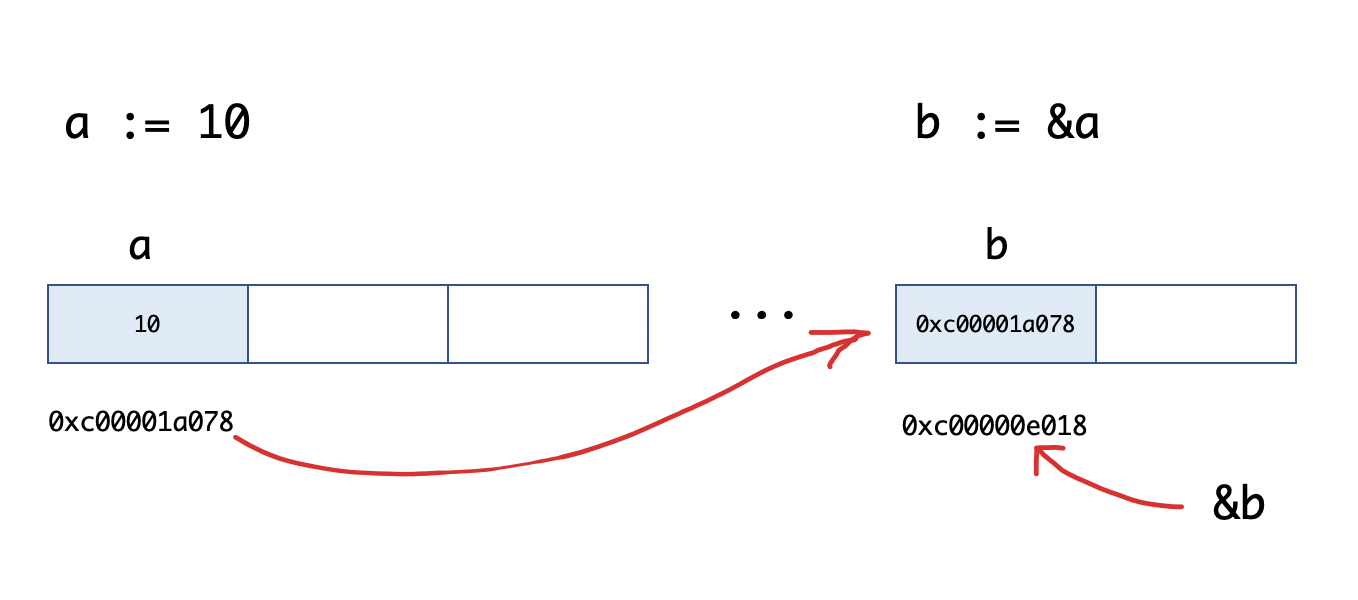
Go语言中的指针介绍
Go语言中的指针 文章目录 Go语言中的指针一、Go语言中的指针介绍1.1 指针介绍1.2 基本语法1.3 声明和初始化1.4 Go 指针的3个重要概念1.4.1 指针地址(Pointer Address)1.4.2 指针类型(Pointer Type)1.4.3 指针取值(Poi…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
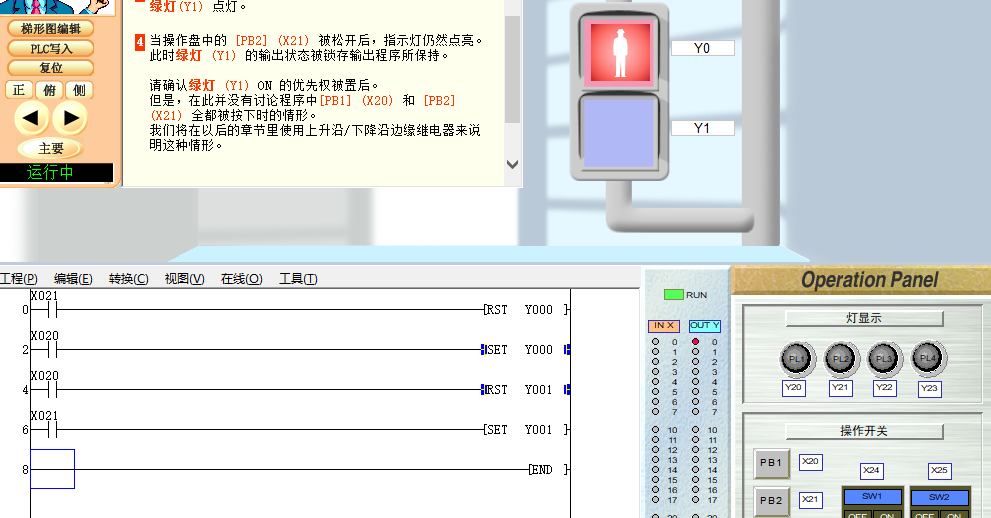
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...
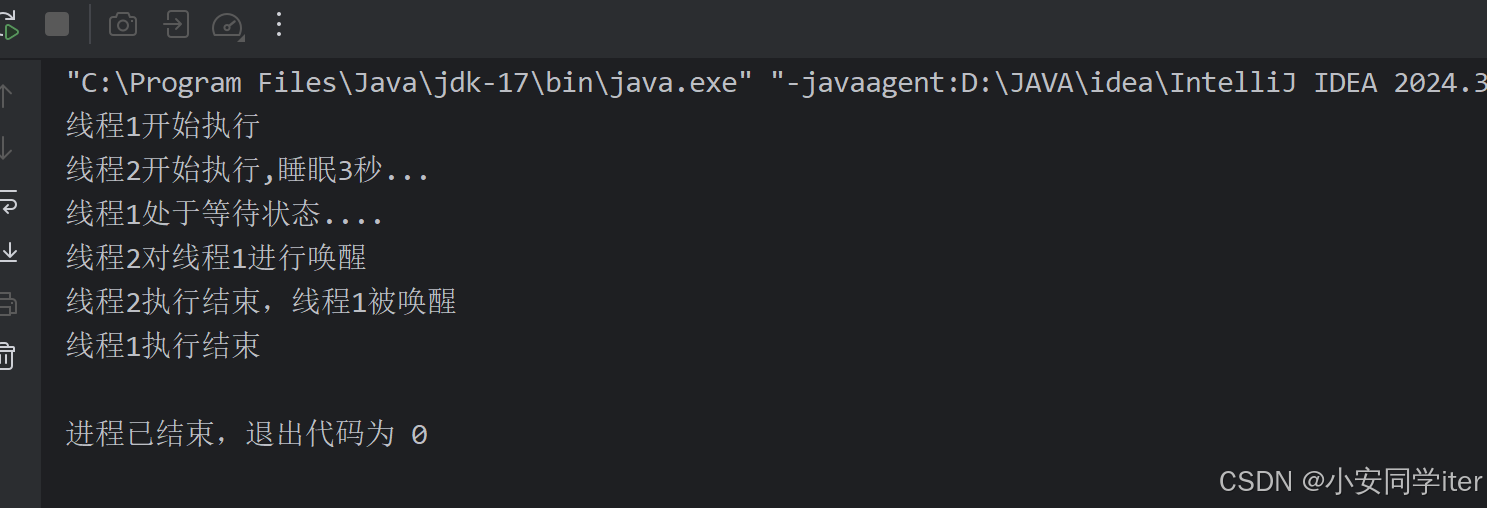
JUC并发编程(二)Monitor/自旋/轻量级/锁膨胀/wait/notify/锁消除
目录 一 基础 1 概念 2 卖票问题 3 转账问题 二 锁机制与优化策略 0 Monitor 1 轻量级锁 2 锁膨胀 3 自旋 4 偏向锁 5 锁消除 6 wait /notify 7 sleep与wait的对比 8 join原理 一 基础 1 概念 临界区 一段代码块内如果存在对共享资源的多线程读写操作…...
