【数据结构】快排的详细讲解
目录:
介绍
一,递归快排确定基准值
二,递归遍历
三,非递归的快排
四,快排的效率
介绍
快排是排序算法中效率是比较高的,快排的基本思想是运用二分思想,与二叉树的前序遍历类似,将数据划分,每次划分确定1个基准值(就是已经确定好有序后位置的数据),以升序为例,基准值左面的数据都比此值小,右面的数据都比此值大,然后以基准值为分界线,经过不断划分,最终基准值的个数达到n,数据即有序,因此,递归运用是不二选法,也可运用非递归,但是比较麻烦。
一,递归快排确定基准值
确定基准值的方法常用的有三种,普通法,挖坑法,前后指针法。
1,普通法,具体思想图如下(以升序为例):

上面说过,基准值的确定过程要保证左面的数据都比此值小或大,右面的数据都要比此值大或小,因此,此基准值就确定了在整个数据中的位置。以升序为例,我们可以从开头和末尾遍历数据,比开头(以首元素为基准)元素大的放在最后,比开头元素小的数据放在前面,最终当两者相遇后再与开头元素交换即可确定基准值(注意:此步骤有细节,具体后面会说明)。如下图:
基准值过程图

现在有个注意要素套提一下,当上图中的前面L和后面R相遇时,如何保证此值一定比首元素小呢?这里我们需要控制好L的走向即可,即让R先走,当遇见比首元素小时退出,然后让L走,最后让两者进行交换,这样一来无论出现什么情况,当L与R相遇时对应的数据将一定比首元素(即以第一个元素为基准)小,此步骤称为预排序。
基准值的确定代码如下:
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}int PartSort1(int* a, int begin, int end) {
int key = begin;
while (begin < end) {
//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),
//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.
while (begin < end && a[end] >= a[key]) {
end--;
}
//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小
while (begin < end && a[begin] <= a[key]) {
begin++;
}
Swap(a + end, a + begin);
}
Swap(a + key, a + begin);
return begin;
}
2,挖坑法,原理图如下(以升序为例):
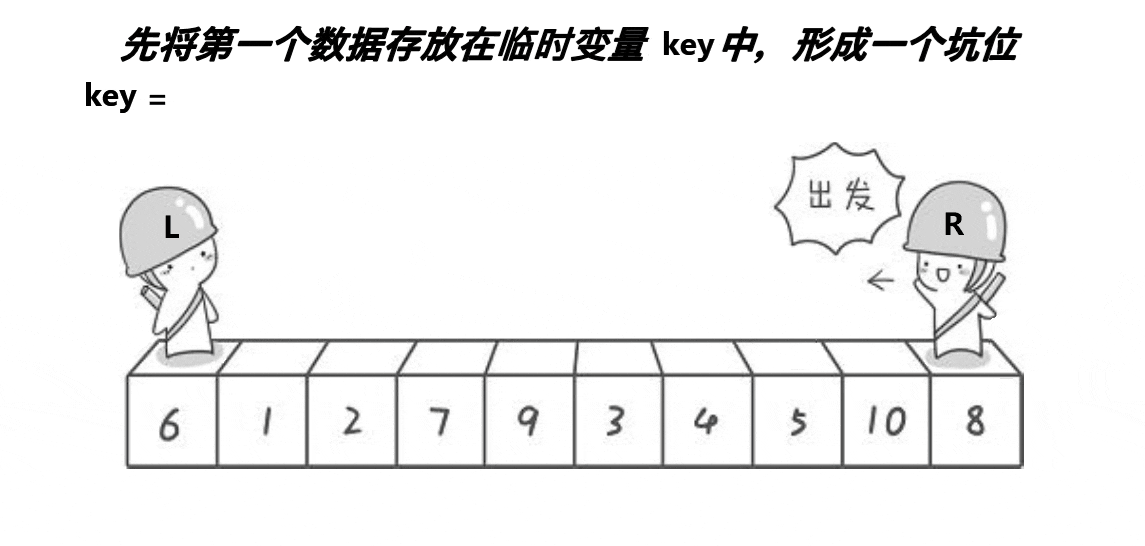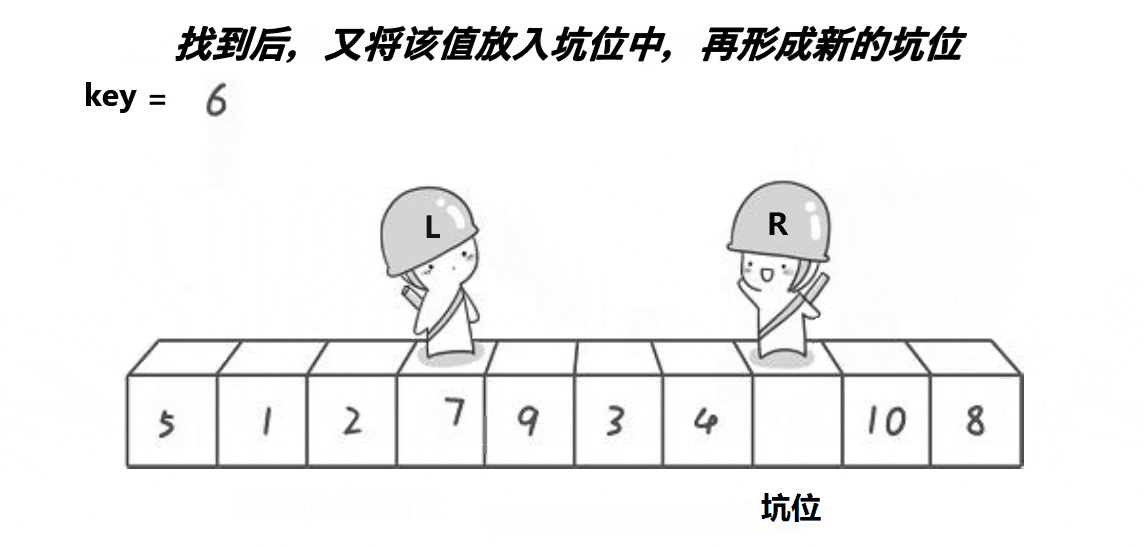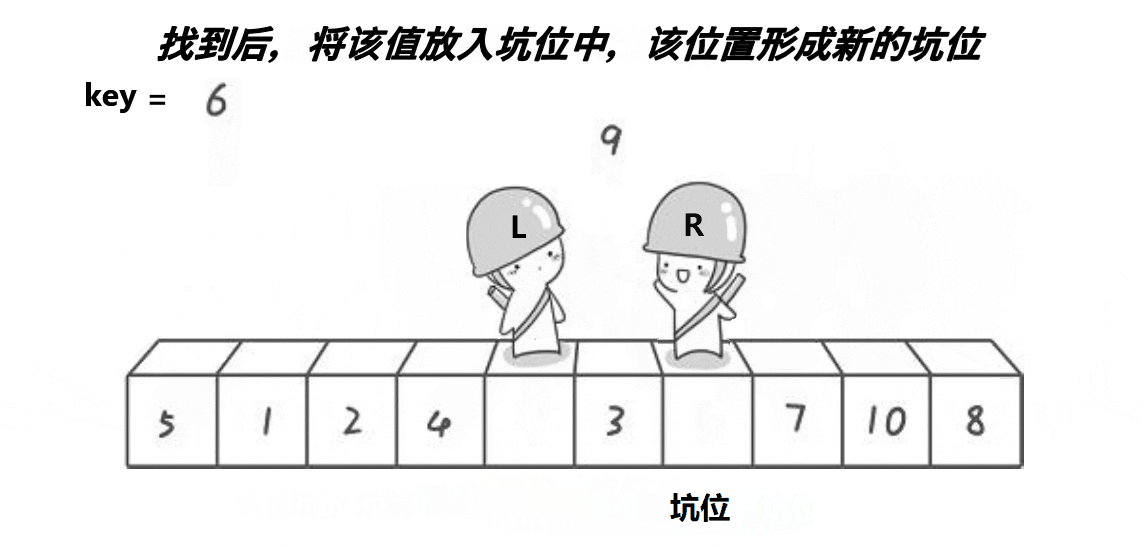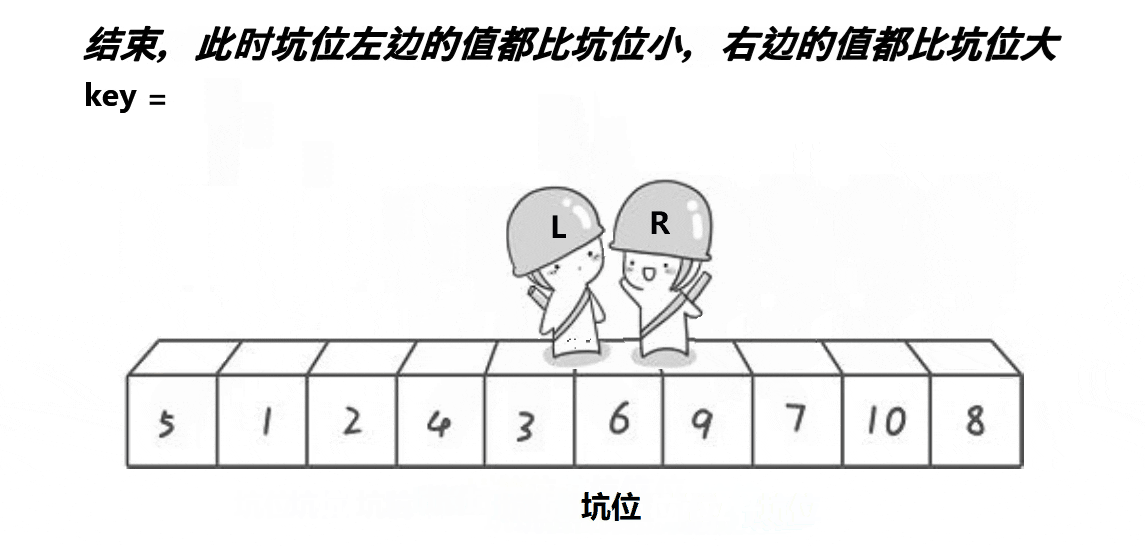
挖坑发大致思想与普通法一样,不同的是挖坑发有了坑位。挖坑发是先将首元素保存,将此位置形成坑位(其实坑位上有数据,但坑位的数据不影响,为了方便理解,所以在上图中的坑位就没写上去),然后开始首尾遍历(尾要先遍历,原理同上),比key大的元素放在后面,比key小的元素放在前面,一旦不满足此情况,这个数据将给到位置L或位置R,原本的位置将会形成坑位,直到两者相遇为止,结束遍历,最后把key的值放入坑位即可。代码如下:
int PartSort2(int* a, int begin, int end) {
int key = a[begin];
int hole = begin;//开头先形成坑位
while (begin < end) {
// 右边先走(原理与PartSort1原理一样),找小,填到左边的坑,右边形成新的坑位
while (begin < end && a[end] >= key) {
end--;
}
a[hole] = a[end];
hole = end;
// 左边再走,找大,填到右边的坑,左边形成新的坑位
while (begin < end && a[begin] <= key) {
begin++;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
3,前后指针法(prev是前指针,cur是后指针,此指针是位置指针,不是我们所常说的指针型),原理图如下:
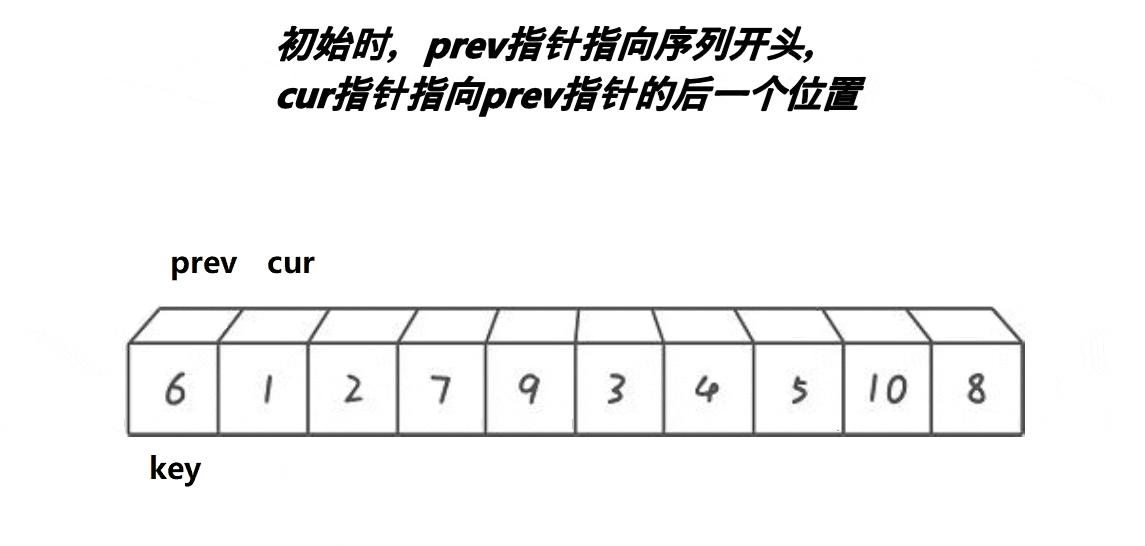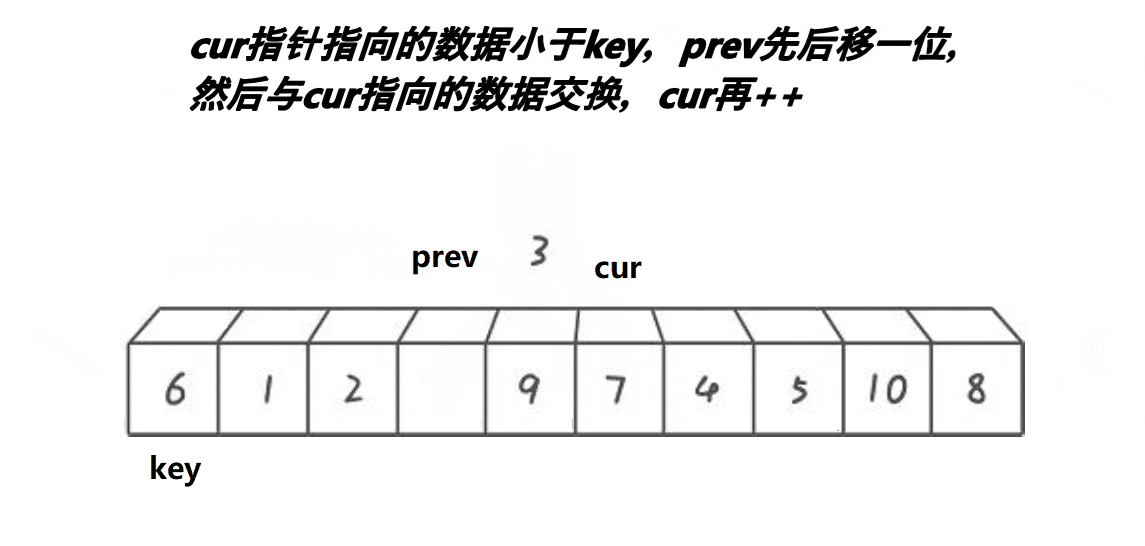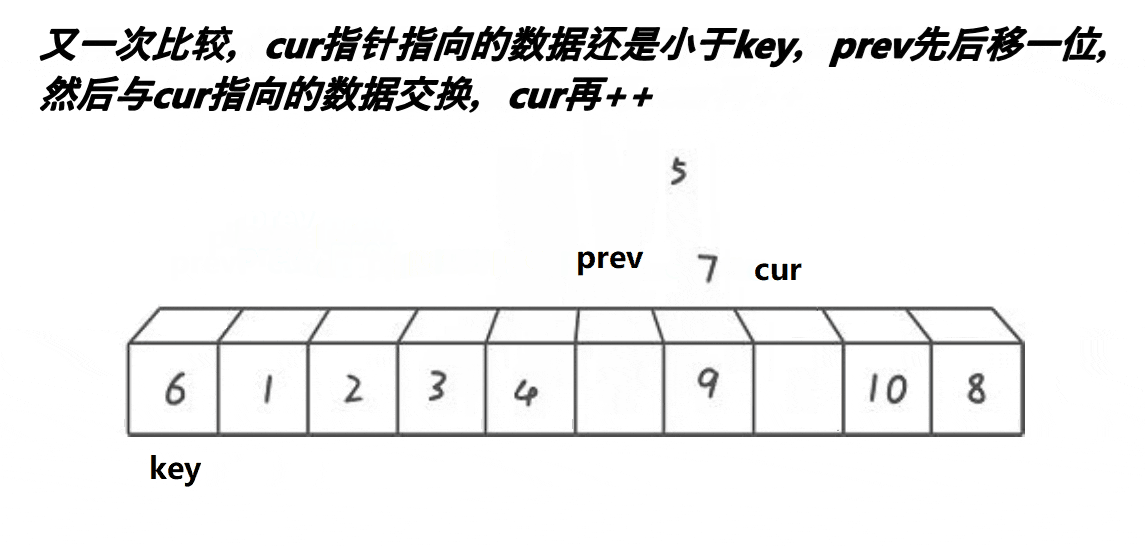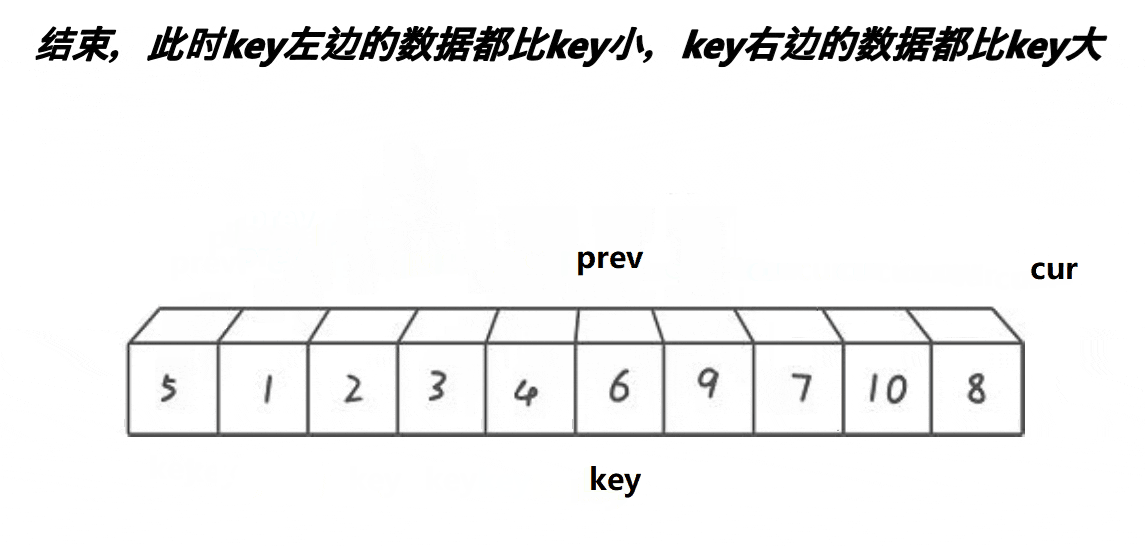
前后指针法跟上面两种方法有很大不同,如上,以第一个元素为基准,即定义key值为首元素,cur往前遍历,prev随之跟上cur的步伐,当prev遇到的数据比key小,prve向前移动;当prev遇到的数据比key大,prev停止移动,此时,cur不断向前移动,一旦找到比key小的数据就会跟prev指向的数据进行交换,最后,当cur遍历完整个数据后cur与key会进行交换,确定此时key所对应的值比左边数据大,比右边数据小。代码如下:
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}
int PartSort3(int* a, int begin, int end) {
int front = begin + 1;
int back = begin;
while (front <= end) {
if (a[front] <= a[begin]) {
back++;
Swap(a + back, a + front);
}
front++;
}
//因为后指针控制,所以当程序结束后back所指向的数据都比keyi所指向的数据小
Swap(a + begin, a + back);
return back;
}
总:以上三种遍历确定基准值的方法在快排称为预排序,每一趟预排序都可确定数据中一个元素的排序位置,每当确定一个数据后相对位置后,我们只需要不断以上次遍历时确定的基准值为界,递归遍历数据,即可确定最终确定序列。
二,递归遍历
当我们明白如何确定基准值后,接下来就是程序的结构搭建了,上面说过,快排递归跟二叉树的前序遍历一样,并且还需要以基准值为分界线,不断确定基准值,具体思路导图如下:

当确定好基准值key后,以区间[begin, key - 1]和区间[key + 1, end]进行划分(begin是要进行遍历时,开头元素的坐标,end是要遍历时,结尾元素的坐标,如上图),以次区间不断进行与二叉树前序遍历相同的递归,根据上图所示,很明显,当begin>=end时结束下一层递归。代码如下:
void QuickSort(int* a, int begin, int end)
{
//即当不存在区间时结束,即就排好了一个数
if (begin >= end)
return;
//运用普通法PartSort1,此算法是返回一个顺序表中中间值的坐标,在坐标左边都小于此数,在坐标的右边都大于此数
int keyi = PartSort1(a, begin, end);//也可用挖坑法和前后指针法
// 区间递归: 以keyi为界,左[begin, keyi-1],右[keyi+1, end],一直缩小,最终会逐渐会缩小成有序
QuickSort(a, begin, keyi - 1);//在keyi的左面进行遍历
QuickSort(a, keyi + 1, end);//在keyi的右面进行遍历
}
下面是总代码:
#include <stdio.h>
void Swap(int* x1, int* x2) {int t = *x1;*x1 = *x2;*x2 = t;
}
int PartSort1(int* a, int begin, int end) {int key = begin;while (begin < end) {//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.while (begin < end && a[end] >= a[key]) {end--;}//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小while (begin < end && a[begin] <= a[key]) {begin++;}Swap(a + end, a + begin);}Swap(a + key, a + begin);return begin;
}
void QuickSort(int* a, int begin, int end)
{//即当不存在区间时结束,即就排好了一个数if (begin >= end)return;//PartSort1算法是返回一个顺序表中中间值的坐标,在坐标左边都小于此数,在坐标的右边都大于此数int keyi = PartSort1(a, begin, end);// 区间递归: 左[begin, keyi-1] keyi 右[keyi+1, end],一直缩小,最终会逐渐会缩小成排序QuickSort(a, begin, keyi - 1);//在keyi的左面进行遍历QuickSort(a, keyi + 1, end);//在keyi的右面进行遍历
}
void Print(int* a, int n) {for (int i = 0; i < n; i++) {fprintf(stdout, "%d ", a[i]);}puts("");
}
void TestQuickSort()
{int a[] = { 6,1,2,7,9,3,4,5,10,8 };QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);Print(a, sizeof(a) / sizeof(int));
}
int main() {TestQuickSort();return 0;
}运行图:
三,非递归的快排
运用非递归,大多数要运用栈结构,因为递归本身其实就是不断入栈和出栈,递归过程跟栈结构一样,进入递归就是入栈,出函数就是出栈,都是先进后出。快排的非递归实现,我们也可用栈来实现。根据前面递归的运用,递归是不断进行区间分割,我们可将此区间放入栈中,然后进行不断循环遍历,每当遍历时就将区间放入栈中,一旦用完此区间就释放,跟递归中函数栈帧的创建与销毁一样。非递归结构代码如下:
1,栈的建立
typedef struct stack {
int* Data;
int Capacity;
int Top;
}Stack;
//以下三个是要运用栈结构的算法
void StackInit(Stack* S);
void StackPop(Stack* S);
void StackPush(Stack* S, int X);
//栈功能的实现
void StackInit(Stack* S) {//初始化栈
assert(S);
S->Data = 0;
S->Capacity = 0;
S->Top = -1;
}
void StackPop(Stack* S) {//出栈
assert(S || S->Data || S->Top != -1);
S->Top--;
}
void StackPush(Stack* S, int X) {//入栈
assert(S);
if (!S->Data) {
S->Data = (int*)malloc(sizeof(int) * 4);
assert(S->Data);
S->Capacity = 4;
}
else if (S->Top == S->Capacity - 1) {
S->Data = (int*)realloc(S->Data, (sizeof(int) * S->Capacity) * 2);
assert(S->Data);
S->Capacity *= 2;
}
S->Data[++S->Top] = X;
}
2,非递归的结构
void QuickSort(int* a, int left, int right) {
//创建栈结构S,以栈来模仿递归过程
Stack* S = (Stack*)malloc(sizeof(Stack));
StackInit(S);
StackPush(S, right);
StackPush(S, left);
while (S->Top != -1) {
//确定左右区间,每当遍历完一次时要及时更换,即从栈中去除操作
int begin = S->Data[S->Top];
StackPop(S);
int end = S->Data[S->Top];
StackPop(S);
//用指定好的区间进行预排序,即一次遍历
int key = PartSort1(a, begin, end);
//进行左区间的遍历
if (end - 1 > begin) {
//注意栈结构先进后出的特点,要先把end装进去
StackPush(S, end - 1);
StackPush(S, begin);
}
//进行右区间的遍历
if (begin + 1 < end) {
//同理,要先把end装进去
StackPush(S, end);
StackPush(S, begin + 1);
}
}
free(S);
//注意,不能在此算法内这样写,因为这是的a是首元素地址,即指针,sizeof(a)为地址的大小
//Print(a, sizeof(a) / sizeof(int));
}
以上是非递归过程中的逻辑代码,除此两大步,其它的逻辑运用与递归无任何区别,总代码如下:
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
typedef struct stack {int* Data;int Capacity;int Top;
}Stack;//以下三个是要运用栈结构的算法
void StackInit(Stack* S);
void StackPop(Stack* S);
void StackPush(Stack* S, int X);
//栈功能的实现
void StackInit(Stack* S) {//初始化栈assert(S);S->Data = 0;S->Capacity = 0;S->Top = -1;
}
void StackPop(Stack* S) {//出栈assert(S || S->Data || S->Top != -1);S->Top--;
}
void StackPush(Stack* S, int X) {//入栈assert(S);if (!S->Data) {S->Data = (int*)malloc(sizeof(int) * 4);assert(S->Data);S->Capacity = 4;}else if (S->Top == S->Capacity - 1) {S->Data = (int*)realloc(S->Data, (sizeof(int) * S->Capacity) * 2);assert(S->Data);S->Capacity *= 2;}S->Data[++S->Top] = X;
}
void Swap(int* x1, int* x2) {int t = *x1;*x1 = *x2;*x2 = t;
}
int PartSort1(int* a, int begin, int end) {int key = begin;while (begin < end) {//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.while (begin < end && a[end] >= a[key]) {end--;}//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小while (begin < end && a[begin] <= a[key]) {begin++;}Swap(a + end, a + begin);}Swap(a + key, a + begin);return begin;
}
void QuickSort(int* a, int left, int right) {//创建栈结构S,以栈来模仿递归过程Stack* S = (Stack*)malloc(sizeof(Stack));StackInit(S);StackPush(S, right);StackPush(S, left);while (S->Top != -1) {//确定左右区间,每当遍历完一次时要及时更换,即从栈中去除操作int begin = S->Data[S->Top];StackPop(S);int end = S->Data[S->Top];StackPop(S);//用指定好的区间进行预排序,即一次遍历int key = PartSort1(a, begin, end);//进行左区间的遍历if (end - 1 > begin) {//注意栈结构先进后出的特点,要先把end装进去StackPush(S, end - 1);StackPush(S, begin);}//进行右区间的遍历if (begin + 1 < end) {//同理,要先把end装进去StackPush(S, end);StackPush(S, begin + 1);}}free(S);//注意,不能在此算法内这样写,因为这是的a是首元素地址,即指针,sizeof(a)为地址的大小//Print(a, sizeof(a) / sizeof(int));
}
void Print(int* a, int n) {for (int i = 0; i < n; i++) {fprintf(stdout, "%d ", a[i]);}puts("");
}
int main() {int a[] = { 0,5,7,9,3,4,1,6,2,8 };QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);Print(a, sizeof(a) / sizeof(int));return 0;
}运行图:
四,快排的效率
1,快排的效率分析
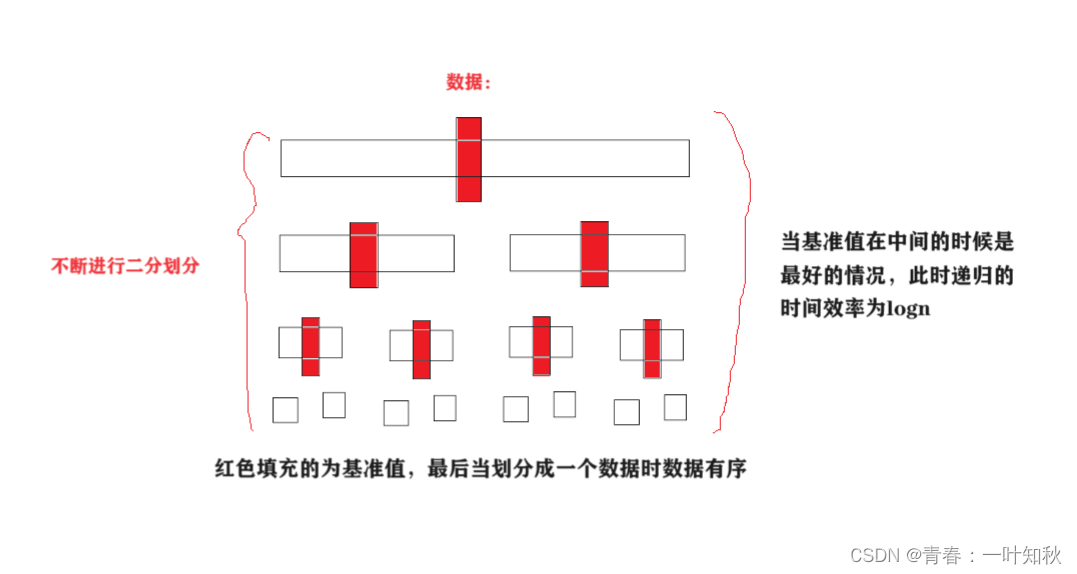
快排效率在平常说是效率比较高的,大致根据二叉树原理计算,快排时间复杂度为O(nlogn),空间复杂度为O(logn),但这只是对于大多时候,其实快排的时间效率是很不确定的,快排的效率跟数据的原有序列有关,序列越接近有序,快排效率越低。我们先观察以下图:
快排效率最好情况
快排效率最坏情况
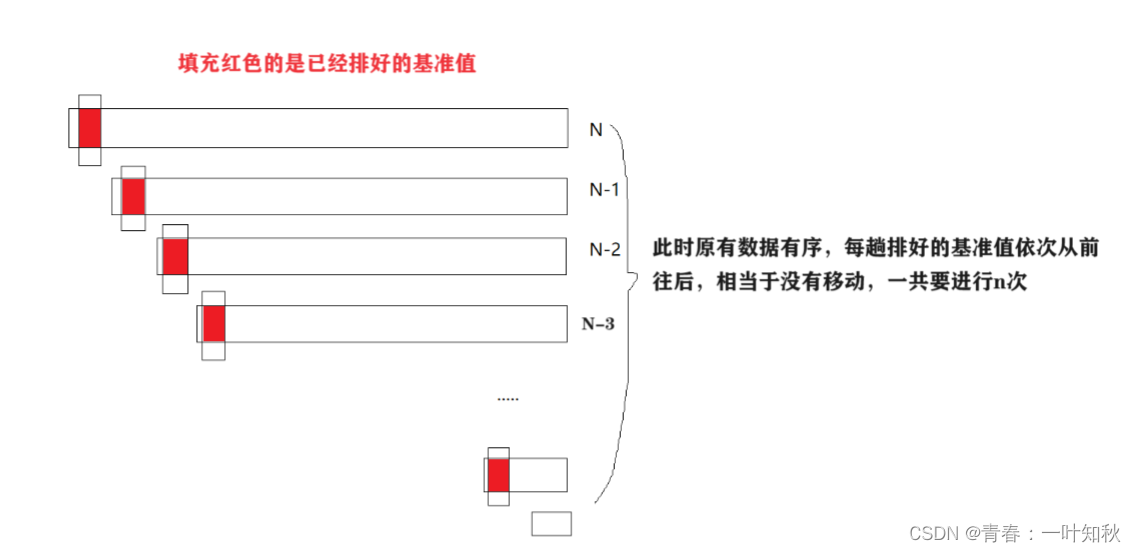
可知,快排预排序的时间效率在区间[logn,n],当原有序列越有序时,无论是递归还是非递归时间效率都很低,有序时效率最低,而遍历元素的时间复杂度不变,一直是O(n),因此快排的时间效率在区间[nlogn,n^2]。
2,三数取中
当快排在有序时(升序为例),数据会靠近左边进行排序,而要想提高快排的效率,就必须尽量让基准值尽量往中间靠拢,但这样很难控制,因为这与数据原有的序列有关。虽然说我们不能直接控制,但是我们可控制最坏情况来进而控制时间效率,即序列有序时的情况。
通常,我们是选取首元素为基准值的,因此,只要控制好首元素不为基准值的情况即可,也就是三数取中。
三数取中是将判断首元素,尾元素,中间元素三者之间的大小,将中间大的数据与首元素交换,使首元素不可能为基准值。代码如下:
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;//中间数mid
//下面比较 left mid right 三者之间大小,将中间大的数据的下标返回过去
//先人left与mid比较,然后进一步判断right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
具体思想就是先两两比较,然后进一步与第三者比较,上面代码中选举了left与mid两者之间比较,然后再跟第三者right比较,满足中间大的数据返回其下标。
3,改善后算法的运用
有了三数取中,快排将不会出现最坏情况,虽说有可能会出现次坏情况,但基本是不可能的,因为这种情况很是要求原序列的次序和三数取中的交换,因次,如若在算法中加上三数取中后算法的时间复杂度基本为O(nlogn)。下面是改进后运用的代码:
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;//中间数mid
//下面比较 left mid right 三者之间大小,将中间大的数据的下标返回过去
//先人left与mid比较,然后进一步判断right
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right]) // mid是最大值
{
return left;
}
else
{
return right;
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right]) // mid是最小
{
return left;
}
else
{
return right;
}
}
}
void Swap(int* x1, int* x2) {
int t = *x1;
*x1 = *x2;
*x2 = t;
}
//普通法
int PartSort1(int* a, int begin, int end) {
//运用三数取中,与每次预排序的区间首元素交换,防止出现最坏情况
int midi = GetMidi(a, begin, end);
Swap(a + begin, a + midi);
//以下代码正常不变
int key = begin;
while (begin < end) {
//注意此步骤,end必须先开始(即当左边开始行走右边一定有比key小的值),
//因为要控制最后的begin最终比key(开头元素)小,因此,右边必须先走.
while (begin < end && a[end] >= a[key]) {
end--;
}
//当走左边时,最终会Swap(a + end, a + begin);交换后begin的最终比key小
while (begin < end && a[begin] <= a[key]) {
begin++;
}
Swap(a + end, a + begin);
}
Swap(a + key, a + begin);
return begin;
}
//挖坑发
int PartSort2(int* a, int begin, int end) {
//运用三数取中,与每次预排序的区间首元素交换,防止出现最坏情况
int midi = GetMidi(a, begin, end);
Swap(a + begin, a + midi);
//以下代码正常不变
int key = a[begin];
int hole = begin;//开头先形成坑位
while (begin < end) {
// 右边先走(原理与PartSort1原理一样),找小,填到左边的坑,右边形成新的坑位
while (begin < end && a[end] >= key) {
end--;
}
a[hole] = a[end];
hole = end;
// 左边再走,找大,填到右边的坑,左边形成新的坑位
while (begin < end && a[begin] <= key) {
begin++;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
//前后指针法
int PartSort3(int* a, int begin, int end) {
//运用三数取中,与每次预排序的区间首元素交换,防止出现最坏情况
int midi = GetMidi(a, begin, end);
Swap(a + begin, a + midi);
//以下代码正常不变
int front = begin + 1;
int back = begin;
while (front <= end) {
if (a[front] <= a[begin]) {
back++;
Swap(a + back, a + front);
}
front++;
}
//因为后指针控制,所以当程序结束后back所指向的数据都比keyi所指向的数据小
Swap(a + begin, a + back);
return back;
}
在以上中,除了预排序算法需要改进,其它的都不用动即可实现高效的快排。最后,跟大家再次强调一下快排的效率,快排在大多数情况下确实效率很高,但快排的效率受原数据的序列影响比较大,当序列越接近有序时,快排的效率可能还没有其它算法高,在以后的运用中要不要用快排还需根据原数据的情况而定。
相关文章:

【数据结构】快排的详细讲解
目录: 介绍 一,递归快排确定基准值 二,递归遍历 三,非递归的快排 四,快排的效率 介绍 快排是排序算法中效率是比较高的,快排的基本思想是运用二分思想,与二叉树的前序遍历类似,…...
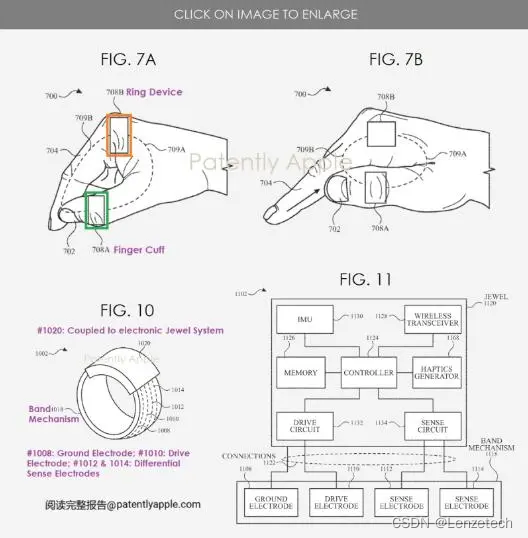
蓝牙资讯|三星推迟发布智能戒指Galaxy Ring,智能穿戴小型化是大趋势
根据外媒 The Elec 报道,Galaxy Ring这款戒指主要面向健康和 XR 头显市场,该智能戒指可能被延期至 2024 年第三季度后发布。 外媒声称三星 Galaxy Ring 的上市周期,主要取决医疗认证的相关审批时间,三星计划将在 2024 年第三季度…...

移动端tree树
注意: 这是uniapp的写法,vue想用的话需要改造一下,里边的view和text,vue不能用,改成div,span即可。 样式rpx也要改成px tree树组件(QQ群:旧群没了,新群:801142650) - …...

SpringTask ----定时任务框架 ----苍穹外卖day10
目录 SpringTask 需求分析 快速入门 使用步骤 编辑业务开发 SpringTask 定时任务场景特化的框架 需求分析 快速入门 使用cron表达式来使用该框架 使用步骤 添加注解 自定义定时任务类 重点在于以下cron表达式的书写,精确表达触发的间隔 业务开发 主task方法 time使用(-…...

Fuzz测试:发现软件隐患和漏洞的秘密武器
0x01 什么是模糊测试 模糊测试(Fuzz Testing)是一种广泛用于软件安全和质量测试的自动化测试方法。它的基本思想是向输入参数或数据中注入随机、不规则或异常的数据,以检测目标程序或系统在处理不合法、不正常或边缘情况下的行为。模糊测试通…...
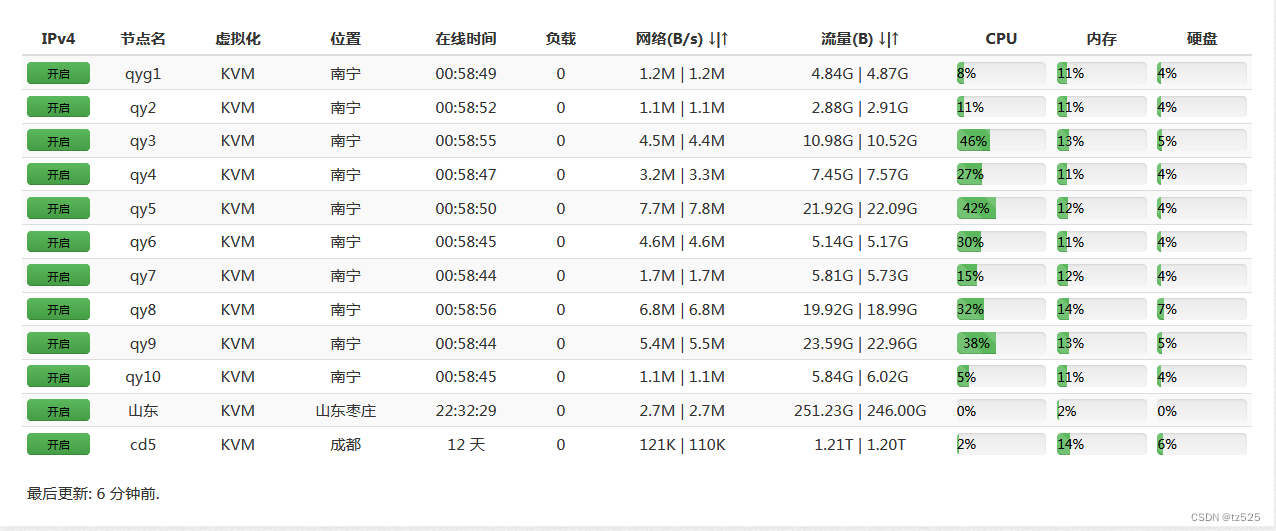
无为WiFi的一批服务器
我们在多个地区拥有高速服务器,保证网速给力,刷片无压力 嘿嘿 <?phpinclude("./includes/common.php"); $actisset($_GET[act])?daddslashes($_GET[act]):null; $urldaddslashes($_GET[url]); $authcodedaddslashes($_GET[authcode]);he…...

SpringBoot3.0——踩坑
SpringBoot3.0后有一些改动 JDK要17以上lombok <dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><version>1.18.20</version> </dependency>servlet <dependency><groupId>ja…...

Springboot的自动装配原理和文件上传FastDFS
Spring Boot的自动装配原理: Spring Boot的自动装配原理是基于约定大于配置的原则,它通过扫描类路径下的各种文件以及类的注解信息来自动配置应用程序的各种组件和功能。Spring Boot会根据约定的规则自动配置相应的Bean,这些Bean都是单例的&…...

【数据库开发】DQL操作和多表设计
数据库开发 一、数据库操作-DQL 1.概述 用来查询数据库表中的记录,查询操作分为两部分,单表操作和多表操作,针对于查询而言(相较于增删改更加的灵活)基于目标分析条件转换为SQL语句 2.语法 SELECT 字段列表 FROM表…...

用PyTorch轻松实现二分类:逻辑回归入门
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
[nltk_data] Error loading stopwords: <urlopen error [WinError 10054]
报错提示: >>> import nltk >>> nltk.download(stopwords) 按照提示执行后 [nltk_data] Error loading stopwords: <urlopen error [WinError 10054] 找到路径C:\\Users\\EDY\\nltk_data,如果没有nltk_data文件夹,在…...

基于Spring Boot的网上租贸系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

通过IP地址管理提升企业网络安全防御
在今天的数字时代,企业面临着越来越多的网络安全威胁。这些威胁可能来自各种来源,包括恶意软件、网络攻击和数据泄露。为了提高网络安全防御,企业需要采取一系列措施,其中IP地址管理是一个重要的方面 1. IP地址的基础知识 首先&a…...
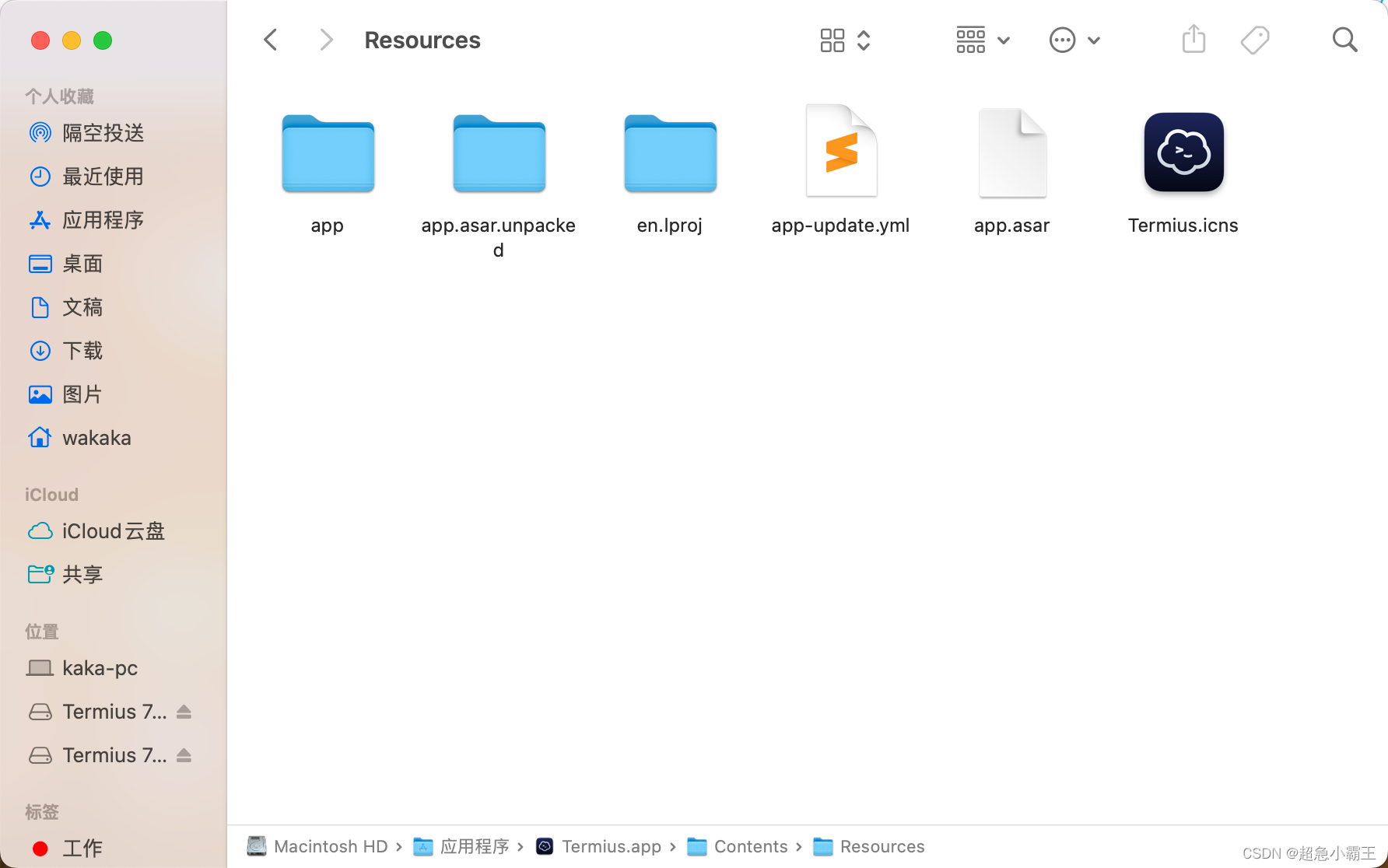
termius mac版无需登录注册直接永久使用
1. 下载地址:termius下载 2. 解压安装 3. 当出现 “termius”已损坏,无法打开 则输入以下命令即可:sudo xattr -r -d com.apple.quarantine /Applications/Termius.app 最后去 系统设置-> 隐私与安全性-> 仍要打开 4. 删除app-update.yml文件&…...

TPU编程竞赛|Stable Diffusion大模型巅峰对决,第五届全球校园人工智能算法精英赛正式启动!
目录 赛题介绍 赛题背景 赛题任务 赛程安排 评分机制 奖项设置 近日,2023第五届全球校园人工智能算法精英赛正式开启报名。作为赛题合作方,算丰承办了“算法专项赛”赛道,提供赛题「面向Stable Diffusion的图像提示语优化」,…...

微信小程序 rpx 转 px
前言 略 rpx 转 px let query wx.createSelectorQuery(); query.selectViewport().boundingClientRect(function(res){let rpx2Px 1 * (res.width/750);console.log("1rpx " rpx2Px "px"); }); query.exec();参考 https://blog.csdn.net/qq_39702…...

机器学习之旅-从Python 开始
导读你想知道如何开始机器学习吗?在这篇文章中,我将简要概括一下使用 Python 来开始机器学习的一些步骤。Python 是一门流行的开源程序设计语言,也是在人工智能及其它相关科学领域中最常用的语言之一。机器学习简称 ML,是人工智能…...
——第103天:Pyecharts绘制多种炫酷水球图参数说明+代码实战)
100天精通Python(可视化篇)——第103天:Pyecharts绘制多种炫酷水球图参数说明+代码实战
文章目录 专栏导读一、水球图介绍1. 水球图是什么?2. 水球图的应用场景二、水球图类配置选项1. 导包2. Liquid类3. add函数三、水球图实战1. 基础水球图2. 矩形水球图3. 圆棱角矩形水球图4. 三角形水球图5. 菱形水球图6. 箭头型水球图7. 修改数据精度8. 设置无边框9. 多个并排…...
好用的文件备份软件推荐!
为什么需要文件备份软件? 在我们使用计算机的日常工作生活中,可能会遇到各种不同类型的文件,例如文档、Word文档、Excel表格、PPT演示文稿、图片等,这些数据中可能有些对我们来说很重要,但是可能会因为一些意外状况…...
1130 - Host ‘192.168.10.10‘ is not allowed to connect to this MysOL server
mysql 远程登录报错误信息:1130 - Host 124.114.155.70 is not allowed to connect to this MysOL server //需要在mysql 数据库目录下修改 use mysql; //更改用户的登录主机为所有主机,%代表所有主机 update user set host% where userroot; //刷新权…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
