leetcode 221 最大正方形 + 1277 统计全为1的正方形子矩阵
题目
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
示例
输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:4
解析
题外话,首先注意下函数签名:func maximalSquare(matrix [][]byte) int {}
这道题还是用动规五部曲来处理下
1.dp数组及其含义:
dp[i][j]:代码下标为i-1,j-1位置为右下角的正方形,最大面积为dp[i][j]。这个dp公式的定义很重要,首先是定义成了右下角,其次还用到了之前-1的这种方法,写代码会简单些
2.递推公式
if matrix[i-1][j-1] == ‘1’ {
dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) + 1
}
大致的思路是,首先要右下角的这个位置是1,否则就没啥用了,肯定不满足;在是1的前提下,类似木桶原理,右下角位置的最长边长,取决于另外三个位置的最小距离,然后+1
3.初始化
使用了-1的策略后,就是不需要特别的初始化了,默认是0
func maximalSquare(matrix [][]byte) int {if len(matrix) == 0 || len(matrix[0]) == 0 {return 0}m := len(matrix)n := len(matrix[0])maxSide := 0dp := make([][]int, m+1)for i := 0; i <= m; i++ {dp[i] = make([]int, n+1)}for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if matrix[i-1][j-1] == '1' {dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) + 1maxSide = max(maxSide, dp[i][j])}}}return maxSide * maxSide
}func min(a, b int) int {if a > b {return b}return a
}func max(a, b int) int {if a > b {return a}return b
}
1277 统计全为1的正方形子矩阵
题目
给你一个 m * n 的矩阵,矩阵中的元素不是 0 就是 1,请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。
示例
输入:matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
输出:15
解释:
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.
解析
这道题和上面那道基本一样的思路,记住递推公式把
func countSquares(matrix [][]int) int {if len(matrix) == 0 || len(matrix[0]) == 0 {return 0}m := len(matrix)n := len(matrix[0])dp := make([][]int, m+1)for i := 0; i <= m; i++ {dp[i] = make([]int, n+1)}res := 0for i := 1; i <= m; i++ {for j := 1; j <= n; j++ {if matrix[i-1][j-1] == 1 {dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) + 1res += dp[i][j]}}}return res
}func min(a, b int) int {if a > b {return b}return a
}
相关文章:

leetcode 221 最大正方形 + 1277 统计全为1的正方形子矩阵
题目 在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。 示例 输入:matrix [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“…...

yolov7车牌识别(12种中文车牌类型)
12种中文车牌类型: 1.单行蓝牌 2.单行黄牌 3.新能源车牌 4.白色警用车牌 5 教练车牌 6 武警车牌 7 双层黄牌 8 双层武警 9 使馆车牌 10 港澳牌车 11 双层农用车牌 12 民航车牌 测试demo: 以yolov7-lite-s 为例: python detect_rec_plate.py --detect_model weigh…...

Mac PF命令防火墙
查看所有网络接口及其名称 ifconfig -a 文件目录:/etc/pf.conf 在文件末尾添加以下行: block drop from IP_ADDRESS其中,"IP_ADDRESS"是您要屏蔽的IP地址。 输入以下命令以重新加载pf防火墙配置文件: sudo pfctl …...
)
prototype-based learning algorithm(原型学习)
Prototype-based learning(原型学习)是一种机器学习方法,它的核心思想是通过存储一组代表性的样本(原型),然后使用这些原型来进行分类、回归或聚类等任务。这种方法模拟了人类学习的方式,人们往…...
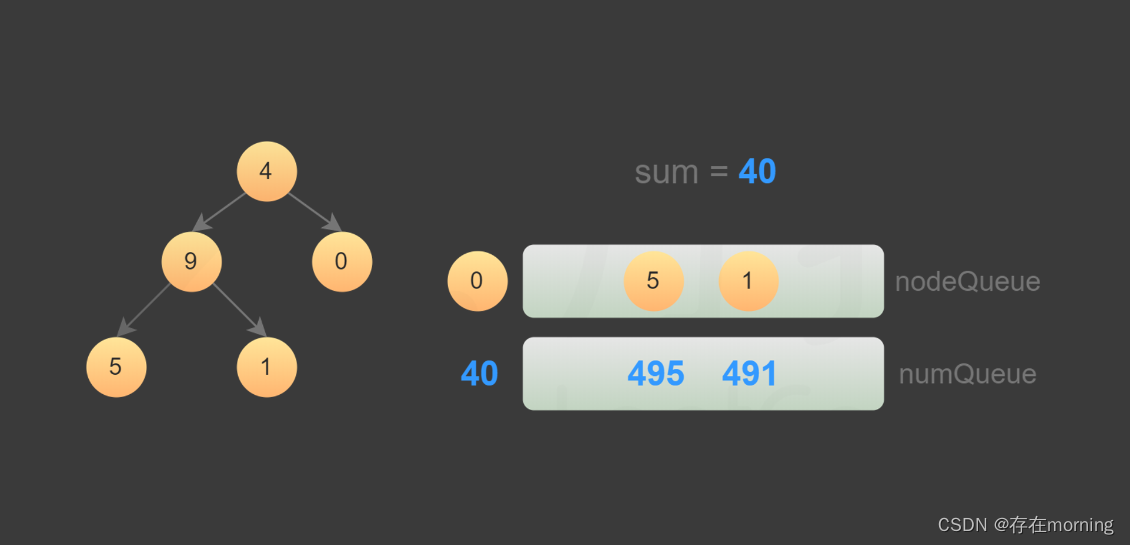
【数据结构-二叉树 八】【遍历求和】:求根到叶子节点数字之和
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【遍历求和】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&am…...

PHP知识大全
PHP知识大全 1. 变量如何定义?如何检查变量是否定义?如何删除一个变量?怎样检测变量是否设置? $定义 isset()// 检测变量是否设置 defined()// 检测常量是否设置unset()//销毁指定的变量 empty()// 检测…...

Jmeter常用参数化技巧总结!
说起接口测试,相信大家在工作中用的最多的还是Jmeter。 JMeter是一个100%的纯Java桌面应用,由Apache组织的开放源代码项目,它是功能和性能测试的工具。具有高可扩展性、支持Web(HTTP/HTTPS)、SOAP、FTP、JAVA 等多种协议。 在做…...
iTunes更新iOS17出现发生未知错误4000的原因和解决方案
有不少人使用iTunes更新iOS 17时出现「无法更新iPhone发生未知的错误4000」的错误提示,不仅不知道iTunes升级失败的原因,也无从解决iPhone无法更新4000的问题。 小编今天就分享iPhone更新iOS系统出现4000错误提示的原因和对应的解决方案。 为什么iPhone…...
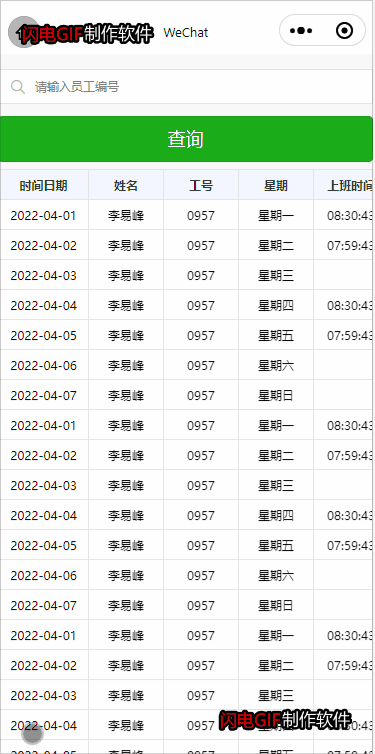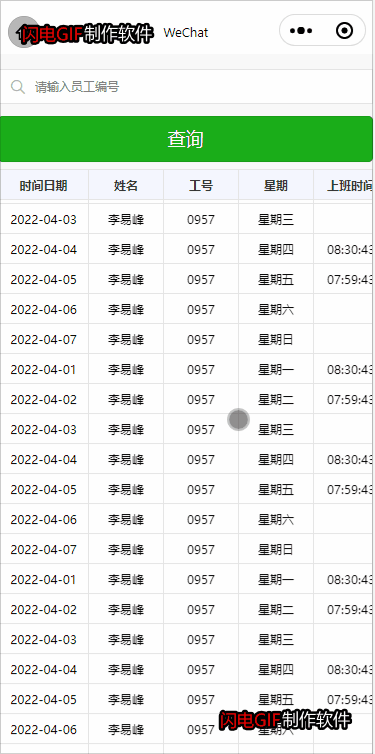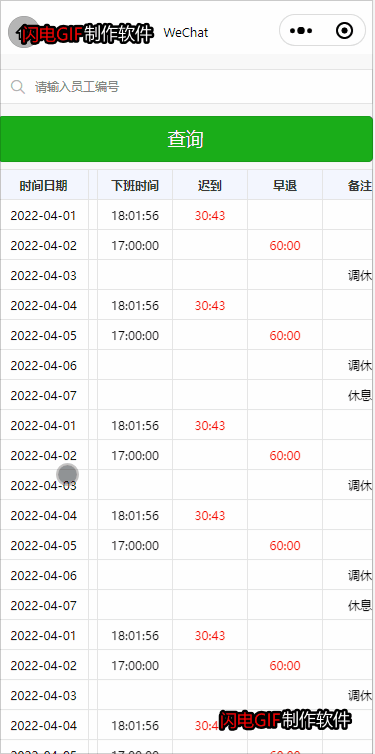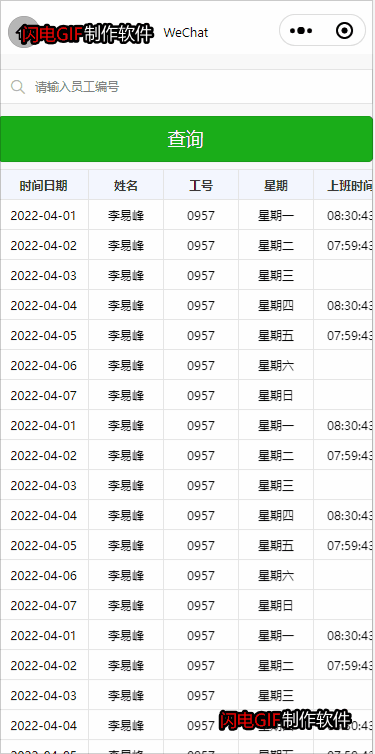
微信小程序 table表格 固定表头和首列 右侧表格可以左右滚动
(一) 1.左侧一列固定不动 2.右侧表格内容可以左右滚动 3.单元格内容平均分配 4.每一行行高可以由内容撑开 通过 js 设置左侧一列行高与右侧表格内容行高保持一致 1.1 效果图 1.2 tabble.wxml <view classtable><!-- 左侧固定 --><view classtable_left_colum…...

Final Cut Pro 10.6.10中文用法儿
Final Cut Pro是一款专业视频编辑软件,主要用于影片的后期剪辑、调色、特效、音频处理等方面。 Final Cut Pro for Mac(fcpx视频剪辑) 10.6.10中文版 以下是一些基本的使用方法和快捷键: 添加素材: 在检视器中,可以使用E快捷键把所选素材片…...

【网络安全---XSS漏洞(1)】XSS漏洞原理,产生原因,以及XSS漏洞的分类。附带案例和payload让你快速学习XSS漏洞
以pikachu靶场为例子进行讲解,pikachu靶场的搭建请参考以下博客; 【网路安全 --- pikachu靶场安装】超详细的pikachu靶场安装教程(提供靶场代码及工具)_网络安全_Aini的博客-CSDN博客【网路安全 --- pikachu靶场安装】超详细的pi…...

云计算:常用系统前端与后端框架
目录 一、理论 1.前端 2.后端 一、理论 1.前端 (1)JavaScript框架 JQuery.JS ZeptoJS(与jquery类似) SUI.Mobile Node.JS (服务端) angular.Js (模型,scope作用域,controller, 依赖注入,MVVM) :前端MVC . requir…...
asp.net闲置物品购物网系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net闲置物品购物网系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语 言开发 asp.net 闲置物品购物网 二、功…...

一般纳税人缺少进项票,如何降低税负压力?
《梅梅谈税》专注于企业税务筹划!助力企业合理、合规、合法进行节税税收筹划! 大部分一般纳税人企业通常都存在进项和成本发票欠缺的问题,而进项发票欠缺,就会导致企业的增值税和企业所得税税负压力过大,那么如何解决…...

UniAD 论文学习
一、解决了什么问题? 当前的自动驾驶方案大致由感知(检测、跟踪、建图)、预测(motion、occupancy)和规划三个模块构成。 为了实现各种功能,智驾方案大致包括两种路线。一种是针对每个任务都部署一个模型&a…...
用冒泡排序模拟实现qsort()函数交换整数)
(c语言)用冒泡排序模拟实现qsort()函数交换整数
#include<stdio.h> int cmp(const void* x1, const void* x2) { return (*(int*)x1 - *(int*)x2); } void Swap(char* x, char* y, int width) //将两个数改为char*类型,每次只交换一个字节,直到将int*的四个字节全部交换一遍 { int i 0; f…...

【Java-LangChain:使用 ChatGPT API 搭建系统-11】用 ChatGPT API 构建系统 总结篇
第十一章,用 ChatGPT API 构建系统 总结篇 本课程详细介绍了 LLM 工作原理,包括分词器(tokenizer)的细节、评估用户输入的质量和安全性的方法、使用思维链作为 Prompt、通过链式 Prompt 分割任务以及返回用户前检查输出等。 本课…...

3D 生成重建004-DreamFusion and SJC :TEXT-TO-3D USING 2D DIFFUSION
3D 生成重建004-DreamFusion and SJC :TEXT-TO-3D USING 2D DIFFUSION 文章目录 0 论文工作1 论文方法1.1论文方法1.2 CFG1.3影响1.4 SJC 2 效果 0 论文工作 对于生成任务,我们是需要有一个数据样本,让模型去学习数据分布 p ( x ) p(x) p(x…...

机械臂抓取的产业落地进展与思考
工业机械臂是一种能够模拟人类手臂动作的机械装置,具有高精度、高速度和高灵活性的特点。近年来,随着人工智能和机器人技术的快速发展,机械臂在工业生产、物流仓储、医疗护理等领域得到了广泛应用。机械臂抓取技术作为机械臂的核心功能之一&a…...
分析)
【RuoYi-Cloud项目研究】【ruoyi-auth模块】登录请求(/login)分析
文章目录 0. 网关如何处理登录请求1. Controller1.1. 获取用户信息1.2. 创建用户的token 2. Service2.1. FeignClient远程查询用户信息2.2. 验证密码 3. 何时刷新 token,如何刷新【本文重点】 本文主要是分析登录请求 /login 的过程。 调用过程是:ruoyi-…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
