sheng的学习笔记-【中文】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第二周测验
课程1_第2周_测验题
目录:目录
第一题
1.神经元计算什么?
A. 【 】神经元计算激活函数后,再计算线性函数(z=Wx+b)
B. 【 】神经元计算一个线性函数(z=Wx+b),然后接一个激活函数
C. 【 】神经元计算一个函数g,它线性地缩放输入x(Wx+b)
D. 【 】神经元先计算所有特征的平均值,然后将激活函数应用于输出
答案:
B.【 √ 】神经元计算一个线性函数(z=Wx+b),然后接一个激活函数
第二题
2.以下哪一个是逻辑回归的损失函数?
A. 【 】 L ( i ) ( y ^ ( i ) , y ( i ) ) = ∣ y ( i ) − y ^ ( i ) ∣ L^{(i)}(\hat{y}^{(i)},y^{(i)})=|y^{(i)} - \hat{y}^{(i)}| L(i)(y^(i),y(i))=∣y(i)−y^(i)∣
B. 【 】 L ( i ) ( y ^ ( i ) , y ( i ) ) = m a x ( 0 , y ( i ) − y ^ ( i ) ) L^{(i)}(\hat{y}^{(i)},y^{(i)})=max(0,y^{(i)} - \hat{y}^{(i)}) L(i)(y^(i),y(i))=max(0,y(i)−y^(i))
C. 【 】 L ( i ) ( y ^ ( i ) , y ( i ) ) = ∣ y ( i ) − y ^ ( i ) ∣ 2 L^{(i)}(\hat{y}^{(i)},y^{(i)})=|y^{(i)} - \hat{y}^{(i)}|^2 L(i)(y^(i),y(i))=∣y(i)−y^(i)∣2
D. 【 】 L ( i ) ( y ^ ( i ) , y ( i ) ) = − ( y ( i ) l o g ( y ^ ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − y ^ ( i ) ) ) L^{(i)}(\hat{y}^{(i)},y^{(i)})=-(y^{(i)}log(\hat{y}^{(i)})+(1-y^{(i)})log(1-\hat{y}^{(i)})) L(i)(y^(i),y(i))=−(y(i)log(y^(i))+(1−y(i))log(1−y^(i)))
答案:
D.【 √ 】 L ( i ) ( y ^ ( i ) , y ( i ) ) = − ( y ( i ) l o g ( y ^ ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − y ^ ( i ) ) ) L^{(i)}(\hat{y}^{(i)},y^{(i)})=-(y^{(i)}log(\hat{y}^{(i)})+(1-y^{(i)})log(1-\hat{y}^{(i)})) L(i)(y^(i),y(i))=−(y(i)log(y^(i))+(1−y(i))log(1−y^(i)))
第三题
3.假设img是一个(32, 32, 3)数组,表示一个32x32图像,它有三个颜色通道:红色、绿色和蓝色。如何将其重塑为列向量?
A. 【 】x = img.reshape((1, 32 * 32, 3))
B. 【 】x = img.reshape((32 * 32 * 3, 1))
C. 【 】x = img.reshape((3, 32 * 32))
D. 【 】x = img.reshape((32 * 32, 3))
答案:
B.【 √ 】x = img.reshape((32 * 32 * 3, 1))
第四题
4.考虑以下两个随机数组a和b:
a = np.random.randn(2, 3) # a.shape = (2, 3)
b = np.random.randn(2, 1) # b.shape = (2, 1)
c = a + b
c的维度是什么?
A. 【 】c.shape = (3, 2)
B. 【 】c.shape = (2, 1)
C. 【 】c.shape = (2, 3)
D. 【 】计算不成立因为这两个矩阵维度不匹配
答案:
C.【 √ 】c.shape = (2, 3)
第五题
5.考虑以下两个随机数组a和b:
a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a * b
c的维度是什么?
A. 【 】c.shape = (4, 3)
B. 【 】c.shape = (3, 3)
C. 【 】c.shape = (4, 2)
D. 【 】计算不成立因为这两个矩阵维度不匹配
答案:
D.【 √ 】计算不成立因为这两个矩阵维度不匹配
Note:运算符 “*” 说明了按元素乘法来相乘,但是元素乘法需要两个矩阵之间的维数相同,所以这将报错,无法计算。
第六题
6.假设每个示例有 n x n_x nx个输入特性, X = [ X ( 1 ) , X ( 2 ) … , X ( m ) ] X=[X^{(1)},X^{(2)}…,X^{(m)}] X=[X(1),X(2)…,X(m)]。 X X X的维数是多少?
A. 【 】(m, 1)
B. 【 】(1, m)
C. 【 】( n x n_x nx, m)
D. 【 】(m, n x n_x nx)
答案:
C.【 √ 】( n x n_x nx, m)
第七题
7.np.dot(a,b)对a和b的进行矩阵乘法,而a * b执行元素的乘法,考虑以下两个随机数组a和b:
a = np.random.randn(12288, 150) # a.shape = (12288, 150)
b = np.random.randn(150, 45) # b.shape = (150, 45)
c = np.dot(a, b)
c的维度是什么?
A. 【 】c.shape = (12288, 150)
B. 【 】c.shape = (150, 150)
C. 【 】c.shape = (12288, 45)
D. 【 】计算不成立因为这两个矩阵维度不匹配
答案:
C.【 √ 】c.shape = (12288, 45)
第八题
8.请考虑以下代码段:
#a.shape = (3,4)
#b.shape = (4,1)
for i in range(3): for j in range(4): c[i][j] = a[i][j] + b[j]
如何将之矢量化?
A. 【 】c = a + d
B. 【 】c = a +b.T
C. 【 】c = a.T + b.T
D. 【 】c = a.T + b
答案:
B.【 √ 】c = a +b.T
Note:a的每一行元素,逐行相加b的每一行元素
第九题
9.请考虑以下代码段:
a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a * b
c的维度是什么?
A. 【 】这会触发广播机制,b会被复制3次变成(3, 3),而 * 操作是元素乘法,所以c.shape = (3, 3)
B. 【 】这会触发广播机制,b会被复制3次变成(3, 3),而 * 操作是矩阵乘法,所以c.shape = (3, 3)
C. 【 】这个操作将一个3x3矩阵乘以一个3x1的向量,所以c.shape = (3, 1)
D. 【 】这个操作会报错,因为你不能用 * 对这两个矩阵进行操作,你应该用np.dot(a, b)
答案:
A.【 √ 】这会触发广播机制,b会被复制3次变成(3,3),而 * 操作是元素乘法,所以c.shape = (3, 3)
第十题
10.请考虑以下计算图:

输出J是?
A. 【 】J = (c - 1) * (b + a)
B. 【 】J = (a - 1) * (b + c)
C. 【 】J = a * b + b * c + a * c
D. 【 】J = (b - 1) * (c + a)
答案:
B.【 √ 】J = (a - 1) * (b + c)
相关文章:

sheng的学习笔记-【中文】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第二周测验
课程1_第2周_测验题 目录:目录 第一题 1.神经元计算什么? A. 【 】神经元计算激活函数后,再计算线性函数(zWxb) B. 【 】神经元计算一个线性函数(zWxb),然后接一个激活函数…...

前端代码格式化规范总结
在日常开发过程中,经常会碰到代码格式化不一致的问题,还要就是 js 代码语法错误等没有及时发行改正,下面就介绍一下如何使用eslint、prettier、husky、lint-staged、commitizen来规范代码格式和提高代码质量的方法。 目录 准备工作代码检测代…...

Windows10打开应用总是会弹出提示窗口的解决方法
用户们在Windows10电脑中打开应用程序,遇到了总是会弹出提示窗口的烦人问题。这样的情况会干扰到用户的正常操作,给用户带来不好的操作体验,接下来小编给大家详细介绍关闭这个提示窗口的方法,让大家可以在Windows10电脑中舒心操作…...

易点易动固定资产管理系统: 帮助您应对2023年年终固定资产大盘点
作为一名企业的行政人员,我们都了解年终固定资产盘点对于企业来说至关重要。然而,面对众多资产、复杂的流程和繁琐的记录工作,往往会令人感到头疼不已。为了帮助您应对2023年的年终固定资产大盘点,我们推荐易点易动固定资产管理系…...

OpenGLES:绘制一个混色旋转的3D立方体
效果展示 混色旋转的3D立方体 一.概述 之前关于OpenGLES实战开发的博文,不论是实现相机滤镜还是绘制图形,都是在2D纬度 这篇博文开始,将会使用OpenGLES进入3D世界 本篇博文会实现一个颜色渐变、旋转的3D立方体 动态3D图形的绘制…...
Maven(4)-利用intellij idea创建maven 多模块项目
本文通过一个例子来介绍利用maven来构建一个多模块的jave项目。开发工具:intellij idea。 一、项目结构 multi-module-project是主工程,里面包含两个模块(Module): web-app是应用层,用于界面展示ÿ…...
8年测试老鸟,性能测试-数据库连接池问题定位/分析,一篇打通...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、环境准备 1&a…...
【Sentinel】Sentinel原码分析
本文内容来自【黑马】Sentinel从使用到源码解读笔记,做了部分修改和补充 目录 Sentinel 基本概念 基本流程 Node Entry 定义资源的两种方式 使用try-catch定义资源 使用注解标记资源 基于注解标记资源的实现原理 Context 什么是Context Context的初始化 …...

计算机竞赛 题目:基于深度学习的人脸表情识别 - 卷积神经网络 竞赛项目 代码
文章目录 0 简介1 项目说明2 数据集介绍:3 思路分析及代码实现3.1 数据可视化3.2 数据分离3.3 数据可视化3.4 在pytorch下创建数据集3.4.1 创建data-label对照表3.4.2 重写Dataset类3.4.3 数据集的使用 4 网络模型搭建4.1 训练模型4.2 模型的保存与加载 5 相关源码6…...
)
基于aarch64分析kernel源码 五:idle进程(0号进程)
一、参考 linux — 0号进程,1号进程,2号进程 - 流水灯 - 博客园 (cnblogs.com) Linux0号进程,1号进程,2号进程_0号进程和1号进程-CSDN博客 二、idle进程的创建流程 start_kernel --> arch_call_rest_init --> rest_init…...
【Linux】 vi / vim 使用
天天用vim 或者vi 。看着大佬用的很6 。我们却用的很少。今天咱们一起系统学习一下。 vi / vim 发展史 vi 是一款由加州大学伯克利分校,Bill Joy研究开发的文本编辑器。 vim Vim是一个类似于Vi的高度可定制的文本编辑器,在Vi的基础上改进和增加了很多…...
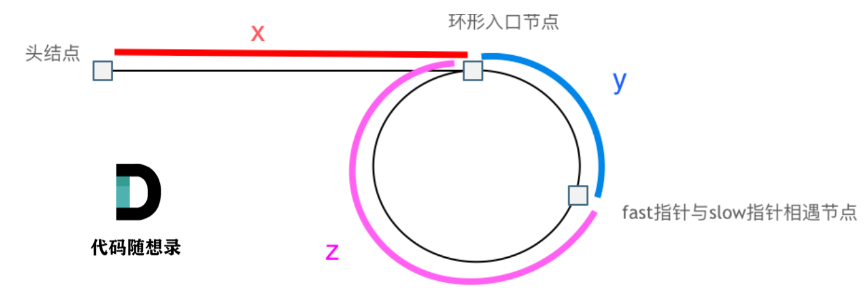
Leetcode hot 100之双指针(快慢指针、滑动窗口)
目录 数组 有序的平方仍有序 删除/覆盖元素 移动零:交换slow和fast 滑动窗口:最短的连续子串(r可行解->l--最短解) 最小长度的子数组 求和:sort、l i 1, r len - 1 三数之和abctarget 四数之和abcdtarg…...

Bridge Champ助力我国桥牌阔步亚运, Web3游戏为传统项目注入创新活力
本届杭州亚运会,中国桥牌队表现杰出,共斩获1金1银1铜佳绩,其中女子团体夺得冠军,混合团体获得亚军。这充分展现了我国桥牌的实力,也彰显了桥牌作为亚运会体育竞技项目的影响力。与此同时,Web3游戏Bridge Champ为传统桥牌项目带来创新模式,将有望推动桥牌运动在亚运舞台上焕发新…...
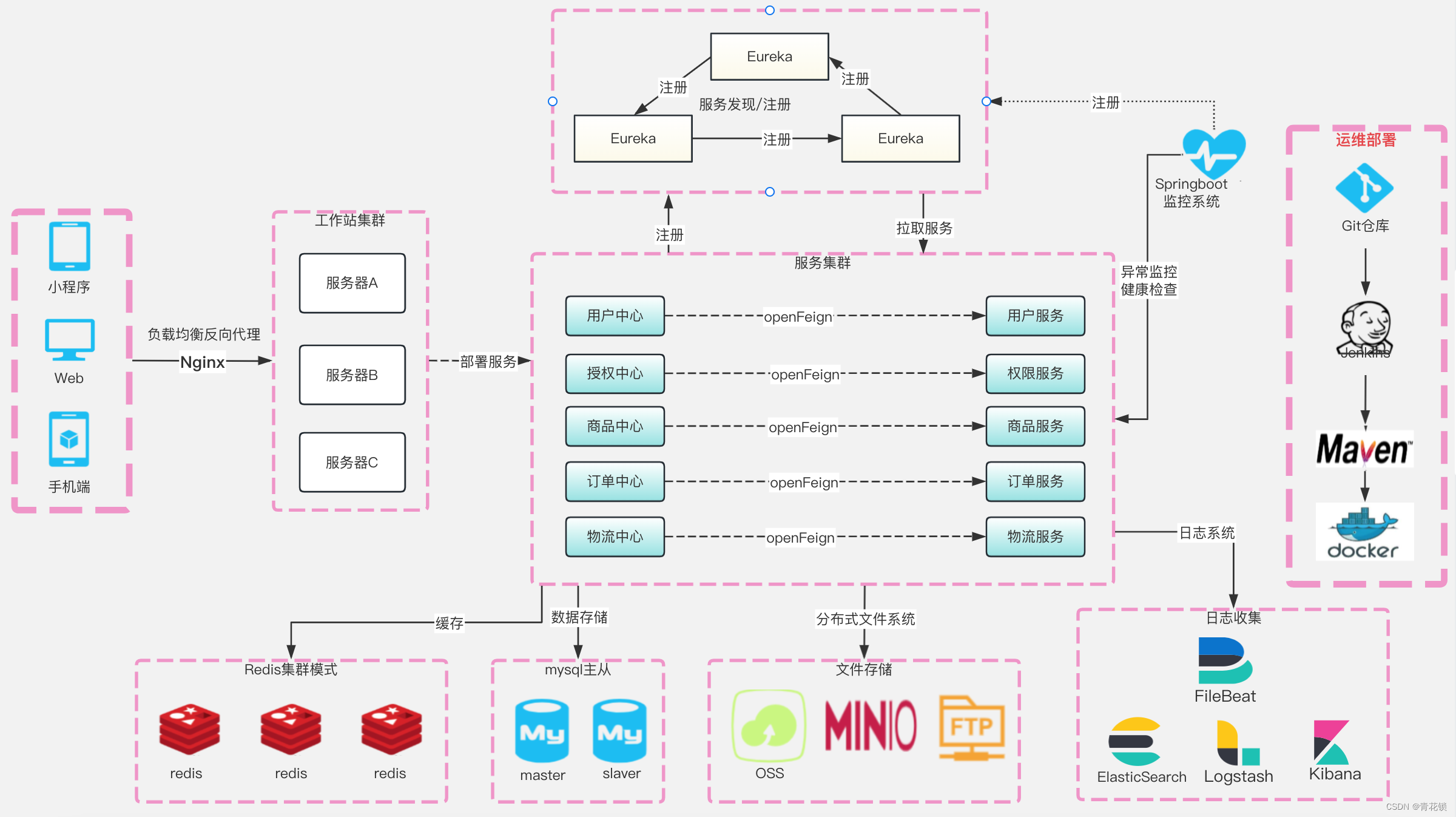
云原生微服务 第六章 Spring Cloud中使用OpenFeign
系列文章目录 第一章 Java线程池技术应用 第二章 CountDownLatch和Semaphone的应用 第三章 Spring Cloud 简介 第四章 Spring Cloud Netflix 之 Eureka 第五章 Spring Cloud Netflix 之 Ribbon 第六章 Spring Cloud 之 OpenFeign 文章目录 系列文章目录前言1、OpenFeign的实现…...
)
uniapp-vue3 抖音小程序开发(上线项目开源)
最近公司临时接一个项目来接手别人的流量,项目比较小,时间比较赶。 需求:一个答题小程序,通过答题来实现性格测算和分析。 之前开发过支付宝小程序和微信小程序,这次是首次开发抖音小程序,老板要求只能下…...

基于微信小程序的个人健康数据管理平台设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...
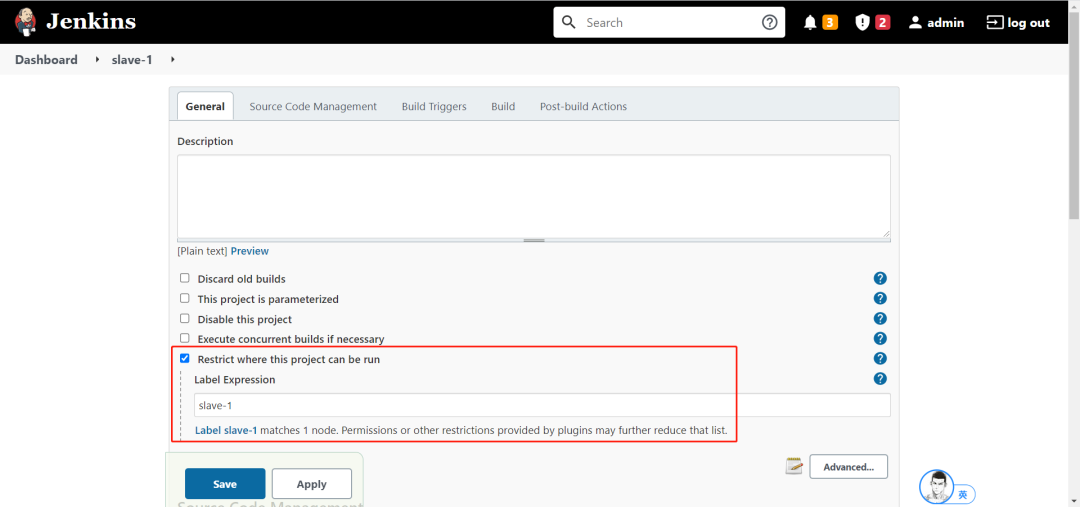
真香!Jenkins 主从模式解决问题So Easy~
01.Jenkins 能干什么 Jenkins 是一个开源软件项目,是基于 Java 开发的一种持续集成工具,用于监控持续重复的工作,旨在提供一个开放易用的软件平台,使软件项目可以进行持续集成。 中文官网:https://jenkins.io/zh/ 0…...
Win10系统打开组策略编辑器的两种方法
组策略编辑器是Win10电脑中很实用的工具,它可以帮助用户管理和设置计算机的安全性、网络连接、软件安装等各种策略。但是,很多新手用户不知道打开Win10电脑中组策略编辑器的方法步骤,下面小编给大家介绍两种简单的方法,帮助打开快…...

git 的行结束符
CR (Carriage Return) 表示<回车>LF (Line Feed) 表示<换行> 1. 不同系统的行结束符 系统名称行结束符意义释义git line endings选项DOS / Windows\r\nCRLF‘\r’是使光标移动到行首 ’\n’是使光标下移一行Windows-styleMacOS\rCRreturnAs-isUNIX / Linux\nLFne…...
buuctf PWN warmup_csaw_2016
下载附件,IDA查看 发现直接有显示flag函数 int sub_40060D() {return system("cat flag.txt"); }查看程序起始地址0x40060D ; Attributes: bp-based framesub_40060D proc near ; __unwind { push rbp mov rbp, rsp mov edi, offset comman…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
