当前位置： 首页 > news >正文

Dijkstra 邻接表表示算法 | 贪心算法实现--附C++/JAVA实现源码

news 2026/2/9 1:38:48

以下是详细步骤。 

  1. 创建大小为 V 的最小堆，其中 V 是给定图中的顶点数。最小堆的每个节点包含顶点编号和顶点的距离值。 
  2. 以源顶点为根初始化最小堆（分配给源顶点的距离值为0）。分配给所有其他顶点的距离值为 INF（无限）。 
  3. 当最小堆不为空时，执行以下操作：
    1. 从最小堆中提取具有最小距离值节点的顶点。令提取的顶点为u。 
    2. 对于 u 的每个相邻顶点 v，检查 v 是否在最小堆中。如果v在Min Heap中并且距离值大于uv的权重加上u的距离值，则更新v的距离值。

让我们通过下面的例子来理解。令给定的源顶点为 0 

 

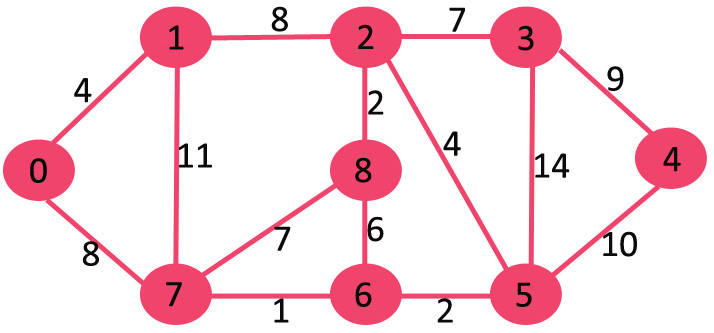
8dc4df6d86d36d8246549dc9f7b13def.jpeg

最初，源顶点的距离值为 0，所有其他顶点的距离值为 INF（无穷大）。因此，从最小堆中提取源顶点，并更新与 0（1 和

相关文章：

Dijkstra 邻接表表示算法 | 贪心算法实现--附C++/JAVA实现源码

以下是详细步骤。 创建大小为 V 的最小堆，其中 V 是给定图中的顶点数。最小堆的每个节点包含顶点编号和顶点的距离值。 以源顶点为根初始化最小堆（分配给源顶点的距离值为0）。分配给所有其他顶点的距离值为 INF（无限）。 当最小堆不为空时，执行以下操作： 从最小堆中提取…...

编程日记 2023/10/10 5:28:09

从城市吉祥物进化到虚拟人IP需要哪些步骤？

在2023年成都全国科普日主场活动中，推出了全国首个科普数字形象大使“科普熊猫”，科普熊猫作为成都科普吉祥物，是如何进化为虚拟人IP，通过动作捕捉、AR等技术，活灵活现地出现在大众眼前的？ 以广州虚拟动力虚…...

编程日记 2023/10/10 5:27:08

认识SQLServer

深入认识SQL Server：从基础到高级的数据库管理 在当今数字时代，数据是企业成功的关键。为了存储、管理和分析数据，数据库管理系统（DBMS）变得至关重要。其中，Microsoft SQL Server是一款备受欢迎的关系型数据…...

编程日记 2023/10/10 5:25:06

Python开发IDE的比较：PyCharm vs. VS Code vs. Jupyter

Python开发IDE的比较：PyCharm vs. VS Code vs. Jupyter Python开发社区中已经存在了相当长时间的持续争论：PyCharm vs. VS Code vs. Jupyter。 PyCharm：专业人士的选择 让我们从PyCharm开始。它是一个功能强大的集成开发环境（I…...

编程日记 2023/10/10 5:24:04

1206. 设计跳表

不使用任何库函数&#xff0c;设计一个 跳表 。 class Skiplist {int level0;Node headnull;public Skiplist() {}public boolean search(int target) {Node curhead;while(cur!null){while(cur.right!null&&cur.right.val<target){curcur.right;}if(cur.right!nul…...

编程日记 2023/10/10 5:22:02

【API要返回一棵树的结构】数据库表结构是平铺的数据，但是api要实现树状结构展示。api实现一棵树的结构，如何实现呢，递归？如何递归呢

数据库中的数据是平铺的&#xff0c;一行行的&#xff0c;但是api要查询出来的数据要求是一棵树的结构&#xff0c; 怎么把平铺的数据转换成树状结构呢&#xff1f; public List<CarbonRepo> findCarbonRepo(Integer type){// 1. 先查出所有数据。 baseFindList 方法就是…...

编程日记 2023/10/10 5:21:01

视频批量剪辑工具，自定义视频速率，批量剪辑工具助力创意无限”

在视频制作的世界里&#xff0c;每一个细节都至关重要。今天&#xff0c;让我们来探索一项强大且创新的功能——自定义视频速率。利用它&#xff0c;你可以轻松地调整视频播放速度&#xff0c;赋予你的作品独特的个性和风格。 首先第一步&#xff0c;我们要打开好简单批量智剪…...

编程日记 2023/10/10 5:19:59

starrocks启动和停止和重启脚本

StarRocks启动和停止和重启脚本 编辑脚本&#xff1a;vim start_stop_starrocks.sh 备注:IP修改为自己的IP即可 #!/bin/bashcase $1 in "start"){for i in 12.3.7.147 12.3.7.148 12.3.7.149 12.3.7.150doecho " --------启动 $i be -------"ssh $i &qu…...

编程日记 2023/10/10 5:18:58

升级Xcode 15后，出现大量Duplicate symbols问题

https://developer.apple.com/forums/thread/731090 升级到Xcode 15后&#xff0c;原先Xcode14可以编译的项目出现大量Duplicate symbols&#xff0c;且引用报错指向同一个路径&#xff08;一般为Framework&#xff09;下的同一个文件。经过查找相关解决&#xff0c;可通过添加…...

编程日记 2023/10/10 5:17:56

Godot2D角色导航教程（角色随鼠标移动）

文章目录 运行结果2D导航概述开始前的准备2D导航创建导航网格创建角色 其他文章 运行结果 2D导航概述 Godot为2D和3D游戏提供了多个对象、类和服务器&#xff0c;以便于基于网格或基于网格的导航和路径查找。 说到导航&#xff0c;就得说一下导航网格&#xff0c;导航网格定义…...

编程日记 2023/10/10 5:16:55

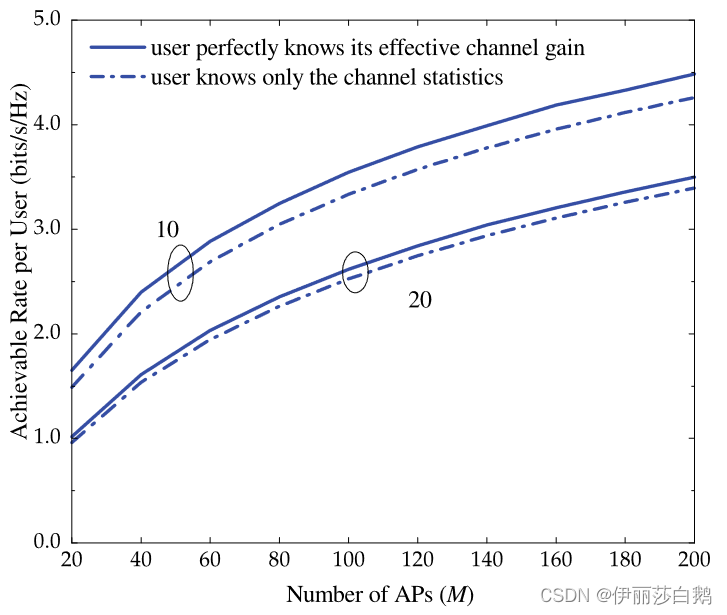
论文阅读--Cell-free massive MIMO versus small cells

无蜂窝大规模MIMO与小蜂窝网络 论文信息 Ngo H Q, Ashikhmin A, Yang H, et al. Cell-free massive MIMO versus small cells[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1834-1850. 无蜂窝大规模MIMO中没有小区或者小区边界的界定&#xff0c;所有接入…...

编程日记 2023/10/10 5:15:54

【深度学习】UniControl 一个统一的扩散模型用于可控的野外视觉生成

论文&#xff1a;https://arxiv.org/abs/2305.11147 代码&#xff1a;https://github.com/salesforce/UniControl#data-preparation docker快速部署&#xff1a;https://qq742971636.blog.csdn.net/article/details/133129146 文章目录 AbstractIntroductionRelated WorksUniCo…...

编程日记 2023/10/10 5:14:52

使用ChatGPT和MindShow一分钟生成PPT模板

对于最近学校组织的实习答辩&#xff0c;由于时间太短了&#xff0c;而且小编也特别的忙&#xff0c;于是就用ChatGPT结合MindShow一分钟快速生成PPT&#xff0c;确实很实用。只要你跟着小编后面&#xff0c;你也可以快速制作出这个PPT&#xff0c;下面小编就来详细介绍一下&am…...

编程日记 2023/10/10 5:13:51

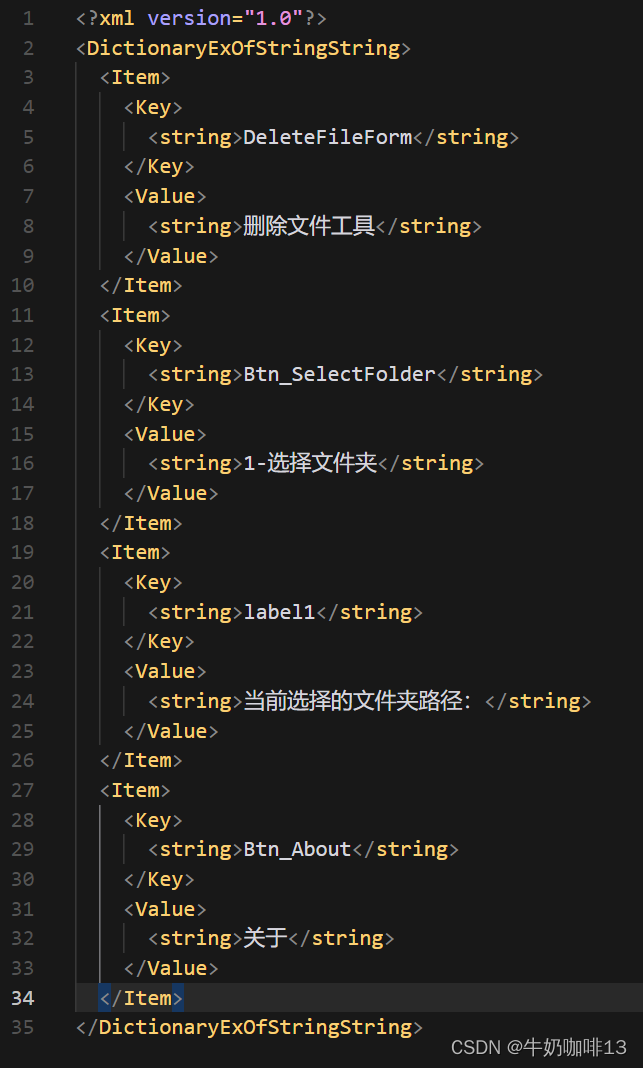
C#对字典容器Dictionary＜TKey, TValue＞内容进行XML序列化或反序列化报错解决方法

一、问题描述 在使用C#对字典容器Dictionary<TKey, TValue>内容进行XML序列化报错【System.Exception:“不支持类型 System.Collections.Generic.Dictionary2[[System.String, mscorlib, Version2.0.0.0, Cultureneutral, PublicKeyTokenb77a5c561934e089],[System.Strin…...

编程日记 2023/10/10 5:12:50

【Linux】Linux 之用户管理

Linux 之用户管理 1.Linux 下的用户2.配置文件3.用户管理3.1 useradd3.1.1 创建用户并指定用户 ID3.1.2 指定用户的主目录3.1.3 指定用户的主组 3.2 adduser3.3 userdel3.4 密码文件3.4.1 字段含义解释3.4.2 给用户添加密码 3.5 其他与用户相关的命令 4.修改用户的信息4.1 user…...

编程日记 2023/10/10 5:11:49

NLP：Attention和self-attention的区别

核心思想是根据不同的上下文为不同的信息分配不同的注意力权重 效果&#xff1a; Attention&#xff1a;它允许模型在解码时聚焦于输入的特定部分&#xff0c;从而更好地捕获上下文信息。Self-attention&#xff1a;它帮助模型捕获输入序列内部的关系&#xff0c;无论这些关系…...

编程日记 2023/10/10 5:10:48

Gap Year Plan

Gap Year Plan gap year 几个大方向 健康 60 KG10 新朋友 钱 5W RMB基本常识、社会机制补齐开网店 英语 TOELF日常交流 & 面试 口语Science Research Writing 2nd 课程 科研常识CMU 15-445MIT 6.824CMU 15-721Full Stack OpenDDIA 实习 GSOC 2024 PostgreSQL / …...

编程日记 2023/10/10 5:09:47

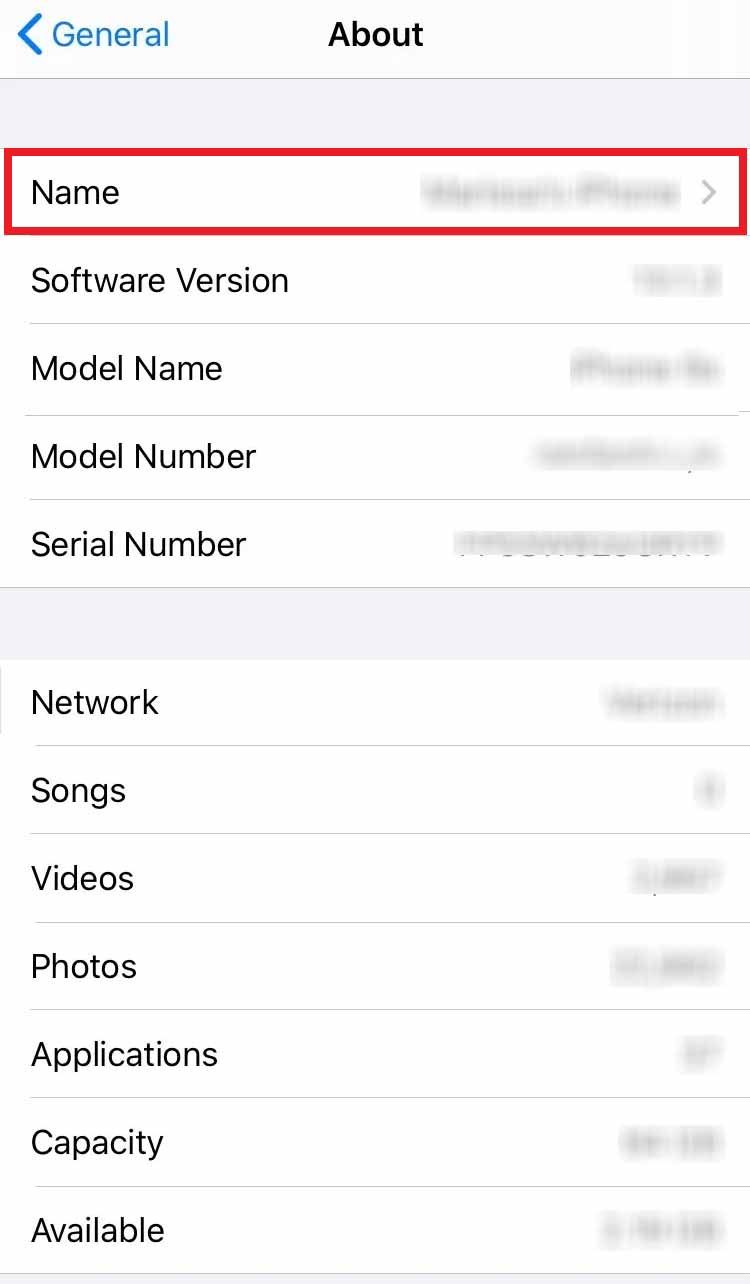
厌烦了iPhone默认的热点名称？如何更改iPhone上的热点名称

你对你默认的热点名称感到厌倦了吗&#xff1f;这篇文章是为你准备的。在这里&#xff0c;你可以了解如何轻松更改iPhone上的热点名称。 个人热点会将你的手机数据转换为Wi-Fi信号。手机上的个人热点使用户能够与其他用户共享其蜂窝数据连接。当你在WIFI网络之外时&#xff0c…...

编程日记 2023/10/10 5:08:46

【数据库审计】2023年数据库审计厂家汇总

我们大家都知道数据库审计的重要意义&#xff0c;不仅可以满足等保合规&#xff0c;还能进行风险告警&#xff0c;保障数据安全。那你知道目前市面上数据库审计厂家有哪些吗&#xff1f;这里小编就给大家汇总一下。 2023年数据库审计厂家汇总 1、行云管家 2、安恒信息 3、…...

编程日记 2023/10/10 5:07:45

C#WPF StackPanel布局及Border边框应用实例

本文介绍C#WPF StackPanel布局及Border边框应用实例，通过演示掌握StackPanel布局及Border边框用法，并对对齐方式、边距、尺寸设置、Border的圆角使用作了演示。 具体概念本文不再赘述。 Xaml文件： <Windowx:Class="PropertyDemo.MainWindow"xmlns="htt…...

编程日记 2023/10/10 5:06:44

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造&#xff0c;完美适配AGV和无人叉车。同时&#xff0c;集成以太网与语音合成技术&#xff0c;为各类高级系统&#xff08;如MES、调度系统、库位管理、立库等&#xff09;提供高效便捷的语音交互体验。 L…...

编程新知 2026/2/8 4:23:14

大话软工笔记—需求分析概述

需求分析&#xff0c;就是要对需求调研收集到的资料信息逐个地进行拆分、研究&#xff0c;从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要&#xff0c;后续设计的依据主要来自于需求分析的成果&#xff0c;包括: 项目的目的…...

编程新知 2026/1/28 10:58:50

Appium+python自动化（十六）- ADB命令

简介 Android 调试桥(adb)是多种用途的工具&#xff0c;该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具&#xff0c;其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利&#xff0c;如安装和调试…...

编程新知 2026/1/21 18:20:51

黑马Mybatis

Mybatis 表现层&#xff1a;页面展示 业务层&#xff1a;逻辑处理 持久层&#xff1a;持久数据化保存 在这里插入图片描述 Mybatis快速入门 ![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/6501c2109c4442118ceb6014725e48e4.png //logback.xml <?xml ver…...

编程新知 2026/1/22 14:22:27

R语言AI模型部署方案：精准离线运行详解

R语言AI模型部署方案：精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案，实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点： 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

编程新知 2025/12/6 1:56:35

Qwen3-Embedding-0.6B深度解析：多语言语义检索的轻量级利器

第一章 引言&#xff1a;语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域&#xff0c;文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量&#xff0c;支撑着搜索引擎、推荐系统、…...

编程新知 2025/11/6 8:47:31

【单片机期末】单片机系统设计

主要内容&#xff1a;系统状态机&#xff0c;系统时基&#xff0c;系统需求分析&#xff0c;系统构建&#xff0c;系统状态流图 一、题目要求 二、绘制系统状态流图 题目&#xff1a;根据上述描述绘制系统状态流图&#xff0c;注明状态转移条件及方向。 三、利用定时器产生时…...

编程新知 2026/1/31 12:27:36

CMake控制VS2022项目文件分组

我们可以通过 CMake 控制源文件的组织结构，使它们在 VS 解决方案资源管理器中以“组”（Filter）的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总（共4种） 方法描述是否推荐…...

编程新知 2025/12/4 15:47:17

uniapp手机号一键登录保姆级教程（包含前端和后端）

目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号&#xff08;第三种&#xff09;后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

编程新知 2026/1/27 2:03:36

软件工程 期末复习

瀑布模型&#xff1a;计划 螺旋模型&#xff1a;风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合&#xff1a;模块内部功能紧密 模块之间依赖程度小 高内聚&#xff1a;指的是一个模块内部的功能应该紧密相关。换句话说&#xff0c;一个模块应当只实现单一的功能…...

编程新知 2026/2/7 0:13:47