Fourier变换中的能量积分及其详细证明过程
Fourier变换中的能量积分及其详细证明过程
在使用Fourier变换分析信号时候,有时需要用到能量积分。本文对Fourier变换的能量积分进行分析。
一、Fourier变换中的能量积分
若 F ( ω ) = F [ f ( t ) ] F(\omega)=\mathscr F[f(t)] F(ω)=F[f(t)],则有
∫ − ∞ + ∞ [ f ( t ) ] 2 d t = 1 2 π ∫ − ∞ + ∞ ∣ F ( ω ) ∣ 2 d ω (1) \int_{ - \infty }^{ + \infty } [{f}(t)]^2 {\rm{d}}t = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty }| {F}(\omega )|^2 {\rm{d}}\omega \tag1 ∫−∞+∞[f(t)]2dt=2π1∫−∞+∞∣F(ω)∣2dω(1)
该等式又称为Parseval等式。
二、证明Fourier变换中的能量积分(Parseval 等式)
证明:
根据Fourier变换的乘积定理的推论,令 f 1 ( t ) = f 2 ( t ) = f ( t ) f_1(t)=f_2(t)=f(t) f1(t)=f2(t)=f(t),则
∫ − ∞ + ∞ [ f ( t ) ] 2 d t = ∫ − ∞ + ∞ f ( t ) f ( t ) d t = 1 2 π ∫ − ∞ + ∞ F ( ω ) ‾ F ( ω ) d ω = 1 2 π ∫ − ∞ + ∞ ∣ F ( ω ) ∣ 2 d ω = 1 2 π ∫ − ∞ + ∞ S ( ω ) d ω \int_{ - \infty }^{ + \infty } [{f}(t)]^2 {\rm{d}}t = \int_{ - \infty }^{ + \infty } {{{f}(t)} } {f}(t){\rm{d}}t \\\\= \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {\overline {{F}(\omega )} } {F}(\omega ){\rm{d}}\omega\\\\= \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty }| {F}(\omega )|^2 {\rm{d}}\omega\\\\= \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {S}(\omega ) {\rm{d}}\omega ∫−∞+∞[f(t)]2dt=∫−∞+∞f(t)f(t)dt=2π1∫−∞+∞F(ω)F(ω)dω=2π1∫−∞+∞∣F(ω)∣2dω=2π1∫−∞+∞S(ω)dω
其中, S ( ω ) = ∣ F ( ω ) ∣ 2 {S}(\omega )=|{F}(\omega )|^2 S(ω)=∣F(ω)∣2,并将 S ( ω ) {S}(\omega ) S(ω)称为能量密度函数(或称为能量谱密度)。
证毕.
注解:关于Fourier变换的乘积定理及其推论和证明过程(见本博主文章:链接: Fourier变换的乘积定理及其详细证明过程).
能量密度函数 S ( ω ) {S}(\omega ) S(ω)决定了函数 f ( t ) f(t) f(t)的能量在频域的分布规律,将 S ( ω ) {S}(\omega ) S(ω)对所有频率积分就得到 f ( t ) f(t) f(t)在时间域 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞)范围的总能量 ∫ − ∞ + ∞ [ f ( t ) ] 2 d t \int_{ - \infty }^{ + \infty } [{f}(t)]^2 {\rm{d}}t ∫−∞+∞[f(t)]2dt。因此,Parseval等式又称为能量积分。
此外,还可知能量密度函数 S ( ω ) {S}(\omega ) S(ω)是一个偶函数,即
S ( ω ) = S ( − ω ) {S}(\omega )={S}(-\omega ) S(ω)=S(−ω).
三、能量积分(Parseval等式)特别注意事项
- 在 ∫ − ∞ + ∞ [ f ( t ) ] 2 d t = 1 2 π ∫ − ∞ + ∞ ∣ F ( ω ) ∣ 2 d ω \int_{ - \infty }^{ + \infty } [{f}(t)]^2 {\rm{d}}t = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty }| {F}(\omega )|^2 {\rm{d}}\omega ∫−∞+∞[f(t)]2dt=2π1∫−∞+∞∣F(ω)∣2dω等式中, ∣ F ( ω ) ∣ 2 |{F}(\omega )|^2 ∣F(ω)∣2表示对 F ( ω ) F(\omega) F(ω)取模后再平方,而不能写成 [ F ( ω ) ] 2 [{F}(\omega )]^2 [F(ω)]2,此处要特别留意该差别。
- 能量密度函数 S ( ω ) {S}(\omega ) S(ω)是一个偶函数,即 S ( ω ) = S ( − ω ) {S}(\omega )={S}(-\omega ) S(ω)=S(−ω),它不等于 f ( t ) f(t) f(t)的傅里叶变换(即能量谱密度和频谱是两种不同的计算过程);而是能量密度函数 S ( ω ) {S}(\omega ) S(ω)等于 f ( t ) f(t) f(t)的傅里叶变换后取模再平方而得到。
相关文章:

Fourier变换中的能量积分及其详细证明过程
Fourier变换中的能量积分及其详细证明过程 在使用Fourier变换分析信号时候,有时需要用到能量积分。本文对Fourier变换的能量积分进行分析。 一、Fourier变换中的能量积分 若 F ( ω ) F [ f ( t ) ] F(\omega)\mathscr F[f(t)] F(ω)F[f(t)],则有 ∫…...

保护 Web 服务器安全性
面向公众的系统(如 Web 服务器)经常成为攻击者的目标,如果这些业务关键资源没有得到适当的保护,可能会导致安全攻击,从而导致巨大的财务后果,并在客户中失去良好的声誉。 什么是网络服务器审核 当有人想要…...

docker数据管理和网络通信
docker数据管理 管理 Docker 容器中数据主要有两种方式: 数据卷(Data Volumes)和数据卷容器(DataVolumes Containers)。 1.数据卷 数据卷是一个供容器使用的特殊目录,位于容器中。可将宿主机…...

代理IP与Socks5代理:网络工程师的神奇魔法棒
网络工程师是数字世界的魔法师,而代理IP和Socks5代理则是他们的神奇魔法棒。这两项技术在跨界电商、爬虫、出海业务、网络安全和游戏等领域中,为网络工程师提供了强大的工具,让他们能够创造技术的奇迹。本文将深入研究这些神奇魔法棒在不同领…...

【K8S系列】深入解析k8s 网络插件—kube-router
序言 做一件事并不难,难的是在于坚持。坚持一下也不难,难的是坚持到底。 文章标记颜色说明: 黄色:重要标题红色:用来标记结论绿色:用来标记论点蓝色:用来标记论点 在现代容器化应用程序的世界中…...

Flutter的Platform介绍-跨平台开发,如何根据不同平台创建不同UI和行为
文章目录 Flutter跨平台概念介绍跨平台开发平台相关性Platform ChannelPlatform-specific UIPlatform Widgets 如何判断当前是什么平台实例 Platform 类介绍获取当前平台的名称检查当前平台其他属性 利用flutter设计跨Android和IOS平台应用的技巧1. 遵循平台的设计准则2. 使用平…...

gitlab docker部署,备份,恢复
本次安装在CentOS7下进行 1、安装yum 检查是否已经安装yum yum --version如果未安装 sudo yum install -y yum-utils添加镜像源: 国外镜像源:yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo阿里镜像源&am…...

腾讯云/阿里云国际站代理:阿里云、华为云和腾讯云“大展拳脚”,与国际巨头未来竞争焦点是AI计算?
国内云计算市场重新掀起的价格战,腾讯云国际站代理让竞争本就内卷的市场陷入白热化,中国云厂商深耕东南亚的意愿变强。2020年之后,上下游企业与中国云厂商抱团出海趋势明显。东软集团、用友网络等A股上市公司也在走向东南亚。 东南亚市场蛋糕…...
基于Java+SpringBoot+Vue企业OA管理系统的设计与实现 前后端分离【Java毕业设计·文档报告·代码讲解·安装调试】
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

Java架构师系统架构设计性能评估
目录 1 导论2 架构评估基础系统性能衡量的基本指标2.1 系统性能的指标2.2 数据库指标2.3 并发用户数2.4 网络延迟2.4 系统吞吐量2.5 资源性能指标3 架构评估基础服务端性能测试3.1基准测试3.2 负载测试3.3 压力测试3.4 疲劳强度测试3.5 容量测试1 导论 本章的主要内容是掌握架构…...

Android可滑动的分时图以及常用动画
先看一下效果: 自定义View 其中顶部是模仿的股票数据分时图,以前也写过详细的文章传送门,只不过不支持左右滑动,这款是在那个基础上的修改 在说一下分时图的思路吧: 可以看作是一条条相连的直线首尾相接,…...
)
软考系统架构师常考知识点整理(含案例分析、论文历年题目总结)
系统架构师常考知识点总结 计算机组成原理 1、同步/异步区分 CPU访问内存通常是同步方式 CPU与I/O接口交换信息通常是同步方式 CPU与PCI总线交换信息通常是同步方式 I/O接口与打印机交换信息则通常采用基于缓存池的异步方式, 2、双工通信方式 对端到端通信总线的信号传…...
Netty通信在中间件组件中的广泛使用-Dubbo3举例
Netty是一个高性能异步IO通信框架,封装了NIO,对各种bug做了很好的优化解决。所以很多中间件底层的通信都会使用Netty,比如说:Dubbo3,rocketmq,ElasticSearch等。 比方说,我们使用dubbo作为rpc跨…...
基于Java的在线拍卖系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技…...

Maven Pom
目录 Pom 父(Super)POM POM 标签大全详解 POM( Project Object Model,项目对象模型 ) 是 Maven 工程的基本工作单元,是一个XML文件,包含了项目的基本信息,用于描述项目如何构建,声明项目依赖…...

【运维日常】mongodb 集群生产实践
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...
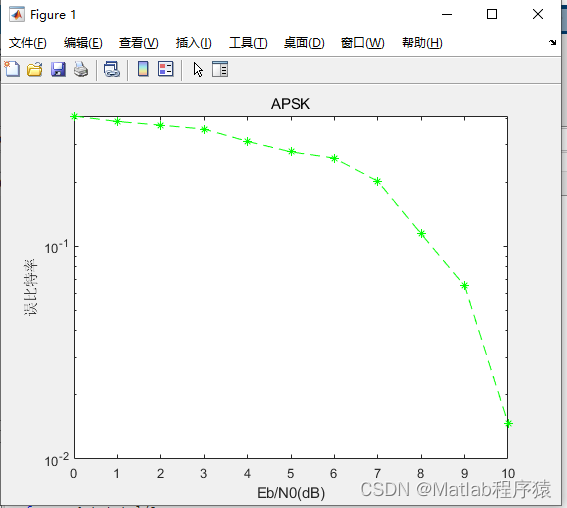
【MATLAB源码-第45期】基于matlab的16APSK调制解调仿真,使用卷积编码软判决。
操作环境: MATLAB 2022a 1、算法描述 1. 16APSK调制解调 16APSK (16-ary Amplitude Phase Shift Keying) 是一种相位调制技术,其基本思想是在恒定幅度的条件下,改变信号的相位,从而传送信息。 - 调制:在16APSK中&am…...

HarmonyOS学习路之方舟开发框架—学习ArkTS语言(状态管理 八)
其他状态管理概述 除了前面章节提到的组件状态管理和应用状态管理,ArkTS还提供了Watch和$$来为开发者提供更多功能: Watch用于监听状态变量的变化。$$运算符:给内置组件提供TS变量的引用,使得TS变量和内置组件的内部状态保持同步…...

SQL按照id集合顺序返回
SQL按照id集合顺序返回 一、需求二、SQL三、MyBatis编写四、FIELD函数五、环境 一、需求 sql这样的 SELECT id, name FROM is_parent_viewshop WHERE id IN (2350, 2396, 3768, 3718, 3692) 按照id顺序返回,sql如何写 二、SQL SELECT id, name FROM is_parent_vi…...
04训练——基于YOLO V8的自定义数据集训练——在windows环境下使用pycharm做训练-1总体步骤
在上文中,笔者介绍了使用google公司提供的免费GPU资源colab来对大量的自定义数据集进行模型训练。该方法虽然简单好用,但是存在以下几方面的短板问题: 一是需要通过虚拟服务器做为跳板机来访问,总体操作起来非常繁杂。 二是需要将大量的数据上传缓慢,管理和使用非常不友…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
